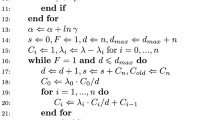Abstract
The weighted stochastic simulation algorithm (wSSA) recently developed by Kuwahara and Mura and the refined wSSA proposed by Gillespie et al. based on the importance sampling technique open the door for efficient estimation of the probability of rare events in biochemical reaction systems. In this paper, we first apply the importance sampling technique to the next reaction method (NRM) of the stochastic simulation algorithm and develop a weighted NRM (wNRM). We then develop a systematic method for selecting the values of importance sampling parameters, which can be applied to both the wSSA and the wNRM. Numerical results demonstrate that our parameter selection method can substantially improve the performance of the wSSA and the wNRM in terms of simulation efficiency and accuracy.
Similar content being viewed by others
1 Introduction
Biochemical reaction systems in living cells exhibit significant stochastic fluctuations due to a small number of molecules involved in processes such as the transcription and translation of genes [1]. A number of exact [2–7] or approximate simulation algorithms [8–19] have been developed for simulating the stochastic dynamics of such systems. Recent research shows that some rare events occurring in biochemical reaction system with an extremely small probability within a specified limited time can have profound and sometimes devastating effects [20, 21]. Hence, it is important that computational simulation and analysis of systems with critical rare events can efficiently capture such rare events. However, the existing exact simulation methods such as Gillespie's exact SSA [2, 3] often require prohibitive computation to estimate the probability of a rare events, while the approximate methods may not be able to estimate such probability accurately.
The weighted stochastic simulation algorithm (wSSA) recently developed by Kuwahara and Mura [22] based on the importance sampling technique enables one to efficiently estimate the probability of a rare event. However, the wSSA does not provide any method for selecting optimal values for importance sampling parameters. More recently, Gillespie et al. [23] analyzed the accuracy of the results yielded from the wSSA and proposed a refined wSSA that employed a try-and-test method for selecting optimal values for importance sampling parameters. It was shown that the refined wSSA could further improve the performance of wSSA. However, the try-and-test method requires some initial guessing for the sets of values from which the parameters can take. If the guessed values do not include the optimal value, then one cannot get appropriate values for the parameters. Moreover, if the number of parameters is greater than one, a very large set of values need to be guessed and tested, which may increase the likelihood of missing the optimal values and also increase computational overhead.
In this paper, we first apply the importance sampling technique to the next reaction method (NRM) of the SSA [4] and develop a weighted NRM (wNRM) as an alternative to the wSSA. We then develop a systematic method for selecting optimal values for importance sampling parameters that can be incorporated into both the wSSA and the wNRM. Our method does not need initial guess and thus can guarantee near optimal values for the parameters. Our numerical results in Section 5 demonstrate that the variance of the estimated probability of the rare event provided by the wSSA and wNRM with our parameter selection method can be more than one order magnitude lower than that provided by the wSSA or the refined wSSA for a given number of simulation runs. Moreover, the wSSA and wNRM with our parameter selection method require less simulation time than the refined wSSA for the same number of simulation runs. When this paper was under review, a method named doubly weighted SSA (dwSSA) was developed to automatically choose parameter values for the wSSA [24]. The dwSSA reduces the computational overhead required by the wSSA and the refined wSSA to select parameter values, but it produces similar variance for the estimated probability as the refined wSSA.
The remaining part of this paper is organized as follows. In Section 2, we first describe the system setup and then briefly review Gillespie's exact SSA [2, 3], the wSSA [22] and the refined wSSA [23]. In Section 3, we develop the wNRM. In Section 4, we develop a systematic method for selecting optimal values for importance sampling parameters and incorporate the parameter selection procedure into both the wSSA and the NRM. In Section 5, we give some numerical examples that illustrate the advantages of our parameter selection method. Finally in Section 6, we draw several conclusions.
2 Weighted stochastic simulation algorithms
2.1 System Description
Suppose a chemical reaction system involves a well-stirred mixture of N ≥ 1 molecular species {S1, ..., S N } that chemically interact through M ≥ 1 reaction channels {R1, ..., R M }. The dynamic state of this chemical system is described by the state vector X(t) = [X1(t), ..., X N (t)] T , where X n (t), n = 1, ..., N, is the number of S n molecules at time t, and [·] T denotes the transpose of the vector in the brackets. Following Gillespie [8], we define the dynamics of reaction R m by a state-change vector ν m = [ν1m, ..., ν Nm ] T , where ν nm gives the changes in the S n molecular population produced by one R m reaction, and a propensity function a m (x) together with the fundamental premise of stochastic chemical kinetics:

2.2 Gillespie's exact SSA
Based on the fundamental premise (1), Gillespie developed an exact SSA to simulate the occurrence of every reaction when the time evolves [3]. Specifically, Gillespie's SSA simulates the following event in each step:

It has been shown by Gillespie [2, 3] that τ and μ are two independent random variables and have the following probability density functions (PDF) and probability mass function (PMF), respectively,

and

where  . Therefore, Gillespie's direct method (DM) for the SSA generates a realization of τ and μ according to PDF (3) and PMF (4), respectively, in each step of the simulation, and then updates the system state as X(t + τ) = x + ν
μ
.
. Therefore, Gillespie's direct method (DM) for the SSA generates a realization of τ and μ according to PDF (3) and PMF (4), respectively, in each step of the simulation, and then updates the system state as X(t + τ) = x + ν
μ
.
2.3 Weighted SSA
In order to estimate the probability of a rare event that occurs with an extremely low probability in a given time period, Gillespie's SSA may require huge computation. Recently, the wSSA [22] and the refined wSSA [23] were developed to estimate the probability of a rare event with substantial reduction of computation. Following Kuwahara and Mura [22], and Gillespie et al. [23], we define the rare event E R as follows:

If we employ the SSA to estimate P(E
R
), we would have to make a large number n of simulation runs, with each starting at time 0 in state x0 and terminating either when some state x ∈ Ω is first reached or when the system time reaches T. If k is the number of those n runs that terminate for the first reason, then P(E
R
) is estimated as  . Since P(E
R
) ≪ 1, n should be very large to get a reasonably accurate estimate of P(E
R
). The wSSA employs the importance sampling technique to reduce the number of runs needed to estimate P(E
R
).
. Since P(E
R
) ≪ 1, n should be very large to get a reasonably accurate estimate of P(E
R
). The wSSA employs the importance sampling technique to reduce the number of runs needed to estimate P(E
R
).
Specifically, wSSA generates τ from its PDF (3) in the same way as used in Gillespie's DM method, but generates the reaction index μ from the following PMF:

where b
μ
(x) = γ
μ
a
μ
(x), μ = 1, ..., M,  and γ
μ
, μ = 1, ..., M are positive constants that need to be chosen carefully before simulations are run. Suppose a trajectory J generated in a simulation run contains h reactions and the i th reaction occurs at time t
i
, then the wSSA changes the PDF of the trajectory from
and γ
μ
, μ = 1, ..., M are positive constants that need to be chosen carefully before simulations are run. Suppose a trajectory J generated in a simulation run contains h reactions and the i th reaction occurs at time t
i
, then the wSSA changes the PDF of the trajectory from  to
to  , where t0 = 0. By choosing appropriate γ
μ
, μ = 1, ..., M, one can increase the probability of the trajectories that lead to the rare event. If k trajectories out of n simulation runs lead to the rare event, then the importance sampling technique tells us that an unbiased estimate of P(E
R
) is given by
, where t0 = 0. By choosing appropriate γ
μ
, μ = 1, ..., M, one can increase the probability of the trajectories that lead to the rare event. If k trajectories out of n simulation runs lead to the rare event, then the importance sampling technique tells us that an unbiased estimate of P(E
R
) is given by

where j and i are indices of the trajectories and reactions in a trajectory, respectively,  , and
, and

which can be obtained in each simulation step.
Kuwahara and Mura [22] did not provide any method for choosing γ
μ
, although their numerical results with some pre-specified γ
μ
for several reaction systems demonstrated that the wSSA could reduce computation substantially. Gillespie et al. [23] analyzed the variance of  obtained from the wSSA and refined the wSSA by proposing a try-and-test method for choosing γ
μ
. In the try-and-test method, several sets of values are pre-specified for γ
μ
, μ = 1, ..., M. A relatively small number of simulation runs of the standard SSA are made for each set of the values to obtain an estimate of the variance of
obtained from the wSSA and refined the wSSA by proposing a try-and-test method for choosing γ
μ
. In the try-and-test method, several sets of values are pre-specified for γ
μ
, μ = 1, ..., M. A relatively small number of simulation runs of the standard SSA are made for each set of the values to obtain an estimate of the variance of  , and then the set of values that yielded the smallest variance is chosen. Although the try-and-test method provides a way of choosing γ
μ
, it requires some guessing to get several sets of pre-specified values for all γ
μ
and also some computational overhead to estimate the variance of
, and then the set of values that yielded the smallest variance is chosen. Although the try-and-test method provides a way of choosing γ
μ
, it requires some guessing to get several sets of pre-specified values for all γ
μ
and also some computational overhead to estimate the variance of  for each set of values. More recently, the dwSSA was developed in [24] to automatically choose parameter values for the wSSA by applying the cross-entropy method originally proposed in [25] for optimizing the importance sampling method.
for each set of values. More recently, the dwSSA was developed in [24] to automatically choose parameter values for the wSSA by applying the cross-entropy method originally proposed in [25] for optimizing the importance sampling method.
3 Weighted NRM
The wSSA is based on the DM for the SSA, which needs to generate two random variables in each simulation step. However, the NRM of Gibson and Bruck [4] requires only one random variable in each simulation step. In this section, we apply the importance sampling technique to the NRM and develop the wNRM.
The key to making the wSSA more efficient than the standard SSA is to change the probability of each reaction appropriately but without changing the distribution of the time τ between any two consecutive reactions. Since the NRM determines the reaction occurring in a simulation step by choosing the reaction that requires the smallest waiting time, it seems difficult to change the probability of each reaction without changing the distribution of τ. However, we notice that the PDF of τ in (3) only depends on a0(x) not individual a μ (x). Hence, we can change the probability of each reaction by changing the corresponding propensity function but without changing the distribution of τ, so long as we keep the sum of the propensity functions equal to a0(x). To this end, we define

where b
m
(x) = γ
m
a
m
(x) is defined in the same way as in the wSSA. It is easy to verify that  . If we generate τ
m
from an exponential distribution p(τ
m
) = d
m
(x) exp(-d
m
(x)τ
m
), τ
m
> 0, as the waiting time of reaction channel m, and choose μ = arg
m
min{τ
m
, m = 1, ..., M} as the index of the channel that fires, then it can be easily shown that the PDF of τ = min{τ
m
, m = 1, ..., M} follows the exponential distribution in (3) and that the probability of reaction μ is q
μ
= d
μ
(x)/d0(x) = b
μ
(x)/b0(x). If we repeat this procedure in each simulation step, we would have modified the first reaction method (FRM) [3] for the standard SSA and got a weighted FRM (wFRM). Clearly, the wFRM is not efficient since it generates M random variables in each step. However, following Gibson and Bruck [4], we can convert the wFRM into a more efficient wNRM by reusing τ
m
s.
. If we generate τ
m
from an exponential distribution p(τ
m
) = d
m
(x) exp(-d
m
(x)τ
m
), τ
m
> 0, as the waiting time of reaction channel m, and choose μ = arg
m
min{τ
m
, m = 1, ..., M} as the index of the channel that fires, then it can be easily shown that the PDF of τ = min{τ
m
, m = 1, ..., M} follows the exponential distribution in (3) and that the probability of reaction μ is q
μ
= d
μ
(x)/d0(x) = b
μ
(x)/b0(x). If we repeat this procedure in each simulation step, we would have modified the first reaction method (FRM) [3] for the standard SSA and got a weighted FRM (wFRM). Clearly, the wFRM is not efficient since it generates M random variables in each step. However, following Gibson and Bruck [4], we can convert the wFRM into a more efficient wNRM by reusing τ
m
s.
In the FRM, we used τ
m
to denote the putative waiting or relative time for the m th reaction channel to fire. Following Gibson and Bruck [4], we will use τ
m
to denote the putative absolute time when the m th reaction channel will fire. Suppose that the μ th reaction channel fires at time t in the current step. After updating the state vector and propensity functions, we calculate new d
m
(x), m = 1, ..., M, which we denote as  . Then, we generate a random variable
. Then, we generate a random variable  from an exponential distribution with parameter
from an exponential distribution with parameter  and set
and set  . For other channels with an index m ≠ μ, we update τ
m
as follows:
. For other channels with an index m ≠ μ, we update τ
m
as follows:

Following Gibson and Bruck [4], we can show that the new τ
m
-t, m = 1, ..., M, are independent exponential random variables with parameters  , m = 1, ..., M, respectively. Therefore, in the next step, we can choose μ = arg
m
min{τ
m
, m = 1, ..., M} as the index of the channel that fires as done in NRM, update t as t = τ
μ
, and then repeat the process just described. Clearly, the wNRM only needs to generate one random variable in each step. We can further improve the efficiency of the wNRM by using the dependency graph
, m = 1, ..., M, respectively. Therefore, in the next step, we can choose μ = arg
m
min{τ
m
, m = 1, ..., M} as the index of the channel that fires as done in NRM, update t as t = τ
μ
, and then repeat the process just described. Clearly, the wNRM only needs to generate one random variable in each step. We can further improve the efficiency of the wNRM by using the dependency graph  and the indexed priority queue
and the indexed priority queue  defined by Gibson and Bruck [4]. The dependency graph
defined by Gibson and Bruck [4]. The dependency graph  tells precisely which propensity functions need to be updated after a reaction occurs. The indexed priority queue
tells precisely which propensity functions need to be updated after a reaction occurs. The indexed priority queue  can be exploited to find the minimum τ
m
and the reaction index in each step more efficiently than finding the reaction index from the PMF (4) directly as done in the DM. However, some computational overhead is needed to maintain the data structure of
can be exploited to find the minimum τ
m
and the reaction index in each step more efficiently than finding the reaction index from the PMF (4) directly as done in the DM. However, some computational overhead is needed to maintain the data structure of  .
.
Essentially, our wNRM runs simulation in the same way as the NRM except that the wNM generates τ
m
using a parameter d
m
(x) instead of a
m
(x). To estimate the probability of the rare event  , we calculate a weight
, we calculate a weight  in each step and get
in each step and get  using (7). The wNRM is summarized in the following algorithm:
using (7). The wNRM is summarized in the following algorithm:
Algorithm 1 (wNRM)
1. k1 ← 0, k2 ← 0, set values for all γ
m
; generate a dependency graph .
.
2. for i = 1 to n, do
3. t ← 0, x ← x0, w ← 1.
4. evaluate a m (x) and b m (x) for all m; calculate all d m (x).
5. for each m, generate a unit-interval uniform random variable r m ; τ m = ln(1/r m )/d m (x).
6. store τ
m
in an indexed priority queue .
.
7. while t ≤ T, do
8. if x ∈ Ω, then
9. k1 ← k1 + w, k2 ← k2 + w2
10. break out the while loop
11. end if
12. find μ = arg
m
min{τ
m
, m = 1, ..., M} and τ = min{τ
m
, m = 1, ..., M} from .
.
13. w ← w × a μ (x)/d μ (x).
14. x ← x + ν μ , t ← τ.
15. Find a
m
(x) need to be updated from ; evaluate these a
m
(x) and the corresponding b
m
(x); calculate all
; evaluate these a
m
(x) and the corresponding b
m
(x); calculate all .
.
16. for all m ≠ μ,  ; generate a unit-interval uniform random variable r
μ
;
; generate a unit-interval uniform random variable r
μ
;  ; update
; update .
.
17.  .
.
18. end while
19. end for
20.

21. calculate , with a 68% uncertainty of
, with a 68% uncertainty of .
.
Note that Gibson and Bruck [4] argued that the NRM is more efficient than the DM of Gillespie's SSA for the loosely coupled chemical reaction systems. On the other hand, Cao et al. [5] optimized the DM and argued that the optimized DM is more efficient for most practical reaction systems. Regardless of the debate about the efficiency, here we propose the wNRM as an alternative of the wSSA which is based on the DM. While our simulation results in Section 5 demonstrate that the wNRM is more efficient than the refined wSSA for the three reaction systems tested, the wSSA may be more efficient in simulating some other systems.
As in the wSSA, Algorithm 1 does not provide a method for selecting the values of parameters γ m , m = 1, ..., M. Although we could incorporate the try-and-test method in refined wSSA into Algorithm 1, we will develop a more systematic method for selecting parameters in the next section. This parameter selection method will be applicable to both the wSSA and the wNRM and can significantly improve the performance of both algorithms as will be demonstrated in Section 5.
4 Parameter selection for wSSA and wNRM
Let us denote the set of all possible state trajectories in the time interval [0 T] as  and the set of trajectories that first reach any state in Ω during [0 T] as
and the set of trajectories that first reach any state in Ω during [0 T] as  . Let the probability of a trajectory J be P
J
. Then, we have
. Let the probability of a trajectory J be P
J
. Then, we have  , where the indicator function
, where the indicator function  if
if  or 0 if
or 0 if  . Importance sampling used in the wSSA and the wNRM arises from the factor that we can write P(E
R
) as
. Importance sampling used in the wSSA and the wNRM arises from the factor that we can write P(E
R
) as

where Q
J
is the probability used in simulation to generate trajectory J, which is different from the true probability P
J
if the original system evolves naturally. If we make n simulation runs with altered trajectory probabilities, (11) implies that we can estimate P(E
R
) as  which is essentially (7). The variance of
which is essentially (7). The variance of  depends on Q
J
s. Appropriate Q
J
s yield small variance, thereby improving the accuracy of the estimate or equivalently reducing the number of runs for a given variance. The "rule of thumb" [23, 26–28] for choosing good Q
J
s is that Q
J
should be roughly proportional to
depends on Q
J
s. Appropriate Q
J
s yield small variance, thereby improving the accuracy of the estimate or equivalently reducing the number of runs for a given variance. The "rule of thumb" [23, 26–28] for choosing good Q
J
s is that Q
J
should be roughly proportional to  . However, at least two difficulties arise if we apply the rule of thumb based on (11). First, the number of all possible trajectories is very large and we do not know the trajectories that lead to the rare event and their probabilities. Second, since we can only adjust the probability of each reaction in each step, it is not clear how this adjustment can affect the probability of a trajectory. To overcome these difficulties, we next use an alternative expression for P(E
R
) based on which we apply the importance sampling technique.
. However, at least two difficulties arise if we apply the rule of thumb based on (11). First, the number of all possible trajectories is very large and we do not know the trajectories that lead to the rare event and their probabilities. Second, since we can only adjust the probability of each reaction in each step, it is not clear how this adjustment can affect the probability of a trajectory. To overcome these difficulties, we next use an alternative expression for P(E
R
) based on which we apply the importance sampling technique.
Let us denote the number of reactions occurring in the time interval [0 t] as K
t
and the maximum value of K
T
as  . Let E
K
be the rare event occurring at the K th
. Let E
K
be the rare event occurring at the K th  reaction at any t ≤ T, and P(E
K
) be the probability of E
K
in the original system that evolve naturally with the original probability rate constants. Then, we have
reaction at any t ≤ T, and P(E
K
) be the probability of E
K
in the original system that evolve naturally with the original probability rate constants. Then, we have

If Q(E
K
) is the probability of event E
K
in the weighted system that evolves with adjusted probability rate constants, the rule of thumb for choosing good Q(E
K
) is that we should make Q(E
K
) approximately proportional to P(E
K
). However, it is still difficult to apply the rule of thumb, because it is difficult to control every Q(E
K
) simultaneously. Hence, we relax the rule of thumb and will maximize the Q(E
K
) corresponding to the maximum P(E
K
) or the one near maximum if the exact maximum P(E
K
) cannot be determined precisely. The rationale of this heuristic rule is based on the following argument. If  is the maximum one among all
is the maximum one among all  , the sum of
, the sum of  and its closely related terms, such as
and its closely related terms, such as  ,
,  ,
,  and
and  , very likely dominates the sum in the right-hand side of (12). Maximizing
, very likely dominates the sum in the right-hand side of (12). Maximizing  not only proportionally increases
not only proportionally increases  , and its closely related terms, such as
, and its closely related terms, such as  ,
,  ,
,  and
and  , but also significantly increases the probability of the occurrence of the rare event. Note that a similar heuristic rule relying on the event with maximum probability was proposed in [29] for estimating the probability of rare events in highly reliable Markovian systems.
, but also significantly increases the probability of the occurrence of the rare event. Note that a similar heuristic rule relying on the event with maximum probability was proposed in [29] for estimating the probability of rare events in highly reliable Markovian systems.
Before proceeding with our derivations, we need to specify Ω. In the rest of the paper, we assume that Ω contains one single state X defined as X i = X i (0) + η, where η is a constant and i ∈ {1, 2, ..., N}. Let us denote the number of firings of the m th reaction channel in the trajectory leading to the rare event as K m . Then, we have

We first divide all reactions into three groups using the following general rule: G1 group consists of reactions with ν im η > 0, G2 group consists of reactions with ν im η < 0, and G3 group consists of reactions with ν im = 0. The rationale for the partition rule is that the reactions in G1 (G2) group increase (decrease) the probability of the rare event and that the reactions in G3 group do not affect X i (t) directly. We further refine the partition rule as follows. If a reaction R m is in the G1 group based on the general rule but a m (x) = 0 whenever one R m reaction occurs, we move R m into the G3 group. Similarly, if a reaction R m is in the G2 group based on the general rule but a m (x) = 0 whenever one R m reaction occurs, we move R m into the G3 group. For most cases, we only need the general partition rule. The refining rule described here is to deal with the situation where one or several X i (t)s always take values 1 or 0 as in the system considered in Section 5.3. More refining rules may be added following the rationale just described, after we see more real-world reaction systems.
We typically only need to consider elementary reactions including bimolecular and monomolecular reactions [30]. Hence, the possible values for all ν
im
are 0, ±1, ±2. For the simplicity of derivations, we now only consider the case where ν
im
= 0, ±1, i.e., we assume that the system does not have any bimolecular reactions with two identical reactant molecules or dimerization reactions. We will later generalize our method to the system with dimerization reactions. Let us define  ,
,  and
and  , then (13) becomes
, then (13) becomes

Let us denote  as the expected value of K
t
. Since the number of reactions occurring in any small time interval is approximately a Poisson random variable [8], K
t
is the sum of a large number of independent Poisson random variables when t is relatively large. Then, by the central limit theorem, K
t
can be approximated as a Gaussian random variable with mean
as the expected value of K
t
. Since the number of reactions occurring in any small time interval is approximately a Poisson random variable [8], K
t
is the sum of a large number of independent Poisson random variables when t is relatively large. Then, by the central limit theorem, K
t
can be approximated as a Gaussian random variable with mean  . Indeed, in all chemical reaction systems [6, 19, 31] we tested so far, we observed that Kt follows a unimodal distribution with a peak at
. Indeed, in all chemical reaction systems [6, 19, 31] we tested so far, we observed that Kt follows a unimodal distribution with a peak at  and its standard deviation is small relative to
and its standard deviation is small relative to  . Since the mean first passage time of the rare event is much larger than T[23], the rare event most likely occurs at a time near T. Based on these two observations, we argue that
. Since the mean first passage time of the rare event is much larger than T[23], the rare event most likely occurs at a time near T. Based on these two observations, we argue that  for all
for all  . Therefore, we should have
. Therefore, we should have  . When
. When  occurs, we have
occurs, we have

Since both (14) and (15) need to be satisfied in order for the event  to occur and since
to occur and since  ,
,  and
and  , we get the second requirement for K
E
: K
E
≥ |η|. Combining the two requirements on K
E
, we obtain
, we get the second requirement for K
E
: K
E
≥ |η|. Combining the two requirements on K
E
, we obtain  .
.
The probability P(E
K
) can be expressed as  . Since P(X(t) ∈ Ω|K
t
= K) is determined by the constant K, it is independent of t. Hence, we have
. Since P(X(t) ∈ Ω|K
t
= K) is determined by the constant K, it is independent of t. Hence, we have  . Due to the unimodal distribution of K
t
we mentioned earlier, we have
. Due to the unimodal distribution of K
t
we mentioned earlier, we have  for those
for those  ;
;  for those K close to
for those K close to  ; and
; and  quickly decreases to zero when K increases beyond
quickly decreases to zero when K increases beyond  . In other words,
. In other words,  is approximately a constant for
is approximately a constant for  and quickly decreases to zero when
and quickly decreases to zero when  . Now let us consider event E
K
with K = |η| in the case
. Now let us consider event E
K
with K = |η| in the case  . In this case, P (X(t) ∈ Ω|K
t
= K) is very small because this is an extreme case where
. In this case, P (X(t) ∈ Ω|K
t
= K) is very small because this is an extreme case where  and
and  if η > 0 or
if η > 0 or  and
and  if η < 0. Therefore, we can increase P(E
K
) if we increase K, but we do not want to increase K too much because as we discussed
if η < 0. Therefore, we can increase P(E
K
) if we increase K, but we do not want to increase K too much because as we discussed  decreases quickly when K increases in the case
decreases quickly when K increases in the case  . Consequently, we suggest that we choose
. Consequently, we suggest that we choose  , where
, where  is the standard deviation of K
T
which can be estimated by making hundreds of runs of the standard SSA. In case
is the standard deviation of K
T
which can be estimated by making hundreds of runs of the standard SSA. In case  , we choose
, we choose  based on the same argument that
based on the same argument that  decreases quickly if we further increase K
E
.
decreases quickly if we further increase K
E
.
Applying the relaxed rule of thumb, we need to adjust probability rate constants in simulation to maximize  . Since we do not change the distribution of τ, we do not change the distribution of K
T
and thus
. Since we do not change the distribution of τ, we do not change the distribution of K
T
and thus  . Hence, maximizing Q(E
K
) is equivalent to maximizing Q(X(t) ∈ Ω|K
t
= K
E
). Now we are in a position to summarize our strategy of applying the important sampling technique in simulation as follows: we will choose probability parameters to maximize Q(X(t) ∈ Ω|K
t
= K
E
), where
. Hence, maximizing Q(E
K
) is equivalent to maximizing Q(X(t) ∈ Ω|K
t
= K
E
). Now we are in a position to summarize our strategy of applying the important sampling technique in simulation as follows: we will choose probability parameters to maximize Q(X(t) ∈ Ω|K
t
= K
E
), where

We next consider systems with only G1 and G2 reaction groups and then consider more general systems with all three reaction groups.
4.1 Systems with G1and G2reaction groups
Since we do not have G3 group, (15) becomes

Combining (14) and (17), we get  and
and  if the final state after the last reaction occurs is in Ω. The last reaction should be a reaction from G1 group. Otherwise, the state already reached Ω before the last reaction occurs. Suppose that in simulation the total probability of the occurrence of reactions in G1 group is a constant
if the final state after the last reaction occurs is in Ω. The last reaction should be a reaction from G1 group. Otherwise, the state already reached Ω before the last reaction occurs. Suppose that in simulation the total probability of the occurrence of reactions in G1 group is a constant  and then the total probability of the occurrence of reactions in G2 group is
and then the total probability of the occurrence of reactions in G2 group is  . Then, Q(X(t) ∈ Ω|K
t
= K
E
) can be found from a binomial distribution as follows
. Then, Q(X(t) ∈ Ω|K
t
= K
E
) can be found from a binomial distribution as follows

where  and
and  as determined earlier. Setting the derivative of Q(X(t) ∈ Ω|K
t
= K
E
) with respect to
as determined earlier. Setting the derivative of Q(X(t) ∈ Ω|K
t
= K
E
) with respect to  to be zero, we get
to be zero, we get  and
and  that maximize Q(X(t) ∈ Ω|K
t
= K
E
) as follows:
that maximize Q(X(t) ∈ Ω|K
t
= K
E
) as follows:

To ensure that reactions in G1 (G2) group occur with probability  in each step of simulation, we adjust the probability of each reaction as follows
in each step of simulation, we adjust the probability of each reaction as follows

where  and
and  . It is easy to verify that
. It is easy to verify that  and
and  . As defined in (8), the weight for estimating the probability of the rare event is w
μ
= p
μ
/q
μ
if the μ th reaction channel fires.
. As defined in (8), the weight for estimating the probability of the rare event is w
μ
= p
μ
/q
μ
if the μ th reaction channel fires.
4.2 Systems with G1, G2and G3reaction groups
Combining (14) and (15), we get  and
and  . Since
. Since  , we have
, we have  . Suppose that in simulation the total probabilities of the occurrence of reactions in G1, G2 and G3 are constants
. Suppose that in simulation the total probabilities of the occurrence of reactions in G1, G2 and G3 are constants  ,
,  and
and  , respectively. Then, Q(X(t) ∈ Ω|K
t
= K
E
) can be found from a multinomial distribution as follows
, respectively. Then, Q(X(t) ∈ Ω|K
t
= K
E
) can be found from a multinomial distribution as follows

where  and
and  as determined earlier. Since there are (K
E
- η)/2 + 1 terms of the sum in (21), it is difficult to find
as determined earlier. Since there are (K
E
- η)/2 + 1 terms of the sum in (21), it is difficult to find  ,
,  and
and  that maximize Q(X(t) ∈ Ω|K
t
= K
E
). So we will use a different approach to find
that maximize Q(X(t) ∈ Ω|K
t
= K
E
). So we will use a different approach to find  ,
,  and
and  as described in the following.
as described in the following.
Let  ,
,  and
and  be the average number of reactions of G1, G2 and G3 groups that occur in the time interval [0 T] in the original system. Since we have
be the average number of reactions of G1, G2 and G3 groups that occur in the time interval [0 T] in the original system. Since we have  , we define
, we define  ,
,  , and
, and  . Then, we can approximate P(X(t) ∈ Ω|K
t
= K
E
) in the original system, which is the counter part of Q(X(t) ∈ Ω|K
t
= K
E
) in the weighted system, using the right-hand side of (21) but with
. Then, we can approximate P(X(t) ∈ Ω|K
t
= K
E
) in the original system, which is the counter part of Q(X(t) ∈ Ω|K
t
= K
E
) in the weighted system, using the right-hand side of (21) but with  , i = 1, 2, 3, replaced by
, i = 1, 2, 3, replaced by  i = 1, 2, 3, respectively. This gives
i = 1, 2, 3, respectively. This gives

Suppose that the (κ + 1)th term of the sum in (22) is the largest. We further relax the rule of thumb and maximize the (κ + 1)th term of the sum in (21) to find  ,
,  and
and  .
.
It is not difficult to find the (κ + 1)th term of the sum in (22). Let us denote the  term of the sum in (22) as
term of the sum in (22) as  . We can exhaustively search over all
. We can exhaustively search over all  ,
,  to find κ. However, this may require relatively large computation because the factorials involved in
to find κ. However, this may require relatively large computation because the factorials involved in  . We can reduce computation by searching over
. We can reduce computation by searching over  ,
,  , which are given by
, which are given by

Specifically, we calculate all  from (23). If
from (23). If  but
but  , then
, then  is a local maximum. After obtaining all local maximums, we can find the global maximum f(κ) from the local maximums.
is a local maximum. After obtaining all local maximums, we can find the global maximum f(κ) from the local maximums.
After we find κ, we set the partial derivatives of the (κ + 1)th term of the sum in (21) with respect to  and
and  to be zero. This gives the following optimal
to be zero. This gives the following optimal  ,
,  and
and 

Substituting  and
and  in (24) into (20), we get the probability q
m
, m ∈ G1 or G2 that is used to generate the m th reaction in each step of simulation. For G3 group, we get the probability of each reaction as follows
in (24) into (20), we get the probability q
m
, m ∈ G1 or G2 that is used to generate the m th reaction in each step of simulation. For G3 group, we get the probability of each reaction as follows

where  .
.
While we can use q
m
in (25) to generate reactions in G3 group, we next develop an optional method for fine-tuning q
m
, m ∈ G3, which can further reduce the variance of  . We divide G3 group into three subgroups: G31, G32 and G33. Occurrence of reactions in G31 group increases the probability of occurrence of reactions in
. We divide G3 group into three subgroups: G31, G32 and G33. Occurrence of reactions in G31 group increases the probability of occurrence of reactions in  group or reduces the probability of the occurrence of the reactions in
group or reduces the probability of the occurrence of the reactions in  group, which in turn increases the probability of the rare event. Occurrence of reactions in G32 group reduces the probability of occurrence of reactions in
group, which in turn increases the probability of the rare event. Occurrence of reactions in G32 group reduces the probability of occurrence of reactions in  group or increases he probability of the occurrence of reactions in
group or increases he probability of the occurrence of reactions in  group, which reduces the probability of the are event. Occurrence of reactions in G33 group does not change the probability of occurrence of reactions in
group, which reduces the probability of the are event. Occurrence of reactions in G33 group does not change the probability of occurrence of reactions in  and
and  groups, which does not change the probability of the rare event.
groups, which does not change the probability of the rare event.
Let  ,
,  and
and  be the average number of reactions from G31, G32 and G33 that occur in the time interval [0 T] in the original system. we define
be the average number of reactions from G31, G32 and G33 that occur in the time interval [0 T] in the original system. we define  ,
,  and
and  . Our goal is to make Q31 to be greater than
. Our goal is to make Q31 to be greater than  and Q32 to be less than
and Q32 to be less than  to increase the probability of the rare event. However, this may not feasible when
to increase the probability of the rare event. However, this may not feasible when  . Hence, we can fine-tune
. Hence, we can fine-tune  ,
,  and
and  only when
only when  and propose the following formula to determine Q31, Q32 and Q33:
and propose the following formula to determine Q31, Q32 and Q33:

where α, β ∈ (0 1) are two pre-specified constants. It is not difficult to verify from (26) that  . To ensure that
. To ensure that  and
and  , we choose α and β satisfying 0 ≤ β < 1 and
, we choose α and β satisfying 0 ≤ β < 1 and  .
.
Finally, we obtain q m for m ∈ G3 as follows

where  , i = 1, 2, 3.
, i = 1, 2, 3.
4.3 Systems with dimerization reactions
So far we assumed that the system did not have any dimerization reactions, i.e. the system consisted of reactions with |ν im | = 0 or 1. We now generalize our methods developed earlier to the system with dimerization reactions. If there are dimerization reactions in G1 and G2 groups, we further divide G1 group into G11 and G12 subgroups and G2 group into G21 and G22 subgroups. The G11 group contains reactions with ν im sign(η) = 1, where sign(η) = 1 when η > 0 and sign(η) = -1 when η < 0. The G12 group contains reactions with ν im sign(η) = 2. The G21 group contains reactions with ν im sign(η) = -1, while the G12 group contains reactions with ν im sign(η) = -2.
Let us define  ,
,  ,
,  and
and  . Clearly, we have
. Clearly, we have  and
and  . Then, (13) becomes
. Then, (13) becomes

Let us consider systems with G1 and G2 groups but without G3 group. Although we still have  or equivalently
or equivalently  , we cannot obtain four unknowns
, we cannot obtain four unknowns  ,
,  ,
,  and
and  from only two equations.
from only two equations.
Suppose that  ,
,  ,
,  and
and  are average number of reactions from G11, G12, G21 and G22 groups that occur in the time interval [0 T] in the original system. We notice from (20) that we do not change the ratio of the probabilities of two reactions in the same group, i.e.,
are average number of reactions from G11, G12, G21 and G22 groups that occur in the time interval [0 T] in the original system. We notice from (20) that we do not change the ratio of the probabilities of two reactions in the same group, i.e.,  if m1 and m2 are in the same G1 or G2 group. Therefore, we would expect that
if m1 and m2 are in the same G1 or G2 group. Therefore, we would expect that  and
and  . Using these two relationships, we can write (28) as
. Using these two relationships, we can write (28) as

where  and
and  .
.
From (17) and (29), we obtain  and
and  . Substituting
. Substituting  and
and  into (18) and maximizing Q(X(t) ∈ Ω|K
t
= K
E
), we obtain
into (18) and maximizing Q(X(t) ∈ Ω|K
t
= K
E
), we obtain

We then substitute  and
and  into (20) to get q
m
.
into (20) to get q
m
.
Now let us consider the systems with G1, G2 and G3 reactions. From (29), we have  , and from (15) and (29), we obtain
, and from (15) and (29), we obtain  . Since
. Since  , we have
, we have  . Following the derivations in Section 4.2, we can get q
m
for any reaction. More specifically, substituting
. Following the derivations in Section 4.2, we can get q
m
for any reaction. More specifically, substituting  ,
,  and the upper limit of
and the upper limit of  into (21), we obtain Q(X(t) ∈ Ω|K
t
= K
E
). We can also get P(X(t) ∈ Ω|K
t
= K
E
) similar to (22) by replacing
into (21), we obtain Q(X(t) ∈ Ω|K
t
= K
E
). We can also get P(X(t) ∈ Ω|K
t
= K
E
) similar to (22) by replacing  in Q(X(t) ∈ Ω|K
t
= K
E
) with
in Q(X(t) ∈ Ω|K
t
= K
E
) with  . Then, we determine the maximum term of the sum in P(X(t) ∈ Ω|K
t
= K
E
) and denote the value of
. Then, we determine the maximum term of the sum in P(X(t) ∈ Ω|K
t
= K
E
) and denote the value of  corresponding to the maximum term as κ + 1. We find
corresponding to the maximum term as κ + 1. We find  ,
,  and
and  by maximizing the (κ + 1)th term of the sum in Q(X(t) ∈ Ω|K
t
= K
E
). Finally, we substitute
by maximizing the (κ + 1)th term of the sum in Q(X(t) ∈ Ω|K
t
= K
E
). Finally, we substitute  and
and  into (20) to get q
m
, m ∈ G1 or G2. For the reactions in G3 group, we can either substitute
into (20) to get q
m
, m ∈ G1 or G2. For the reactions in G3 group, we can either substitute  into (25) to obtain q
m
, or if we want to fine-tune q
m
, we use (26) and (27) to get q
m
.
into (25) to obtain q
m
, or if we want to fine-tune q
m
, we use (26) and (27) to get q
m
.
4.4 wSSA and wNRM with parameter selection
The key to determining probability of each reaction q
m
is to find the total probability of each group,  ,
,  ,
,  ,
,  ,
,  and
and  . This requires the average number of reactions of each group occurring during the interval [0 T] in the original system,
. This requires the average number of reactions of each group occurring during the interval [0 T] in the original system,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . If the system is relatively simple, we may get these numbers analytically. If we cannot obtain them analytically, we can estimate them by running Gillespie's exact SSA. Since the number of runs needed to estimates these numbers is much smaller than the number of runs needed to estimate the probability of the rare event, the computational overhead is negligible.
. If the system is relatively simple, we may get these numbers analytically. If we cannot obtain them analytically, we can estimate them by running Gillespie's exact SSA. Since the number of runs needed to estimates these numbers is much smaller than the number of runs needed to estimate the probability of the rare event, the computational overhead is negligible.
We next summarize the wSSA incorporating the parameter selection method in the following algorithm. We will not include the procedure for fine-tuning the probability rate constants of reactions in the G3 group, but will describe how to add this optional procedure to the algorithm. We will also describe how to modify Algorithm 1 to incorporate the parameter selection procedure into the wNRM.
Algorithm 2 (wSSA with parameter selection)
1. run Gillespie's exact SSA 103-104times to get estimates of ,
,  ,
,  ,
,  ,
,  , and
, and ; determine K
E
from (16).
; determine K
E
from (16).
2. if the system has only G1and G2reactions, calculate and
and from (19) if there is no dimerization reaction or from (30) if there are dimerization reaction(s), if the system has G1, G2and G3reactions, calculate
from (19) if there is no dimerization reaction or from (30) if there are dimerization reaction(s), if the system has G1, G2and G3reactions, calculate ,
,  and
and from (24).
from (24).
3. k1 ← 0, k2 ← 0.
4. for i = 1 to n, do
5. t ← 0, x ← x0, w ← 1.
6. while t ≤ T, do
7. if x ∈ Ω, then
8. k1 ← k1 + w, k2 ← k2 + w2
9. break out the while loop
10. end if
11. evaluate all a m (x); calculate a0(x).
12. generate two unit-interval uniform random variables r1and r2.
13. τ ← ln(1/r)1)/a0(x)
14. calculate all q m from (20) and (25).
15. μ ← smallest integer satisfying .
.
16. w ← w × (a μ (x)/a0(x))/(q μ (x)/q0(x)).
17. x ← x + ν μ , t ← t + τ.
18. end while
19. end for
20.

21. estimate , with a 68% uncertainty of
, with a 68% uncertainty of .
.
If  and we want to fine-tune the probability rate constants of the reactions in the G3 group, we modify Algorithm 2 as follows. In step 1, we also estimate
and we want to fine-tune the probability rate constants of the reactions in the G3 group, we modify Algorithm 2 as follows. In step 1, we also estimate  ,
,  and
and  and choose the value of α and β in (26). In step 2, we also calculate
and choose the value of α and β in (26). In step 2, we also calculate  ,
,  and
and  from (26). In step 14, we calculate q
m
for G3 reactions from (27) instead of (25). Comparing with the refined wSSA [23], the wSSA with our parameter selection procedure does not need to make some guessing about the parameters for adjusting the probability of each reaction q
m
, but directly calculate q
m
using a systematically developed method. This has two main advantages. First, our method will always adjust q
m
appropriately to reduce the variance of
from (26). In step 14, we calculate q
m
for G3 reactions from (27) instead of (25). Comparing with the refined wSSA [23], the wSSA with our parameter selection procedure does not need to make some guessing about the parameters for adjusting the probability of each reaction q
m
, but directly calculate q
m
using a systematically developed method. This has two main advantages. First, our method will always adjust q
m
appropriately to reduce the variance of  , whereas the refined wSSA may not adjust q
m
as well as our method, especially if the initial guessed values are far away from the optimal values. Second, as we mentioned earlier, the computational overhead of our method is negligible, whereas the refined wSSA requires non-negligible computational overhead for determining parameters. Indeed, as we will show in Section 5, the variance of
, whereas the refined wSSA may not adjust q
m
as well as our method, especially if the initial guessed values are far away from the optimal values. Second, as we mentioned earlier, the computational overhead of our method is negligible, whereas the refined wSSA requires non-negligible computational overhead for determining parameters. Indeed, as we will show in Section 5, the variance of  provided by the wSSA with our parameter selection method can be more than one order of magnitude lower than that provided by the refined wSSA for given number of n. Moreover, the wSSA with our parameter selection method is faster than the refined wSSA, since it requires less computational overhead to adjust q
m
.
provided by the wSSA with our parameter selection method can be more than one order of magnitude lower than that provided by the refined wSSA for given number of n. Moreover, the wSSA with our parameter selection method is faster than the refined wSSA, since it requires less computational overhead to adjust q
m
.
We can also incorporate our parameter selection method without the fine-tuning procedure into the wNRM as follows. We replace the first step of Algorithm 1 with the first three steps of Algorithm 2. We then modify the fourth step of Algorithm 1 as follows: evaluate all a
m
(x), calculate all q
m
from (20) and (25), and calculate all d
m
(x) as d
m
(x) = q
m
a0(x). Finally, we change the fifth step of Algorithm 1 to the following: find a
m
(x) need to be updated from  and evaluate these a
m
(x); calculate all q
m
from (20) and (25), and calculate all
and evaluate these a
m
(x); calculate all q
m
from (20) and (25), and calculate all  as
as  . We can also fine-tune the probability rate constants of G3 reactions in the wNRM in the same way as described in the previous paragraph for the wSSA. Note that since our parameter selection method employs a systematic method for partitioning reactions into three groups as discussed earlier, our method can be applied to any real chemical reaction systems.
. We can also fine-tune the probability rate constants of G3 reactions in the wNRM in the same way as described in the previous paragraph for the wSSA. Note that since our parameter selection method employs a systematic method for partitioning reactions into three groups as discussed earlier, our method can be applied to any real chemical reaction systems.
5 Numerical examples
In this section, we present simulation results for several chemical reaction systems to demonstrate the accuracy and efficiency of the wSSA and wNRM with our parameter selection method, which we refer to as wSSAps and wNRMps, respectively, in the rest of the paper. All simulations were run in Matlab on a PC with an Intel dual Core 2.67-GHz CPU and 3G-byte memory running Windows XP.
5.1 Single species production-degradation model
This simple system was originally used by Kuwahara and Mura [22] and then Gillespie et al. [23] to test the wSSA and the refined wSSA. It includes the following two chemical reactions:

In reaction R1, species S1 synthesizes species S2 with a probability rate constant c1, while in reaction R2, species S2 is degraded with a probability rate constant c2. We used the same initial state and probability rate constants as used in [22, 23]: X1(0) = 1, X2(0) = 40, c1 = 1 and c2 = 0.025.
It is observed that the system is at equilibrium, since a1(x0) = c1 × X1(0) = c2 × X2(0) = a2(x0). It can be shown [22] that X2(t) is a Poisson random variable with mean equal to 40. References [22, 23] sought to estimate P(E R ) = Pt≤100(X2 → θ|x0), the probability of X2(t) = θ for t ≤ 100 and several values of θ between 65 and 80. Since θ is about four to six standard deviations above the mean value 40, Pt≤100(X2 → θ|x0) is very small.
Kuwahara and Mura [22] employed the wSSA to estimate P(E
R
) and used b1(x) = δa1(x) and b2(x) = 1/δa2(x) with δ = 1.2 for four different values of θ: 65, 70, 75 and 80. Gillespie et al. [23] applied the refined wSSA to estimate P(ER) and used the same way to determine b1(x) and b2(x) but found that δ = 1.2 is near optimal for θ = 65 and that δ = 1.3 is near optimal for θ = 80. We repeated the simulation of Gillespie et al. [23] for θ = 65, 70, 75 and 80 with δ = 1.2, 1.25, 1.25 and 1.3, respectively. We then applied the wSSAps and the wNRMps to estimate P(E
R
) for θ = 65, 70, 75 and 80. This system has only two types of reaction: R1 is a G1 reaction and R2 is a G2 reaction. Since the system is at equilibrium with a0(x0) = 2,  with T = 100 is estimated to be 200, and thus
with T = 100 is estimated to be 200, and thus  . Using (19), we get
. Using (19), we get  and q2 = 1 - q1.
and q2 = 1 - q1.
Table 1 gives the estimated probability  and the sample variance σ2 for the wNRMps, the wSSAps and the refined wSSA, obtained from 107 simulation runs with θ = 65, 70, 75 and 80. It is seen that
and the sample variance σ2 for the wNRMps, the wSSAps and the refined wSSA, obtained from 107 simulation runs with θ = 65, 70, 75 and 80. It is seen that  is almost identical for all three methods. However, the wNRMps and the wSSAps provide variance almost two order of magnitude lower than the refined wSSA for θ = 80, or less than or almost one order of magnitude lower than the refined wSSA for θ = 75, 70 and 65. Moreover, the wNRMps and the wSSAps need about 60 and 70% CPU time of the refined wSSA, respectively. Note that the CPU time for the refined wSSA in Table 1 does not include the time needed for searching for the optimal value of δ for each θ. The less CPU time used by the wNRMps is expected since it only requires to generate one random variable in each step, whereas the wSSAps and the refined wSSA need to generate two random variables. It is also reasonable that the wSSAps requires less CPU time than the refined wSSA, because the wSSAps needs less computation to calculate the probability of each reaction in each step. Figure 1 compares the standard deviation
is almost identical for all three methods. However, the wNRMps and the wSSAps provide variance almost two order of magnitude lower than the refined wSSA for θ = 80, or less than or almost one order of magnitude lower than the refined wSSA for θ = 75, 70 and 65. Moreover, the wNRMps and the wSSAps need about 60 and 70% CPU time of the refined wSSA, respectively. Note that the CPU time for the refined wSSA in Table 1 does not include the time needed for searching for the optimal value of δ for each θ. The less CPU time used by the wNRMps is expected since it only requires to generate one random variable in each step, whereas the wSSAps and the refined wSSA need to generate two random variables. It is also reasonable that the wSSAps requires less CPU time than the refined wSSA, because the wSSAps needs less computation to calculate the probability of each reaction in each step. Figure 1 compares the standard deviation  of
of  for the wSSAps and the refined wSSA with different number of runs, n. Since the wNRMps provides almost the same standard deviation as the wSSAps, we do not plot it in the figure. It is seen that the wSSAps consistently yields much smaller standard deviation than the refined wSSA for all values of n. It was shown in [24] that the dwSSA yielded similar variance comparing to the refined wSSA. Therefore, our parameter selection method also substantially outperforms the dwSSA in this example.
for the wSSAps and the refined wSSA with different number of runs, n. Since the wNRMps provides almost the same standard deviation as the wSSAps, we do not plot it in the figure. It is seen that the wSSAps consistently yields much smaller standard deviation than the refined wSSA for all values of n. It was shown in [24] that the dwSSA yielded similar variance comparing to the refined wSSA. Therefore, our parameter selection method also substantially outperforms the dwSSA in this example.
 and the sample variance σ2 as well as the CPU time (in s) with 107 runs of the wNRMps, the wSSAps and the refined wSSA for the single species production-degradation model (31): (a) θ = 65 and 70 and (b) θ = 75 and 80
and the sample variance σ2 as well as the CPU time (in s) with 107 runs of the wNRMps, the wSSAps and the refined wSSA for the single species production-degradation model (31): (a) θ = 65 and 70 and (b) θ = 75 and 805.2 A reaction system with G1, G2and G3reactions
The previous system only contains a G1 reaction and a G2 reaction. We used the following system with G1, G2 and G3 reactions to test the wNRMps and the wSSAps:

In this system, a monomer S1 converts to S2 with a probability rate constant c1, while S2 is degraded with a probability rate constant c2. Meanwhile, another species S3 synthesizes S1 with a probability rate constant c3 and S1 degrades with a probability rate constant c4. In our simulations, we used the following values for the probability rate constants and the initial state:

and

This system is at equilibrium and the mean value of X2(t) is 40. We are interested in P (E
R
) = Pt≤10(X2 → θ|x(0)), the probability of X2(t) = θ for t ≤ 10. We chose θ = 65 and 68 in our simulations. To apply the wSSAps and the wNRMps to estimate P(ER), we divide the system into three groups. The G1 group contains reaction R1; the G2 group includes reaction R2; the G3 group consists of reactions R3 and R4. When fine-tuning the parameters, we further divided G3 into a G31 group which contains reaction R3 and a G32 group which contains reaction R4. Since the system is at equilibrium and we have a0(x0) = 20, a1(x0) = 4, a2(x0) = 4, a3(x0) = 8 and a4(x0) = 4, we get  ,
,  ,
,  ,
,  and
and  . Therefore, we get
. Therefore, we get  and the following probabilities:
and the following probabilities:  ,
,  and
and  .
.
If θ = 65, we have η = 25. Using (23), we obtained κ = 29. Substituting κ into (24), we got  ,
,  and
and  . We then chose α = 0.85 and β = 0.80 and calculated
. We then chose α = 0.85 and β = 0.80 and calculated  and
and  from (26) as
from (26) as  and
and  . Similarly, if θ = 68, we got κ = 26, which resulted in
. Similarly, if θ = 68, we got κ = 26, which resulted in  and
and  . Again, selecting α = 0.85 and β = 0.80, we got
. Again, selecting α = 0.85 and β = 0.80, we got  and
and  . To test whether the wNRMps and the wSSAps are sensitive to parameters α and β, we also used another set of parameters α = 0.80 and β = 0.75.
. To test whether the wNRMps and the wSSAps are sensitive to parameters α and β, we also used another set of parameters α = 0.80 and β = 0.75.
In order to compare the performance of the wNRMps and the wSSAps with that of the refined wSSA, we also ran simulations with the refined wSSA. In the refined wSSA, we chose the following parameters γ1 = δ, γ2 = 1/δ and γ
m
= 1, m = 3, 4 to adjust propensity functions. Since the optimal value of α is unknown, we ran the refined wSSA for δ = 1.2, 1.25, 1.3, 1.35, 1.40, 1.45, 1.50, 1.55, 1.60, 1.65, 1.70, 1.75 and 1.80 to determine the best δ. Figure 2 shows the variance of  obtained from the simulations with the refined wSSA and the wSSAps. Since the wNRMps yielded almost the same variance as the wSSAps, we only plotted the variance obtained from the wSSAps. It is seen that the wSSAps provides variance more than one order of magnitude lower than that provided by refined wSSA with the best δ. Is also observed that the wSSAps is not very sensitive to the parameters α and β, since the variance obtained with two different sets of values for α and β is almost the same.
obtained from the simulations with the refined wSSA and the wSSAps. Since the wNRMps yielded almost the same variance as the wSSAps, we only plotted the variance obtained from the wSSAps. It is seen that the wSSAps provides variance more than one order of magnitude lower than that provided by refined wSSA with the best δ. Is also observed that the wSSAps is not very sensitive to the parameters α and β, since the variance obtained with two different sets of values for α and β is almost the same.
Variance σ2 obtained from 107 runs of the wSSAps and the refined wSSA for the system in (32) with c 1 = 0.1, c 2 = 0.1, c 3 = 8, c 4 = 0.1, X 1 (0) = 40, X 2 (0) = 40 and X 3 (0) = 1. wSSAps para 1 represents the wSSAps without fine-tuning the probability of reactions in G3 group; wSSAps para 2 and 3 represent the wSSAps with fine-tuning the probability of reactions in G3 group using two sets of parameters: α = 0.85, β = 0.8 and α = 0.80, β = 0.75. Since the variance of the wSSAps does not depend on δ used in the refined wSSA, it appears as a horizontal line.
Table 2 lists  and its variance obtained from n = 107 runs of the refined wSSA, the wNRMps and the wSSAps. We first ran the wNRMps and the wSSAps without fine-tuning the probability of reactions in G3 group and calculated q
m
using (25). We then ran the wNRMps and the wSSAps with fine-tuning the probability of reactions in G3 group and used two sets of parameters (α = 0.85, β = 0.80; α = 0.80, β = 0.75) and (26) to calculate q
m
for the reactions in G3 group. We also made 1011 runs of the exact SSA to estimate
and its variance obtained from n = 107 runs of the refined wSSA, the wNRMps and the wSSAps. We first ran the wNRMps and the wSSAps without fine-tuning the probability of reactions in G3 group and calculated q
m
using (25). We then ran the wNRMps and the wSSAps with fine-tuning the probability of reactions in G3 group and used two sets of parameters (α = 0.85, β = 0.80; α = 0.80, β = 0.75) and (26) to calculate q
m
for the reactions in G3 group. We also made 1011 runs of the exact SSA to estimate  . It is seen that the wNRMps, the wSSAps and the refined wSSA all yield the same
. It is seen that the wNRMps, the wSSAps and the refined wSSA all yield the same  as the exact SSA. However, the wNRMps and the wSSAps with fine-tuning the probabilities of G3 reactions offer variance more than one order of magnitude lower than that provided by the refined wSSA. Without fine-tuning the probabilities of G3 reactions, the wNRMps and the wSSAps provided a little bit larger variance but still almost one order of magnitude lower than that provided by the refined wSSA. Table 2 also shows that the wNRMps and the wSSAps needed only 60-70% CPU time needed by the refined wSSA. Again, the CPU time of the refined wSSA in Table 2 does not include the time needed for searching for the optimal value of δ for each θ. If we include this time, the CPU time of the refined wSSA will be almost doubled.
as the exact SSA. However, the wNRMps and the wSSAps with fine-tuning the probabilities of G3 reactions offer variance more than one order of magnitude lower than that provided by the refined wSSA. Without fine-tuning the probabilities of G3 reactions, the wNRMps and the wSSAps provided a little bit larger variance but still almost one order of magnitude lower than that provided by the refined wSSA. Table 2 also shows that the wNRMps and the wSSAps needed only 60-70% CPU time needed by the refined wSSA. Again, the CPU time of the refined wSSA in Table 2 does not include the time needed for searching for the optimal value of δ for each θ. If we include this time, the CPU time of the refined wSSA will be almost doubled.
 and the sample variance σ2 as well as the CPU TIME (in s) with 107 runs of the wNRMps, the wSSAps and the refined wSSA for the system given in (32): (a) θ = 65 and (b) θ = 68
and the sample variance σ2 as well as the CPU TIME (in s) with 107 runs of the wNRMps, the wSSAps and the refined wSSA for the system given in (32): (a) θ = 65 and (b) θ = 685.3 Enzymatic futile cycle model
The enzymatic futile cycle model used in [22, 23] consists of two instances of the elementary single-substrate enzymatic reaction described by the following six reactions:

This system essentially consists of a forward-reverse pair of enzyme-substrate reactions, with the conversion of S2 into S5 catalyzed by S1 in the first three reactions and the conversion of S5 into S2 catalyzed by S4 in the last three reactions. We used the same probability rate constants and initial state as used in [22, 23]:

and

With the above rate constants and initial state, X2(t) and X2(5) tend to equilibrate about their initial value 50. References [22, 23] sought to estimate P(E R ) = Pt≤100(X5 → θ|x(0)), the probability that X5(t) = θ for t ≤ 100 and several values of θ between 25 and 40. We repeated simulations with the refined wSSA in [23] for θ = 25 and 40. The refined wSSA employed the following parameters γ3 = δ, γ6 = 1/δ and γ m = 1, m = 1, 2, 4, 5, and we used the best value of δ determined in [23]: δ = 0.35 for θ = 25 and δ = 0.60 for θ = 40.
In this system, we always have X2(t) + X5(t) = 100. So when the rare event occurs at time t, we have X5(t) = θ and X2(t) = 100 - θ. The rare event is therefore defined as X5 = 50 + η with η = θ - 50 or equivalently X2 = 50 - η. According to the partition rule defined in Section 4, R3 is a G2 reaction; R6 is a G1 reaction; R1, R2, R4 and R5 are G3 reactions.
We ran Gillespie's SSA 103 times and got an estimate of  as
as  , and thus
, and thus  . When θ = 40, we have η = -10. Using (23) and K
E
= 432, we obtained κ = 6 Substituting κ into (24), we got
. When θ = 40, we have η = -10. Using (23) and K
E
= 432, we obtained κ = 6 Substituting κ into (24), we got  ,
,  and
and  . In this example, there always have certain reactions whose propensity functions are zero, since we always have X1(t) + X3(t) = 1 and X4(t) + X6(t) = 1. Due to this special property, we calculate the probability of each reaction as follows. The system has only 4 states in terms of X3(t) and X6(t): X3(t)X6(t) = 11, 01, 10 or 00. From the 103 runs of Gillespie's exact SSA, we estimated the probability of reactions occurring in reach state as P11 ≈ 1/2, P01 = P10 ≈ 1/4 and P00 ≈ 0. Note that reaction R6 only occurs in states 11 and 01 and we denote its probability in these two states used in the wSSAps as
. In this example, there always have certain reactions whose propensity functions are zero, since we always have X1(t) + X3(t) = 1 and X4(t) + X6(t) = 1. Due to this special property, we calculate the probability of each reaction as follows. The system has only 4 states in terms of X3(t) and X6(t): X3(t)X6(t) = 11, 01, 10 or 00. From the 103 runs of Gillespie's exact SSA, we estimated the probability of reactions occurring in reach state as P11 ≈ 1/2, P01 = P10 ≈ 1/4 and P00 ≈ 0. Note that reaction R6 only occurs in states 11 and 01 and we denote its probability in these two states used in the wSSAps as  and
and  and its natural probability as
and its natural probability as  and
and  . The probability
. The probability  can be calculated as
can be calculated as  and
and  can be approximated as
can be approximated as  assuming X2(t) = 50 since the system is in equilibrium. Then, using the relationships:
assuming X2(t) = 50 since the system is in equilibrium. Then, using the relationships:  and
and  , we get
, we get  and
and  . Reaction R3 only occurs in states 11 and 10 and its probability can be obtained similarly as
. Reaction R3 only occurs in states 11 and 10 and its probability can be obtained similarly as  and
and  . In a state s (s = 11, 01, 10 or 00), we calculate
. In a state s (s = 11, 01, 10 or 00), we calculate  and then calculated
and then calculated  , m = 1, 2, 4 and 5, from (25). Surprisingly,
, m = 1, 2, 4 and 5, from (25). Surprisingly,  ,
,  ,
,  and
and  we calculated are very close to the values used in the refined wSSA which were obtained by making 105 runs of the refined wSSA for each of seven guessed values of γ. In contrast, we do not need to guess the values of parameters but calculate them analytically, and all the information needed in our calculation was obtained from 103 of Gillespie's exact SSA, which incurs negligible computational overhead.
we calculated are very close to the values used in the refined wSSA which were obtained by making 105 runs of the refined wSSA for each of seven guessed values of γ. In contrast, we do not need to guess the values of parameters but calculate them analytically, and all the information needed in our calculation was obtained from 103 of Gillespie's exact SSA, which incurs negligible computational overhead.
When θ = 25, we have η = -25. Using (23) and  , we obtained κ = 3. Substituting κ into (24), we got
, we obtained κ = 3. Substituting κ into (24), we got  ,
,  and
and  . Similar to the previous calculation, we got
. Similar to the previous calculation, we got  ,
,  ,
,  and
and  and then calculated the probabilities of other reactions from (25). Again
and then calculated the probabilities of other reactions from (25). Again  ,
,  ,
,  and
and  we obtained are very close to the values used in the refined wSSA.
we obtained are very close to the values used in the refined wSSA.
Table 3 lists the simulation results obtained from 106 runs of the wNRMps, the wSSAps and the refined wSSA for θ = 40 and 25. It is seen that the estimated probability  and variance σ2 are almost identical for all three methods, which is expected because the probability of each reaction in three methods is almost the same. This implies that all three methods may have used near optimal values for the importance sampling parameters. However, in the previous two systems, the parameters used by the refined wSSA are far away from their optimal values, because the wSSAps and the wNRMps provided much lower variance than the refined wSSA. It is also seen from Table 3 that the wSSAps used almost the same CPU time as that used by the refined wSSA and that the wNRMps used about 80% of the CPU time of the refined wSSA. Again, the CPU time of the refined wSSA does not include the time needed to find the optimal value of δ. Figure 3 depicts the standard deviation of the estimated probability versus the number of simulation runs n for the wSSAps and the refined wSSA. Since the wNRMps provides almost the same standard deviation as the wSSAps, we did not plot it in the figure. It is again seen that the wSSAps and the refined wSSA yield almost the same standard deviation for all values of n in this case. It was demonstrated in [24] that the dwSSA yielded comparable variance as the refined wSSA. Therefore, our parameter selection method offers similar performance to the dwSSA in this example.
and variance σ2 are almost identical for all three methods, which is expected because the probability of each reaction in three methods is almost the same. This implies that all three methods may have used near optimal values for the importance sampling parameters. However, in the previous two systems, the parameters used by the refined wSSA are far away from their optimal values, because the wSSAps and the wNRMps provided much lower variance than the refined wSSA. It is also seen from Table 3 that the wSSAps used almost the same CPU time as that used by the refined wSSA and that the wNRMps used about 80% of the CPU time of the refined wSSA. Again, the CPU time of the refined wSSA does not include the time needed to find the optimal value of δ. Figure 3 depicts the standard deviation of the estimated probability versus the number of simulation runs n for the wSSAps and the refined wSSA. Since the wNRMps provides almost the same standard deviation as the wSSAps, we did not plot it in the figure. It is again seen that the wSSAps and the refined wSSA yield almost the same standard deviation for all values of n in this case. It was demonstrated in [24] that the dwSSA yielded comparable variance as the refined wSSA. Therefore, our parameter selection method offers similar performance to the dwSSA in this example.
 and the sample variance σ2 as well as the CPU TIME (in s) with 106 runs of the wNRMps, the wSSAps and the refined wSSA for the enzyme futile cycle model (35): (a) θ = 25 and (b) θ = 40
and the sample variance σ2 as well as the CPU TIME (in s) with 106 runs of the wNRMps, the wSSAps and the refined wSSA for the enzyme futile cycle model (35): (a) θ = 25 and (b) θ = 40The SD of the estimated probability versus the number of simulation runs n obtained with the refined wSSA and the wSSAps for the enzymatic futile cycle model (35) with c 1 = c 2 = c 4 = c 5 = 1, c 3 = c 6 = 0.1, X 1 (0) = X 4 (0) = 1, X 2 (0) = X 5 (0) = 50 and X 3 (0) = X 6 (0) = 0 for θ = 25 and 40.
6 Conclusion
The wSSA and the refined wSSA are innovative variation of Gillespie's standard SSA. They provide an efficient way for estimating the probability of rare events that occur in chemical reaction systems with an extremely low probability in a given time period. The wSSA was developed based on the directed method of the SSA. In this paper, we developed an alternative wNRM for estimating the probability of the rave event. We also devised a systematic method for selecting the values of importance sampling parameters, which is absent in the wSSA and the refined wSSA.
This parameter selection method was then incorporated into the wSSA and the wNRM. Numerical examples demonstrated that comparing with the refined wSSA and the dwSSA, the wSSA and the wNRM with our parameter selection procedure could substantially reduce the variance of the estimated probability of the rare event and speed up simulation.
Competing interets
The author declares that they have no competing interests.
Abbreviations
- NRM:
-
next reaction method
- wNRM:
-
weighted NRM
- wSSA:
-
weighted stochastic simulation algorithm.
References
Kærn M, Elston TC, Blake WJ, Collins JJ: Stochasticity in gene expression: from theories to phenotypes. Nat Rev Genet 2005, 6: 451-464. 10.1038/nrg1615
Gillespie DT: A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J Comput Phys 1976, 22: 403-434. 10.1016/0021-9991(76)90041-3
Gillespie DT: Exact stochastic simulation of coupled chemical reaction. J Phys Chem 1977, 81: 2340-2361. 10.1021/j100540a008
Gibson MA, Bruck J: Exact stochastic simulation of chemical systems with many species and many channels. J Phys Chem A 2000, 105: 1876-1889.
Cao Y, Li H, Petzold LR: Efficient formulation of the stochastic simulation algorithm for chemically reacting systems. J Chem Phys 2004,121(9):4059-4067. 10.1063/1.1778376
Cai X: Exact stochastic simulation of coupled chemical reactions with delays. J Chem Phys 2007, 126: 124108. 10.1063/1.2710253
Anderson DF: A modified next reaction method for simulating systems with time varying rate constants and systems with delays. J Chem Phys 2007,127(21):214107. 10.1063/1.2799998
Gillespie DT: Approximate accelerated stochastic simulation of chemically reacting systems. J Chem Phys 2001, 115: 1716-1733. 10.1063/1.1378322
Gillespie DT, Petzold LR: Improved leap-size selection for accelerated stochastic simulation. J Chem Phys 2003,119(6):8229-8234. 10.1063/1.1613254
Tian T, Burrage K: Binomial leap methods for simulating stochastic chemical kinetics. J Chem Phys 2004, 121: 10356-10364. 10.1063/1.1810475
Chatterjee A, Vlachos DG, Katsoulakis MA: Binomial distribution based τ -leap accelerated stochastic simulation. J Chem Phys 2005, 122: 024112. 10.1063/1.1833357
Cao Y, Gillespie DT, Petzold LR: Efficient step size selection for the tau-leap simulation method. J Chem Phys 2006,124(4):044109. 10.1063/1.2159468
Cao Y, Gillespie D, Petzold L: Multiscale stochastic simulation algorithm with stochastic partial equilibrium assumption for chemically reacting systems. J Comput Phys 2005, 206: 395-411. 10.1016/j.jcp.2004.12.014
Goutsias J: Quasiequlibrium approximation of fast reaction kinetics in stochastic biochemical systems. J Chem Phys 2005, 122: 184102. 10.1063/1.1889434
Haseltine EL, Rawlings JB: Approximate simulation of coupled fast and slow reactions for stochastic chemical kinetics. J Chem Phys 2002,117(15):6959-6969. 10.1063/1.1505860
Rao CV: AP Arkin, Stochastic chemical kinetics and the quasi-steady-state assumption: application to the Gillespie algorithem. J Chem Phys 2003,18(11):4999-5010.
Salis H, Kaznessis Y: Accurate hybrid stochastic simulation of a system of coupled chemical or biochemical reactions. J Chem Phys 2005, 122: 54103.1-54103.13.
Auger A, Chatelain P, Koumoutsakos P: R-leaping: accelerating the stochastic simulation algorithm by reaction leaps. J Chem Phys 2006,125(8):084103-084115. 10.1063/1.2218339
Cai X, Xu Z: K-leap methods for accelerating stochastic simulation of chemically reacting systems. J Chem Phys 2007,126(7):074102. 10.1063/1.2436869
Csete M, Doyle J: Bow ties, metabolism and disease. Trends Biotechnol 2004, 22: 446-450. 10.1016/j.tibtech.2004.07.007
Egger G, Liang G, Aparicio A, Jones PA: Epigenetics in human disease and prospects for epigenetic therapy. Nature 2004, 429: 457. 10.1038/nature02625
Kuwahara H, Mura I: An efficient and exact stochastic simulation method to analyze rare events in biochemical systems. J Chem Phys 2008, 129: 165101. 10.1063/1.2987701
Gillespie DT, Roh M, Petzold LR: Refining the weighted stochastic simulation algorithm. J Chem Phys 2009, 130: 174103. 10.1063/1.3116791
Daigle BJ: M Roh, DT Gillespie, LR Petzold, Automated estimation of rare event probabilities in biochemical systems. J Chem Phys 2010, 134: 044110.
Rubinstein RY, Kroese DP: The Cross-Entropy Method. A Unified Approach to Combinatorial Optimization, Monte-Carlo Simulation and Machine Learning. Springer; 2004.
Liu JS: Monte Carlo Strategies in Scientific Computing. Springer; 2001.
Bucklew JA: Introduction to Rare Event Simulation. Springer, New York; 2004.
Rubino G, Tuffin B, (eds): Rare Event Simulation using Monte Carlo Methods. Wiley, New York; 2009.
L'Ecuyer P, Tuffin B: Effective approximation of zero-variance simulation in a reliability setting. Proc. European Simulation Modelling Conf. (ESM'2007), St. Julians, Malta 2007, 48-57.
Gillespie DT: The chemical Langevin equation. J Chem Phys 2000,113(1):297-306. 10.1063/1.481811
Xu Z, Cai X: Unbiased tau-leap methods for stochastic simulation of chemically reacting systems. J Chem Phys 2008,128(15):154112. 10.1063/1.2894479
Acknowledgements
This work was supported by the National Science Foundation (NSF) under NSF CAREER Award no. 0746882.
Author information
Authors and Affiliations
Corresponding author
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xu, Z., Cai, X. Weighted next reaction method and parameter selection for efficient simulation of rare events in biochemical reaction systems. J Bioinform Sys Biology 2011, 4 (2011). https://doi.org/10.1186/1687-4153-2011-797251
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-4153-2011-797251