Abstract
In this study, a new solution scheme for the partial differential equations with variable coefficients defined on a large domain, especially including infinities, has been investigated. For this purpose, a spectral basis, called exponential Chebyshev (EC) polynomials, has been extended to a new kind of double Chebyshev polynomials. Many outstanding properties of those polynomials have been shown. The applicability and efficiency have been verified on an illustrative example.
MSC:35A25.
Similar content being viewed by others
1 Introduction
The importance of special functions and orthogonal polynomials occupies a central position in the numerical analysis. Most common solution techniques of differential equations with these polynomials can be seen in [1–12]. One of the most important of those special functions is Chebyshev polynomials. The well-known first kind Chebyshev polynomials [1] are orthogonal with respect to the weight-function on the interval . These polynomials have many applications in different areas of interest, and a lot of studies are devoted to show the merits of them in various ways. One of the application fields of Chebyshev polynomials can appear in the solution of differential equations. For example, Chebyshev polynomial approximations have been used to solve ordinary differential equations with boundary conditions in [1], with collocation points in [13], the general class of linear differential equations in [14, 15], linear-integro differential equations with collocation points in [16], the system of high-order linear differential and integral equations with variable coefficients in [17, 18], and the Sturm-Liouville problems in [19].
Some of the fundamental ideas of Chebyshev polynomials in one-variable techniques have been extended and developed to multi-variable cases by the studies of Fox et al. [1], Basu [20], Doha [21] and Mason et al. [5]. In recent years, the Chebyshev matrix method for the solution of partial differential equations (PDEs) has been proposed by Kesan [22] and Akyuz-Dascioglu [23] as well.
On the other hand, all of the above studies are considered on the interval in which Chebyshev polynomials are defined. Therefore, this limitation causes a failure of the Chebyshev approach in the problems that are naturally defined on larger domains, especially including infinity. Then, Guo et al. [24] has proposed a modified type of Chebyshev polynomials as an alternative to the solutions of the problems given in a nonnegative real domain. In his study, the basis functions called rational Chebyshev polynomials are orthogonal in and are defined by
Parand et al. and Sezer et al. successfully applied spectral methods to solve problems on semi-infinite intervals [25, 26]. These approaches can be identified as the methods of rational Chebyshev Tau and rational Chebyshev collocation, respectively. However, this kind of extension also fails to solve all of the problems over the whole real domain. More recently, we have introduced a new modified type of Chebyshev polynomials that is developed to handle the problems in the whole real range called exponential Chebyshev (EC) polynomials [27].
In this study, we have shown the extension of the EC polynomial method to multi-variable case, especially, to two-variable problems.
2 Properties of double EC polynomials
The well-known first kind Chebyshev polynomials are orthogonal in the interval with respect to the weight-function and can be simply determined with the help of the recurrence formula [1]
Therefore, the exponential Chebyshev (EC) functions are recently defined in a similar fashion as follows [27].
Let
be a function space with the weight function . We also assume that, for a nonnegative integer n, the n th derivative of a function is also in . Then an EC polynomial can be given by

where .
This definition leads to the three-term recurrence equation for EC polynomials
This definition also satisfies the orthogonality condition [27]
where and is the Kronecker function.
Double EC functions
Basu [20] has given the product which is a form of bivariate Chebyshev polynomials. Mason et al. [5] and Doha [11] have also mentioned a Chebyshev polynomial expression for an infinitely differentiable function defined on the square by
where and are Chebyshev polynomials of the first kind, and the double primes indicate that the first term is ; and are to be taken as and for , respectively.
Definition
Based on Basu’s study, now we introduce double EC polynomials in the following form:
where , are EC polynomials defined by
Recurrence relation The polynomial satisfies the recurrence relations


If the function is continuous throughout the whole infinite domain , then the ’s are biorthogonal with respect to the weight function
and we have
Multiplication is said to be of higher order than if . Then the following result holds:

Function approximation
Let be an infinitely differentiable function defined on the square . Then it may be expressed in the form
where
If in Eq. (2.10) is truncated up to the m th and n th terms, then it can be written in the matrix form
with is a EC polynomial matrix with entries ,
and A is an unknown coefficient vector,
Matrix relations of the derivatives of a function
th-order partial derivative of can be written as
and its matrix form is
where , and
Proposition 1 Let and th-order derivative be given by (2.12) and (2.16), respectively. Then there exists a relation between the double EC coefficient row vector and th-order partial derivatives of the vector of size as
where and are operational matrices for partial derivatives given in the following forms:
and

Here, I and O are identity and zero matrices, respectively, and T denotes the usual matrix transpose.
Proof Taking the partial derivatives of , and both sides of the recurrence relation (2.5) with respect to x, we get


and
By using the relations (2.18)-(2.20) for the elements of the matrix of partial derivatives can be obtained from the following equalities:
Similarly, taking the partial derivatives of , and both sides of the recurrence relation (2.6) with respect to y, respectively, we write


and
Then with the help of the relations (2.22)-(2.24), the elements of the matrices of partial derivatives can be obtained from
We have noted here that for and for .
From (2.21) and (2.25), the following equalities hold for and
and
where and and I denotes identity matrix.
Then utilizing the equalities in (2.26) and (2.27), the explicit relation between the double EC polynomial row vector and those of its derivatives has been proved as follows:
or
□
Remark .
Corollary From Eqs. (2.16) and (2.17), it is clear that the derivatives of the function are expressed in terms of double EC coefficients as follows:
3 Collocation method with double EC polynomials
In the process of obtaining the numerical solutions of partial differential equations with the double EC method, the main idea or major step is to evaluate the necessary Chebyshev coefficients of the unknown function. So, in Section 2, we give the explicit relations between the polynomials of an unknown function and those of its derivatives for different nonnegative integer values of i and j.
In this section, we consider the higher-order linear PDE with variable coefficients of a general form
with the conditions mentioned in [23] as three possible cases:
and/or
and/or
Here, , and , , , , , are known functions on the square . We now describe an approximate solution of this problem by means of double EC series as defined in (2.10). Our aim is to find the EC coefficients in the vector A. For this reason, we can represent the given problem and its conditions by a system of linear algebraic equations by using collocation points.
Now, the collocation points can be determined in the inner domain as
and at the boundaries
-
(i)
and ,
-
(ii)
and .
Since EC polynomials are convergent at both boundaries, namely their values are either 1 or −1, the appearance of infinity in the collocation points does not cause a loss in the method.
Therefore, when we substitute the collocation points into the problem (3.1), we get
The system (3.6) can be written in the matrix form as follows:
where denotes the diagonal matrix with the elements (; ) and F denotes the column matrix with the elements (; ).
Putting the collocation points into derivatives of the unknown function as in Eq. (2.28) yields
where E is the block matrix given by
and for , we see
Therefore, from Eq. (3.7), we get a system of the matrix equation for the PDE
which corresponds to a system of linear algebraic equations with unknown double EC coefficients .
It is also noted that the structures of matrices and F vary according to the number of collocation points and the structure of the problem. However, E, and do not change their nature for fixed values of m and n which are truncation limits of the EC series. In other words, the changes in E, and are just dependent on the number of collocation points.
Briefly, we can denote the expression in the parenthesis of (3.10) by W and write
Then the augmented matrix of Eq. (3.11) becomes
Applying the same procedure for the given conditions (3.2)-(3.4), we have



Then these can be written in a compact form
where V is an matrix and R is an matrix, so that h is the rank of all row matrices belonging to the given condition. The augmented matrices of the conditions become
Consequently, (3.12) together with (3.17) can be written in a new augmented matrix form
This form can be achieved by replacing some rows of (3.12) by the rows of (3.17) accordingly, or adding those rows to the matrix (3.12) provided that . Then it can be written in the following compact form:
Finally, the vector A (thereby the coefficients ) is determined by applying some numerical methods (e.g., Gauss elimination) designed especially to solve the system of linear equations. Therefore, the approximate solution can be obtained. In other words, it gives the double EC series solution of the problem (3.1) with given conditions.
4 Illustration
Now, we give an example to show the ability and efficiency of the double EC polynomial approximation method.
Example
Let us consider the linear partial differential equation
with the conditions
It is known that the exact solution of the problem is .
Absolute errors of the proposed procedure at the grid points are tabulated for in Table 1.
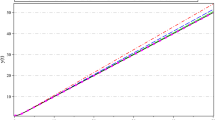
Contour plots of the exact solutions and the approximate solutions are given for the region in (a) and (b) and for the region , in (c) and (d) of Figure 1, respectively. Figure 2 shows a graphical representation of the exact solution and, for , the approximate solution of the example.
5 Conclusion
In this article, a new solution scheme for the partial differential equation with variable coefficients defined on unbounded domains has been investigated and EC polynomials have been extended to double EC polynomials to solve multi-variable problems. It is also noted that the double EC-collocation method is very effective and has a direct ability to solve multi-variable (especially two-variable) problems in the infinite domain. For computational purposes, this approach also avoids more computations by using sparse operational matrices and saves much memory. On the other hand, the double EC polynomial approach deals directly with infinite boundaries, and their operational matrices are of few non-zero entries lain along two subdiagonals.
References
Fox L, Parker IB: Chebyshev Polynomials in Numerical Analysis. Oxford University Press, London; 1968. [Revised 2nd edition,1972]
Lebedev NN: Special Functions and Their Applications. Prentice Hall, London; 1965. [Revised Eng. Ed.: Translated and Edited by Silverman, RA (1972)]
Yudell LL: The special functions and their approximations V-2. 53. In Mathematics in Science and Engineering. Edited by: Bellman R. Academic Press, New York; 1969.
Wang ZX, Guo DR: Special Functions. World Scientific, Singapore; 1989.
Mason JC, Handscomb DC: Chebyshev Polynomials. CRC Press, Boca Raton; 2003.
Marcellan F, Assche WV (Eds): Lecture Notes in Mathematics In Orthogonal Polynomials and Special Functions: Computation and Applications. Springer, Heidelberg; 2006.
Mathai AM, Haubold HJ: Special Functions for Applied Scientists. Springer, New York; 2008.
Agarwal RP, O’Regan D: Ordinary and Partial Differential Equations with Special Functions Fourier Series and Boundary Value Problems. Springer, New York; 2009.
Schwartz AL: Partial differential equations and bivariate orthogonal polynomials. J. Symb. Comput. 1999, 28: 827-845. Article ID Jsco.1999.0342 10.1006/jsco.1999.0342
Makukula ZG, Sibanda P, Motsa SS: A note on the solution of the Von Karman equations using series and Chebyshev spectral methods. Bound. Value Probl. 2010., 2010: Article ID 471793
Doha EH, Bhrawy AH, Saker MA: On the derivatives of Bernstein polynomials: an application for the solution of high even-order differential equations. Bound. Value Probl. 2011., 2011: Article ID 829543
Xu Y: Orthogonal polynomials and expansions for a family of weight functions in two variables. Constr. Approx. 2012, 36: 161-190. 10.1007/s00365-011-9149-4
Wright K: Chebyshev collocation methods for ordinary differential equations. Comput. J. 1964, 6(4):358-365. 10.1093/comjnl/6.4.358
Scraton RE: The solution of linear differential equations in Chebyshev series. Comput. J. 1965, 8(1):57-61. 10.1093/comjnl/8.1.57
Sezer M, Kaynak M: Chebyshev polynomial solutions of linear differential equations. Int. J. Math. Educ. Sci. Technol. 1996, 27(4):607-618. 10.1080/0020739960270414
Akyüz A, Sezer M: A Chebyshev collocation method for the solution of linear integro-differential equations. Int. J. Comput. Math. 1999, 72: 491-507. 10.1080/00207169908804871
Akyüz A, Sezer M: Chebyshev polynomial solutions of systems of high-order linear differential equations with variable coefficients. Appl. Math. Comput. 2003, 144: 237-247. 10.1016/S0096-3003(02)00403-4
Akyüz-Daşcıoğlu A: Chebyshev polynomial solutions of systems of linear integral equations. Appl. Math. Comput. 2004, 151: 221-232. 10.1016/S0096-3003(03)00334-5
Celik I, Gokmen G: Approximate solution of periodic Sturm-Liouville problems with Chebyshev collocation method. Appl. Math. Comput. 2005, 170(1):285-295. 10.1016/j.amc.2004.11.038
Basu NK: On double Chebyshev series approximation. SIAM J. Numer. Anal. 1973, 10(3):496-505. 10.1137/0710045
Doha EH: The Chebyshev coefficients of the general order derivative of an infinitely differentiable function in two or three variables. Ann. Univ. Sci. Bp. Rolando Eötvös Nomin., Sect. Comput. 1992, 13: 83-91.
Kesan C: Chebyshev polynomial solutions of second-order linear partial differential equations. Appl. Math. Comput. 2003, 134: 109-124. 10.1016/S0096-3003(01)00273-9
Akyüz-Daşcıoğlu A: Chebyshev polynomial approximation for high-order partial differential equations with complicated conditions. Numer. Methods Partial Differ. Equ. 2009, 25: 610-621. 10.1002/num.20362
Guo B, Shen J, Wang Z: Chebyshev rational spectral and pseudospectral methods on a semi-infinite interval. Int. J. Numer. Methods Eng. 2002, 53: 65-84. 10.1002/nme.392
Parand K, Razzaghi M: Rational Chebyshev Tau method for solving higher-order ordinary differential equations. Int. J. Comput. Math. 2004, 81: 73-80.
Sezer M, Gülsu M, Tanay B: Rational Chebyshev collocation method for solving higher-order linear differential equations. Numer. Methods Partial Differ. Equ. 2011, 27(5):1130-1142. 10.1002/num.20573
Kaya, B, Kurnaz, A, Koc, AB: Exponential Chebyshev polynomials. Paper presented at the 3rd Conferences of the National Ereğli Vocational High School, University of Selcuk, Ereğli, 28-29 April, 2011 (In Turkısh)
Acknowledgements
This study was supported by the Research Projects Center (BAP) of Selcuk University. The authors would like to thank the editor and referees for their valuable comments and remarks which led to a great improvement of the article. Also, ABK and AK would like to thank the Selcuk University and TUBITAK for their support. We note here that this study was presented orally at the International Conference on Applied Analysis and Algebra (ICAAA 2012), Istanbul, 20-24 June, (2012).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
ABK wrote the first draft and AK corrected and improved the final version. All authors read and approved the final draft.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Koç, A.B., Kurnaz, A. A new kind of double Chebyshev polynomial approximation on unbounded domains. Bound Value Probl 2013, 10 (2013). https://doi.org/10.1186/1687-2770-2013-10
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2013-10