Existence and uniqueness of periodic solutions of second-order nonlinear differential equations

Abstract

This paper is concerned with the following second-order nonlinear differential equation:

$$x^{(2n)}(t)+\sum _{k=1}^{n+1}{f}_k(x^{(k-1)}(t))x^{(k)}(t)-g(t,x(t))=e(t).$$

By applying Mawhin’s continuation theorem of coincidence degree theory, we establish sufficient conditions for the existence and uniqueness of periodic solutions for the above equation. Some recent results are known as the special cases of ours.

1 Introduction

In applied science, some practical problems such as nonlinear oscillations [1, 2], fluid mechanical and nonlinear elastic mechanical phenomena [3–9] are associated with the periodic solutions of nonlinear high-order differential equations. Recently, Bereanu [10], Zhao et al. [11] and Fan et al. [12] investigated the existence of T-periodic solutions for the following fourth-order nonlinear differential equation:

$$x^{\prime \prime \prime \prime }(t)+a{x}^{‴}(t)-p{x}^{″}(t)+q{x}^{\prime }(t)-g(t,x(t))=e(t).$$

(1.1)

Xu et al. [13] dealt with the existence of T-periodic solutions for the second-order nonlinear differential equation as follows:

$$x^{(2n)}(t)+h(x^{(n)}(t))x^{(n+1)}(t)-P(x^{\prime }(t))x^{″}(t)+f(x(t))x^{\prime }(t)-g(t,x(t))=e(t),$$

(1.2)

where $n\ge 2$ is an even integer, $h,P,f,e:R\to R$ and $g:R^2\to R$ represent continuous functions, e and g respectively denote the T-periodic and T-periodic in the first argument and $T>0$. However, to the best of our knowledge, most authors mentioned above have only considered the existence of periodic solutions of Eqs. (1.1) and (1.2). There are still few studies on the uniqueness of periodic solutions for these equations. Thus, in this case, it is worth investigating both the existence and the uniqueness of periodic solutions for a high-order nonlinear differential equation.

In this paper, we study the existence and uniqueness of T-periodic solutions for the second-order nonlinear differential equation

$$x^{(2n)}(t)+\sum _{k=1}^{n+1}{f}_k(x^{(k-1)}(t))x^{(k)}(t)-g(t,x(t))=e(t),$$

(1.3)

where $n\ge 2$ is an even integer, $f_k,e:R\to R$ and $g:R^2\to R$ represent continuous functions and $f_k$ ($k=1,2,\dots ,n+1$) are bounded, e and g respectively denote the T-periodic and T-periodic in the first argument and $T>0$.

Obviously, Eq. (1.1) is a special case of Eq. (1.3) with $n=2$, $f_3(x)\equiv a$, $f_2(x)\equiv -p$ and $f_1(x)\equiv q$. Moreover, Eq. (1.2) is another special case of Eq. (1.3) with $f_3(x)=f_4(x)=\cdots =f_{n+1}(x)\equiv 0$.

For ease of exposition, we will adopt the following notations throughout this paper:

Let

$$C_T^m=\{x|x\in C^m(R,R),x(t+T)=x(t)\text{ for all }t\in R,m\in N\}$$

be Banach spaces with the norms

$${\parallel x\parallel }_{(m)}=\sum _{k=0}^m{\parallel x^{(k)}\parallel }_{\mathrm{\infty }}(x\in C_T^m).$$

To obtain our results, we also make the following assumptions:

(S1) There exists $d>0$ such that, for any continuous T-periodic function x, we have

$$[g(t,x(t))+e(t)]x(t)>0\text{for all }t\in R,|x(t)|\ge d$$

or

$$[g(t,x(t))+e(t)]x(t)<0\text{for all }t\in R,|x(t)|\ge d.$$

(S2) For $t,x_1,x_2\in R$, $x_1\ne x_2$,

$$[g(t,x_1)-g(t,x_2)](x_1-x_2)<0,1>L_1\frac{T}{\pi }{\left(\frac{T}{2\pi }\right)}^{2(n-1)}+\sum _{k=2}^{n+1}{L}_k{\left(\frac{T}{2\pi }\right)}^{2n-k}.$$

(S3) For $t,x_1,x_2\in R$, $x_1\ne x_2$, there exists a nonnegative constant B such that

$$B{(x_1-x_2)}^2\ge [g(t,x_1)-g(t,x_2)](x_1-x_2)>0,$$

and

$$1>L_1\frac{T}{\pi }{\left(\frac{T}{2\pi }\right)}^{2(n-1)}+\sum _{k=2}^{n+1}{L}_k{\left(\frac{T}{2\pi }\right)}^{2n-k}+B{\left(\frac{T}{\pi }\right)}^2{\left(\frac{T}{2\pi }\right)}^{2(n-1)}.$$

2 Preliminaries

The following lemmas will be useful to prove our main results in Section 3.

Let $\tilde{f}:R^{2n+1}\to R$ be a continuous function, T-periodic with respect to the first variable, and consider the second-order differential equation

(2.1)

Lemma 2.1 (See [14])

Assume that the following conditions hold.

• (i) There exists $\rho >0$ such that, for each $\lambda \in (0,1]$, one has that any possible T-periodic solution x of the problem

  

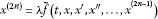
satisfies the a priori estimation ${\parallel x\parallel }_{(2n-1)}<\rho$.

• (ii) The continuous function $F:R\to R$ defined by

  $$F(x)={\int }_0^T\tilde{f}(t,x,0,0,\dots ,0)dt,x\in R$$

satisfies $F(-\rho )F(\rho )<0$.

Then (2.1) has at least one T-periodic solution x such that ${\parallel x\parallel }_{(2n-1)}<\rho$.

From Lemma 2.2 in [15] and the proof of inequality (10) in [[12], p.124], we obtain the following.

Lemma 2.2 Let $x(t)\in C_T^1$. Suppose that there exist two constants $D>0$, $t_0\in [0,T]$ such that $|x(t_0)|\le D$, then

$${\parallel x\parallel }_2\le \frac{T}{\pi }{\parallel x^{\prime }\parallel }_2+\sqrt{T}D,{\parallel x\parallel }_{\mathrm{\infty }}\le D+\frac{1}{2}\sqrt{T}{\parallel x^{\prime }\parallel }_2.$$

(2.2)

Lemma 2.3 (See [16, 17])

If $x\in C_T^2$, then

$${\parallel x^{\prime }\parallel }_2^2\le {\left(\frac{T}{2\pi }\right)}^2{\parallel x^{″}\parallel }_2^2.$$

(2.3)

Lemma 2.4 (See [13])

For any $x\in C_T^n$, one has that

$${\parallel x^{(k)}\parallel }_{\mathrm{\infty }}\le T^{(n-1)-k}{\left(\frac{1}{2}\right)}^{(n-1)-(k-1)}{\int }_0^T|x^{(n)}(t)|dt,k=1,2,\dots ,n-1.$$

(2.4)

Now, let

For $\lambda \in (0,1]$, we consider the second-order differential equation

(2.5)

Lemma 2.5 Suppose that (S1), (S2) (or (S3)) hold, then there exists a fixed constant $C^{\ast }>0$ independent of λ and x such that any possible T-periodic solution x of (2.5) satisfies

$${\parallel x^{(k)}\parallel }_{\mathrm{\infty }}\le C^{\ast },k=0,1,2,\dots ,n-1.$$

(2.6)

Proof Let $\lambda \in (0,1]$ and let x be a possible T-periodic solution of (2.5). Integrating (2.5) from 0 to T yields

$${\int }_0^T[g(t,x(t))+e(t)]dt=0,$$

which together with (S1) implies that

$$\mathrm{\exists }\xi \in [0,T]:|x(\xi )|<d.$$

In view of (2.2) and (2.3), we get

$${\parallel x\parallel }_{\mathrm{\infty }}\le d+\frac{1}{2}\sqrt{T}{\parallel x^{\prime }\parallel }_2\le d+\frac{T\sqrt{T}}{4\pi }{\parallel x^{″}\parallel }_2.$$

(2.7)

Thus

(2.8)

(2.9)

On the other hand, multiplying Eq. (2.5) by x and integrating it from 0 to T, we obtain

$$\begin{array}{rl}{\parallel x^{(n)}\parallel }_2^2& ={\int }_0^T{|x^{(n)}(t)|}^{2}dt\\ =\lambda \sum _{k=2}^{n+1}{\int }_0^T{F}_k(x^{(k-1)}(t))x^{\prime }(t)dt+\lambda {\int }_0^{T}g(t,x(t))x(t)dt+\lambda {\int }_0^{T}e(t)x(t)dt.\end{array}$$

Combining (2.2), (2.3), (2.8) and (2.9), we obtain

$$\begin{array}{rcl}{\parallel x^{(n)}\parallel }_2^2& =& {\int }_0^T{|x^{(n)}(t)|}^{2}dt\\ =& \lambda \sum _{k=2}^{n+1}{\int }_0^T[F_k(x^{(k-1)}(t))-F_k(0)]x^{\prime }(t)dt\\ +\lambda {\int }_0^T[g(t,x(t))-g(t,0)][x(t)-0]dt\\ +\lambda {\int }_0^{T}g(t,0)x(t)dt+\lambda {\int }_0^{T}e(t)x(t)dt\\ \le & \sum _{k=2}^{n+1}{L}_k{\int }_0^T|x^{(k-1)}(t)||x^{\prime }(t)|dt+|{\int }_0^{T}g(t,0)x(t)dt|\\ +|{\int }_0^{T}e(t)x(t)dt|+\lambda {\int }_0^T[g(t,x(t))-g(t,0)][x(t)-0]dt\\ \le & \sum _{k=2}^{n+1}{L}_k{\left({\int }_0^T{|x^{(k-1)}(t)|}^{2}dt\right)}^{\frac{1}{2}}{\left({\int }_0^T{|x^{\prime }(t)|}^{2}dt\right)}^{\frac{1}{2}}\\ +({\parallel e\parallel }_{\mathrm{\infty }}+{\parallel g(t,0)\parallel }_{\mathrm{\infty }})\frac{T^2\sqrt{T}}{4\pi }{\parallel x^{″}\parallel }_2\\ +({\parallel e\parallel }_{\mathrm{\infty }}+{\parallel g(t,0)\parallel }_{\mathrm{\infty }})Td+\lambda {\int }_0^T[g(t,x(t))-g(t,0)][x(t)-0]dt\\ \le & \sum _{k=2}^{n+1}{L}_k{\left(\frac{T}{2\pi }\right)}^{2n-k}{\parallel x^{(n)}\parallel }_2^2+({\parallel e\parallel }_{\mathrm{\infty }}+{\parallel g(t,0)\parallel }_{\mathrm{\infty }})\frac{T^2\sqrt{T}}{4\pi }{\left(\frac{T}{2\pi }\right)}^{n-2}{\parallel x^{(n)}\parallel }_2\\ +({\parallel e\parallel }_{\mathrm{\infty }}+{\parallel g(t,0)\parallel }_{\mathrm{\infty }})Td+\lambda {\int }_0^T[g(t,x(t))-g(t,0)][x(t)-0]dt.\end{array}$$

Now suppose that (S2) (or (S3)) holds, we will consider two cases as follows.

Case (i). If (S2) holds, then

$$\begin{array}{rcl}{\parallel x^{(n)}\parallel }_2^2& \le & \sum _{k=2}^{n+1}{L}_k{\left(\frac{T}{2\pi }\right)}^{2n-k}{\parallel x^{(n)}\parallel }_2^2+({\parallel e\parallel }_{\mathrm{\infty }}+{\parallel g(t,0)\parallel }_{\mathrm{\infty }})\frac{T^2\sqrt{T}}{4\pi }{\left(\frac{T}{2\pi }\right)}^{n-2}{\parallel x^{(n)}\parallel }_2\\ +({\parallel e\parallel }_{\mathrm{\infty }}+{\parallel g(t,0)\parallel }_{\mathrm{\infty }})Td,\end{array}$$

which implies that there exists a positive constant $C_n$ satisfying

$${\int }_0^T{|x^{(n)}(t)|}^{2}dt\le C_n\text{and}{\int }_0^T|x^{(n)}(t)|dt\le \sqrt{T{C}_n}.$$

(2.10)

Case (ii). If (S3) holds, (2.2) and (2.3) yield that

$$\begin{array}{rcl}{\parallel x^{(n)}\parallel }_2^2& =& {\int }_0^T{|x^{(n)}(t)|}^{2}dt\\ \le & \sum _{k=2}^{n+1}{L}_k{\left(\frac{T}{2\pi }\right)}^{2n-k}{\parallel x^{(n)}\parallel }_2^2+({\parallel e\parallel }_{\mathrm{\infty }}+{\parallel g(t,0)\parallel }_{\mathrm{\infty }})\frac{T^2\sqrt{T}}{4\pi }{\left(\frac{T}{2\pi }\right)}^{n-2}{\parallel x^{(n)}\parallel }_2\\ +({\parallel e\parallel }_{\mathrm{\infty }}+{\parallel g(t,0)\parallel }_{\mathrm{\infty }})Td+B{\int }_0^T{|x(t)|}^{2}dt\\ \le & \sum _{k=2}^{n+1}{L}_k{\left(\frac{T}{2\pi }\right)}^{2n-k}{\parallel x^{(n)}\parallel }_2^2+({\parallel e\parallel }_{\mathrm{\infty }}+{\parallel g(t,0)\parallel }_{\mathrm{\infty }})\frac{T^2\sqrt{T}}{4\pi }{\left(\frac{T}{2\pi }\right)}^{n-2}{\parallel x^{(n)}\parallel }_2\\ +({\parallel e\parallel }_{\mathrm{\infty }}+{\parallel g(t,0)\parallel }_{\mathrm{\infty }})Td+B{[\frac{T}{\pi }{\left(\frac{T}{2\pi }\right)}^{n-1}{\parallel x^{(n)}\parallel }_2+\sqrt{T}d]}^2\\ =& [\sum _{k=2}^{n+1}{L}_k{\left(\frac{T}{2\pi }\right)}^{2n-k}+B{\left(\frac{T}{\pi }\right)}^2{\left(\frac{T}{2\pi }\right)}^{2(n-1)}]{\parallel x^{(n)}\parallel }_2^2+[2Bd\frac{T\sqrt{T}}{\pi }{\left(\frac{T}{2\pi }\right)}^{n-1}\\ +({\parallel e\parallel }_{\mathrm{\infty }}+{\parallel g(t,0)\parallel }_{\mathrm{\infty }})\frac{T^2\sqrt{T}}{4\pi }{\left(\frac{T}{2\pi }\right)}^{n-2}]{\parallel x^{(n)}\parallel }_2\\ +({\parallel e\parallel }_{\mathrm{\infty }}+{\parallel g(t,0)\parallel }_{\mathrm{\infty }}+Bd)Td,\end{array}$$

which implies (2.10) holds.

Thus, from (2.2), (2.3), (2.4) and (2.10), we can choose a constant $C^{\ast }$ independent of λ and x such that

$${\parallel x^{(k)}\parallel }_{\mathrm{\infty }}\le C^{\ast },k=0,1,2,\dots ,n-1.$$

This completes the proof of Lemma 2.5. □

Lemma 2.6 Suppose that (S2) (or (S3)) hold, then (1.3) has at most one T-periodic solution.

Proof Suppose that $x_1(t)$ and $x_2(t)$ are two T-periodic solutions of (1.3). Set $Z(t)=x_1(t)-x_2(t)$. Then we obtain

(2.11)

Integrating (2.11) from 0 to T yields

$${\int }_0^T[g(t,x_1(t))-g(t,x_2(t))]dt=0.$$

Therefore, in view of the integral mean value theorem, it follows that there exists a constant $\gamma \in [0,T]$ such that

$$g(\gamma ,x_1(\gamma ))-g(\gamma ,x_2(\gamma ))=0.$$

From (S2) (or (S3)), we get

$$Z(\gamma )=x_1(\gamma )-x_2(\gamma )=0,$$

(2.12)

which together with (2.2) implies

$${\parallel Z\parallel }_2\le \frac{T}{\pi }{\parallel Z^{\prime }\parallel }_2.$$

(2.13)

Multiplying (2.11) by $Z(t)$ and integrating it from 0 to T, we obtain

$$\begin{array}{rcl}{\parallel Z^{(n)}\parallel }_2^2& =& {\int }_0^T{|Z^{(n)}(t)|}^{2}dt\\ =& \sum _{k=1}^{n+1}{\int }_0^T[F_k(x_1^{(k-1)}(t))-F_k(x_2^{(k-1)}(t))]Z^{\prime }(t)dt\\ +{\int }_0^T[g(t,x_1(t))-g(t,x_2(t))][x_1(t)-x_2(t)]dt.\end{array}$$

Now suppose that (S2) (or (S3)) holds, we will consider two cases as follows.

Case (i). If (S2) holds, (2.3) and (2.13) yield that

$$\begin{array}{rcl}{\parallel Z^{(n)}\parallel }_2^2& =& {\int }_0^T{|Z^{(n)}(t)|}^{2}dt\\ \le & \sum _{k=1}^{n+1}{L}_k{\int }_0^T|Z^{(k-1)}(t)||Z^{\prime }(t)|dt\\ \le & \sum _{k=1}^{n+1}{L}_k{\left({\int }_0^T{|Z^{(k-1)}(t)|}^{2}dt\right)}^{\frac{1}{2}}{\left({\int }_0^T{|Z^{\prime }(t)|}^{2}dt\right)}^{\frac{1}{2}}\\ \le & [L_1\frac{T}{\pi }{\left(\frac{T}{2\pi }\right)}^{2(n-1)}+\sum _{k=2}^{n+1}{L}_k{\left(\frac{T}{2\pi }\right)}^{2n-k}]{\parallel Z^{(n)}\parallel }_2^2,\end{array}$$

which together with (2.3) and (2.12) implies that

$$Z^{(n)}(t)\equiv Z^{(n-1)}(t)\equiv \cdots \equiv Z^{\prime }(t)\equiv Z(t)\equiv 0\text{for all }t\in R.$$

Hence, Eq. (1.3) has at most one T-periodic solution.

Case (ii). If (S3) holds, (2.3) and (2.13) yield that

$$\begin{array}{rcl}{\parallel Z^{(n)}\parallel }_2^2& =& {\int }_0^T{|Z^{(n)}(t)|}^{2}dt\\ \le & \sum _{k=1}^{n+1}{L}_k{\int }_0^T|Z^{(k-1)}(t)||Z^{\prime }(t)|dt+B{\int }_0^T{|Z(t)|}^{2}dt\\ \le & B{\left(\frac{T}{\pi }\right)}^2{\left(\frac{T}{2\pi }\right)}^{2(n-1)}{\int }_0^T{|Z^{(n)}(t)|}^{2}dt\\ +\sum _{k=1}^{n+1}{L}_k{\left({\int }_0^T{|Z^{(k-1)}(t)|}^{2}dt\right)}^{\frac{1}{2}}{\left({\int }_0^T{|Z^{\prime }(t)|}^{2}dt\right)}^{\frac{1}{2}}\\ \le & [L_1\frac{T}{\pi }{\left(\frac{T}{2\pi }\right)}^{2(n-1)}+\sum _{k=2}^{n+1}{L}_k{\left(\frac{T}{2\pi }\right)}^{2n-k}+B{\left(\frac{T}{\pi }\right)}^2{\left(\frac{T}{2\pi }\right)}^{2(n-1)}]{\parallel Z^{(n)}\parallel }_2^2,\end{array}$$

which together with (2.3) and (2.12) implies that

$$Z^{(n)}(t)\equiv Z^{(n-1)}(t)\equiv \cdots \equiv Z^{\prime }(t)\equiv Z(t)\equiv 0\text{for all }t\in R.$$

Therefore, Eq. (1.3) has at most one T-periodic solution. The proof of Lemma 2.6 is now completed. □

3 Main results

Theorem 3.1 Let (S1), (S2) (or (S3)) hold and let either $f_{n+1}(x)\equiv 0$ or $|f_{n+1}(x)|\ge {\alpha }^{\ast }>0$ for all $x\in R$, where ${\alpha }^{\ast }$ is constant. Then Eq. (1.3) has a unique T-periodic solution.

Proof From Lemma 2.6, we have obtained that Eq. (1.3) has at most one T-periodic solution. Thus, to prove Theorem 3.1, it suffices to show that Eq. (1.3) has at least one T-periodic solution. To do this, we will use Lemma 2.1. Firstly, let us show that (i) in Lemma 2.1 is satisfied, which means there exists $\rho >0$ such that any possible T-periodic solution x of (2.5) satisfies

$${\parallel x\parallel }_{(2n-1)}<\rho .$$

(3.1)

By Lemma 2.5, there exists $C^{\ast }>0$ such that any possible T-periodic solution x of (2.5) satisfies

$${\parallel x^{(k)}\parallel }_{\mathrm{\infty }}\le C^{\ast },k=0,1,2,\dots ,n-1.$$

If $f_{n+1}(x)\equiv 0$, from (2.5), (2.6) and (2.10), it follows that there exists a constant $C^{\ast \ast }$ satisfying

$${\int }_0^T|x^{(2n)}(t)|dt\le C^{\ast \ast },$$

(3.2)

which together with (2.4) implies the existence of a constant ρ, $\rho >d$ such that (3.1) holds.

If $|f_{n+1}(x)|>{\alpha }^{\ast }>0$, multiplying Eq. (2.5) by $x^{(n+1)}$ and integrating it from 0 to T, we obtain

$$\begin{array}{rcl}{\alpha }^{\ast }{\parallel x^{(n+1)}(t)\parallel }_2^2& =& {\alpha }^{\ast }{\int }_0^T{|x^{(n+1)}(t)|}^{2}dt\\ \le & \sum _{k=1}^n\underset{t\in [0,T]}{sup}|f_k(x^{(k-1)}(t)|{\int }_0^T|x^{(k)}(t)||x^{(n+1)}(t)|dt\\ +\underset{t\in [0,T]}{sup}\left|g(t,x(t))\right|{\int }_0^T|x^{(n+1)}(t)|dt+\underset{t\in [0,T]}{sup}|e(t)|{\int }_0^T|x^{(n+1)}(t)|dt\\ \le & \sum _{k=1}^n\underset{t\in [0,T]}{sup}|f_k(x^{(k-1)}(t)|{\left({\int }_0^T{|x^{(k)}(t)|}^{2}dt\right)}^{\frac{1}{2}}{\left({\int }_0^T{|x^{(n+1)}(t)|}^{2}dt\right)}^{\frac{1}{2}}\\ +{\parallel g\parallel }_{\mathrm{\infty }}\sqrt{T}{\left({\int }_0^T{|x^{(n+1)}(t)|}^{2}dt\right)}^{\frac{1}{2}}+{\parallel e\parallel }_{\mathrm{\infty }}\sqrt{T}{\left({\int }_0^T{|x^{(n+1)}(t)|}^{2}dt\right)}^{\frac{1}{2}}\\ \le & [\sum _{k=1}^n\underset{t\in [0,T]}{sup}|f_k(x^{(k-1)}(t)|{\parallel x^{(k)}\parallel }_2+{\parallel g\parallel }_{\mathrm{\infty }}\sqrt{T}+{\parallel e\parallel }_{\mathrm{\infty }}\sqrt{T}]{\parallel x^{(n+1)}(t)\parallel }_2.\end{array}$$

Therefore, there exists a positive constant $C_{n+1}$ satisfying

$${\int }_0^T{|x^{(n+1)}(t)|}^{2}dt\le C_{n+1},{\int }_0^T|x^{(n+1)}(t)|dt\le \sqrt{T{C}_{n+1}},$$

which together with (2.5), (2.6), (2.10) implies (3.2) holds. Thus, from (2.4) and (3.2), we can also show that (3.1) holds.

Now, to show that (ii) in Lemma 2.1 is satisfied, it suffices to remark that

$$F(x)={\int }_0^T[g(t,x)+e(t)]dt,x\in R.$$

Hence, from (S1) and $\rho >d$, it results that $F(-\rho )F(\rho )<0$. Then, by Lemma 2.1, we obtain that (1.3) has at least one T-periodic solution x satisfying ${\parallel x\parallel }_{(2n-1)}<\rho$. This completes the proof. □

4 An example

Example 4.1 Let $n=4$, $T=\pi$, $f_5(x)=sinx$, $f_k(x)=e^{\frac{1}{k}}cosx$, $k=1,2,3,4$, $g(t,x(t))=-e^{|sin4t|}{x}^3(t)$, $e(t)=\frac{1}{4}sin2t$. Then

$$x^{(8)}(t)+sin(x^{(4)}(t))x^{(5)}(t)+\sum _{k=1}^4{e}^{\frac{1}{k}}cos{x}^{(k-1)}(t)x^{(k)}(t)-e^{|sin4t|}{x}^3(t)=\frac{1}{4}sin2t$$

(4.1)

has a unique π-periodic solution.

Proof By (4.1), we have $n=4$, $L_5=1$, $L_k=e^{\frac{1}{k}}$, $k=1,2,3,4$, $T=\pi$, then

$$L_1\frac{T}{\pi }{\left(\frac{T}{2\pi }\right)}^{2(n-1)}+\sum _{k=2}^{n+1}{L}_k{\left(\frac{T}{2\pi }\right)}^{2n-k}<\frac{5}{8}<1.$$

It is obvious that the assumptions (S1), (S2) hold. Hence, by Theorem 3.1, (4.1) has a unique π-periodic solution. □

Example 4.2 Let $n=4$, $T=\pi$, $f_5(x)=sinx$, $f_k(x)=e^{\frac{1}{k}}cosx$, $k=1,2,3,4$, $g(t,x(t))=arctanx(t)$, $e(t)=\frac{1}{4}sin2t$. Then

$$x^{(8)}(t)+sin(x^{(4)}(t))x^{(5)}(t)+\sum _{k=1}^4{e}^{\frac{1}{k}}cos{x}^{(k-1)}(t)x^{(k)}(t)-arctanx(t)=\frac{1}{4}sin2t$$

(4.2)

has a unique π-periodic solution.

Proof By (4.2), we have $n=4$, $L_5=1$, $L_k=e^{\frac{1}{k}}$, $k=1,2,3,4$, $B=1$, $T=\pi$. Then

$$L_1\frac{T}{\pi }{\left(\frac{T}{2\pi }\right)}^{2(n-1)}+\sum _{k=2}^{n+1}{L}_k{\left(\frac{T}{2\pi }\right)}^{2n-k}+B{\left(\frac{T}{\pi }\right)}^2{\left(\frac{T}{2\pi }\right)}^{2(n-1)}<\frac{6}{8}<1.$$

It is obvious that the assumptions (S1), (S3) hold. Hence, by Theorem 3.1, (4.2) has a unique π-periodic solution. □

Remark 4.1 Obviously, the authors in [1–13] only considered the existence of periodic solutions of a high-order nonlinear differential equation. Although the author in [18] considered the existence and uniqueness of periodic solutions of high-order nonlinear differential equation, the coefficients of $x^{(k)}(t)$ are constants. Hence, the results obtained in [1–13, 18] and the references cited therein are not applicable to Examples 4.1-4.2. This implies that the results of this paper are essentially new.