Abstract
Interference signals in coherence scanning interferometry at high numerical apertures and narrow bandwidth illumination are spectrally broadened. This enables phase analysis within a spectral range much wider than the spectral distribution of the light emitted by the light source. Consequently, different surface features can be resolved depending on the wavelength used for phase analysis of the interference signals.
In addition, the surface topography itself affects the spectral composition of interference signals in different ways. Signals related to tilted surfaces or step height structures show special spectral characteristics. Thus, spectral amplitude and phase analysis enables a better understanding of the underlying physical mechanisms and gives hints how to improve the measurement accuracy.
Similar content being viewed by others
Introduction
White-light or coherence scanning interferometry (CSI) is one of the most used optical profiling techniques [1,2,3,4,5]. Proper application of CSI instruments assumes that their transfer characteristics are well-known. However, this is true only for phase analysis of CSI signals and surface height differences, which are much smaller than a quarter of the wavelength of the illuminating light [6]. Nonetheless, due to the ongoing miniaturization in micro- and nano-technology the lateral resolution capabilities and transfer characteristics close to the lateral resolution limit of CSI instruments become increasingly relevant.
The general assumption that the spectrum of a CSI signal from a mirror-like measuring object equals the spectrum emitted by the light source weighted by the spectral sensitivity of the camera is no longer fulfilled for high NA (numerical aperture) objective lenses. In particular, a 100x Mirau interferometer with a NA of 0.7 (Nikon CF IC Epi Plan DI) and a Linnik interferometer equipped with objective lenses of NA = 0.9 (Olympus MPLFLN100XBDP) used throughout this study show the well-known NA effect. This effect leads to an increased fringe spacing, which results in a longer effective wavelength of the measured correlograms [7,8,9,10].
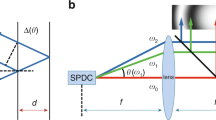
The phenomenon can be understood by the following consideration: The basic scheme of microscopic illumination known as Köhler illumination assumes an image of an extended incoherent light source in the pupil plane of the objective lens resulting in plane waves incident onto the surface of the measuring object under numerous angles [11]. The angular range spread out by these plane waves corresponds to the numerical aperture of the objective lens so that the maximum possible angle of incidence equals θmax = arcsin(NA) if the surrounding medium is air. Consequently, the higher the maximum angle of incidence, the better is the lateral resolution of the microscopic imaging. If the object under investigation is a grating with a period close to the diffraction limit of the CSI system the corresponding situation is outlined in Fig. 1. A plane wave characterized by the wave vector \( {\overrightarrow{k}}_{\mathrm{obj}} \) hits the object under the angle θe with respect to the optical axis. The zero order diffracted wave characterized by \( {\overrightarrow{k}}_r \) and the minus first order diffracted light characterized by \( {\overrightarrow{k}}_{\mathrm{diff}} \) enter the objective lens and therefore contribute to the microscopic image. If θe = θmax this leads to Abbe’s lateral resolution criterion of microscopic imaging [12]:
In the reference arm of the interferometer the wave characterized by the wave vector \( {\overrightarrow{k}}_{\mathrm{ref}} \) hits the reference mirror and the reflected wave propagates under an angle θe towards the objective lens (see Fig. 1b). During the depth scan the length of the measurement arm of the interferometer changes continuously and the resulting interference patterns are captured by the camera at certain positions of the so-called depth scanner, so that each camera pixel records an interference signal step by step.
However, with respect to the depth scan and the height structure of the measuring object only the z-component of the wave vectors contribute. The interference intensity for a certain point source in the pupil plane is thus given by:
where \( \widehat{z} \) is the unit vector in z-direction, z − z0 is the optical path length difference between measurement and reference arm of the interferometer, and γ(z − z0) is the temporal coherence function. For the second part of the above equation the relationships
hold. Consequently, an effective wavelength λeff instead of the center wavelength λ of the illuminating light represents the height difference corresponding to two bright fringes in the fringe pattern. In practice, not only a single point source has to be considered but the complete spatial distribution of light in the pupil plane of the objective lens [10]. However, for the sake of simplicity we confine the theoretical description to a single point source generating plane wave illumination on the object’s surface here.
As mentioned above, throughout this study we use a Mirau and a Linnik interferometer with numerical apertures of 0.7 and 0.9, respectively. Assuming the light source is a blue LED with a center wavelength of 460 nm, this results in a maximum effective wavelength of 644 nm for the Mirau and 1055 nm for the Linnik interferometer. This is the maximum wavelength contributing to the CSI signals and thus the maximum wavelength contribution in the spectrum of a measured CSI signal.
Figure 2 confirms these considerations. Figure 2a shows spectra of simulated CSI signals assuming NA values of 0.14, and 0.9, respectively. For comparison the spectrum of the light source assumed for the simulation is plotted. The simulation model is based on a Kirchhoff approach and results in interference signals, which are analyzed with signal processing algorithms that are also used for experimental data [13, 14]. As demonstrated by Fig. 2 the absolute value of the Fourier transform of such signals shows that additional low frequency (long wavelength) contributions occur at high NA. These are attributed to oblique angles of incidence and appear even if a narrow band light source is used [15, 16]. For this reason the corresponding effect in the spatial domain is related to the longitudinal spatial coherence [16].
Figure 2b) depicts spectral distributions of CSI signals (i. e. the absolute values of the spectral coefficients calculated by discrete Fourier transformation) obtained with interferometers of different NA. The effect of spectral broadening clearly turns out. For NA = 0.9 wavelength contributions of more than 900 nm occur, for NA = 0.7 a maximum wavelength of more than 600 nm appears, and for NA = 0.55 the spectrum extends up to more than 500 nm.
In an earlier paper we documented the dependence of the lateral resolution of a phase measuring interference microscope on the so-called evaluation wavelength λeval, which is the wavelength that is used for phase analysis [15].
In addition, local surface features such as height steps, slopes, or curvatures of the surface of the measuring object affect the shape of the spectrum of interference signals [9, 13, 14]. This represents a potential source of measurement errors, which must be taken into account the more the measuring object differs from an optical flat.
In this context, it should be noted that the Fourier transform of the envelope of an interference signal is often interpreted as its spectral distribution centered at the central frequency of the interference signal [17]. Consequently, spectral changes primarily affect the shape of the envelope and measurement errors occur if the maximum position of the envelope is used for height determination. For this reason, phase analysis behaves more robust and thus we only discuss results of phase analysis of CSI signals in the following sections.
Methods
For our experimental investigations we used a pitch standard manufactured by the company Supracon AG in order to show the relationship between the evaluation wavelength and the corresponding spatial frequency of the almost rectangular surface structures [18]. The standard provides grating structures of 0.3 and 0.4 μm period and 25 nm depth, etched in a nanocrystalline silicon layer on a quartz substrate. These periods are close to the lateral resolution limit of 0.33 μm for the Mirau interferometer and 0.26 μm for the Linnik system. The resulting interference patterns are phase analyzed pixel by pixel using three different evaluation wavelengths. Results are discussed for the nominal wavelength of the light source (460 nm for the blue LED), the center wavelength of the interference signal (520 nm for the Mirau and 600 nm for the Linnik interferometer) occurring on a flat mirror, and longer wavelengths (650 nm for the Mirau and 800 nm for the Linnik system) corresponding to higher angles of incidence.
A piezo z-stage moves the pitch standard along the optical axis (z-axis) of the interferometer while a camera takes an image every 20 nm. The wavelength dependent spectral composition of CSI signals at steep edges will be demonstrated by use of the RS-N standard manufactured by Simetrics GmbH comprising a rectangular grating of 6 μm period with perpendicular edges and a nominal groove depth of 190 nm [19]. CSI measurements obtained with a Mirau system of NA = 0.55 under red and blue LED illumination will be compared.
Finally, measurements performed with the Linnik interferometer on a mirror tilted more or less with respect to the optical axis further affect the composition of CSI signal spectra. Figure 3 displays a scheme of the physical situation. If the object’s surface is perfectly aligned as shown in Fig. 3a) the incident light cone and the reflected light cone will spread over the same angular range. However, if the object’s surface is tilted according to Fig. 3b) the reflected light cone will be tilted too, and only the light in the overlapping section of these two cones will contribute to the measured interference signals.
In order to detect the phase of a CSI-signal for a certain evaluation wavelength we use a lock-in algorithm [20, 21].
Results and discussion
Figures 4, 5 and 6 demonstrate the relationship between spatial frequency of the surface structure and evaluation wavelength of the corresponding CSI signals. In Fig. 4a) the 0.4 μm structure is hardly resolved with the Mirau interferometer assuming the smallest evaluation wavelength of 460 nm. However, the low frequency structure in the surrounding of the measured grating is resolved. Increasing the evaluation wavelength increases the measured groove depth of the grating structure and, therefore, improves the lateral resolution of the topography measurement. However, the maximum evaluation wavelength, for which significant spectral contributions occur, is limited to approximately 600 nm here. Even at λeval = 600 nm the surface profile looks quite noisy due to the rather low intensity value at this wavelength for a numerical aperture of 0.7 (see Fig. 2b).
Higher evaluation wavelengths providing better lateral resolution are accessible with the Linnik interferometer as displayed in Figs. 5 and 6.
Figure 5a and d show that an evaluation wavelength of 460 nm will not resolve the 0.3 μm grating structure, but the surrounding structures of lower spatial frequency are quite well resolved. At λeval = 600 nm (Fig. 5b and e) the amplitude of the low-frequency structure at the left and right hand side of the profile is reduced but the high frequency structure is still not resolved. Using an evaluation wavelength of 800 nm resolves the high frequency grating structure but the low-frequency contributions become blurred.
The results according to Fig. 6 are obtained with the Linnik system from the 0.4 μm grating structure and confirm that the height steps in the surrounding of the grating structure are most accurately reproduced if 460 nm is used as the evaluation wavelength. In contrast, the best result for the grating structure appears at 600 nm evaluation wavelength, whereas for an evaluation wavelength of 800 nm the measured grating topography deteriorates again. This has to do with the discrepancies of the angle of incidence θe resulting from the choice of the evaluation wavelength
and the angle θdiff corresponding to the first diffraction order of the reflection grating:
where Λ is the grating period. For λ = 460 nm (blue LED) the angle θe = 40° corresponds to λeval = 600 nm. For λeval = 800 nm an angle θe = 55° results. The first order diffraction angle is 35° for Λ = 0.4 μm and 50° for Λ = 0.3 μm. With respect to Fig. 6b and e the angle corresponding to the evaluation wavelength and the diffraction angle are closest to each other (Λ = 0.4 μm, θdiff = 35°, θe = 40°). This explains the good resolution of the grating structure in this case.
Comparison of Figs. 4d and 6d) shows that the same structure in the surrounding of the grating looks somehow low-pass filtered in the result of the Mirau interferometer. We suppose that this is a consequence of the obscuration of the reference mirror in the Mirau system, which prevents light rays from striking the object or the reference mirror surface perpendicularly.
Figure 7 considers the overshooting phenomenon at edges called batwing effect [22], which has been subject to prior publications of our group [14, 23]. Figure 7a and b show measured profiles of the rectangular grating structure of the RS-N standard obtained with a Mirau system (NA = 0.55). If the illumination wavelength is changed from 628 nm (red LED) to 444 nm (blue LED) the batwings disappear. This is a consequence of the height to wavelength ratio (HWR) as pointed out in ref. [14]. Due to the NA effect the wavelength, which is relevant with respect to the HWR, is the effective wavelength. Hence, the HWR is close to 0.25 for the red LED. Therefore, in this case destructive interference occurs at the edges, leading to strong batwings if the measured profile is taken from the maximum positions of the envelopes of the CSI signals. If the batwing height exceeds a quarter of the evaluation wavelength used for phase analysis, the fringe order will no longer be determined correctly and thus phase jumps appear. Using a blue LED increases the HWR significantly so that the batwings reduce. In the ideal case of HWR = 0.5 the light diffracted from the upper and lower edge of a height step will interfere constructively and batwings will be eliminated. The spectra according to Fig. 7c reveal the consequences of destructive interference at the edges: the corresponding spectra are strongly distorted whereas for the blue LED illumination according to Fig. 7d the spectra at the edges are characterized by the same shape compared to the spectra corresponding to flat surface plateaus [13, 14].
Profiles of a rectangular grating standard (RS-N with 6 μm period manufactured by Simetrics) obtained by a Mirau interferometer with NA = 0.55 using (a) red and (b) blue LED illumination with center wavelength of 628 nm and 444 nm, respectively, (c) and (d) corresponding signal spectra for pixels related to edges and plateaus
Finally, Fig. 8 depicts the consequences of surface tilt. The profiles of a flat mirror shown in Fig. 8a become more and more noisy as the surface tilt angle increases. However, even if the tilt angle is 59°, which is close to the maximum tilt angle of 64° according to the numerical aperture of the Linnik system, the linear course of the profile can be recognized. Due to the decreasing overlap of the two light cones according to Fig. 3b the light intensity plotted in Fig. 8b will decrease too if the tilt angle increases. Furthermore, with an increasing tilt angle the angles of incidence and reflection increase as well as the effective wavelength of light. Therefore, the spectral distributions will shift to lower spatial frequencies as Fig. 8b reveals. This effect needs to be considered if surface structures with strong local tilt are to be measured. One has to keep in mind that meaningful results only occur at those spatial frequencies or wavelengths, for which the spectral contribution of the corresponding interference signal significantly differs from zero.
If the center wavelength of a CSI signal for a perfectly aligned surface, which is perpendicular to the optical axis, is chosen as evaluation wavelength a strong loss of signal intensity occurs at high surface tilts and, therefore, the maximum measurable tilt angle of a surface structure is typically much smaller than the angle θmax.
Conclusions
This contribution deals with the analysis of physical phenomena, which affect the spectral distribution of CSI signals and thus may reduce or enhance the accuracy of CSI measurements.
The low frequency or long wavelength contributions up to wavelengths of more than 900 nm occurring at a NA of 0.9 even in the case of blue LED illumination correspond to oblique angles of incidence. Thus, phase analysis at long evaluation wavelengths corresponding to long effective wavelengths enable high lateral resolution according to Abbe’s theory of microscopic imaging. As we demonstrate by example of a pitch standard providing line gratings with periods of 0.3 and 0.4 μm, phase analysis of interference signals at longer evaluation wavelength enable improved lateral resolution of the optical topography measurement. At first glance this seems to contradict the fact that better lateral resolution can be achieved by reducing the wavelength of light [12]. However, the wavelength we discuss here is the effective or evaluation wavelength, which results from higher NA and oblique incidence and corresponds to lower spatial frequency contributions occurring if the NA increases while the central wavelength of the used light source remains unchanged.
Moreover, our experimental results suggest that phase analysis of a CSI signal at a certain wavelength seems to comprise a kind of bandpass filtering, where only certain spatial frequency contributions of a measured surface structure will contribute to the measured surface profile.
It should be noted that the spatial frequency dependent analysis of measurement data is a unique opportunity due to the interferometric measurement, which in contrast to other optical profiling techniques such as confocal of focus scanning microscopy enables wavelength dependent signal processing.
With respect to height steps the spectral distribution of CSI signals occurring at an edge allows to adjust the center wavelength of the illuminating light in a way that artefacts such as batwings will be minimized.
Finally, steeper surface slopes lead to CSI signal spectra, which are shifted to higher wavelength, i. e. higher angles of incidence compared to signals obtained from perfectly adjusted mirror-like surfaces. For this reason care must be taken if steeper surface slopes are to be measured, since phase analysis will only lead to robust measurement results as long as there is enough signal power in the spectrum of a CSI signal at the chosen evaluation wavelength.
References
Kino, G.S., Chim, S.S.C.: Mirau correlation microscope. Appl. Opt. 29, 3775–3783 (1990). https://doi.org/10.1364/AO.29.003775
Lee, B.S., Strand, T.C.: Profilometry with a coherence scanning microscope. Appl. Opt. 29, 3784–3788 (1990). https://doi.org/10.1364/AO.29.003784
Caber, P.J.: Interferometric profiler for rough surfaces. Appl. Opt. 32, 3438–3441 (1993). https://doi.org/10.1364/AO.32.003438
Malacara, D.: Optical Shop Testing. Wiley, Hoboken, New Jersey, USA (2007)
de Groot, P.: Principles of interference microscopy for the measurement of surface topography. Adv. Opt. Photon. 7, 1–65 (2015). https://doi.org/10.1364/AOP.7.000001
de Groot, P., de Lega, X.C.: Interpreting interferometric height measurements using the instrument transfer function. Proc. Fringe. 2005, 30–37 (2005)
Tolmon, F.R., Wood, J.G.: Fringe spacing in interference microscopes. J. Scientific Instruments. 33, 236–239 (1956)
Biegen, J.F.: Calibration requirements for Mirau and Linnik microscope interferometers. Appl. Opt. 28, 1972–1974 (1989). https://doi.org/10.1364/AO.28.001972
Creath, K.: Calibration of numerical aperture effects in interferometric microscope objectives. Appl. Opt. 28, 3333–3338 (1989). https://doi.org/10.1364/AO.28.003333
Sheppard, C.J.R., Larkin, K.G.: Effect of numerical aperture on interference fringe spacing. Appl. Opt. 34, 4731–4734 (1995). https://doi.org/10.1364/AO.34.004731
Köhler, A.: Ein neues Beleuchtungsverfahren für mikrophotographische Zwecke. Zeitschrift für wissenschaftliche Mikroskopie und für Mikroskopische Technik. 10(4), 433–440 (1893)
Abbe, E.: Beiträge zur Theorie des Mikroskops und der mikroskopischen Wahrnehmung. Archiv für mikroskopische Anatomie. 9(1), 413–468 (1873)
Lehmann, P., Xie, W.: Signal formation in depth-scanning 3D interference microscopy at high numerical apertures. SPIE Proc. 9660, 966015 (2015). https://doi.org/10.1117/12.2197635
Xie, W., Lehmann, P., Niehues, J., Tereschenko, S.: Signal modeling in low coherence interference microscopy on example of rectangular grating. Opt. Exp. 24, 14283–14300 (2016). https://doi.org/10.1364/OE.24.014283
Lehmann, P., Xie, W., Allendorf, B., Tereschenko, S.: Coherence scanning and phase imaging optical interference microscopy at the lateral resolution limit. Opt. Exp. 26, 7376–7389 (2018). https://doi.org/10.1364/OE.26.007376
Abdulhalim, I.: Spatial and temporal coherence effects in interference microscopy and full-field optical coherence tomography. Ann. Phys. 525, 787–804 (2012). https://doi.org/10.1002/andp.201200106
Buchta, Z., Mikel, B., Lazar, J., Cip, O.: White-light fringe detection based on a novel light source and colour CCD camera. Meas. Sci. Technol. 22, 094031 (2011). https://doi.org/10.1088/0957-0233/22/9/094031
Homepage Supracon AG. http://www.supracon.com/en/nanoscale_linewidth_pitch_standard.html. Accessed 20 Mar 2019
Homepage Simetrics GmbH. http://www.simetrics.de/en/produkte.html. Accessed 20 Mar 2019
Fleischer, M., Windecker, R., Tiziani, H.J.: Fast algorithms for data reduction in modern optical three-dimensional profile measurement systems with MMX technology. Appl. Opt. 39, 1290–1297 (2000). https://doi.org/10.1364/AO.39.001290
Tereschenko, S.: Digitale Analyse periodischer und transienter Messsignale anhand von Beispielen aus der optischen Präzisionsmesstechnik, PhD Thesis. University of Kassel, Kassel (2018)
Harasaki, A., Wyant, J.C.: Fringe modulation skewing effect in white-light vertical scanning interferometry. Appl. Opt. 39, 2101–2106 (2000). https://doi.org/10.1364/AO.39.002101
Xie, W., Lehmann, P., Niehues, J.: Lateral resolution and transfer characteristics of vertical scanning white-light interferometers. Appl. Opt. 51, 1795–1803 (2012)
Acknowledgements
The authors gratefully acknowledge the funding of parts of this work by the German Research Foundation.
Funding
Partially by the German Research Foundation, projects LE 992/6–2 and LE 992/15–1.
Availability of data and materials
As given in the present paper.
Author information
Authors and Affiliations
Contributions
All authors contributed to this work. PL analysed and simulated the occurring effects, interpreted the data and wrote the manuscript, ST wrote the measurement and data evaluation programs, BA performed the measurements according to Fig. 8, SH obtained the measurement results shown in Figs. 2b, 4 and 7, and LH obtained the measurement results shown in Figs. 5 and 6. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Authors’ information
As given in the present paper.
Competing interests
The authors declare that they have no competing interests.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lehmann, P., Tereschenko, S., Allendorf, B. et al. Spectral composition of low-coherence interferograms at high numerical apertures. J. Eur. Opt. Soc.-Rapid Publ. 15, 5 (2019). https://doi.org/10.1186/s41476-019-0101-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s41476-019-0101-8