Abstract
Active microfluidics for the applications to cellular deformability measurements is an emerging research field ranging from engineering to medicine. Here, we review conventional and microfluidic methods, and introduce an on-chip cell manipulation system with the design principle of fast and fine cell manipulation inside a microchannel. In the latter part of the review, we focus on the results of red blood cell (RBC) deformability measurements as one of the most frequently studied non-adherent cells by on-chip methods. The relationship between mechanical properties and biological structures/features, as well as medical/diagnostic applications, are also discussed.
Similar content being viewed by others
Introduction
Applications of the biological mechanics to the engineering issues has been one of the frontier topics in the research fields of mechatronics and robotics. Living organisms are flexible in shapes and accurately functionalized in association with the sophisticated structures and metabolic energies generated by consuming adenosine triphosphate (ATP). The minimum, microscopic component of the living organisms is a single cell. Even in the single-cell level, cells exhibit typical functions such as energy transductions, motility in response to the stimuli, adaptation of the shapes and internal states to the surrounding environment, and replication of themselves [1]. Considering that typical cells are under a microscopic aqueous environment, it is surprising that they precisely control these functions using tiny molecular machineries against thermal fluctuations.
Cellular deformability is essentially important to realize the various cellular functions. In the viewpoint of the mechanical properties, the cells exhibit both elasticity and viscosity, which exert restoring forces to their original undeformed shapes and frictional forces against the shape changes, respectively. The typical elasticity (Young’s modulus) of a cell is on the orders of Pa–kPa, and the corresponding typical force range for cellular deformation is on the order of piconewton [2]. Owing to the deformability, the mechanical aspects of the cells can be classified into “soft materials”.
Typical assays for the analyses and evaluations of biological materials are performed in a petri dish or a microwell plate under a microscope. According to the developments of the experimental techniques to treat such small and soft objects, various methods have been invented to quantify the mechanical properties of a single cell. Conventional methods for measuring the cell mechanics are, for example, atomic force microscopy (AFM) [3,4,5,6], optical tweezers [7, 8], magnetic forces [9,10,11], fluctuating spectrum analysis (flicker spectroscopy) [12,13,14], and particle-tracking microrheology [15,16,17,18], which will be explained later in detail. During the last two decades, microfluidic devices and the related experimental techniques have also been intensively developed along with the maturation of nanoscopic and microscopic fabrication technologies. Recently, the microfluidic techniques have been utilized as fundamental experimental tools to treat small amount of fluids, molecules, particles, and cells in the vast research topics in robotics, mechatronics, science, pharmacy, and medicine. All of above-mentioned measurement methods have both advantages and disadvantages, e.g., AFM provides rich viscoelastic information based on nanoscopic probe deflection but takes much long time to perform the measurements. In contrast, the microfluidic devices enable high-throughput measurements but provide less information such as the aspect ratio of the deformed shape, which has no information with physical units. In a similar manner, each method is developed under the trade-off relationship between the throughput and information content [19].
In this review, we describe recent developments of microfluidic technology for measuring cellular mechanics, and also recent efforts for overcoming the trade-off between the throughput and information content. In the following, we first review the conventional methods for the measurements of cellular mechanical properties. Next, the microfluidic techniques are reviewed from the viewpoint of the methods with passive flow and with actively controlled flow. In particular, we explain the details of the active control techniques, where we can impose controlled mechanical stress to a single cell through the integration of an actuator and a high-speed vision into the microfluidic platform, called an on-chip manipulation system. We describe the design principles for the fast and fine cell manipulation inside a microchip, and show how such interdisciplinary collaboration between mechanical engineering and biological materials reveals novel aspects of cell mechanics. In addition, we discuss the relationship between the obtained mechanical characteristics and the biological structures. Finally, toward medical applications, we remark potential diagnoses of diseased cells with case examples.
Measurement methods of cellular mechanical properties
In this section, we review conventional methods for measuring the cellular mechanical properties. Figure 1 shows the schematics for the typical conventional methods, while the actual devices and experimental setups for these measurements highly depend on the cases. To measure the elasticity and/or viscosity of a microscopic material, in general, either a sensitive force sensor or a sensitive displacement sensor is necessary. Namely, we have to apply a precisely controlled small force and measure the corresponding small displacement, or have to apply a precisely controlled small displacement and measure the corresponding small reaction force. From the measured dynamic stress-strain relationship, viscoelastic coefficients are obtained. Since different types of the measurement methods have different spatial resolutions, time resolutions, throughput, advantages, and disadvantages, a variety of studies with various setups and equipment have revealed the different aspects of the cellular mechanical properties.
In AFM measurements of a microscopic soft materials, the small, sensitive probe is a cantilever, whose nanoscopic deviation can be detected by laser beam deflection. Figure 1a shows a schematic illustration of the measurement principle of AFM. Viscoelasticity measurement by AFM is performed by applying a known indentation pattern to the sample and detecting the cantilever deflection, which reflects the reaction force. The amplitude of the deflection and the delayed responses provide the elastic and viscous information, respectively. By scanning over the sample surfaces, two-dimensional viscoelasticity maps are obtained. Whereas the outputs of an AFM measurement contain full information of viscoelastic coefficients with high spatial resolution (~ nm), the typical throughput is low (~ 10−3 Hz) since the setup and scanning are time-consuming [2, 19, 20]. In addition, only nanoscopic viscoelasticity is accessible since the applied deviation by a cantilever is localized in a nanoscopic length scale.
In the methods with optical or magnetic tweezers, the probe is a small particle attached onto the cell surface. Figure 1b, c show schematic illustrations of the manipulation of a particle attached onto the surface of a single cell by optical and magnetic tweezers, respectively. In the case of optical tweezers, the particles are typically made of silica or polystyrene with high refractive index, and manipulated by radiation pressure of a focused laser beam. From the displacement of the particle from the focused center and spring constant of the trap force obtained in calibration setup, the particle displacement and the restoring force are quantified, resulting in the viscoelastic coefficients. The basic concept is the same in the methods with magnetic tweezers and other types of methods with magnetic fields. In those cases, the magnetic particles are used and manipulated by an external magnetic field. These methods also provide the viscoelastic coefficients with a good spatial resolution (~ µm), and the throughput is better than AFM (~ 10−1–10−2 Hz) [2, 19, 20]. If the tracer particles are injected into the cytosol rather than attached onto the cell surface, these methods are often called particle-tracking microrheology.
For the measurement of cytosolic viscoelastic properties, particle-tracking passive microrheology is another typical class, which utilizes the thermal fluctuation as a force probe. Figure 1d shows the representative image for the particle-tracking microrheology. By measuring the thermal deviation of a tracer particle under constant temperature condition, the viscosity of the surrounding medium can be estimated through fluctuation-dissipation theorem [21]. In the similar principle, shape-fluctuation analysis, conventionally termed as flicker spectroscopy, has been also developed since 1975 [12] to evaluate the membrane bending rigidity, surface tension, and viscosity [13]. Since the typical thermal energy under room temperature is small as ~ 4 × 10−21 J, this method is applicable only to extremely soft objects such as red blood cell (RBC) with Young’s modulus of the order of tens of Pa [7, 22]. The remarkable advantage of the shape-fluctuation analysis is non-invasiveness; all we need in the experiment is to observe the thermal fluctuation under a resting state. The spatial resolution is in the optical limitation (~ µm) and the throughput is intermediate (~ 10−1–10−2 Hz), which are comparable to the particle-tracking methods.
In the last part of this section, we mention the micromanipulation techniques such as micropipette aspiration [22,23,24] or object handlings by microneedles [25], microknives [26], and microhands [27,28,29,30]. For more details of the nano/microrobots for the single cell analyses, see a comprehensive review [31]. Figure 1e shows the schematic image of the micropipette aspiration. The micromanipulation techniques are usually adopted for microinjection experiments, where a single cell is held by capillary suction and reagents are injected into the cytosolic part through another capillary. In the micromanipulation, the cells are directly contacted by a probe, a microneedle, a microknife, or a microcapillary, under a microscope. The probe is controlled by a macroscopic actuator called a micromanipulator. Micropipette aspiration has been intensively used for evaluation of cellular surface tension through the measurement of the negative pressure to keep the suction length. While the spatial resolution is in the size of a single cell, i.e., 1–10 µm, information content is relatively less compared to AFM [2, 19, 20]. The throughput is at the similar level to that of AFM, because the micromanipulation also needs the careful handling of a cell one by one under a microscope. Recent studies have developed the micropipette aspiration toward automation [32]. Recent developments of microhands are also remarkable; microhands and/or microfingers that are realized by actuating several needles simultaneously by piezo electric devices are being developed [27,28,29,30].
Passive flow in microfluidics
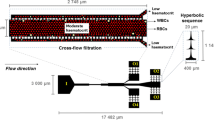
Along with the improvements in nano/microfabrication and developments of the research field of Micro Electro Mechanical Systems (MEMS), microfluidic techniques have been utilized to measure the cellular mechanical properties. The microfluidic approaches greatly increase the throughput compared to the conventional ones [19]. A typical microfluidic method for the measurement of single-cell mechanics is to evaluate the shape deformation under a shear flow in a microchannel. This strategy is advantageous to the throughput (typically 103–104 cells per second), the reduction of sample volumes (typically less than 1 mL), as well as integration of other processes such as size sorting. RBCs are one of the most successful and intensively studied subjects in the history of this field, as their physiological situation, flowing in a narrow blood vessel [33, 34], can be mimicked as the flow in a microfluidic channel. In the same reason, other types of non-adherent cells such as other blood cells [35, 36] and other eukaryotic cells such as circulating tumor cells (CTCs) [37, 38] are also suitable for the microfluidic experiments.
For the applications to the measurement of RBC mechanics, Brody et al. reported the deformability test performed in a microchannel fabricated by the semiconductor processing techniques [39]. They observed the characteristic folded shape (like “hot-dog bun”) of a deformed RBC when it passed through the 4 µm width channel, and measured the passing speeds for various channel widths. The large dispersion of the data was interpreted to the heterogeneity among the individual RBCs. From the second half of 2000, many groups have started to report the microfluidic measurements of single-RBC mechanics. Most popular strategy was the quantification of the passage through a narrow channel under a constant pressure difference between the inlet and the outlet as shown in Fig. 2 [40,41,42,43,44,45]. Note that the widths of the narrow channels used here were comparable or less than the size of a single cell to confine the degree of freedom of the cell motion to one-dimensional line for the simple and defined experimental situations. In this context, various biological and mechanical aspects have been quantified: ATP-release under wall shear stress [46], passing velocity through the narrow part [43] and the channel-width dependence [45], aspect ratio [47], circularity [48, 49], elastic constants [49,50,51], and viscoelastic recovery time [52]. In those studies, RBCs exhibit stiffness (shear modulus) of the order of 10−6 N/m, time constant of the order of 0.1 s for shape recovery, and large dispersions of the measured values as their typical mechanical responses. As the nonlinear responses, the stiffness is increased with higher strain rate [50] or with a longer storage period [51], and the shape recovery time is typically reduced under ATP depletion [52]. Since different stress conditions induce different types of deformation, the various studies have revealed different aspects of the cellular deformability, e.g., two different orders of shape recovery time have been observed for combined twisting and folding deformation [52]. While the passive microfluidics has been highly successful in these two decades, it has suffered from less information content in the output of the experiment compared to the those in the conventional methods. The disadvantages in passive microfluidics mainly come from the trade-off accuracy against high throughput. Also, the small and closed space in a microfluidic channel has limited the evaluation methods, typically only to the shape visualization by a high-speed camera. For the precise evaluation of the detailed mechanical properties, active control of the experimental parameters is necessary. In this context, researchers have developed on-chip manipulation systems shown in the following section.
Active control in microfluidics
The protocols for the active control of the experimental parameters, namely, precise applications of a specified stress or deviation to a single cell in a microchannel, have been recently developed. In this review, we call this technique “on-chip cell manipulation”. To realize the on-chip cell manipulation, the two mechatronics components should be equipped: an actuator to drive the cell motion and a sensor for tracking the cell position or state.
As for the actuator equipped on a microchannel, both microscopic and macroscopic actuators have been used. Here, the terms microscopic and macroscopic mean the length scales for a single cell and a macroscopic tube or syringe, respectively. Microactuators and macroactuators have both advantages and disadvantages from the viewpoint of the on-chip cell manipulation. Let us suppose the typical situation of a single-line microchannel shown in Fig. 3. In the case of a microactuator, the spatial resolution of the cell motion is the same as that of the actuator, which is advantageous for the simple, fine manipulation. However, the fabrication cost is high, and the microchip including the microactuator should be discarded once the channel clogging happens. In the case of the macroactuator, on the other hand, the microchip itself contains no expensive parts, and is cheap and disposable. Thus, the clogged microchip is easily replaced by a clean one with very low cost. However, the spatial resolution of the cell motion is much low due to the huge cross-sectional-area ratio of the actuator to the microchannel. The typical ratio is over one million, which results in the loss of fine manipulation due to the million-times increase in the deviation and the velocity. Sakuma and the coauthors discussed the velocity-increase issue and proposed a possible solution called “virtual reduction gear” as schematically shown in Fig. 4 [53]. The virtual reduction gear is a macroscopic elastic part whose spring constant is represented by k. For incompressible fluid, the volume conservation and the force balances for the target cell and the elastic part are given by
where Ai is the cross-sectional area for the i-th part [i = 1 (macroactuator), 2 (target cell), and 3 (elastic part)], δi is the displacement for the i-th part, and c is the frictional coefficient of the flowing target cell. Here, even under high pressure, the microfluidic flow is a laminar flow due to the large shear stress from the wall, and therefore, the pressure is constant during the sampling interval. These equations can be solved under the constant-pressure assumption and the initial condition δ2(t = 0) = 0 under the step input of the deviation δ1 at t = 0 as

(The figure is taken from [53] (reproduced under CC BY-NC-SA 4.0, see the reference for details))
Simple model for a the macroactuator system and b the system with “virtual reduction gear”
If we consider the motion of the target cell at the initial stage (\(t \approx 0\)), which is within a single sampling step \(\Delta t \approx 0\), the initial response of the target cell reads
In this regime, the reduction ratio between the motions of the actuator and the target cell can be defined as \(\delta_{2} /\delta_{1}\) and thus
is obtained. The positioning resolution is improved if the right-hand side is less than 1, and it is the case of the macroscopic actuator. For example, a piezo electric actuator is a commercially available macroactuator, whose cross-sectional diameter is on the orders of mm and produce a high-frequency characteristic of 10 kHz. If the piezo electric actuator is connected to a microchannel with a cross-sectional diameter of 10 µm, the factor of (A2/A3)2 becomes 10−10, indicating the drastic reduction effect of the deviation, i.e., the drastic improvement in the positioning resolution.
Even though the theoretical evaluation is 1 m without the virtual reduction gear, we could confirm a high positioning resolution of 240 nm in our experimental system composed of a piezoelectric actuator driven in Δt of the order of ms and a PDMS microchip with a microchannel of 10 µm width, where the wide inlet area for tubing plays a role of the virtual reduction gear [53]. Note that the 240 nm is a pixel resolution of the vision system, which is the bottle-neck of the positioning resolution worse than the theoretical value derived above. Figure 5 shows an example of open-loop frequency characteristics of the on-chip manipulation system [54], where the gain characteristics shows a typical integral form, and the phase characteristics shows 180° delay under the frequency of 100 Hz. This frequency characteristics confirms the first order system under the position-feedback loop. In general, while the integral-formed open-loop characteristics can keep stable behaviors even in high frequencies, the delay in the system can cause the instability in that frequency region. A key remark on the on-chip cell manipulation by using a microfluidic channel is that a fast and fine manipulation can be achieved by combining a macroactuator and a reduction system to drive the flow inside a microfluidic channel.

(The figure is taken from [54] (reproduced under CC BY-NC-SA 4.0, see the reference for details))
Example of frequency characteristics of the on-chip cell manipulation system
Developments of this on-chip manipulation system and the evaluations of the characteristic mechanical properties of RBCs have been performed mainly by the authors’ group. Sakuma and the coauthors performed fatigue test, where a RBC was manipulated to pass through a narrow constriction repeatedly over 1000 times at ~ 1 Hz, and the number of passage until the loss of its extensibility and recoverability was used for the index of deformability [55]. Such long-time loading applied inside a microfluidic channel was the first attempt in this field. Ito and coauthors have further investigated the effect of long-time loading to a RBC and/or an eukaryotic cell, which exhibit a nonlinear mechanical response against different loading time [56,57,58,59]. Here, the combination of the high-speed feedback control of the cell position and the geometrical constriction worked like a microfluidic hand, and the cell shape was kept folded and elongated for a desired time period. These techniques enabled the on-chip quantification of the cellular viscous information, where the control of the deformation time is required. This point is the qualitative difference from passive microfluidic techniques, where the cells rapidly flow out of the view under a constant driving pressure. As a result of the loading-time dependence, the shape recovery of a RBC after loading became slower with the increase in the loading time [57]. Similar behaviors were observed also in a fibroblast cell, a kind of eukaryotic cell [59]. Assuming a viscoelasticity composed of linear springs and dampers, the shape recovery time does not depend on the loading time in theory. In contrast, the experimentally measured values exhibited strong dependence on the loading time as well as the amount of ATP. The discrepancy to the linear viscoelasticity theory and the ATP-dependence should reflect special internal structures of the cell, which will be discussed in the next section.
In the on-chip manipulation system, the deformability measurement is performed only with photographs taken from a high-speed camera, displacement of a piezo electric actuator, and microstructures in a microchannel; no force sensor is equipped. Therefore, the typical output is deformability index (aspect ratio) [55] or the ratios between mechanical parameters [57]. In other words, the physical unit of force “N” lacked in the deformability measurement with the on-chip manipulation system. To overcome the limitation and obtain the full information of elastic and viscous coefficients, many efforts have been recently made [60,61,62,63,64]. The basic strategies can be classified into two concepts: (1) integration of the fluctuation analysis or (2) quantification of hydrodynamic force. (1) Integration of the fluctuation analysis was achieved by utilizing the on-chip cell manipulation, which enables to keep the cell position constant inside a microchannel. Ito and the coauthors compared the surface tension, bending stiffness, and viscosity with the parameter ratios obtained in the shape recovery, and found negative/positive correlations between them, indicating how the unit of force should be related with the assumed springs and dampers [60]. (2) The quantification of a hydrodynamic force was challenged with a support of a computational simulation. Kirimoto and the coauthors experimentally observed the flow profile surrounding a flowing RBC, and estimated the viscous stress on the surface of a RBC. Using the on-chip manipulation, they measured step response [61] and dynamic responses of the amplitude and phase to a sinusoidal input [62, 63], which provided the effective Young’s modulus and viscosity consistent with the other conventional measurements [7, 22].
In the end of the section, we mention the on-chip manipulation system with other setups. Guo and the coauthors have reported an active pressure control system for microchannels, and developed microfluidic pipette aspiration techniques for measuring the single-cell deformability [65, 66]. In their system, the pressure attenuator composed of a parallel long fluidic circuit is implemented and controlled from a program code. Their design demonstrated the 10−2 reduction of the externally applied pressure, and succeeded in the precise cell positioning. Compared to this work, the remarkable feature of our on-chip cell manipulation system is the high-speed, realtime, and thus spatio-temporally precise feedback position control. The high-speed manipulation allows the evaluation of the step response and hydrodynamic shear stress strong enough to deform a cell. On the whole, we believe that the next-generation microfluidics will develop with these emerging techniques for precise control and measurement in a microchannel.
Specific features of cellular mechanics: loading effect
In the previous section, we introduced the on-chip manipulation system and the results of the deformability measurement. For deeper understanding of the mechanism of the nonlinear deformability that depends on the loading time and the metabolic energy (amount of ATP), we need to see the internal structure of the cell.
The microfluidic platforms are especially suitable for non-adherent cells since these cells are suspended in an aqueous solution and thus the mechanical properties under natural condition can be measured. The most typical examples of non-adherent cells are blood cells: RBCs, white blood cells (WBCs), and platelets. They occupy about 40% volume of the whole blood, and flowing inside blood vessels. Since the RBCs occupy about 96% volume among the blood cells, RBC mechanics and deformability have been regarded as the most important factor to characterize the rheology of the blood. Actually, the RBCs easily deform during the blood circulation, where they are exposed to wall shear stress and spatial confinement inside the blood vessels. Since the dimension of a RBC, 8 µm in diameter and 2 µm in thickness [34], is larger than the smallest blood vessels, they experience large deformation during the microcirculation. Such deformability is the physiologically essential property of RBCs to realize the smooth microcirculation.
Compared to eukaryotic cells, the internal structure and functions of a RBC are much simpler; it has neither nucleus nor organelles, and the cytosol mainly consists of dense hemoglobin solution, sometimes regarded as just a bag of hemoglobin [39]. The simpler cytosol with no large structures is actually advantageous for the large deformation of a RBC. In addition to the cytoplasmic structure, the cytoskeleton is also different from that of typical eukaryotic cells in both the protein component and the higher-order network shape; it mainly consists of filaments formed by the tetramers of spectrin proteins, which are connected to the cell membrane via the short actin chain and various membrane proteins. The overall structure of the cytoskeletal filaments in a RBC is the hexagonal network pinned underneath the cell membrane [67, 68]. The cell membrane of a RBC is also an important structure to ensure the bending stiffness and keep almost constant surface area of the cell. It mainly consists of lipid bilayer membrane and embedded additional membrane proteins such as ion channels, ion pumps, molecular sensors, and linkers to other proteins. The typical value of bending stiffness is small as 10−19 N m [13], which is similar to that of pure lipid bilayer membrane, and thus the large folding deformation is allowed. On the other hand, the typical value of the area expansion modulus is much larger as 10−1 N/m [69], which is 6 orders of magnitude larger than the bending stiffness in the same length-scale deformation. Thus, the RBC membrane is easily bent by keeping the surface area when it is exposed to the mechanical stresses. For the viscosity of the deformation, the membrane viscosity with a typical value of 10−6 N s/m is known as the dominant factor [70].
While the above structures represent the static mechanical properties of a RBC, the RBC also exhibit ATP-dependent mechanical responses, which is the characteristic feature of living materials. The metabolic functions in a RBC are known to be attributed to the phosphorylation of various proteins such as protein 4.1 [71], band-3 [72, 73], ankyrin [74], actin [75,76,77], myosin [78], and spectrin [79]. Although the whole cell mechanics is complicated and the exact details for the ATP-dependent deformability is still unclear [57], future experiments with inhibitions of specific protein activities or knock out samples will contribute to deeper understanding and applications to novel mechanisms investigated in robotics and mechatronics.
Medical applications
Finally, in this section, we remark about the applications of the cellular deformability measurements to medical and diagnostic fields. Up to here we introduced various mechanical properties ranging from the aspect ratio to the viscoelastic coefficients such as bending stiffness, area expansion modulus, shear modulus, membrane viscosity, cytosolic viscosity, and Young’s modulus. These values and their specific dependences on deformation amplitude, period, frequency as well as ATP amount, can be used as biomarkers for the evaluation of the pathological conditions of the cell. For these purposes, a number of studies have reported that the mechanical properties of a single cell are altered, and often loses the flexible deformability, under diseased states. In the following, we briefly introduce typical blood diseases related to the modifications of RBC deformability and typical examples of microfluidic investigations for the diseases.
Sickle cell disease is an example of hereditary disorders of RBCs, in which genetically mutated hemoglobin (sickle hemoglobin; HbS) forms abnormally polymerized aggregations, and causes disorders in O2 transport, leading to anemia. Such RBCs have a sickle shape and exhibit more rigid and viscous mechanical property [80]. Thus, in addition to the reduced O2 transport by hemoglobin mutation, they also tend to disrupt the smooth microcirculations of the blood itself. Microfluidic channels have been used for evaluation of the sickle cell disease. For example, a microchannel that mimics a physiological vascular network has been used to evaluate the experimental parameters such as driving pressure and oxygen concentration for vaso-occlusive events [81].
Infection to malaria species such as Plasmodium vivax and Plasmodium falciparum is also a widely known disease for RBCs. As the infected malaria parasite in a host RBC matures in a 48-h cycle from ring forms to trophozoites and schizonts, the healthy biconcave cell shape is modified and the flexibility is decreased [82, 83]. These changes also depend on the four species of malaria [84]. Using microfluidics, Handayani and the coauthors studied the passage ability of Plasmodium vivax-infected RBCs through a microfluidic channel with 2 µm width, and found that the successful transit rate decreased according to the maturation of malaria-infection states [83]. For Plasmodium falciparum, Bow and the coauthors demonstrated the high-throughput screening and diagnosis of a small population of ring-stage infected RBCs by measuring the passing velocity of blood cells through a microfluidic constriction [85].
Sepsis is known as one of blood-related diseases that cause systematic inflammatory responses [86]. The septic shock is induced by the lipopolysaccharides (LPSs) released from the outer membrane of Gram-negative bacteria [87]. Many reports have suggested that LPSs cause the stiffening of RBCs, and disturb the smooth microcirculation [88,89,90]. Ito and the coauthors performed the measurements of the alteration of mechanical properties using microfluidic platforms, where they found the shear modulus of RBCs exposed to LPSs became larger, and RBCs exhibited shorter recovery time compared to that in healthy RBCs [57].
The patients need correct, accurate and fast decision-making and treatments as much as possible. When microfluidic devices are used for medical and diagnostic purposes, both the information content and throughput of the assays are critically important. In this sense, the developments of next-generation microfluidic techniques that achieve both better readouts and higher throughput are expected in this fields. In addition, more improvements in the user interface of microfluidic devices and software are also important requirements for the usage in the clinical situations by clinical doctors, not only by engineers in laboratories. In this paradigm, automation of both the hardware and software is another important topic to be addressed, and has been intensively investigated [91,92,93,94,95]. For the on-chip cell manipulation, we are also developing the automation of the gain-tuning toward clinical usages [96]. Although these requirements seem to be mature in macroscopic robotics such as in robot-assisted treatments by the da Vinci surgical robotic system (Intuitive Inc.) and robot-assisted biological assays by Mahoro (Robotic Biology Institute Inc.), microfluidic tools for biological materials are still in an emerging stage.
Conclusions
In this review, we summarize the experimental techniques for the measurements of cellular deformability, especially focusing on microfluidic techniques of RBC deformability evaluations. While passive microfluidics that drives the channel flow at a constant flow rate has been widely used for the deformability test in various research fields, active microfluidics that controls the flow and the suspended object in a realtime way has been recently developed, by combining robotics and mechatronics with the microscopic biological materials.
The desired control of the positioning of a target object is a universal requirement for various processes to treat a single cell. In this context, the research scope of the on-chip cell manipulation techniques in actively controlled microfluidics is still expanding. Not only to improve the performance but also to overcome the existing qualitative limitations, the technological aspect is being developed by incorporating modern technologies such as artificial intelligence (AI) and automation. If such programmable or automated on-chip manipulation is integrated, for example, into the organ-on-chip systems, it might realize the “on-chip printing” of organ structures by distinguishing the deformability of individual stem cells, which has a great impact on the fields of biotechnology and medicine. In the interdisciplinary research fields ranging from engineering, science to medicine, we believe that robotics and mechatronics play key roles to develop novel measuring tools and overcome the conventional limitations. In this sense, the microfluidic measurements of cellular deformability are the frontier where biological materials and robotics/mechatronics meet and integrate each other.
Availability of data and materials
Not applicable.
Abbreviations
- MEMS:
-
micro electro mechanical systems
- RBC:
-
red blood cell
- WBC:
-
white blood cell
- HbS:
-
sickle hemoglobin
- CTC:
-
circulating tumor cell
- LPS:
-
lipopolysaccharide
References
Alberts B, Johnson A, Lewis J, Morgan D, Raff M, Roberts K, Walter P (eds) (2014) Molecular biology of the cell, 6th edn. Garland Science, New York
Kollmannsberger P, Fabry B (2011) Linear and nonlinear rheology of living cells. Ann Rev Mater Res 41:75–97
Cross SE, Jin Y-S, Rao J, Gimzewski JK (2007) Nanomechanical analysis of cells from cancer patients. Nat Nanotechnol 2:780–783
Guillaume-Gentil O, Potthoff E, Ossola D, Franz CM, Zambelli T, Vorholt JA (2014) Force controlled manipulation of single cells: from AFM to FluidFM. Trends Biotechnol 32:381–388
Luo Q, Kuang D, Zhang B, Song G (2016) Cell stiffness determined by atomic force microscopy and its correlation with cell motility. Biochim Biophys Acta 1860:1953–1960
Dumitru AC, Poncin MA, Conrard L, Dufrêne F, Tyteca D, Alsteens D (2018) Nanoscale membrane architecture of healthy and pathological red blood cells. Nanoscale Horiz 3:293–304
Dao M, Lim CT, Suresh S (2003) Mechanics of the human red blood cell deformed by optical tweezers. J Mech Phys Soilds 51:2259–2280
Mills JP, Qie L, Dao M, Lim CT, Suresh S (2004) Nonlinear elastic and viscoelastic deformation of the human red blood cell with optical tweezers. Mech Chem Biosyst 1:169–180
Bausch AR, Ziemann F, Boulbitch AA, Jacobson K, Sackmann E (1998) Local measurements of viscoelastic parameters of adherent cell surfaces by magnetic bead microrheometry. Biophys J 75:2038–2049
Fabry B, Maksym GN, Butler JP, Glogauer M, Navajas D, Fredberg JJ (2001) Scaling the microrheology of living cells. Phys Rev Lett 87:148102
Kollmannsberger P, Fabry B (2008) High-force magnetic tweezers with force feedback for biological applications. Rev Sci Instrum 78:114301
Brochard F, Lennon J (1975) Frequency spectrum of the flicker phenomenon in erythrocytes. J Phys France 36:1035–1047
Yoon Y, Hong H, Brown A, Kim DC, Kang DJ, Lew VL, Cicuta P (2009) Biophys J 97:1606–1615
Betz T, Sykes C (2012) Time resolved fluctuation spectroscopy. Soft Matter 8:5317–5326
Caspi A, Granek R, Elbaum M (2000) Enhanced diffusion in active intracellular transport. Phys Rev Lett 85:5655–5658
Yamada S, Wirtz D, Kuo SC (2000) Mechanics of living cells measured by laser tracking microrheology. Biophys J 78:1736–1747
Wirtz D (2009) Particle tracking microrheology of living cells: principles and applications. Annu Rev Biophys 38:301–326
Nishizawa K, Fujiwara K, Ikenaga M, Nakajo N, Yanagisawa M, Mizuno D (2017) Universal glass-forming behavior of in vitro and living cytoplasm. Sci Rep 7:15143
Guck J, Chilvers ER (2013) Mechanics meets medicine. Sci Transl Med 5:212fs41
Wu P-H, Aroush DR-B, Asnacios A, Chen W-C, Dokukin ME, Doss BL, Durand-Smet P, Ekpenyong A, Guck J, Guz NV, Janmey PA, Lee JSH, Moore NM, Ott A, Poh Y-C, Ros R, Sander M, Sokolov I, Staunton JR, Wang N, Whyte G, Wirtz D (2018) A comparison of methods to assess cell mechanical properties. Nat Methods 15:491–498
Mason TG (2000) Estimating the viscoelastic moduli of complex fluids using the generalized Stokes-Einstein equation. Rheol Acta 39:371–378
Hochmuth RM, Worthy PR, Evans EA (1979) Red cell extensional recovery and the determination of membrane viscosity. Biophys J 26:101–114
Evans EA, La Celle PL (1975) Intrinsic material properties of the erythrocyte membrane indicated by mechanical analysis of deformation. Blood 45:29–43
Discher D, Mohandas N (1996) Kinematics of red cell aspiration by fluorescence-imaged microdeformation. Biophys J 71:1680–1694
Lu H, Yang Y, Lin X, Shi P, Shen Y (2019) Low-invasive cell injection based on rotational microrobot. Adv Biosyst 3:1800274
Shang W, Lu H, Wan W, Fukuda T, Shen Y (2016) Vision-based nano robotic system for high-throughput non-embedded cell cutting. Sci Rep 6:22534
Tanikawa T, Arai T (1999) Development of a micro-manipulation system having a two-fingered micro-hand. IEEE Trans Robot Autom 15:152–162
Suzuki Y (1996) Flexible microgripper and its application to micromeasurement of mechanical and thermal properties. In: Proceedings of ninth international workshop on micro electromechanical systems, San Diego, USA
Desai JP, Pillarisetti A, Brooks AD (2007) Engineering approaches to biomanipulation. Annu Rev Biomed Eng 9:35–53
Veschgini M, Gebert F, Khangai N, Ito H, Suzuki R, Holstein TW, Mae Y, Arai T, Tanaka M (2016) Tracking mechanical and morphological dynamics of regenerating Hydra tissue fragments using a two fingered micro-robotic hand. Appl Phys Lett 108:103702
Shen Y, Fukuda T (2014) State of the art: micro-nanorobotic manipulation in single cell analysis. Robot Biomimetics 1:21
Shojaei-Baghini E, Zheng Y, Sun Y (2013) Automated micropipette aspiration of single cells. Ann Biomed Eng 41:1208–1216
Skalak R, Branemark P (1969) Deformation of red blood cells in capillaries. Science 164:717–719
Secomb T (2017) Blood flow in the microcirculation. Ann Rev Fluid Mech 49:443–461
Chen X, Cui DF, Liu CC, Li H (2008) Microfluidic chip for blood cell separation and collection based on crossflow filtration. Sens Actuators B 130:216–221
Wang G, Crawford K, Turbyfield C, Lam W, Alexeev A, Sulchek T (2015) Microfluidic cellular enrichment and separation through differences in viscoelastic deformation. Lab Chip 15:532–540
Sollier E, Go DE, Che J, Gossett DR, O’Byrne S, Weaver WM, Kummer N, Rettig M, Goldman J, Nickols N, McCloskey S, Kulkarni RP, Carlo DD (2014) Size-selective collection of circulating tumor cells using vortex technology. Lab Chip 14:63–77
Guillou L, Dahl JB, Lin J-MG, Barakat AI, Husson J, Muller SJ, Kumar S (2016) Measuring cell viscoelastic properties using a microfluidic extensional flow device. Biophys J 111:2039–2050
Brody JP, Han Y, Austin RH, Bitensky M (1995) Deformation and flow of red blood cells in a synthetic lattice: evidence for an active cytoskeleton. Biophys J 68:2224–2232
Abkarian M, Faivre M, Horton R, Smistrup K, Best-Popescu CA, Stone HA (2008) Cellular-scale hydrodynamics. Biomed Mater 3:034011
Tomaiuolo G, Barra M, Preziosi V, Cassinese A, Rotoli B, Guido S (2011) Microfluidics analysis of red blood cell membrane viscoelasticity. Lab Chip 11:449–454
Quinn DJ, Pivkin I, Wong SY, Chiam K-H, Dao M, Karniadakis GE, Suresh S (2011) Combined simulation and experimental study of large deformation of red blood cells in microfluidic systems. Ann Biomed Eng 39:1041–1050
Zheng Y, Shojaei-Baghini E, Azad A, Wang C, Sun Y (2012) High-throughput biophysical measurement of human red blood cells. Lab Chip 12:2560–2567
Prado G, Farutin A, Misbah C, Bureau L (2015) Viscoelastic transient of confined red blood cells. Biophys J 108:2126–2136
Tsai C-HD, Tanaka J, Kaneko M, Horade M, Ito H, Taniguchi T, Ohtani T, Sakata Y (2016) An on-chip RBC deformability checker significantly improves velocity-deformation correlation. Micromachines 7:176
Wan J, Ristenpart WD, Stone HA (2008) Dynamics of shear-induced ATP release from red blood cells. Proc Natl Acad Sci USA 105:16432–16437
Gossett DR, Tse HTK, Lee SA, Ying Y, Lindgren AG, Yang OO, Rao J, Clark AT, Carlo DD (2012) Hydrodynamic stretching of single cells for large population mechanical phenotyping. Proc Natl Acad Sci USA 109:7630–7635
Otto O, Rosendahl P, Mietke A, Golfier S, Herold C, Klaue D, Girardo S, Pagliara S, Ekpenyong A, Jacobi A, Wobus M, Töpfner N, Keyser UF, Mansfeld J, Fischer-Friedrich E, Guck J (2015) Real-time deformability cytometry: on-the-fly cell mechanical phenotyping. Nat Methods 12:199–202
Mietke A, Otto O, Girardo S, Rosendahl P, Taubenberger A, Golfier S, Ulbricht E, Aland S, Guck J, Fischer-Friedrich E (2015) Extracting cell stiffness from real-time deformability cytometry: theory and experiment. Biophys J 109:2023–2036
Mancuso JE, Ristenpart WD (2017) Stretching of red blood cells at high strain rates. Phys Rev Fluid 2:101101
Xu Z, Zheng Y, Wang X, Shehata N, Wang C, Sun Y (2018) Stiffness increase of red blood cells during storage. Microsyst Nanoeng 4:17103
Braunmüller S, Schmid L, Sackmann E, Franke T (2012) Hydrodynamic deformation reveals two coupled modes/time scales of red blood cell relaxation. Soft Matter 8:11240–11248
Sakuma S, Kuroda K, Arai F, Taniguchi T, Ohtani T, Sakata Y, Kaneko M (2014) High resolution cell positioning based on a flow reduction mechanism for enhancing deformability mapping. Micromachines 5:1188–1201
Mizoue K, Teramura K, Tsai C-HD, Kaneko M (2017) Transfer function of macro-micro manipulation on a PDMS microfluidic chip. Micromachines 8:80
Sakuma S, Kuroda K, Tsai C-HD, Fukui W, Arai F, Kaneko M (2014) Red blood cell fatigue evaluation based on the close-encountering point between extensibility and recoverability. Lab Chip 14:1135–1141
Murakami R, Tsai C-HD, Ito H, Tanaka M, Sakuma S, Arai F, Kaneko M (2016) Catch, load and launch toward on-chip active cell evaluation. In: Proceedings of 2016 IEEE international conference on robotics and automation (ICRA2016), Stockholm
Ito H, Murakami R, Sakuma S, Tsai C-HD, Gutsmann T, Brandenburg K, Pöschl JMB, Arai F, Kaneko M, Kaneko M (2017) Mechanical diagnosis of human erythrocytes by ultra-high speed manipulation unraveled critical time window for global cytoskeletal remodeling. Sci Rep 7:43134
Horade M, Tsai C-HD, Ito H, Kaneko M (2017) Red blood cell responses during a long-standing load in a microfluidic constriction micromachines. Micromachines 8:100
Ito H, Fujimoto K, Kaneko M (2019) On-chip deformability measurement of eukaryotic cells: comparison to anucleate cells. In: Proceedings of the 23rd international conference on miniaturized systems for chemistry and life sciences (MicroTAS2019), Basel
Ito H, Tsai C-HD, Kaneko M (2018) Integration of fluctuation spectroscopy into a microfluidic platform for novel cellular viscoelastic measurement. In: Proceedings of the 31st IEEE international conference on micro electro mechanical systems (MEMS2018), Belfast
Kirimoto A, Ito H, Tsai C-HD, Kaneko M (2018) Measurement of both viscous and elastic constants of a red blood cell in a microchannel. In: Proceedings of The 31st IEEE international conference on micro electro mechanical systems (MEMS2018), Belfast
Ito H, Takeishi N, Kirimoto A, Chimura M, Ohtani T, Sakata Y, Horade M, Takayama T, Wada S, Kaneko M (2019) How to measure cellular shear modulus inside a chip: Detailed correspondence to the fluid-structure coupling analysis. In: Proceedings of the 32nd IEEE international conference on micro electro mechanical systems (MEMS2019), Seoul
Kirimoto A, Ito H, Horade M, Takayama T, Chimura M, Ohtani T, Sakata Y, Kaneko M (2019) On-chip dynamic mechanical measurement. In: Proceedings of the 32nd IEEE international conference on micro electro mechanical systems (MEMS2019), Seoul
Takeishi N, Ito H, Kaneko M, Wada S (2019) Deformation of a red blood cell in a narrow rectangular microchannel. Micromachines 10:199
Guo Q, Park S, Ma H (2012) Microfluidic micropipette aspiration for measuring the deformability of single cells. Lab Chip 12:2687–2695
Guo Q, Duffy SP, Matthews K, Santoso AT, Scott MD, Ma H (2014) Microfluidic analysis of red blood cell deformability. J Biomech 47:1767–1776
Byers TJ, Branton D (1985) Visualization of the protein associations in the erythrocyte membrane skeleton. Proc Natl Acad Sci USA 82:6153–6157
Liu S-C, Derick LH, Palek J (1987) Visualization of the hexagonal lattice in the erythrocyte membrane skeleton. J Cell Biol 104:527–536
Lenormand G, Hénon S, Richert A, Siméon J, Gallet F (2001) Direct measurement of the area expansion and shear moduli of the human red blood cell membrane skeleton. Biophys J 81:43–56
Evans EA, Hochmuth RM (1976) Membrane viscoelasticity. Biophys J 16:1–11
Manno S, Takakuwa Y, Mohandas N (2005) Modulation of erythrocyte membrane mechanical function by protein 4.1 phosphorylation. J Biol Chem 280:7581–7587
Harrison ML, Rathinavelu P, Arese P, Geahlen RL, Low PS (1991) Role of band 3 tyrosine phosphorylation in the regulation of erythrocyte glycolysis. J Biol Chem 266:4106–4111
Ferru E, Giger K, Pantaleo A, Campanella E, Grey J, Ritchie K, Vono R, Turrini F, Low PS (2011) Regulation of membrane-cytoskeletal interactions by tyrosine phosphorylation of erythrocyte band 3. Blood 117:5998–6006
Lu P-W, Soong C-J, Tao M (1985) Phosphorylation of ankyrin decreases its affinity for spectrin tetramer. J Biol Chem 260:14958–14964
Tuvia S, Levin S, Bitler A, Korenstein R (1998) Mechanical fluctuations of the membrane-skeleton are dependent on F-actin ATPase in human erythrocytes. J Cell Biol 141:1551–1561
Gokhin DS, Nowak RB, Khoory JA, de la Piedra A, Ghiran IC, Fowler VM (2015) Dynamic actin filaments control the mechanical behavior of the human red blood cell membrane. Mol Biol Cell 26:1699–1710
Gokhin DS, Fowler VM (2016) Feisty filaments: actin dynamics in the red blood cell membrane skeleton. Curr Opin Hematol 23:206–214
Smith Q, Rochman N, Carmo AM, Vig D, Chan XY, Sun S, Gerecht S (2018) Cytoskeletal tension regulates mesodermal spatial organization and subsequent vascular fate. Proc Natl Acad Sci USA 115:8167–8172
Manno S, Takakuwa Y, Nagao K, Mohandas N (1995) Modulation of erythrocyte membrane mechanical function by β-spectrin phosphorylation and dephosphrylation. J Biol Chem 270:5659–5665
Evans E, Mohandas N, Leung A (1987) Static and dynamic rigidities of normal and sickle erythrocytes. J Clin Invest 73:477–488
Higgins JM, Eddington DT, Bhatia SN, Mahadevan L (2007) Sickle cell vasoocclusion and rescue in a microfluidic device. Proc Natl Acad Sci USA 104:20496–20500
Suresh S, Spatz J, Mills JP, Micoulet A, Dao M, Lim CT, Beil M, Seufferlein T (2005) Connections between single-cell biomechanics and human disease states: gastrointestinal cancer and malaria. Acta Biomater 1:15–30
Handayani S, Chiu DT, Tjitra E, Kuo JS, Lampah D, Kenangalem E, Renia L, Snounou G, Price RN, Anstey M, Russell B (2009) High deformability of Plasmodium vivax-infected red blood cells under microfluidic conditions. J Infect Dis 199:445–450
Swanarusk R, Cooke BM, Dondorp AM, Silamut K, Sattabongkot J, White NJ, Udomsangpetch R (2004) The deformability of red blood cells parasitized by Plasmodium falciparum and P. vivax. J Infect Dis 189:190–194
Bow H, Pivkin IV, Diez-Silva M, Goldfless SJ, Dao M, Niles JC, Suresh S, Han J (2011) A microfabricated deformability-based flow cytometer with application to malaria. Lab Chip 11:1065–1073
Hotchkiss RS, Karl IE (2003) The pathophysiology and treatment of sepsis. N Engl J Med 348:138–150
Lüderitz O, Freudenberg MA, Galanos C, Lehmann V, Rietschel ET, Shaw DH, Razin CS, Rottem S (1982) Current topics in membranes and transport. Academic Press, New York
Pöschl JMB, Linderkamp O (1992) Effect of lipid A on the deformability, membrane rigidity, and geometry of human adult red blood cells. Eur J Clin Invest 22:625–629
Piagnerelli M, Boudjeltia KZ, Vanhaeverbeek M, Vincent J-L (2003) Red blood cell rheology in sepsis. Intensive Care Med 29:1052–1061
Condon MR, Kim JE, Deitch A, Machiedo GW, Spolarics Z (2003) Appearance of an erythrocyte population with decreased deformability and hemoglobin content following sepsis. Am J Physiol Heart Circ Physiol 284:H2177–H2184
Ito H, Kuss N, Rapp BE, Ichikawa M, Gutsmann T, Brandenburg K, Pöschl JMB, Tanaka M (2015) Quantification of the influence of endotoxins on the mechanics of adult and neonatal red blood cells. J Phys Chem B 119:7837–7845
Du G, Fang Q, den Toonder JMJ (2016) Microfluidics for cell-based high throughput screening platforms–A review. Anal Chim Acta 903:36–50
Lin J, Kim D, Tse HT, Tseng P, Peng L, Dhar M, Karumbayaram S, Di Carlo Dino (2017) High-throughput physical phenotyping of cell differentiation. Microsyst Nanoeng 3:17013
Rosendahl P, Plak K, Jacobi A, Kraeter M, Toepfner N, Otto O, Herold C, Winzi M, Herbig M, Ge Y, Girardo S, Wagner K, Baum B, Guck J (2018) Real-time fluorescence and deformability cytometry. Nat Methods 15:355–358
Nitta N et al (2018) Intelligent image-activated cell sorting. Cell 175:1–11
Ito H, Komiya T, Horade M, Takayama T, Kaneko M (2018) Automatically optimized on-chip feedback manipulation toward clinical use. In: Proceedings of the 22nd international conference on miniaturized systems for chemistry and life sciences (MicroTAS2018), Kaohsiung
Acknowledgements
This work was supported by JSPS KAKENHI Grant Numbers JP19H00749, JP19K14675, and by Sumitomo Foundation (No. 181161).
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
HI and MK contributed to the conception of the review, and writing the final manuscript. Both authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ito, H., Kaneko, M. On-chip cell manipulation and applications to deformability measurements. Robomech J 7, 3 (2020). https://doi.org/10.1186/s40648-020-0154-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40648-020-0154-x