Abstract
Coupled shear walls are efficient in resisting lateral forces induced by winds and earthquakes. However, it is difficult to construct coupled shear walls particularly because current design codes require complex reinforcing details within coupling beams. The objective of this study was to develop simple reinforcement details for diagonally reinforced coupling beams; reducing transverse steel by use of high-performance fiber-reinforced cementitious composites (HPFRCCs) and bundling diagonal bars are explored. Four coupling beam specimens with length-to-depth aspect ratios of 2.0 or 3.5 were fabricated and tested under cyclic lateral displacements. The test results revealed that HPFRCC coupling beams with bundled diagonal bars and widely spaced transverse reinforcement (one-half the amount of reinforcement required by current seismic codes) exhibited excellent seismic performance compared with ordinary concrete coupling beams having code-required distributed diagonal reinforcement and transverse reinforcement.
Similar content being viewed by others
1 Introduction
Coupled wall systems consisting of separate shear walls linked together by coupling beams at floor levels are effective in resisting wind- and earthquake-induced forces in high-rise buildings (Paulay and Priestley 1992). When subjected to design-level earthquakes, coupling beams designed according to current design codes (NZS 1982; CEN 2004; ACI 2014) are expected to suffer substantial inelastic deformations and to dissipate significant amount of energy (MacGregor and Wight 2009); they play a key role in the seismic performance of the entire coupled wall system. Therefore, coupling beams should be equipped with adequate reinforcement details that perform well during seismic events, providing adequate ductility and energy dissipation, as well as strength and stiffness (Paulay and Priestley 1992; MacGregor and Wight 2009).
Coupling beams reinforced by means of a conventional detail, with longitudinal bars parallel to the span of the beam, may experience sliding shear failure near the beam ends at which flexural cracks caused by reversed cyclic loading come across one another (Paulay 1971). Transverse reinforcement is not capable of preventing sliding shear failure when flexural cracks propagate across the entire depth of the beam between stirrups (Paulay and Priestley 1992). Many studies have been conducted with the aim of resolving this problem. Historically, Paulay and Binney (1974) first developed diagonal reinforcement for coupling beams. Diagonally reinforced coupling beams strongly resist sliding and have ductility, energy dissipation, and stiffness retention capacities superior to those conventionally reinforced coupling beams (Paulay and Binney 1974; Barney et al. 1980; Tassios et al. 1996; Galano and Vignoli 2000; Harries et al. 2005; Fortney et al. 2008; Wallace 2012; Naish et al. 2013).
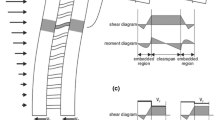
Based on the previous studies mentioned above, section 18.10.7 in ACI 318-14 (ACI 2014) specifies two confinement options for coupling beams with diagonal reinforcement (Fig. 1). In the first option, each group of diagonal reinforcement comprises at least four longitudinal bars enclosed by densely spaced transverse reinforcement (Fig. 1a). This confinement method entails a very intricate arrangement of reinforcement, especially at the mid-span of the beam where opposite diagonal reinforcement groups meet each other. According to Harries et al. (2005), the first confinement option is practically difficult to construct when the average shear stress in the beam is greater than \( 0.5\sqrt {f'_{c} } \) MPa, where f’ c is the concrete compressive strength in MPa. Due to such shortcomings, a second confinement option is allowed by section 18.10.7.4(d) in ACI 318-14, in which transverse reinforcement required for beams and columns of special moment frames is provided for the entire cross section of the beam, as a replacement for transverse reinforcement directly enclosing diagonal bars (Fig. 1b). However, reinforcement congestion remains a problem when he second option is used, especially near the midspan of the beam, where horizontal crossties conflict with diagonal bars.
Diagonally reinforced coupling beams [a, b options specified in ACI 318-14 (ACI 2014), and c option with bundled diagonal reinforcement].
In efforts to resolve the difficulty of fabricating diagonal reinforcement in coupling beams, various reinforcing details have been investigated and proposed to date (Tassios et al. 1996; Galano and Vignoli 2000; Han et al. 2015). Han et al. (2015) recently tested the efficiency of bundled diagonal reinforcement in reinforced concrete (RC) coupling beams. Bundled diagonal reinforcement allows more internal space, enhancing workability and allowing simple construction, compared with code-specified diagonal reinforcement in which spacers are needed to maintain the gaps between separate diagonal bars. Bundling also increases the angle of diagonal reinforcement measured from the longitudinal axis of the beam, thereby increasing both flexural and shear strength. Han et al. (2015) reported that coupling beams having bundled diagonal reinforcement achieved greater strength and energy dissipation than, and a similar displacement ductility to, those with code-specified diagonal reinforcement.
During the last decade, research groups (Canbolat et al. 2005; Parra-Montesinos et al. 2005; Parra-Montesinos 2005; Naaman et al. 2007; Lequesne et al. 2010; Olsen and Billington 2011; Shin et al. 2014) have investigated the effectiveness of high performance fiber-reinforced cement composites (HPFRCCs) with respect to earthquake resistance of structures. HPFRCCs are characterized by strain-hardening behavior in uniaxial tension by developing numerous micro-cracks with the assistance of a small portion of engineered fibers (Li 2003; Naaman 2003; Kim et al. 2007, 2009; Li 2012). HPFRCCs generally show much higher ductility than normal concrete, under both tension and compression. Thus, the use of HPFRCC may relieve the confinement requirements of members with highly congested reinforcement (Parra-Montesinos 2005). When subjected to seismic forces, HPFRCCs are deemed to improve energy dissipation by means of fiber bridging over micro-cracks and excellent bonding between the reinforcing steel and cement within the composite (Li 2003).
Given the aforementioned concerns, the aim of the present work was to develop simple reinforcement details for diagonally reinforced coupling beams. For developing a simple reinforcement details for coupling beams and improving their seismic behavior, several studies have been also carried out using fiber reinforced coupling beams (Canbolat et al. 2005; Lequesne et al. 2010). This study also focused on application of HPFRCC to diagonally reinforced coupling beams. In particular, the effect of HPFRCCs in coupling beams with bundled diagonal reinforcement is investigated for the purpose of reducing the amount of transverse reinforcement required. In addition, to simplify construction as much as possible, the feasibility of precast coupling beam construction was explored. Four approximately half scale coupling beam specimens with the length-to-depth aspect ratios of 2.0 or 3.5 were fabricated and tested under cyclic lateral displacements.
2 Experimental Program
Four coupling beam specimens were constructed and tested in the present study. The primary goal of the tests was to investigate the cyclic behavior of HPFRCC coupling beams having bundled diagonal reinforcement and widely spaced transverse reinforcement.
2.1 Specimen Details
Figure 2 illustrates the dimensions and reinforcing details of the specimens. All specimens were reinforced with bundled diagonal reinforcement and also used the second confinement option illustrated in Fig. 1c. The main test variables were the use of conventional RC or the use of HPFRCC in combination with reduced transverse reinforcement, and the use of two different aspect ratios (l n /l n h.h) where l n and h are the length and overall depth of the beam. Table 1 summarizes the test variables and specimen dimensions. The HPFRCC used in this study contained polyvinyl alcohol (PVA) fibers. The PVA fiber content in the HPFRCC was 2% by volume. The reduced amount of transverse reinforcement was about one half that required by section 18.10.7.4(d) in ACI 318-14. The aspect ratio (l n /h) of coupling beams was selected to be either 2.0 or 3.5 to respectively represent typical deep or slender coupling beams in high-rise residential buildings.
The beam length was 1050 mm in all specimens, and the beam depth was 525 or 300 mm. The total area of diagonal bars was determined so that the average shear stress in the coupling beam would be limited to approximately \( 0.5\sqrt {f'_{c} } \) MPa. The spacing of transverse reinforcement was 120 and 110 mm in the specimens with l n /h of 2.0 and 3.5 respectively, not exceeding six times the diagonal bar diameter as required in ACI 318-14 section 18.10.7.4(d). The inclination angles of bundled diagonal reinforcement in the specimens with the aspect ratios of 2.0 and 3.5 were about 22.1° and 10.7°, respectively. ACI 318-14 (ACI 2014) specifies that horizontal reinforcement in diagonally reinforced coupling beams (Fig. 1), mainly used to provide anchorage for horizontal crossties, shall not develop the yield strength at walls. In this study, the embedment length of horizontal reinforcement into the top and bottom stubs was 50 mm in all specimens. For producing the sufficient anchorage of bundled diagonal bars, they were sufficiently extended to the top and bottom concrete stubs. The coupling beams with large extending bars may not be effective for construction. However, the focus of this study was to propose simple details for HPFRCC diagonally reinforced coupling beams by using bundled diagonal reinforcement and reducing transverse reinforcement. No simple detail for extended bundled bars was proposed in this study.
Figure 3 shows reinforcement cages assembled inside the coupling beam formworks before concrete placement. For comparison, the figure shows both Specimens RC-ACI-2.0 and RC-ACI-3.5 (Han et al. 2015) having distributed diagonal reinforcement designed according to section 18.10.7.4 in ACI 318-14.
Specimens RC-2.0 and RC-3.5 were RC coupling beams having the same reinforcement details as RC-ACI-2.0 and RC-ACI-3.5 respectively, except that they had bundled diagonal reinforcement. Specimens HC-2.0 and HC-3.5 represent HPFRCC coupling beams having bundled diagonal reinforcement and one half the code-required amount of transverse reinforcement. It is clearly demonstrated that both bundled diagonal reinforcement and widely spaced transverse reinforcement would make coupling beam construction easier.
It is difficult to arrange reinforcement for diagonal reinforced coupling beams in construction sites due to the complexity of their reinforcement and to cast concrete due to the reinforcement congestion in the coupling beam. Precast concrete (HPFRCC) coupling beams could alleviate the problem associated with constructing in situ coupling beams. To study the feasibility of precast construction of coupling beams, the beam portion was constructed first, and the stubs at the ends of the beam representing in situ shear walls were fabricated in the next step. It is noted that precast concrete coupling beams with large extended diagonal bundled bars may not be efficient for installing the beam in the construction site. However, this study did not attempt to investigate the anchorage method of bundled diagonal bars. This study focused on the use of HPFRCC, bundled diagonal reinforcement that increases inner space of the beam, and widely spaced transverse reinforcement in diagonally reinforced coupling beams.
To ensure adequate load transfer between the beam and stubs, 50 mm deep rectangular shear keys were crafted at the beam ends, and “U”-shaped reinforcement was also added at the interfaces between the beam and stubs (Fig. 2). To prevent the stubs from being damaged, they were built using concrete of a compressive strength of 60 MPa and sufficient reinforcement.
2.2 Loading Frame, Protocol, and Measurements
Figure 4 illustrates the test setup and loading protocol. The test setup was intended to represent the behavior of coupling beams subjected to lateral loading. The coupling beam was arranged vertically, and the steel frame rigidly connected to the top stub was loaded horizontally by a hydraulic actuator. Since coupling beam specimens were cast horizontally and then tested vertically, a prestressing force was applied in the specimen due to the weight of the specimen.
The weight of the top stub and beam, which was associated with the prestressing force, was 29.1 kN, which is only 0.01 A g f c ′ where A g is the gross sectional area of the coupling beam specimen and f c ′ is the measured compressive strength of the concrete or HPFRCC; thus, the prestressing effect due to the weight of the specimen was neglected in this study. The bottom stub was fixed to the strong floor with anchors. In order to enforce zero moment at the mid-span of the coupling beam, the axis of the actuator was arranged to pass through the mid-span. Also, two roller supports were installed near the ends of the steel frame to prevent the top stub from rotation but allow horizontal translation. Also, the supports were to restrain the elongation of the coupling beam. In a coupled wall system, coupling beams tends to elongate axially when lateral loading causes severe cracking in concrete and inelastic residual strains in the longitudinal bars. However, such elongation was restrained due to large in-plane stiffness and strength of adjoining shear walls, consequently imposing compression in the coupling beams (Barbachyn et al. 2012). Stoppers were installed at the ends of the bottom stub to prevent the specimen from sliding.
Quasi-static reversed cyclic loading was applied with controlled displacement as shown in Fig. 4b. The drift ratio is defined as the lateral displacement between the ends of the coupling beam divided by the beam length. For each drift ratio, two consecutive cycles of the same drift amplitude were applied to assess strength and stiffness degradations. The same loading protocol was used in all tests. Figure 5 displays the positions of linear variable differential transformers (LVDTs) installed on each specimen.
The lateral displacement of the coupling beam was measured by using two LVDTs (marked “Top” and “Bottom”) installed horizontally at the top stub; the two yielded similar displacements throughout testing. To monitor the possible sliding of the specimen, a horizontal LVDT (marked “Base”) was installed at the bottom stub. To assess flexural and shear deformations of the specimen, multiple vertical and diagonal LVDTs were installed at one side of the beam. Also, fixed-end rotations at the interfaces between the beams and stubs were monitored by using four vertical LVDTs (L5, L6, L7, and L8) located on the top and bottom faces of the beam. The actuator load was measured by a load cell, and the shear force in the coupling beam was assumed to be equal to the actuator load. Strain gauges were installed at selected locations on the diagonal, transverse, and horizontal reinforcement.
2.3 Material Tests
Compression and uniaxial (direct) tension tests were conducted to examine the properties of the normal concrete and HPFRCC used to construct the coupling beam specimens. Table 2 lists the proportions of the HPFRCC mixture. PVA fibers in the HPFRCC were 2.0% by volume. The water/PCM ratio was approximately 20%, where “PCM” stands for dry premixed cement mortar consisting of binder, fillers, and chemical admixtures. Table 3 summarizes the physical properties of the PVA fibers used in the HPFRCC. In the normal concrete, the maximum aggregate size was 25 mm, whereas the HPFRCC contained neither coarse nor fine aggregates.
For the compression tests, three cylindrical specimens having 100 mm in diameter and 200 mm in height were fabricated according to ASTM C39, and cured under the same condition as the coupling beam specimens. Three LVDTs in parallel were installed around the perimeter of the specimen in the loading direction to estimate the average compressive strain, with the gage length of approximately 90 mm.
Figure 6a shows the compressive stress–strain curves of the HPFRCC and normal concrete acquired after 28 days of curing. Both the HPFRCC and normal concrete showed slightly higher strengths than the design compressive strength of 40 MPa. The compressive stress–strain relationships indicated that the HPFRCC was much more ductile than the normal concrete; the strain measured at failure was approximately 67% greater for the HPRCC. On the other hand, the secant modulus of elasticity of the normal concrete was about 24% greater than that of the HPFRCC. The secant modulus was calculated according to ACI 318-14, which is the slope of a line passing through 45% of the maximum compressive strength in the stress–strain curve.
For direct tension tests, three dog-bone shaped specimens were fabricated, similar to those used by the University of Michigan research group (Parra-Montesinos 2005). Two LVDTs in parallel were mounted along the sides of the specimen to estimate the average tensile strain, with the gage length of approximately 180 mm.
Figure 6b shows the tensile stress–strain curve and cracking pattern of the HPFRCC used in this study. Under tension, the HPFRCC specimens showed ductile behavior by means of strain hardening, developing numerous well-distributed micro-cracks with the effect of fiber bridging (Li 2003; Naaman 2003; Kim et al. 2007, 2009; Li 2012). The maximum tensile strain exceeded 2.5%, and the tensile strength was approximately 4.3 MPa. Table 4 summarizes the compressive and tensile strengths of the HPFRCC and normal concrete measured at the curing age of 28 days.
The properties of reinforcing bars used in the coupling beam specimens were examined under uniaxial tension. Stress–strain curves of the reinforcing bars are shown in Fig. 7, and Table 5 summarizes the mechanical properties acquired from the tension tests.
3 Test Results and Observations
3.1 Cracking Damages and Failure Modes
Figure 8 shows cracking damages in the two specimens with the span-to-depth ratio of 2.0. In both specimens, a few horizontal (flexural) cracks formed at the beam ends in the very early stages; later, as the drift ration increased, inclined (diagonal tension) cracks spread over the entire span.
In specimen RC-2.0, made with normal concrete, bundled diagonal reinforcement and code-specified transverse reinforcement, inclined cracks began to develop at approximately 0.25% drift. By 2% drift, the width of inclined cracks increased to about 1.5 mm (Fig. 8a), and most diagonal bars underwent yielding near the beam-stub interfaces. At 5% drift, the inclined cracks widened to greater than 4.5 mm, and some spalling of concrete under compression occurred at the beam ends (Fig. 8b). Slight buckling in the diagonal bundled bars was observed. Eventually, at about 7% drift, RC-2.0 started to collapse owing to the rupture of some diagonal bars (Fig. 8c). It is noted that the crack patterns were somewhat asymmetric (Fig. 8) even though the rotation of the top stub (reaction block) was restrained by the supports of the guide columns. This may be resulted from an imperfect installation of the test setup.
Specimen HC-2.0, made with the HPFRCC, bundled diagonal reinforcement and one-half the code-specified transverse reinforcement, showed a pattern of flexural and diagonal tension cracks that was generally similar to that of Specimen RC-2.0. However, the inclined cracks in HC-2.0 were much narrower and more numerous than those in RC-2.0, as shown in Figs. 8d–f. Even at 5% drift, the inclined cracks remained less than 2 mm in width (Fig. 8e), less than half the cracks in RC-2.0 at the same drift. No buckling in the diagonal bars occurred in this specimen. Also, almost no spalling damage was observed in HC-2.0 by 7% drift (Fig. 8f), even though the specimen had completely failed, with the rupture of some diagonal bars.
Figure 9 shows cracking damage in the two specimens of a span-to-depth ratio of 3.5; these specimens underwent more flexural cracks near the beam ends than the specimens of a span-to-depth ratio of 2.0. The standard specimen RC-3.5 having code-specified transverse reinforcement suffered inclined cracking from about 0.75% drift. The inclined cracks widened to about 2 mm by 2% drift (Fig. 9a), with most diagonal bars yielding near the beam-stub interfaces. At 5% drift, the cracks widened to more than 5 mm, and some concrete spalled from the compression zones at the beam ends (Fig. 9b). Finally, RC-3.5 started to collapse from 10% drift, when several diagonal bars ruptured and severe concrete spalling occurred (Fig. 9c). In this specimen, buckling was clearly observed in the diagonal bundled bars.
The HPFRCC specimen HC-3.5, which was reinforced with bundled diagonal reinforcement and one-half the amount of code-specified transverse steel, showed early flexural cracks at 0.25% drift. By about 2% drift, numerous diagonal tension cracks spread over the entire span (Fig. 9d), and most diagonal bars underwent yielding. However, the cracks were less than 0.5 mm wide at 2% drift, only one-fourth the width of cracks in RC-3.5 at the same drift. As in the specimens of aspect ratio 2.0, the cracks in HC-3.5 were much narrower and fewer than those in RC-3.5, as shown in Figs. 9d–f. No buckling in diagonal bars was observed in HC-3.5. Also, HC-3.5 did not suffer any spalling damage, until it started to collapse with the rupture of some diagonal bars at 10% drift (Fig. 9f).
Considering that Specimens RC-2.0 and RC-3.5 maintained a steady strength up to about 6 and 10% drift respectively, the use of bundled diagonal reinforcement in combination with code-specified transverse reinforcement was considered to be an efficient solution for building coupling beams to resist cyclic lateral loading. Also, the test results suggested that the use of HPFRCC enabled a 50% reduction in the code-required amount of transverse reinforcement by providing effective confinement for bundled diagonal reinforcement, controlling the width of cracks and avoiding spalling damage.
3.2 Load–Displacement Responses
Figure 10 shows the cyclic shear-drift responses of the coupling beam specimens. The right side vertical axis of this figure indicates the normalized shear stress, namely, the ratio of shear force in the coupling beam, taken equal to the actuator load, to the product of the beam cross-sectional area (A cw ) and the square root of the concrete compressive strength (f ′ c ). Table 6 summarizes the yield load (V y ), yield drift ratio (θ y ), maximum load (V u ), maximum drift ratio (θ u ), and ductility ratio (μ) of each specimen. The yield and maximum drift ratios were determined according to the work of Pan and Moehle (1989). The yield drift ratio corresponds to the point of intersection between the secant line connecting the origin to the point of 2/3 of the maximum load and the horizontal line at the point of the maximum load. The maximum drift ratio was measured when the strength reduced to 80% of the maximum load. The ductility ratio is defined as the maximum drift divided by the yield drift.
Specimens RC-2.0 and RC-3.5 of normal concrete, composed of standard RC, having bundled diagonal reinforcement and code-specified transverse reinforcement exhibited stable load-drift behavior up to about 4 and 8% drift respectively, without considerable drop in strength. Between the two, the slender beam specimen showed much more ductility and had more full load-drift loops. The RC-2.0 specimen suffered significant and successive strength drops from the second cycle to 5% drift, when some diagonal and transverse reinforcement ruptured. In contrast, the higher-aspect-ratio specimen RC-3.5 sustained more than 80% of its maximum load up to the first positive loading cycle of 10% drift ratio. Thus, the ductility ratios of Specimens RC-2.0 and RC-3.5 for loading in the positive direction were approximately 3.0 and 5.7 in, respectively.
Specimens HC-2.0 and HC-3.5, composed of HPFRCC, having bundled diagonal reinforcement and one half the amount of code-specified transverse reinforcement, showed load-drift responses that were generally similar to those of the normal concrete specimens discussed above. HC-2.0 and HC-3.5 exhibited stable behavior up to 5 and 8% drift, respectively. HC-2.0 underwent large strength drops from the first cycle up to 6% drift, and completely collapsed during the 7% drift cycles, owing to rupture of the diagonal reinforcement. On the other hand, HC-3.5 started to become unstable only from the 10% drift cycles. The ductility ratios of Specimens HC-2.0 and HC-3.5 for loading in the positive direction were approximately 3.7 and 5.6, respectively.
It is noted that the normalized shear stress greatly exceeded the design limit of 0.83 for diagonally reinforced coupling beams as specified in section 18.10.7.4(a) of ACI 318-14 (2014). Therefore, the test results suggest that bundled diagonal reinforcement was applicable in both deep and slender coupling beams, and that the HPFRCC was effective in allowing the amount of transverse reinforcement required by section 18.10.7.4(d) in ACI 318-14 to be reduced by half. It should be noted that the measured strengths of all the specimens in the tests are significantly larger than the calculated strengths per ACI 318-14. This is on agreement with the results of previous studies (Lequesne et al. 2010; Han et al. 2015). Such overstrength must be accounted for in the seismic design of diagonally reinforced coupling beam themselves and also adjoining walls. Otherwise, significant damage could not be avoided in adjoining walls during design-level earthquakes.
4 Cyclic Deterioration, Energy Dissipation, and Shear Distortion
4.1 Strength and Stiffness Degradations
Figure 11 shows the envelopes of the cyclic shear-drift response curves for the four coupling beam specimens. Among both pairs of specimens with the same aspect ratio, the RC and HPFRCC specimens not only achieved similar maximum loads, but also underwent similar strength degradation histories. In addition, the primary cause of sudden strength drops in all four specimens was the rupture of diagonal reinforcement with no buckling. Therefore, combining the use of HPFRCC and half the amount of code-required transverse steel appeared to provide confinement equivalent to that of the code-required transverse reinforcement. This figure also included the envelop curve for code-compliant specimens RC-ACI-2.0 and RC-ACI-3.5 with distributed diagonal bars. It is observed that the envelop curves of RC-ACI specimens with distributed diagonal reinforcement were close to those of corresponding RC and HPFRCC specimens with bundled diagonal bars.
Figure 12 shows the stiffness degradation histories of the four specimens, from which the degree of stiffness retention can be assessed. The normalized stiffness in the vertical axis was determined by dividing the stiffness of the specimen during the first cycle (of two consecutive cycles) under a given drift by the initial stiffness in the first cycle under 0.25% drift. The stiffness of the specimen during a loading cycle was taken to be the slope of the line connecting the two points at the positive and negative peak drifts on the load–displacement curve (i.e., peak-to-peak stiffness) as illustrated in Fig. 12.
For both pairs of specimens having the same aspect ratio, the RC and HPFRCC specimens exhibited similar stiffness retention capacities throughout the tests, although the stiffness retention capacity of HPFRCC specimens appeared to be slightly better than RC specimens. HPFRCC specimens also had similar stiffness retention capacity to RC specimen with distributed diagonal reinforcement.
4.2 Energy Dissipation
Energy dissipation capacity was investigated among the four specimens subjected to the same loading history. In general, higher energy dissipation corresponds to better seismic resistance. Figure 13 presents cumulative energy dissipation for the four specimens. The amount of energy dissipated during a loading cycle was taken as the area surrounded by the load–displacement curve for the cycle; see illustration in Fig. 13. The accumulated energy in the vertical axis of Fig. 13 is the sum of dissipated energy in all cycles up to the indicated drift.
Between the two deep coupling beam specimens, the HC-2.0 specimen dissipated consistently larger amounts of energy, with about 20% greater energy dissipation than RC-2.0 (RC-ACI-2.0) up to the 7% drift cycles (Fig. 13a), even though its transverse reinforcement had been reduced by 50%. In contrast, the two slender specimens, RC-3.5 and HC-3.5, dissipated very similar amount of energy up to 10% drift (Fig. 13b). They dissipated more energy than specimen RC-ACI-2.0 with distributed diagonal bars. At a given drift, dissipated energy was much larger in the deep specimens than in the slender specimens because of the greater strength of deep specimens. Note that the inclination angle of the diagonal bars in the deep coupling beams (l n /h = 2.0) was larger than that in the slender coupling beams (l n /h = 3.5).
4.3 Shear Deformation
The degree of shear cracking damage in a specimen was quantified by the amount of shear deformation. The shear deformation of the specimen was assessed by using the data acquired from the LVDTs installed at one side face of the coupling beam (D1–D2, L1–L4 for the deep beams as illustrated in Fig. 5a, and D1–D4, L1–L4, L9–L12 for the slender beams as illustrated in Fig. 5b). For each shaded region shown in Fig. 14, the average shear deformation γ was estimated as follows:
Here, γ1 and γ2 are the angular changes in the two initially 90°angles of each shaded region (e.g., at points 2 and 3 in Fig. 5c). The angular changes were estimated by using the deformed lengths of the two initially right triangles (having a common hypotenuse, e.g., between points 1 and 4) formed by the LVDTs. It was assumed that during testing there was no change in length along the transverse axis of the beam (e.g., between points 1 and 2, and between points 3 and 4 in Fig. 5c).
Figure 14 presents the shear distortion responses of all four specimens up to the 5% drift cycles, plotted with respect to the lateral load. Regardless of the length-to-depth aspect ratio (l n /h), the HPFRCC specimens generally underwent less shear distortion than the RC specimens, even though the HPFRCC specimens had 50% less transverse reinforcement. This is in accordance with the results that the RC specimens suffered more intensive shear cracking damage than the HPFRCC specimens. This suggests that the HPFRCC was effective in bridging shear cracks to control the crack widths.
In the specimens of aspect ratio 2.0, the peak shear distortion occurring during the 2% drift cycles was about 0.007 and 0.002 rad in RC-2.0 and HC-2.0, respectively, that occurring during the 5% drift cycles was about 0.028 and 0.010 rad in RC-2.0 and HC-2.0, respectively. At each drift level, the shear distortion in HC-2.0 was less than about 1/3 that of RC-2.0. In the specimens of aspect ratio 3.5, the beam ends generally suffered larger shear distortions than the middle parts, which was not the case in the specimens of aspect ratio 2.0. During the 5% drift cycles, Specimens RC-3.5 and HC-3.5 had the peak shear distortions of about 0.027 and 0.009 rad at the ends of the beams.
5 Conclusions
In this study, experimental tests were conducted to assess the cyclic behavior of HPFRCC coupling beams with bundled diagonal reinforcement and widely spaced transverse reinforcement. Their cyclic performance was compared with that of concrete coupling beams with bundled and distributed diagonal bars and full amount transverse reinforcement required in ACI 318-14 as well as that of code-compliant concrete coupling beams (RC-ACI) with distributed diagonal bars and full amount of transverse reinforcement. Both deep (l n /h = 2.0) and slender (l n /h = 3.5) coupling beams were considered. Important findings and conclusions are summarized as follows:
-
(1)
The HPFRCC coupling beams had similar lateral strengths to those of the RC coupling beams and superior seismic capacities (e.g., ductility, energy dissipation), even though the HPFRCC specimens had bundled diagonal reinforcement and only half the code-required amount of transverse reinforcement. This suggests that the amount of transverse reinforcement required by ACI 318-14 (ACI 2014) could be reduced by half with the use of HPFRCC, which supplied adequate confinement for the bundled diagonal bars. Moreover, distributed diagonal reinforcement can be replaced by bundled diagonal reinforcement.
-
2.
Concrete coupling beam specimens RC-2.0 (l n /h = 2.0) and RC-3.5 (l n /h = 3.5), which had bundled diagonal reinforcement, achieved the maximum drift ratio of about 5.37 and 10.04, respectively. Also, no substantial strength drop occurred until the bundled diagonal bars ruptured in these specimens. This indicates that the use of bundled diagonal reinforcement was effective in ensuring suitable seismic performances of both deep and slender coupling beams; this design also enables simplified construction.
-
3.
HPFRCC specimens HC-2.0 and HC-3.5 having bundled diagonal reinforcement and half the transverse reinforcement required in ACI 318-14 produced the maximum drift ratio of about 5.98 and 10.79, respectively. Therefore, the superior seismic performance of coupling beams can be maintained by using HPFRCC, bundled diagonal reinforcement and reduced transverse reinforcement.
-
4.
In all specimens studied in the present work, the coupling beam portion was precast first, and the stubs at the ends of the beam that represented in situ shear walls were constructed later, allowing cold joints between the beam and stubs. Nevertheless, none of these specimens experienced sliding at the beam-stub interfaces during the tests. This implies that the bundled diagonal reinforcement provided sufficient friction shear strength to resist sliding. Therefore, precast construction of these concrete coupling beams turned out to be feasible.
References
ACI Committee 318. (2014). Building code requirements for structural concrete and commentary. ACI 318-14 and ACI 318R-14, American Concrete Institute, Farmington Hills, Mich., USA.
Barbachyn, S. M., Kurama, Y. C., & Novak, L. C. (2012). Analytical evaluation of diagonally reinforced concrete coupling beams under lateral loads. ACI Structural Journal, 109(4), 497–508.
Barney, G. B., Shiu, K. N., Rabbit, B. G., Fiorato, A. E., Russell, H. G., & Corley, W. G. (1980). Behavior of coupling beams under load reversals (RD068. 01B). Skokie, IL: Portland Cement Association.
Canbolat, B. A., Parra-Montesinos, G. J., & Wight, J. K. (2005). Experimental study on seismic behavior of high-performance fiber-reinforced cement composite coupling beams. ACI Structural Journal, 102(1), 159–166.
Comité Européen de Normalization (CEN). (2004). Eurocode 8: Design of structures for earthquake resistance—Part 1: General rules, seismic actions and rules for buildings. EN 1998-1-1, Brussels.
Fortney, P. J., Rassati, G. A., & Shahrooz, B. M. (2008). Investigation on effect of transverse reinforcement on performance of diagonally reinforced coupling beams. ACI Structural Journal, 105(6), 781–788.
Galano, L., & Vignoli, A. (2000). Seismic behavior of short coupling beams with different reinforcement layouts. ACI Structural Journal, 97(6), 876–885.
Han, S. W., Lee, C. S., Shin, M., & Lee, K. (2015). Cyclic performance of precast coupling beams with bundled diagonal reinforcement. Engineering Structures, 93, 142–151.
Harries, K. A., Fortney, P. J., Shahrooz, B. M., & Brienen, P. J. (2005). Practical design of diagonally reinforced concrete coupling beams-critical review of ACI 318 requirements. ACI Structural Journal, 102(6), 876–882.
Kim, J. S., Kim, Y. Y., & Kim, J. K. (2007). Diverse application of ECC designed with ground granulated blast furnace slag. International Journal of Concrete Structures and Materials, 1(1), 11–18.
Kim, D. J., Naaman, A. E., & El-Tawil, S. (2009). High performance fiber reinforced cement composites with innovative slip hardending twisted steel fibers. International Journal of Concrete Structures and Materials, 3(2), 119–126.
Lequesne, R. D., Setkit, M., Parra-Montesinos, G. J., & Wight, J. K. (2010). Seismic detailing and behavior of coupling beams with high-performance fiber reinforced concrete. In Symposium–Four decades of progress in prestressed concrete, fiber reinforced concrete, and thin laminate composites. American Concrete Institute, Farmington Hills, MI, SP-272, 205-222.
Li, V. C. (2003). On engineered cementitious composites (ECC). Journal of advanced concrete technology, 1(3), 215–230.
Li, V. C. (2012). Tailoring ECC for special attributes: A review. International Journal of Concrete Structures and Materials, 6(3), 135–144.
MacGregor, J. K., & Wight, J. G. (2009). Reinforced concrete: Mechanics and design (5th ed.). Upper Saddle River, NJ: Prentice Hall.
Naaman, A. E. (2003). Engineered steel fibers with optimal properties for reinforcement of cement composites. Journal of advanced concrete technology, 1(3), 241–252.
Naaman, A. E., Likhitruangsilp, V., & Parra-Montesinos, G. J. (2007). Punching shear response of high-performance fiber-reinforced cementitious composite slabs. ACI Structural Journal, 104(2), 170–179.
Naish, D., Fry, A., Klemencic, R., & Wallace, J. (2013). Reinforced concrete coupling beams-Part I: Testing. ACI Structural Journal, 110(6), 1057–1066.
New Zealand Standard (NZS). (1982). New Zealand standard code of practice for the design of concrete structures. NZS 3101, Standard Association of New Zealand, Wellington, New Zealand.
Olsen, E. C., & Billington, S. L. (2011). Cyclic response of precast high-performance fiber-reinforced concrete infill panels. ACI Structural Journal, 108(1), 51–60.
Pan, A., & Moehle, J. P. (1989). Lateral displacement ductility of reinforced concrete flat plates. ACI Structural Journal, 86(3), 250–258.
Parra-Montesinos, G. J. (2005). High-performance fiber-reinforced cement composites: an alternative for seismic design of structures. ACI Structural Journal, 102(5), 668–675.
Parra-Montesinos, G. J., Peterfreund, S. W., & Chao, S. H. (2005). Highly damage-tolerant beam-column joints through use of high-performance fiber-reinforced cement composites. ACI Structural Journal, 102(3), 487–495.
Paulay, T. (1971). Coupling beams of reinforced concrete shear walls. Journal of the Structural Division, 97(3), 843–862.
Paulay, T., & Binney, J. R. (1974). Diagonally reinforced coupling beams of shear walls. ACI Special Publication, 42, 579–598.
Paulay, T., & Priestley, M. J. (1992). Seismic design of reinforced concrete and masonry buildings. N.Y.: John Wiley & Sons.
Shin, M., Gwon, S. W., Lee, K., Han, S. W., & Jo, Y. W. (2014). Effectiveness of high performance fiber-reinforced cement composites in slender coupling beams. Construction and Building Materials, 68, 476–490.
Tassios, T. P., Moretti, M., & Bezas, A. (1996). On the behavior and ductility of reinforced concrete coupling beams of shear walls. ACI Structural Journal, 93(6), 711–720.
Wallace, J. W. (2012). Behavior, design, and modeling of structural walls and coupling beams—Lessons from recent laboratory tests and earthquakes. International Journal of Concrete Structures and Materials, 6(1), 3–18.
Acknowledgements
Authors acknowledge the financial supports provided by the National research foundation of Korea (NRF-2017R1A2B3008937).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Han, S.W., Kang, JW., Jee, HW. et al. Cyclic Behavior of HPFRCC Coupling Beams with Bundled Diagonal Bars. Int J Concr Struct Mater 12, 42 (2018). https://doi.org/10.1186/s40069-018-0271-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40069-018-0271-6