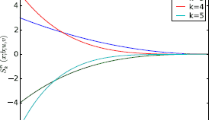Certain results on a hybrid class of the Boas–Buck polynomials

Abstract

This article aims to introduce a hybrid family of 2-variable Boas–Buck-general polynomials by taking Boas–Buck polynomials as a base with the 2-variable general polynomials. These polynomials are framed within the context of the monomiality principle, and their properties are established. Further, we investigate some members belonging to this family. A general method to express connection coefficients explicitly for the Boas–Buck general polynomial sets is presented. Carlitz theorem for mixed generating functions is also extended to these polynomials. The shapes are shown and zeros are computed for these polynomials using Mathematica software.

1 Introduction and preliminaries

Special functions of multivariable form have shown remarkable progress in recent years [1–6]. These functions arise in diverse areas of mathematics, and they provide a new means of analysis ranging from the solution of large classes of partial differential equations often encountered in physical problems to the abstract group theory. A hybrid class of polynomials exhibits a nature lying between the two polynomial families, which are introduced and studied employing appropriate operational rules [7–14].

To consider the convolution of two or more polynomials to introduce new multivariable generalized polynomials is a recent topic of research and is useful from the point of view of applications. These multivariable hybrid special polynomials are important as they possess significant properties. It is useful from an applicative point of view and appears in certain problems of number theory, combinatorics, classical and numerical analysis, theoretical physics, approximation theory, and other fields of pure and applied mathematics.

We recall the following 2-variable form of special polynomials, namely 2-variable general polynomials.

Definition 1.1

A general polynomial set is said to be 2-variable general polynomials $P_{n}(x,y)$ if it has the following generating function [1]:

$$ e^{xt}\varPhi (y,t)= \sum_{n=0}^{\infty }P_{n}(x,y) \frac{t^{n}}{n!}, \qquad P_{0}(x,y)=1, $$

(1)

where $\varPhi (y,t)$ has (at least the formal) series expansion

$$ \varPhi (y,t)=\sum_{n=0}^{\infty } \phi _{n}(y)\frac{t^{n}}{n!},\qquad \phi _{0}(y)\neq 0. $$

(2)

The 2-variable general polynomials family contains many important polynomials. We present the list of some known 2-variable general polynomial families in Table 1.

Table 1 Certain members belonging to the 2-variable general polynomials $P_{n}(x,y)$

The Boas–Buck polynomial set was introduced by Boas and Buck [15] in the year 1956. It includes many important general classes of polynomial sets like Brenke polynomials, Sheffer polynomials, Appell polynomials, etc. The Boas–Buck polynomial set is defined by means of generating function as follows.

Definition 1.2

A polynomial set is said to be Boas–Buck polynomial set if it has the following generating function [15]:

$$ A(t)B\bigl(xC(t)\bigr)=\sum_{n=0}^{\infty }F_{n}(x) \frac{t^{n}}{n!}, $$

(3)

where A, B, and C are the power series such that

$$\begin{aligned}& A(t) = \sum_{n=0}^{\infty }a_{n} \frac{t^{n}}{n!},\quad a_{0} \neq 0; \end{aligned}$$

(4)

$$\begin{aligned}& B(t) = \sum_{n=0}^{\infty }b_{n} \frac{t^{n}}{n!},\quad b_{n} \neq 0 \text{ for all } n; \end{aligned}$$

(5)

$$\begin{aligned}& C(t) = \sum_{n=1}^{\infty }c_{n} \frac{t^{n}}{n!},\quad c_{1} \neq 0. \end{aligned}$$

(6)

The Boas–Buck polynomial set defined by Equation (3) is quasi-monomial under the action of the following multiplicative and derivative operators [16]:

$$\begin{aligned}& \hat{M}_{F} = xD_{x}C^{\prime } \bigl(C^{-1}(\sigma )\bigr)\sigma ^{-1}+ \frac{A^{\prime }(C^{-1}(\sigma ))}{A(C^{-1}(\sigma ))}, \end{aligned}$$

(7)

$$\begin{aligned}& \hat{P}_{F} = C^{-1}(\sigma ), \end{aligned}$$

(8)

where σ is the derivative operator of $B_{n}(x)=\sum_{k=0}^{n}b_{k}\frac{x^{k}}{k!}$ and is given by

$$ \sigma (1)=0\quad \text{and}\quad \sigma \bigl(x^{n} \bigr)= n \frac{b_{n-1}}{b_{n}}x^{n-1},\quad n=1,2,\ldots . $$

(9)

According to the monomiality principle, the multiplicative operator $\hat{M}_{F}$ and derivative operator $\hat{P}_{F}$ of Boas–Buck polynomials $F_{n}(x)$, when acting on the Boas–Buck polynomials $F_{n}(x)$, yield

$$ \hat{M}_{F} \bigl\{ F_{n}(x)\bigr\} =F_{n+1}(x) $$

(10)

and

$$ \hat{P}_{F} \bigl\{ F_{n}(x)\bigr\} =nF_{n-1}(x). $$

(11)

The differential equation satisfied by Boas–Buck polynomials $F_{n}(x)$ is given by

$$ \hat{M}_{F}\hat{P}_{F}\bigl\{ F_{n}(x)\bigr\} =nF_{n}(x). $$

(12)

The exponential generating function of Boas–Buck polynomials $F_{n}(x)$ can be cast in the form

$$ \exp (\hat{M}_{F} t)\{1\}=\sum _{n=0}^{\infty }F_{n}(x) \frac{t^{n}}{n!}. $$

(13)

The Boas–Buck polynomial set includes many important general classes of polynomial sets. Some of them are listed in Table 2.

Table 2 Certain members belonging to the Boas–Buck family

In this paper, the 2-variable Boas–Buck-general polynomials are introduced by means of a generating function, and their properties are studied. In order to show some applications of the main results, several illustrative examples are also considered. The Carlitz theorem for mixed generating functions is extended to the 2-variable Boas–Buck-general polynomials, and an alternative method for finding the connection coefficient between two 2-variable Boas–Buck-general polynomials is also presented. A recursion relation characterizing the 2-variable Boas–Buck-general polynomials is derived. Certain graphical representations and numerical computations for these polynomials are also presented.

2 Boas–Buck-general polynomials ${}_{F}P_{n}(x,y)$

In this section, a new hybrid class of the 2-variable Boas–Buck-general polynomials (2VBBGP) denoted by ${}_{F}P_{n}(x,y)$ is introduced by convoluting the Boas–Buck polynomials $F_{n}(x)$ and 2-variable general polynomials $P_{n}(x,y)$. In order to establish the generating function for these polynomials, the operational technique with monomiality principle plays a major role. Indeed, on replacing x by the multiplicative operator $\hat{M}_{F}$ (7) of the Boas–Buck polynomials $F_{n}(x)$ in the generating function (1) of the 2-variable general polynomials $P_{n}(x,y)$, the following expression is obtained:

$$ \exp (\hat{M}_{F} t)\varPhi (y,t)= \sum _{n=0}^{\infty }P_{n}(\hat{M}_{F},y) \frac{t^{n}}{n!}. $$

(14)

Using Equation (13) (for 2VBBGP ${}_{F}P_{n}(x,y)$) and denoting $P_{n}(\hat{M}_{F},y)$ by the resultant 2-variable Boas–Buck-general polynomials (2VBBGP) ${}_{F}P_{n}(x,y)$, we get

$$ \varPhi (y,t)\sum_{n=0}^{\infty }F_{n}(x) \frac{t^{n}}{n!}=\sum_{n=0}^{ \infty } \,{}_{F}P_{n}(x,y)\frac{t^{n}}{n!}, $$

(15)

which by virtue of Equation (3) gives the following generating function of 2VBBGP ${}_{F}P_{n}(x,y)$:

$$ \varPhi (y,t) A(t)B\bigl(xC(t)\bigr)=\sum _{n=0}^{\infty } \,{}_{F}P_{n}(x,y) \frac{t^{n}}{n!}. $$

(16)

Further, using expansion (2) in Equation (15), then simplifying and comparing similar powers of t on both sides of the resultant equation, we get the following series expansion of the 2VBBGP ${}_{F}P_{n}(x,y)$:

$$ {}_{F}P_{n}(x,y)=\sum _{k=0}^{n}{}^{n}C_{k} F_{n-k}(x) \phi _{k}(y). $$

(17)

In view of Table 2, certain polynomial sets belonging to the 2-variable Boas–Buck-general family ${}_{F}P_{n}(x,y)$ are established and mentioned in Table 3.

Table 3 Certain members belonging to the 2VBBGP ${}_{F}P_{n}(x,y)$

In order to ensure that the 2VBBGP ${}_{F}P_{n}(x,y)$ are quasi-monomial, the following result is proved. For the sake of uniformity, throughout the paper we take

$$ \varPhi ^{\prime }(y,z)=\frac{\partial }{\partial z}\varPhi (y,z), $$

(18)

unless otherwise stated.

Theorem 2.1

The multiplicative and derivative operators of 2VBBGP${}_{F}P_{n}(x,y)$are respectively given by

$$ \hat{M}_{{}_{F}P}=x\partial _{x}C^{\prime } \bigl(C^{-1}(\sigma )\bigr)\sigma ^{-1} + \frac{A^{\prime }(C^{-1}(\sigma ))}{A(C^{-1}(\sigma ))}+ \frac{\varPhi ^{\prime }(y,C^{-1}(\sigma ))}{\varPhi (y,C^{-1}(\sigma ))} $$

(19)

and

$$ \hat{P}_{{}_{F}P}=C^{-1}(\sigma ). $$

(20)

Proof

Note that Equation (9) allows us to write the relation

$$ \sigma B (xt)=t B (xt). $$

(21)

So that we can write

$$ C^{-1}(\sigma ) \varPhi (y,t) A(t)B\bigl(xC(t)\bigr)=t \varPhi (y,t) A(t)B\bigl(xC(t)\bigr). $$

(22)

Differentiating Equation (16) partially with respect to t, we obtain

$$ \biggl[ x\partial _{x}\frac{C^{\prime }(t)}{C(t)}+ \frac{A^{\prime }(t)}{A(t)}+ \frac{\varPhi ^{\prime }(y,t)}{\varPhi (y,t)} \biggr] \sum_{n=0}^{\infty }\,{}_{F}P_{n}(x,y) \frac{t^{n}}{n!}=\sum_{n=0}^{ \infty }\,{}_{F}P_{n+1}(x,y) \frac{t^{n}}{n!}. $$

(23)

Now, using identity (22) and comparing similar powers of t gives

$$ \biggl[ x \partial _{x} C^{\prime }\bigl(C^{-1}( \sigma )\bigr)\sigma ^{-1}+ \frac{A^{\prime }(C^{-1}(\sigma ))}{A(C^{-1}(\sigma ))}+ \frac{\varPhi ^{\prime }(y,C^{-1}(\sigma ))}{\varPhi (y,C^{-1}(\sigma ))} \biggr] \,{}_{F}P_{n}(x,y)=\,{}_{F}P_{n+1}(x,y), $$

(24)

which in view of relation (10) (for 2VBBGP ${}_{F}P_{n}(x,y)$) gives assertion (19).

Rewriting identity (22) using generating function (16) of 2VBBGP ${}_{F}P_{n}(x,y)$, we obtain

$$ C^{-1}(\sigma )\sum_{n=0}^{\infty } \,{}_{F}P_{n}(x,y)\frac{t^{n}}{n!}= \sum _{n=1}^{\infty } n \,{}_{F}P_{n-1}(x,y) \frac{t^{n}}{n!}, $$

(25)

which on comparing similar powers of t and in view of relation (11) (for 2VBBGP ${}_{F}P_{n}(x,y)$) gives assertion (20). □

In view of relation (12) (for 2VBBGP ${}_{F}P_{n}(x,y)$), expressions (19) and (20) give the following result.

Theorem 2.2

The 2VBBGP${}_{F}P_{n}(x,y)$satisfies the following differential equation:

$$ \biggl[x\partial _{x}C^{\prime } \bigl(C^{-1}(\sigma )\bigr)\sigma ^{-1}-nC( \sigma ) + \frac{A^{\prime }(C^{-1}(\sigma ))}{A(C^{-1}(\sigma ))}+ \frac{\varPhi ^{\prime }(y,C^{-1}(\sigma ))}{\varPhi (y,C^{-1}(\sigma ))} \biggr] \,{}_{F}P_{n}(x,y)=0. $$

(26)

Remark 2.1

Taking $C(t)=t$ in Equations (19), (20), and (26), the following consequences of Theorems 2.1 and 2.2 are deduced.

Corollary 2.1

The Brenke general polynomials${}_{Y}P_{n}(x,y)$are quasi-monomial with respect to the following multiplicative and derivative operators:

$$\begin{aligned}& \hat{M}_{{}_{Y}P} = x\partial _{x}\sigma ^{-1} + \frac{A^{\prime }(\sigma )}{A(\sigma )}+ \frac{\varPhi ^{\prime }(y,\sigma )}{\varPhi (y,\sigma )}, \end{aligned}$$

(27)

$$\begin{aligned}& \hat{P}_{{}_{Y}P} = \sigma \end{aligned}$$

(28)

and satisfy the following differential equation:

$$ \biggl[x\partial _{x}\sigma ^{-1}-n\sigma + \frac{A^{\prime }(\sigma )}{A(\sigma )}+ \frac{\varPhi ^{\prime }(y,\sigma )}{\varPhi (y,\sigma )} \biggr] \,{}_{Y}P_{n}(x,y) =0. $$

(29)

Remark 2.2

Taking $B(t)=\exp (t)$ in Equations (19), (20), and (26), the following consequences of Theorems 2.1 and 2.2 are deduced.

Corollary 2.2

The Sheffer general polynomials${}_{S}P_{n}(x,y)$are quasi-monomial with respect to the following multiplicative and derivative operators:

$$\begin{aligned}& \hat{M}_{{}_{S}P} = xC^{\prime }\bigl(C^{-1}(\partial _{x})\bigr) + \frac{A^{\prime }(C^{-1}(\partial _{x}))}{A(C^{-1}(\partial _{x}))} + \frac{\varPhi ^{\prime }(y,C^{-1}(\partial _{x}))}{\varPhi (y,C^{-1}(\partial _{x}))}, \end{aligned}$$

(30)

$$\begin{aligned}& \hat{P}_{{}_{S}P} = C^{-1}(\partial _{x}) \end{aligned}$$

(31)

and satisfy the following differential equation:

$$ \biggl[xC^{\prime }\bigl(C^{-1}(\partial _{x}) \bigr)-nC(\partial _{x}) + \frac{A^{\prime }(C^{-1}(\partial _{x}))}{A(C^{-1}(\partial _{x}))}+ \frac{\varPhi ^{\prime }(y,C^{-1}(\partial _{x}))}{\varPhi (y,C^{-1}(\partial _{x}))} \biggr] \,{}_{S}P_{n}(x,y)=0. $$

(32)

Remark 2.3

Taking $C(t)=t$ and $B(t)=\exp (t)$ in Equations (19), (20), and (26), the following consequences of Theorems 2.1 and 2.2 are deduced.

Corollary 2.3

The Appell general polynomials${}_{L}P_{n}(x,y)$are quasi-monomial with respect to the following multiplicative and derivative operators:

$$\begin{aligned}& \hat{M}_{{}_{L}P} = x + \frac{A^{\prime }(\partial _{x})}{A(\partial _{x})}+ \frac{\varPhi ^{\prime }(y,\partial _{x})}{\varPhi (y,\partial _{x})}, \end{aligned}$$

(33)

$$\begin{aligned}& \hat{P}_{{}_{L}P} = \partial _{x} \end{aligned}$$

(34)

and satisfy the following differential equation:

$$ \biggl[x-n\partial _{x} + \frac{A^{\prime }(\partial _{x})}{A(\partial _{x})}+ \frac{\varPhi ^{\prime }(y,\partial _{x})}{\varPhi (y,\partial _{x})} \biggr] \,{}_{L}P_{n}(x,y)=0. $$

(35)

In the next section, we discuss the illustrative examples of some members belonging to the 2-variable Boas–Buck-general family ${}_{F}P_{n}(x,y)$ in order to give applications of the results derived above.

3 Illustrative examples

Certain polynomial sets belonging to the 2VBBGP ${}_{F}P_{n}(x,y)$ and their corresponding results for the above established properties are derived and mentioned in the following illustrative examples.

Example 3.1

For $\varPhi (y,t)=e^{yt^{s}}$, the 2-variable general polynomials $P_{n}(x,y)$ reduce to the Gould–Hopper polynomials $G^{(s)}_{n}(x,y)$ (Table 1(I)). Consequently, the resulting Boas–Buck–Gould–Hopper polynomials denoted by ${}_{F}G^{(s)}_{n}(x,y)$ are defined by the following generating function:

$$ \exp \bigl(yt^{s}\bigr)A(t)B\bigl(xC(t)\bigr)=\sum _{n=0}^{\infty }\,{}_{F}G^{(s)}_{n}(x,y) \frac{t^{n}}{n!}. $$

(36)

The other corresponding results for Boas–Buck–Gould–Hopper polynomials ${}_{F}G^{(s)}_{n}(x,y)$ are presented in Table 4.

Table 4 Results for Boas–Buck–Gould–Hopper polynomials ${}_{F}G^{(s)}_{n}(x,y)$

Remark 3.1

Since for $s=2$ the Gould–Hopper polynomials $G_{n}^{(s)}(x,y)$ reduce to the 2-variable Hermite Kampé de Feriet polynomials $H_{n}(x,y)$, taking $s=2$ in Equation (36), we get the following generating function for the Boas–Buck–Hermite polynomials denoted by ${}_{F}H_{n}(x,y)$:

$$ \exp \bigl(yt^{2}\bigr)A(t)B\bigl(xC(t)\bigr)=\sum _{n=0}^{\infty }\,{}_{F}H_{n}(x,y) \frac{t^{n}}{n!}. $$

(37)

The series definition and other results for the Boas–Buck–Hermite polynomials ${}_{F}H_{n}(x, y)$ can be obtained by taking $s=2$ in the results given in Table 4.

Example 3.2

For $\varPhi (y,t)=C_{0}(-yt^{s})$, the 2-variable general polynomials $P_{n}(x,y)$ reduce to the 2-variable generalized Laguerre polynomials ${{}_{s}L_{n}(y,x)}$ (Table 1(II)). Consequently, the resulting Boas–Buck–generalized Laguerre polynomials denoted by ${}_{F}L^{(s)}_{n}(x,y)$ are defined by the following generating function:

$$ C_{0}\bigl(-yt^{s}\bigr)A(t)B \bigl(xC(t)\bigr)=\sum_{n=0}^{\infty }\,{}_{F}L^{(s)}_{n}(x,y) \frac{t^{n}}{n!}. $$

(38)

The other corresponding results for Boas–Buck-generalized Laguerre polynomials ${}_{F}L^{(s)}_{n}(x,y)$ are presented in Table 5.

Table 5 Results for Boas–Buck-generalized Laguerre polynomials ${}_{F}L^{(s)}_{n}(x,y)$

Remark 3.2

Since for $s=1$ and $y\rightarrow -y$ the 2-variable generalized Laguerre polynomials ${{}_{s}}L_{n}(y,x)$ reduce to the 2-variable Laguerre polynomials $L_{n}(y,x)$, taking $s=1$ and $y\rightarrow -y$ in Equation (38), we get the generating function for the Boas–Buck–Laguerre polynomials denoted by ${}_{F}L_{n}(x,y)$:

$$ C_{0}(yt)A(t)B\bigl(xC(t)\bigr)=\sum_{n=0}^{\infty }\,{}_{F}L_{n}(x,y) \frac{t^{n}}{n!}. $$

(39)

The series definition and other results for the Boas–Buck–Laguerre polynomials ${}_{F}L_{n}(x,y)$ can be obtained by taking $s=1$ and $y\rightarrow -y$ in the results given in Table 5.

Example 3.3

For $\varPhi (y,t)=\frac{1}{1-yt^{r}}$, the 2-variable general polynomials $P_{n}(x,y)$ reduce to the 2-variable truncated exponential polynomials of order r, $e_{n}^{(r)}(x,y)$ (Table 1(III)). Consequently, the resulting Boas–Buck-truncated exponential polynomials of order r denoted by ${}_{F}e^{(r)}_{n}(x,y)$ are defined by the following generating function:

$$ \frac{1}{1-yt^{r}}A(t)B\bigl(xC(t)\bigr)=\sum_{n=0}^{\infty }\,{}_{F}e^{(r)}_{n}(x,y) \frac{t^{n}}{n!}. $$

(40)

The other corresponding results for Boas–Buck-truncated exponential polynomials of order r${}_{F}e^{(r)}_{n}(x,y)$ are presented in Table 6.

Table 6 Results for Boas–Buck-truncated exponential polynomials ${}_{F}e^{(r)}_{n}(x,y)$

Example 3.4

For $\varPhi (y,t)=\frac{te^{yt^{j}}}{e^{t}-1}$, the 2-variable general polynomials $P_{n}(x,y)$ reduce to the 2-dimensional Bernoulli polynomials $B_{n}^{(j)}(x,y)$ (Table 1(IV)). Consequently, the resulting Boas–Buck–Bernoulli polynomials denoted by ${}_{F}B^{(j)}_{n}(x,y)$ are defined by the following generating function:

$$ \frac{te^{yt^{j}}}{e^{t}-1}A(t)B\bigl(xC(t)\bigr)=\sum_{n=0}^{\infty }\,{}_{F}B^{(j)}_{n}(x,y) \frac{t^{n}}{n!}. $$

(41)

The other corresponding results for Boas–Buck–Bernoulli polynomials ${}_{F}B^{(j)}_{n}(x,y)$ are presented in Table 7.

Table 7 Results for Boas–Buck–Bernoulli polynomials ${}_{F}B^{(j)}_{n}(x,y)$

Example 3.5

For $\varPhi (y,t)=\frac{2e^{yt^{j}}}{e^{t}+1}$, the 2-variable general polynomials $P_{n}(x,y)$ reduce to the 2-dimensional Euler polynomials $E^{(j)}_{n}(x,y)$ (Table 1(V)). Consequently, the resulting Boas–Buck–Euler polynomials denoted by ${}_{F}E^{(j)}_{n}(x,y)$ are defined by the following generating function:

$$ \frac{2e^{yt^{j}}}{e^{t}+1}A(t)B\bigl(xC(t)\bigr)=\sum_{n=0}^{\infty }\,{}_{F}E^{(j)}_{n}(x,y) \frac{t^{n}}{n!}. $$

(42)

The other corresponding results for Boas–Buck–Euler polynomials ${}_{F}E^{(j)}_{n}(x,y)$ are presented in Table 8.

Table 8 Results for Boas–Buck–Euler polynomials ${}_{F}E^{(j)}_{n}(x,y)$

In the next section, connection coefficients between two 2VBBGP ${}_{F}P_{n}(x,y)$ sets are derived. Further, Carlitz theorem is extended for the 2VBBGP ${}_{F}P_{n}(x,y)$.

4 Connection coefficient and Carlitz theorem

In the last few years, popularity and interest in detecting connection coefficients have gained attention as they play a vital role in various situations of pure and applied mathematics, especially in combinatorial analysis, and are used in the computation of physical and chemical properties of the quantum-mechanical system. To express a general method for the derivation of connection coefficients for the 2VBBGP ${}_{F}P_{n}(x,y)$, the following theorem is proved.

Theorem 4.1

Let$\{{}_{F}P_{n}(x,y)\}_{n\geq 0}$with lowering operator$\hat{P}_{{}_{F}P}$and$\{{}_{F}Q_{n}(x,y)\}_{n\geq 0}$with lowering operator$\hat{P}_{{}_{F}Q}$be two polynomial sets of 2VBBGP generated respectively by

$$ \varPhi _{1}(y,t) A_{1}(t)B_{1} \bigl(xC_{1}(t)\bigr)=\sum_{n=0}^{\infty } \,{}_{F}P_{n}(x,y) \frac{t^{n}}{n!} $$

(43)

and

$$ \varPhi _{2}(y,t) A_{2}(t)B_{2} \bigl(xC_{2}(t)\bigr)=\sum_{n=0}^{\infty } \,{}_{F}Q_{n}(x,y) \frac{t^{n}}{n!}. $$

(44)

Then the connection coefficient$C_{m,n}$in

$$ {}_{F}Q_{n}(x,y)=\sum _{m=0}^{n}C_{m,n} \,{}_{F}P_{m}(x,y) $$

(45)

is given by the generating function

$$ \frac{A_{2}(t)\varPhi _{2}(0,t)}{A_{1}(f^{-1}(t))\varPhi _{1}(0,f^{-1}(t))} \frac{f^{-m}(t)}{m!}=\sum _{n=0}^{\infty }C_{m,n}\frac{t^{n}}{n!}, $$

(46)

where$\hat{P}_{{}_{F}Q}=f(\hat{P}_{{}_{F}P})$.

Proof

Using the result [20, p. 416, Theorem 3.1], we can write 2VBBGP ${}_{F}Q_{n}(x,y)$ as

$$ {}_{F}Q_{n}(x,y)=\sum _{m=0}^{n}( \hat{P}_{{}_{F}P}) ^{m}{} \frac{{}_{F}Q_{n}(0,0)}{A_{1}(\hat{P}_{{}_{F}P})\varPhi _{1}(0,\hat{P}_{{}_{F}P})} \frac{{}_{F}P_{m}(x,y)}{m!}. $$

(47)

Putting value of ${}_{F}Q_{n}(x,y)$ from Equation (47) in (45) gives

$$ C_{m,n}=\frac{( \hat{P}_{{}_{F}P})^{m}}{m!} \frac{ {}_{F}Q_{n}(0,0)}{A_{1}(\hat{P}_{{}_{F}P})\varPhi _{1}(0,\hat{P}_{{}_{F}P})}. $$

(48)

Since

$$ B_{n}^{(2)}(t)=\sum_{k=0}^{n}b^{(2)}_{k} \frac{t^{k}}{k!}, \quad b_{n} \neq 0 \text{ for all } n, $$

(49)

so, from the result [20, p. 415, Lemma 2.2], we can write

$$ {}_{F}Q_{n}(0,0)=A_{2}( \hat{P}_{{}_{F}Q})\varPhi _{2}(0,\hat{P}_{{}_{F}Q})B^{(2)}_{n}(0). $$

(50)

Using the above relation and the fact $\hat{P}_{{}_{F}Q}=f(\hat{P}_{{}_{F}P})$ in Equation (48), we get

$$ C_{m,n}=f^{-m}( \hat{P}_{{}_{F}Q}) \frac{ A_{2}(\hat{P}_{{}_{F}Q})\varPhi _{2}(0,\hat{P}_{{}_{F}Q})}{A_{1} (f^{-1}(\hat{P}_{{}_{F}Q}))\varPhi _{1}(0,f^{-1}(\hat{P}_{{}_{F}Q}))} \frac{B^{(2)}_{n}(0)}{m!}. $$

(51)

Putting

$$ f^{-m}( t) \frac{ A_{2}(t)\varPhi _{2}(0,t)}{A_{1}(f^{-1}(t))\varPhi _{1}(0,f^{-1}(t))}= \sum _{k=0}^{\infty }g_{k}(m)t^{k} $$

(52)

in Equation (51), we obtain

$$ C_{m,n}=\sum_{k=0}^{\infty }g_{k}(m) (\hat{P}_{{}_{F}Q})^{k} \frac{B^{(2)}_{n}(0)}{m!}. $$

(53)

Since $\hat{P}_{{}_{F}Q}$ is a lowering operator of ${}_{F}Q_{n}(x,y)$, so $\hat{P}_{{}_{F}Q}$ is also a lowering operator of $B_{n}^{(2)}(x)$. Using this fact and simplifying Equation (53) give

$$ C_{m,n}=\frac{n!}{m!}g_{n}(m). $$

(54)

Now, on putting the above value of $g_{n}(m)$ in Equation (52), we obtain assertion (46). □

Remark 4.1

Since for $B_{1}(t)=B_{2}(t)=B(t)$

$$ \hat{P}_{{}_{F}P}=C_{1}^{-1}( \sigma ) $$

(55)

and

$$ \hat{P}_{{}_{F}Q}=C_{2}^{-1}( \sigma ), $$

(56)

where σ is the derivative operator of $B_{n}(x)=\sum_{k=0}^{n}b_{k}\frac{x^{k}}{k!}$, from Equations (55) and (56) we can write

$$ \hat{P}_{{}_{F}Q}=C_{2}^{-1} \bigl(C_{1} (\hat{P}_{{}_{F}P})\bigr). $$

(57)

Thus the following consequence of Theorem 4.1 is obtained.

Corollary 4.1

Let$\{{}_{F}P_{n}(x,y)\}_{n\geq 0}$with lowering operator$\hat{P}_{{}_{F}P}$and$\{{}_{F}Q_{n}(x,y)\}_{n\geq 0}$with lowering operator$\hat{P}_{{}_{F}Q}$be two polynomial sets of 2VBBGP generated respectively by

$$ \varPhi _{1}(y,t) A_{1}(t)B\bigl(xC_{1}(t) \bigr)=\sum_{n=0}^{\infty } \,{}_{F}P_{n}(x,y) \frac{t^{n}}{n!} $$

(58)

and

$$ \varPhi _{2}(y,t) A_{2}(t)B\bigl(xC_{2}(t) \bigr)=\sum_{n=0}^{\infty } \,{}_{F}Q_{n}(x,y) \frac{t^{n}}{n!}. $$

(59)

Then the connection coefficient$C_{m,n}$in

$$ {}_{F}Q_{n}(x,y)=\sum_{m=0}^{n}C_{m,n} \,{}_{F}P_{m}(x,y) $$

(60)

is given by the generating function

$$ \frac{A_{2}(t)\varPhi _{2}(0,t)}{A_{1}(C_{2}(C_{1}(t)))\varPhi _{1}(0,C_{2}(C_{1}(t)))} \frac{C_{2}^{-m}(C_{1}(t))}{m!}=\sum_{n=0}^{\infty }C_{m,n} \frac{t^{n}}{n!}. $$

(61)

To give an application of the result given in Theorem 4.1, we consider the following example.

Example 4.1

Since for $\varPhi _{1}(y,t)=e^{yt^{s}}$ the 2-variable general polynomials $P_{n}(x,y)$ reduce to Gould–Hopper polynomials $G_{n}^{(s)}(x,y)$ (Table 1(I)) and for $A_{1}(t)=\frac{t}{e^{t}-1}$, $B_{1}(xt)=\exp (xt)$ and $C_{1}(t)=t$, the Boas–Buck polynomials reduce to Bernoulli polynomials [21], the resulting Bernoulli–Gould–Hopper polynomials denoted by ${}_{B}G_{n}^{(s)}(x,y)$ are defined by the following generating function:

$$ \frac{t}{e^{t}-1}\exp \bigl(xt+yt^{s}\bigr)=\sum _{n=0}^{\infty } \,{}_{B}G_{n}^{(s)}(x,y) \frac{t^{n}}{n!}. $$

(62)

Since for $\varPhi _{2}(y,t)=C_{0}(-yt^{r})$ the 2-variable general polynomials $P_{n}(x,y)$ reduce to 2-variable generalized Laguerre polynomials ${}_{r}L_{n}(x,y)$ (Table 1(II)) and for $A_{2}(t)=\frac{2}{e^{t}+1}$, $B_{2}(xt)=\exp (xt)$, and $C_{2}(t)=t$ the Boas–Buck polynomials reduce to Euler polynomials [21], the resulting Euler–Laguerre polynomials denoted by ${}_{E}L_{n}^{(r)}(x,y)$ are defined by the following generating function:

$$ \frac{2C_{0}(-yt^{r}) }{e^{t}+1}\exp (xt)=\sum_{n=0}^{\infty } \,{}_{E}L_{n}^{(r)}(x,y) \frac{t^{n}}{n!}. $$

(63)

Now, by using Theorem 4.1, the connection coefficient in

$$ {}_{E}L_{n}^{(r)}(x,y)=\sum _{m=0}^{n}C_{m,n} \,{}_{B}G_{m}^{(s)}(x,y) $$

(64)

is given by the generating function

$$ -\frac{2(e^{t}-1)}{e^{t}+1}\frac{t^{-(m+1)}}{m!}=\sum_{n=0}^{\infty }C_{m,n} \frac{t^{n}}{n!}. $$

(65)

Similarly, connection coefficients of other members belonging to this family can be obtained.

In order to extend Carlitz theorem for 2VBBGP ${}_{F}P_{n}(x,y)$, we first define a generating function of 2VBBGP of order α, ${}_{F}P_{n}^{(\alpha )}(x,y)$ as follows:

$$ \bigl(\varPhi (y,t)\bigr)^{\alpha } A(t)B\bigl(xC(t)\bigr)= \sum_{n=0}^{\infty } \,{}_{F}P_{n}^{( \alpha )}(x,y) \frac{t^{n}}{n!}, $$

(66)

where $\varPhi (y,t)$, $A(t)$, $B(t)$, and $C(t)$ are given by (2), (4), (5), and (6), respectively.

Next we prove the following result.

Theorem 4.2

Let$A(t)$, $B(t)$, $C(t)$, and$\varPhi (y,t)$be regular in the neighborhood of origin. Then, for arbitraryμ, the following generating function for the 2VBBGP of orderα, ${}_{F}P_{n}^{(\alpha )}(x,y)$holds true:

$$ \sum_{n=0}^{\infty }\,{}_{F}P_{n}^{(\alpha +\mu n)}(x,y) \frac{w^{n}}{n!} = \frac{\varPhi ^{\alpha +1}(y,z)A(z)B(xC(z))}{\varPhi (y,z)-\mu z \varPhi ^{\prime }(y,z)}, $$

(67)

where$w=z(\varPhi (y,t))^{-\mu }$.

Proof

Applying Taylor’s expansion theorem in Equation (66), we get

$$ {}_{F}P_{n}^{(\alpha )}(x,y)=\partial _{t}^{n} \bigl\lbrace \bigl(\varPhi (y,t) \bigr)^{ \alpha } A(t)B\bigl(xC(t)\bigr) \bigr\rbrace \big|_{{t=0}},\qquad \partial _{t} \equiv \frac{\partial }{\partial t} $$

(68)

so that we can also write

$$ {}_{F}P_{n}^{(\alpha +\mu n)}(x,y)= \partial _{t}^{n} \bigl\lbrace \bigl( \varPhi (y,t) \bigr)^{\alpha +\mu n} A(t)B\bigl(xC(t)\bigr) \bigr\rbrace \big|_{{t=0}}. $$

(69)

Taking

$$ f(t)=\bigl(\varPhi (y,t)\bigr)^{\alpha } A(t)B\bigl(xC(t) \bigr) $$

(70)

and

$$ \psi (t)=\bigl(\varPhi (y,t)\bigr)^{\mu }, $$

(71)

then Equation (69) can be written as

$$ {}_{F}P_{n}^{(\alpha +\mu n)}(x,y)= \partial _{t}^{n} \bigl\lbrace f(t) \bigl( \psi (t) \bigr)^{n} \bigr\rbrace \big|_{{t=0}}. $$

(72)

Recall Lagrange’s expansion [22, p. 146]

$$ \frac{f(z)}{1-w\psi ^{\prime }(z)}=\sum_{n=0}^{\infty } \frac{w^{n}}{n!}\partial _{t}^{n} \bigl\lbrace f(t) \bigl(\psi (t)\bigr)^{n} \bigr\rbrace \big|_{{t=0}}, $$

(73)

where the functions $f(t)$ and $\psi (t)$ are regular about the origin and z is given by

$$ z=w\psi (z),\quad \psi (z)\neq 0. $$

(74)

Using Equation (72) in Lagrange’s expansion (73), we have

$$ \frac{f(z)}{1-w\psi ^{\prime }(z)}=\sum_{n=0}^{\infty } \frac{w^{n}}{n!}\,{}_{F}P_{n}^{(\alpha +\mu n)}(x,y)\big|_{{t=0}}, $$

(75)

which in view of Equations (70), (71), and (74) gives assertion (67). □

To give an application of the result given in Theorem 4.2, we consider the following example.

Example 4.2

Consider Boas–Buck–Hermite polynomials ${}_{F}H_{n}(x,y)$ defined by Equation (37). In view of Equation (66), the generating function of Boas–Buck–Hermite polynomials of order α${}_{F}H_{n}^{(\alpha )}(x,y)$ is given by

$$ \exp \bigl(\alpha yt^{2}\bigr)A(t)B\bigl(xC(t)\bigr) =\sum _{n=0}^{\infty }\,{}_{F}H_{n}^{( \alpha )}(x,y) \frac{t^{n}}{n!}. $$

(76)

Then its Carlitz type generating function is given by

$$ \sum_{n=0}^{\infty }\,{}_{F}H_{n}^{(\alpha +\mu n)}(x,y) \frac{w^{n}}{n!} = \frac{\exp (\alpha yz^{2})A(z)B(xC(z))}{1-2\mu y z^{2}}, $$

(77)

where $w=z\exp (-\mu yt^{2})$.

Similarly, a Carlitz type generating function of other members belonging to this family can be obtained.

In the next section, the recursion relation which characterizes the 2VBBGP ${}_{F}P_{n}(x,y)$ is given.

5 Concluding remarks

One of the main results of Boas and Buck [15] is that a necessary and sufficient condition for the polynomials $F_{n}(x)$ to have a generating function of Boas–Buck type is that there exists a sequence of numbers $\alpha _{k}$ and $\beta _{k}$ such that, for $n\geq 1$, the following recursion relation holds:

$$ nF_{n}(x)-xF_{n}^{\prime }(x)=\sum _{k=0}^{n-1}\alpha _{k}F_{n-1-k}(x)+x \sum_{k=0}^{n-1}\beta _{k}F_{n-1-k}^{\prime }(x). $$

(78)

For the hybrid polynomials 2VBBGP ${}_{F}P_{n}(x,y)$, we prove the following analogous result.

Theorem 5.1

For the 2VBBGP${}_{F}P_{n}(x,y)$defined by Equation (16), the following recursion relation holds true for$n\geq 1$:

$$\begin{aligned}& n \,{}_{F}P_{n}(x,y)-x \partial _{x}\,{}_{F}P_{n}(x,y) \\& \quad =\sum_{k=0}^{n-1}{}^{n}C_{k+1} \bigl[\bigl(\mu _{k}(y)+\alpha _{k} \bigr)\,{}_{F}P_{n-1-k}(x,y)+x \xi _{k} \partial _{x}\,{}_{F}P_{n-1-k}(x,y) \bigr], \end{aligned}$$

(79)

where

$$\begin{aligned}& t\frac{A^{\prime }(t)}{A(t)}=\sum_{n=0}^{\infty } \alpha _{n} \frac{t^{n+1}}{(n+1)!}, \end{aligned}$$

(80)

$$\begin{aligned}& t\frac{C^{\prime }(t)}{C(t)}=1+\sum_{n=0}^{\infty } \xi _{n} \frac{t^{n+1}}{(n+1)!}, \end{aligned}$$

(81)

and

$$ t\frac{\varPhi ^{\prime }(y,t)}{\varPhi (y,t)}=\sum_{n=0}^{\infty } \mu _{n}(y) \frac{t^{n+1}}{(n+1)!},\qquad \varPhi ^{\prime }(y,t)= \frac{d}{dt}\varPhi (y,t). $$

(82)

Proof

Consider

$$ G=\varPhi (y,t) A(t)B\bigl(xC(t)\bigr). $$

(83)

Then

$$ \frac{\partial G}{\partial x}=C(t)\varPhi (y,t) A(t)B^{\prime } \bigl(xC(t)\bigr) $$

(84)

and

$$ \frac{\partial G}{\partial t}= \biggl[ \frac{\varPhi ^{\prime }(y,t)}{\varPhi ^{(}y,t)}+ \frac{A^{\prime }(t)}{A(t)} +xC^{ \prime }(t)\frac{B^{\prime }(xC(t))}{B(xC(t))} \biggr] \varPhi (y,t) A(t)B\bigl(xC(t)\bigr). $$

(85)

Eliminating $B(xC(t))$ and $B^{\prime }(xC(t))$ from Equations (83)–(85) gives

$$ t\frac{\partial G}{\partial t}-xt\frac{C^{\prime }(t)}{C(t)} \frac{\partial G}{\partial x}= \biggl[ t \frac{\varPhi ^{\prime }(y,t)}{\varPhi ^{(}y,t)}+t\frac{A^{\prime }(t)}{A(t)} \biggr]G. $$

(86)

In view of Equations (16) and (83), we have

$$ G=\sum_{n=0}^{\infty }\,{}_{F}P_{n}(x,y) \frac{t^{n}}{n!}. $$

(87)

Using Equations (80)–(82) and (87) in Equation (86), we have

$$\begin{aligned}& \sum_{n=0}^{\infty }n \,{}_{F}P_{n}(x,y)\frac{t^{n}}{n!}-x \Biggl[1+ \sum _{n=0}^{\infty }\xi _{n} \frac{t^{n+1}}{(n+1)!} \Biggr] \sum_{n=0}^{ \infty } \frac{\partial }{\partial x}\,{}_{F}P_{n}(x,y) \frac{t^{n}}{n!} \\& \quad = \Biggl[ \sum_{n=0}^{\infty } \mu _{n}(y)\frac{t^{n+1}}{(n+1)!}+\sum_{n=0}^{ \infty } \alpha _{n}\frac{t^{n+1}}{(n+1)!} \Biggr]\sum _{n=0}^{\infty }\,{}_{F}P_{n}(x,y) \frac{t^{n}}{n!}. \end{aligned}$$

(88)

Simplifying Equation (88) gives

$$\begin{aligned}& \sum_{n=1}^{\infty } \bigl[ n \,{}_{F}P_{n}(x,y)-x \,{}_{F}P_{n}^{\prime }(x,y) \bigr] \frac{t^{n}}{n!} \\& \quad =\sum_{n=1}^{\infty }\sum _{k=0}^{n-1}{}^{n}C_{k+1} \bigl[\bigl(\mu _{k}(y)+ \alpha _{k} \bigr)\,{}_{F}P_{n-1-k}(x,y)+x \xi _{k} \,{}_{F}P_{n-1-k}^{\prime }(x,y) \bigr] \frac{t^{n}}{n!}, \end{aligned}$$

(89)

from which, on comparing the coefficients of equal powers of t in Equation (89), we get assertion (79). □

Remark 5.1

Since for $C(t)=t$ the 2VBBGP ${}_{F}P_{n}(x,y)$ reduce to the Brenke general polynomials ${}_{Y}P_{n}(x,y)$, from Equation (81) it follows that $\xi _{k}=0$. Thus the following consequence of Theorem 5.1 is obtained.

Corollary 5.1

For the Brenke general polynomials${}_{Y}P_{n}(x,y)$defined by Table 3(I), the following recursion relation holds true for$n\geq 1$:

$$ n \,{}_{F}P_{n}(x,y)-x \partial _{x}\,{}_{F}P_{n}(x,y)=\sum _{k=0}^{n-1}{}^{n}C_{k+1} \bigl( \mu _{k}(y)+\alpha _{k}\bigr)\,{}_{F}P_{n-1-k}(x,y), $$

(90)

where$\alpha _{n}$and$\mu _{n}(y)$are defined by Equations (80) and (82) respectively.

Remark 5.2

Since for $B(t)=\exp (t)$ the 2VBBGP ${}_{F}P_{n}(x,y)$ reduce to the Sheffer general polynomials ${}_{S}P_{n}(x,y)$, it follows that Sheffer general polynomials ${}_{S}P_{n}(x,y)$ satisfy the recursion relation identical to (79) with Equations (80), (81), and (82) holding.

Remark 5.3

Since for $C(t)=t$ and $B(t)=\exp (t)$ the 2VBBGP ${}_{F}P_{n}(x,y)$ reduce to the Appell general polynomials ${}_{L}P_{n}(x,y)$, from Equation (81) it follows that $\xi _{k}=0$. Thus Sheffer general polynomials ${}_{S}P_{n}(x,y)$ satisfy the recursion relation identical to (90) with Equations (80) and (82) holding.

Finally, to give an application of the result given in Theorem 5.1, we consider the following example.

Example 5.1

Since for $\varPhi (y,t)=\frac{1}{1-yt}$ the 2-variable general polynomials $P_{n}(x,y)$ reduce to 2-variable truncated exponential polynomials of order 1 $e_{n}(x,y)$ (Table 1(III)) and for $A(t)=\frac{1}{1-t}$, $B(xt)=\exp (xt)$, and $C(t)=\frac{-t}{1-t}$ the Boas–Buck polynomials reduce to Laguerre polynomials [23], putting these values in Equation (16), the 2VBBGP ${}_{F}P_{n}(x,y)$ is reduced to the Laguerre-truncated exponential polynomials (LTEP) denoted by ${}_{L}e_{n}(x,y)$ and is given by

$$ \frac{1}{(1-t)(1-yt)}\exp \biggl( \frac{-xt}{1-t} \biggr) =\sum_{n=0}^{ \infty } \,{}_{L}e_{n}(x,y) \frac{t^{n}}{n!}. $$

(91)

From the expressions of $A(t)$, $C(t)$, and $\varPhi (y,t)$, we find

$$\begin{aligned}& t\frac{A^{\prime }(t)}{A(t)}=\sum_{n=0}^{\infty } t^{n+1}, \end{aligned}$$

(92)

$$\begin{aligned}& t\frac{C^{\prime }(t)}{C(t)}=1+\sum_{n=0}^{\infty }t^{n+1}, \end{aligned}$$

(93)

and

$$ t\frac{\varPhi ^{\prime }(y,t)}{\varPhi (y,t)}=\sum_{n=0}^{\infty }y^{n}t^{n+1}. $$

(94)

On comparing Equations (92)–(94) with Equations (81)–(83), we find

$$ \alpha _{k}=\xi _{k}=(k+1)! $$

(95)

and

$$ \mu _{k}=y^{k+1}(k+1)!. $$

(96)

Using the expressions from Equations (95) and (96) in Equation (79), we get the following recurrence relation for LTEP ${}_{L}e_{n}(x,y)$:

$$\begin{aligned}& n \,{}_{L}e_{n}(x,y)-x \partial _{x}\,{}_{L}e_{n}(x,y) \\& \quad =\sum_{k=0}^{n-1}\frac{n!}{(n-k-1)!} \bigl[\bigl(y^{k}+1\bigr)\,{}_{L}e_{n-1-k}(x,y)+x \partial _{x}\,{}_{L}e_{n-1-k}(x,y) \bigr]. \end{aligned}$$

(97)

Similarly, a recurrence relation of other members belonging to this family can also be obtained.

Appendix

In the previous section, the recursion relation of 2VBBGP ${}_{F}P_{n}(x,y)$ has been obtained. In this section, we discuss the graphical and computational aspects related to these polynomials. The software “Mathematica” is used to show the behavior of LTEP ${}_{L}e_{n}(x,y)$ (which is a member of 2VBBGP ${}_{F}P_{n}(x,y)$) by means of the graph, 3D surface plot, and plotting of zeros. The LTEP ${}_{L}e_{n}(x,y)$ are defined by the generating function (91), and first few LTEP ${}_{L}e_{n}(x,y)$ are as follows:

$$ \begin{aligned} & {}_{L}e_{0}(x,y)=1, \\ & {}_{L}e_{1}(x,y)=1 - x + y, \\ & {}_{L}e_{2}(x,y)= 2 - 4 x + x^{2} + 2 y - 2 x y + 2 y^{2}, \\ & {}_{L}e_{3}(x,y)=6 - 18 x + 9 x^{2} - x^{3} + 6 y - 12 x y + 3 x^{2} y + 6 y^{2} - 6 x y^{2} + 6 y^{3}, \\ & {}_{L}e_{4}(x,y)=24 - 96 x + 72 x^{2} - 16 x^{3} + x^{4} + 24 y - 72 x y + 36 x^{2} y - 4 x^{3} y + 24 y^{2} \\ &\hphantom{{}_{L}e_{4}(x,y)={}}{} - 48 x y^{2} + 12 x^{2} y^{2} + 24 y^{3} - 24 x y^{3} + 24 y^{4}. \end{aligned}$$

The shape of LTEP ${}_{L}e_{n}(x,y)$ for $y=5$ is displayed. In Fig. 1 (left) and Fig. 1 (right), graphs for the even values (2n; $n=0,1,2,\ldots ,6$) and odd values ($2n+1$; $n=0,1,2,\ldots ,6$) are shown respectively.

Figure 1

Curve of LTEP ${}_{L}e_{n}(x,y)$

The 3D surface plots are more informative and better for analysis. The predictor variables are displayed on the x and y axes, while the response variable z is represented by a smooth surface (3D surface plot) or a grid. It helps to visualize the response surface and hence provide a more clear concept. The surface plot of LTEP ${}_{L}e_{n}(x,y)$ for $n=20$ and $n=21$ is displayed in Fig. 2.

Figure 2

Surface plot of ${}_{L}e_{20}(x,y)$ and ${}_{L}e_{21}(x,y)$

Numerical results for number of real and complex zeros of the LTEP ${}_{L}e_{n}(x,y)$ for $y=5$ are listed in Table 9.

Table 9 Numbers of real and complex zeros of ${}_{L}e_{n}(x,y)$

Approximate solution satisfying the LTEP ${}_{L}e_{n}(x,y)$ for $y=5$ is given in Table 10.

Table 10 Approximate solutions of ${}_{L}e_{n}(x,y)$

Next, we draw the graphs showing shapes with scattered real zeros of LTEP ${}_{L}e_{n}(x,y)$. In Fig. 3 (left) and Fig. 3 (right), graphs for the even value $n=20$ and odd value $n=21$ along with their real zeros are shown respectively for $y=5$.

Figure 3

Graph of ${}_{L}e_{20}(x,y)$ and ${}_{L}e_{21}(x,y)$ along with their real zeros

Using computers it has been checked for several values of n that, for $b \in \mathbb{R}$ and $x \in \mathbb{C}$, LTEP ${}_{L}e_{n}(x,b)$ has $\operatorname{Im}(x)=0$ reflection symmetry. However, LTEP ${}_{L}e_{n}(x,b)$ does not have $\operatorname{Re}(x)= a$ reflection symmetry (see Fig. 4). But it still remains unknown whether this is true or not for all values of n. In Fig. 4 (left) and Fig. 4 (right), zeros for the even value $n=20$ and odd value $n=21$ are shown respectively for $y=5$.

Figure 4

Zeros of LTEP ${}_{L}e_{n}(x,b)$ have $\operatorname{Im}(x)=0$ reflection symmetry

By using numerical investigation and computer experiments, we find the real and complex zeros and observe the phenomenon of distribution of the zeros. Real zeros of the LTEP ${}_{L}e_{n}(x,y)$ for $y=5$, $x \in \mathbb{R}$, and $1\leq n \leq 20$ are plotted in Fig. 5.

Figure 5

Real zeros of ${}_{L}e_{n}(x,y)$

Next, stacks of zeros of LTEP ${}_{L}e_{n}(x,y)=0$ for $y=5$ and $1\leq n \leq 20$ form a 3-D structure and are presented in Fig. 6.

Figure 6

Stacks of zeros of LTEP ${}_{L}e_{n}(x,y)=0$

We observed the remarkable regular structure of zeros of LTEP ${}_{L}e_{n}(x,y)=0$. Similar numerical computations give an unrestricted capability to create visual mathematical investigations of the behavior of several other polynomials belonging to 2VBBGP ${}_{F}P_{n}(x,y)$.