Convergence of neutral type SICNNs involving proportional delays and D operators

Abstract

In the present study, by employing differential inequality theory, some novel assertions are gained to validate the global exponential convergence on neutral type shunting inhibitory cellular neural networks involving proportional delays and D operators. Moreover, numerical simulations are provided to support the effectiveness of the analytical results.

1 Introduction

The well-known shunting inhibitory cellular neural networks (SICNNs), first proposed by Bouzerdoum and Pinter [1], have been extensively studied both in theory and applications [2–7]. In particular, qualitative and stability analysis for SICNNs with neutral type delays plays an important role in the design and applications of neural networks [8–11]. Usually, all neutral type SICNNs models can be converted into non-operator-based neutral functional differential equations (NFDEs) [8–10] and D-operator-based NFDEs [11], respectively.

In the past two decades, proportional delays occurring in nonlinear dynamics have attracted considerable attention because of their potential applications in various aspects such as web quality of service routing decision, collection of current of electric locomotive, nonlinear dynamical behavior, electrodynamics and principle of probability (see [12–15]). However, so far, there is existing few articles on the global exponential convergence of neutral type SICNNs involving proportional delays and D operators [16].

Inspired by the above viewpoint, in this article, our goal is to study the global exponential convergence for the following neutral type SICNNs involving proportional delays and D operators:

$$\begin{aligned}& \bigl[x _{ij} (t)-p_{ij}(t)x_{ij}( r _{ij}t)\bigr]' \\& \quad = -a_{ij}(t)x_{ij}(t)-\sum _{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)f\bigl(x_{kl}(q_{kl} t )\bigr)x_{ij}(t) +L_{ij}(t),\quad t\geq1, \end{aligned}$$

(1.1)

where $ij\in J=\{11, 12, \ldots, 1n, \ldots, m1, m2, \ldots, mn \}$, mn corresponds to the number of units in a neural network, $C_{ij}$ is the cell at the position $(i, j)$ of the lattice, $N_{r} (i, j) = \{C_{kl}: \max(| k - i |, | l - j |)\le r, 1 \le k \le m, 1 \le l \le n \}$ is the r neighborhood of $C_{ij}$, proportional delay factors $q _{kl}$ and $r_{ij}$ satisfy the conditions that $0 < q _{kl}, r_{ij} < 1$. Further information on the activation functions and coefficient parameters is available from [9, 11].

Throughout the rest of this article, the following concepts and notations will be adopted. For any $x =\{ x_{ij} \} =(x_{ij} )_{1\times mn}\in \mathbb{R}^{m n}$,

$$\begin{aligned}& \vert x \vert =\bigl\{ \vert x_{ij} \vert \bigr\} , \qquad \bigl\Vert x(t) \bigr\Vert =\max_{ij\in J} \bigl\vert x_{ij}(t) \bigr\vert , \\& \rho_{ij} =\min\{r_{ij}, q_{ ij} \},\qquad r= \frac{1}{\max_{ij \in J}\max\{ q_{ij}, r _{ij}\}}, \\& W^{+}=\sup_{t\in\mathbb{R}} \bigl\vert W(t) \bigr\vert , \qquad W^{-}=\inf_{t\in\mathbb{R}} \bigl\vert W(t) \bigr\vert . \end{aligned}$$

The initial condition involved in systems (1.1) can be described as follows:

$$ x_{ij}(s)=\varphi_{ij}(s),\quad s\in[\rho_{ij}, 1], {\varphi}_{ij }\in C\bigl([\rho_{ij}, 1], \mathbb{R}\bigr) , ij\in J. $$

(1.2)

Furthermore, it is assumed that $a_{ij}, p_{ij}, L_{ij}, C_{ij}^{kl} \in BC( [ \rho_{ij}, +\infty),\mathbb{R} )$, where $BC([ \rho_{ij}, +\infty), \mathbb{R} )$ designates the set of bounded and continuous functions, and $ij \in J$.

In addition, for $ij \in J$, the following hypotheses will be imposed:

(S₀):

There exist $\tilde{a}_{ij} \in BC(\mathbb{R}, (0, +\infty))$ and $K_{ij}>0$ satisfying

$$e ^{ -\int_{s}^{t}a_{ij}(u)\,du}\leq K_{ij} e ^{ -\int_{s}^{t}\tilde{a}_{ij}(u)\,du} \quad \forall t,s\in \mathbb{R} , t-s\geq0. $$

(S₁):

$f\in C[\mathbb{R}, \mathbb{R}]$, $\sup_{u\in\mathbb {R}}|f(u)|=M^{f}\geq0$.

(S₂):

There are constants $H_{ij}, \lambda_{0} \in(0, +\infty)$ obeying

$$H_{ij}=\sup_{ s \geq\rho_{ij}} \bigl\vert p_{ij} (s) \bigr\vert e^{\lambda_{0} (1- r_{ij}) s}< 1, \qquad L_{ij }(t)=O\bigl(e^{-\lambda_{0} t} \bigr)\quad \text{as } t\rightarrow+\infty, $$

and

$$ \sup_{t\geq1} \biggl\{ -\tilde{a}_{ij}(t)+K_{ij} \biggl[\frac{ e^{ \lambda_{0} (1- r_{ij}) t } }{1- H_{ij} } \bigl\vert a_{ij} (t)p_{ij} (t) \bigr\vert + \sum_{C_{kl}\in N_{r}(i,j)} \bigl\vert C_{ij}^{kl}(t) \bigr\vert M^{f}\frac{1}{1- H_{ij} } \biggr] \biggr\} < 0 . $$

2 Global existence and convergence of solutions

In this section, we will validate the global existence and convergence of every solution for SICNNs (1.1) with initial condition (1.2).

Lemma 2.1

If (S₀), (S₁) and (S₂) are obeyed, then every solution $x (t )$ of (1.1)–(1.2) exists and is unique on $[1, +\infty)$.

Proof

For $ij\in J$ and $t\in[1, r]$, let

$$y _{ij} (t)=x _{ij} (t)-p_{ij}(t)x_{ij}( r _{ij} t ),\qquad \beta _{ij}(t)=p_{ij}(t) \varphi_{ij}( r _{ij} t ) $$

and

$$A_{ij}(t)=a_{ij}(t) +\sum_{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)f \bigl(\varphi_{kl}(q_{kl} t )\bigr),\qquad B_{ij}(t)=-A_{ij}(t)p_{ij}(t) \varphi_{ij}( r _{ij} t ) +L_{ij}(t). $$

Then

$$\begin{aligned} y _{ij} '(t) = &\bigl[x _{ij} (t)-p_{ij}(t)x_{ij}( r _{ij} t ) \bigr]' \\ =& -a_{ij}(t)x_{ij}(t)-\sum_{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)f \bigl(x_{kl}(q_{kl} t )\bigr)x_{ij}(t) +L_{ij}(t) \\ =& -\biggl[a_{ij}(t) +\sum_{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)f \bigl(\varphi_{kl}(q_{kl} t )\bigr)\biggr]x_{ij}(t) +L_{ij}(t) \\ =& -A_{ij}(t) y_{ij}(t) +B_{ij}(t) ,\quad t\in[1, r]. \end{aligned}$$

(2.1)

From (2.1), by using a similar argument as in the proof Lemma 2.2 in [16], one can prove that $x (t )=y(t)+\{\beta_{ij}(t)\}$ exists and is unique on $[1, r], [r, r^{2}], [r^{2}, r^{3}], \ldots$ . This finishes the proofs of Lemma 2.1. This finishes the proof of Lemma 2.1. □

Theorem 2.1

Assume that all hypotheses mentioned in Sect. 1 hold. Then, there is a constant $\lambda\in(0, \lambda_{0})$ such that

$$x_{ ij }(t) =O\bigl(e^{-\lambda t}\bigr)\quad \textit{as } t \rightarrow+\infty, ij \in J, $$

where $x(t)=\{ x_{ ij }(t)\}$ is an arbitrary solution vector of the initial value problem (1.1)–(1.2).

Proof

We trivially extend $x(t)$ to $[r_{ij}\rho_{ij}, +\infty)$ by setting $x_{ij}(t) =\varphi_{ij}(t) = \varphi_{ij}(\rho_{ij})$ for $t\in [r_{ij}\rho_{ij}, \rho_{ij}]$, $ij\in J$. Let

$$X_{ij}(t)=x_{ij} (t)-p_{ij}(t)x_{ij} ( r_{ij} t ), \quad \mbox{for all } t\in[ \rho_{ij}, +\infty), ij\in J. $$

Then, $x_{ij}(t)$ and $X_{ij}(t)$ are continuous on $[ \rho_{ij}, 1]$, and

$$\begin{aligned} X_{ij}'(t) = &\bigl[x_{ij} (t)-p_{ij}(t)x_{ij} ( r_{ij} t )\bigr]' \\ =&-a_{ij}(t)X_{ij} (t )-a_{ij}(t)p_{ij}(t)x_{ij} ( r_{ij} t ) \\ &{} -\sum_{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)f \bigl(x_{kl}(q_{kl} t )\bigr)x_{ij}(t) +L_{ij}(t),\quad t\geq1, ij\in J. \end{aligned}$$

(2.2)

In view of (S₂), we can take $\lambda\in (0, \min\{ \lambda_{0}, \min_{ij\in J}\tilde{a}_{ij} ^{-}\})$ obeying

$$\begin{aligned}& \sup_{ t\geq1} \biggl\{ \lambda-\tilde{a}_{ij}(t)+K_{ij} \biggl[\frac{ e^{ \lambda(1- r_{ij}) t } }{1- H_{ij} } \bigl\vert a_{ij} (t)p_{ij} (t) \bigr\vert + \sum_{C_{kl}\in N_{r}(i,j)} \bigl\vert C_{ij}^{kl}(t) \bigr\vert M^{f}\frac{1}{1- H_{ij} } +\lambda \biggr] \biggr\} \\& \quad \leq \sup_{t\geq1} \biggl\{ \lambda-\tilde{a}_{ij}(t)+K_{ij} \biggl[\frac{ e^{ \lambda_{0} (1- r_{ij}) t } }{1- H_{ij} } \bigl\vert a_{ij} (t)p_{ij} (t) \bigr\vert \\& \qquad {}+ \sum_{C_{kl}\in N_{r}(i,j)} \bigl\vert C_{ij}^{kl}(t) \bigr\vert M^{f}\frac{1}{1- H_{ij} } +\lambda \biggr] \biggr\} < 0 ,\quad ij\in J. \end{aligned}$$

(2.3)

With no loss of generality, let

$$\|\varphi\|_{X}= \max_{ij\in J } \sup _{ t\in [\rho_{ij}, 1]} \bigl\vert \varphi_{ij} (t)-p_{ij}(t) \varphi_{ij} ( r_{ij} t ) \bigr\vert >0 . $$

For any $\varepsilon>0$, we can pick an ε-independent constant M such that

$$ M =1+\max_{ij \in J}K_{ij },\qquad \bigl\vert L_{ij }(t) \bigr\vert < \lambda M \bigl( \Vert \varphi \Vert _{X}+\varepsilon\bigr)e^{-\lambda(t-1)} \quad \mbox{for all } t\in[ 1, +\infty), ij \in J, $$

(2.4)

which leads to

$$ \bigl\Vert X(1) \bigr\Vert < \bigl( \Vert \varphi \Vert _{X}+ \varepsilon\bigr) , $$

(2.5)

and

$$ \bigl\vert X_{ij}(t) \bigr\vert < \bigl( \Vert \varphi \Vert _{X}+\varepsilon\bigr)e^{-\lambda(t-1)}< M\bigl( \Vert \varphi \Vert _{X}+\varepsilon\bigr)e^{-\lambda(t-1)} \quad \mbox{for all } t \in [ \rho_{ij}, 1], ij\in J . $$

(2.6)

Hereafter, we will validate

$$ \bigl\Vert X(t) \bigr\Vert < M\bigl( \Vert \varphi \Vert _{X}+ \varepsilon\bigr)e^{-\lambda(t-1)}\quad \mbox{for all } t > 1 . $$

(2.7)

In the contrary case, there must exist $ij \in J$ and $\theta>1$ obeying

$$ \bigl\Vert X(\theta) \bigr\Vert = \bigl\vert X_{ij}(\theta) \bigr\vert =M\bigl( \Vert \varphi \Vert _{X}+\varepsilon \bigr)e^{-\lambda (\theta-1)} $$

(2.8)

and

$$ \bigl\vert X_{kl}(t) \bigr\vert < M\bigl( \Vert \varphi \Vert _{X}+\varepsilon\bigr)e^{-\lambda(t-1)}\quad \mbox{for all } t \in[ \rho_{kl}, \theta), kl\in J. $$

(2.9)

From the fact that

$$\begin{aligned} e^{\lambda\nu} \bigl\vert x_{kl} (\nu) \bigr\vert \leq& e^{\lambda\nu } \bigl\vert x_{kl} (\nu)- p_{kl}( \nu)x_{kl} ( r_{kl} \nu) \bigr\vert +e^{\lambda\nu} \bigl\vert p_{kl}(\nu)x_{kl} ( r_{kl} \nu) \bigr\vert \\ \leq& e^{\lambda\nu} \bigl\vert X_{kl} (\nu) \bigr\vert + \bigl\vert p_{kl} (\nu) \bigr\vert e^{\lambda (1- r_{kl}) \nu} e^{\lambda r_{kl} \nu} \bigl\vert x_{kl} ( r_{kl} \nu) \bigr\vert \\ \leq& e^{\lambda \nu} \bigl\vert X_{kl} (\nu) \bigr\vert + \sup _{s \geq\rho_{kl}} \bigl\vert p_{kl} (s) \bigr\vert e^{\lambda(1- r_{kl}) s} \sup_{s\in[r_{kl} \rho_{kl }, r_{kl} t]} e^{\lambda s } \bigl\vert x_{kl} ( s ) \bigr\vert \\ \leq& e^{\lambda \nu} \bigl\vert X_{kl} (\nu) \bigr\vert + \sup _{s \geq\rho_{kl}} \bigl\vert p_{kl} (s) \bigr\vert e^{\lambda_{0} (1- r_{kl}) s} \sup_{s\in[ \rho_{kl }, t]} e^{\lambda s } \bigl\vert x_{kl} ( s ) \bigr\vert , \end{aligned}$$

(2.10)

we obtain

$$\begin{aligned} e^{\lambda t} \bigl\vert x_{kl} (t) \bigr\vert &\leq\sup _{s\in[\rho_{kl}, t]} e^{\lambda s} \bigl\vert x_{kl} (s) \bigr\vert \leq\frac{M (\|\varphi\|_{X}+\varepsilon) e^{\lambda}}{1- \sup_{s \geq\rho_{kl}}| p_{kl} (s)|e^{\lambda_{0} (1- r_{kl}) s}} \\ &= \frac{M (\|\varphi \|_{X}+\varepsilon) e^{\lambda}}{1- H_{kl}}, \end{aligned}$$

(2.11)

where $\nu\in[\rho_{kl } , t]$, $t \in[1 , \theta)$, $kl\in J$. Together with (2.4), (2.5), (2.6), (2.9) and (2.11), we conclude that

$$\begin{aligned} \bigl\vert X_{ij} (\theta) \bigr\vert =& \biggl\vert X_{ij} (1) e ^{-\int_{1}^{\theta}a_{ij}(u)\,du}+ \int_{1}^{\theta}e ^{ -\int_{t}^{\theta}a_{ij}(u)\,du}\biggl[ -a_{ij}(t)p_{ij}(t)x_{ij} ( r_{ij}t) \\ &{} -\sum_{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)f \bigl(x_{kl}(q_{kl} t )\bigr)x_{ij}(t) +L_{ij}(t)\biggr]\,dt \biggr\vert \\ \leq& \bigl\vert X_{ij} (1) \bigr\vert K_{ij}e ^{-\int_{1}^{\theta}\tilde{a}_{ij}(u)\,du}+ \int_{1}^{\theta}e ^{ -\int_{t}^{\theta}\tilde{a}_{ij}(u)\,du}K_{ij} \biggl\vert -a_{ij}(t)p_{ij}(t)x_{ij} ( r_{ij}t) \\ &{}-\sum_{C_{kl}\in N_{r}(i,j)}C_{ij}^{kl}(t)f \bigl(x_{kl}(q_{kl} t )\bigr)x_{ij}(t) +L_{ij}(t) \biggr\vert \,dt \\ \leq& \bigl( \Vert \varphi \Vert _{X}+\varepsilon \bigr)K_{ij}e ^{-\int_{1}^{\theta}\tilde{a}_{ij}(u)\,du}+ \int_{1}^{\theta}e ^{ -\int_{t}^{\theta}\tilde{a}_{ij}(u)\,du}K_{ij} \biggl[ \bigl\vert a_{ij} (t)p_{ij} (t) \bigr\vert \bigl\vert x_{ij} ( r_{ij} t ) \bigr\vert \\ &{} + \sum_{C_{kl}\in N_{r}(i,j)} \bigl\vert C_{ij}^{kl}(t) \bigr\vert M^{f} \bigl\vert x_{ij}(t) \bigr\vert + \bigl\vert L_{ij}(t) \bigr\vert \biggr] \,ds \\ \leq& \bigl( \Vert \varphi \Vert _{X}+\varepsilon \bigr)e^{-\lambda( \theta-1) }K_{ij}e ^{-\int_{1}^{\theta}[\tilde{a}_{ij}(u)-\lambda]\,du} \\ &{} + \int_{1}^{\theta}e ^{ -\int_{t}^{\theta}[\tilde{a}_{ij}(u)-\lambda]\,du} K_{ij} \biggl[\frac{ e^{ \lambda(1- r_{ij}) t } }{1- H_{ij} } \bigl\vert a_{ij} (t)p_{ij} (t) \bigr\vert \\ &{}+ \sum_{C_{kl}\in N_{r}(i,j)} \bigl\vert C_{ij}^{kl}(t) \bigr\vert M^{f}\frac{1}{1- H_{ij} } +\lambda \biggr]\,dt M\bigl( \Vert \varphi \Vert _{X}+\varepsilon\bigr)e^{-\lambda (\theta-1) } \\ \leq& \bigl( \Vert \varphi \Vert _{X}+\varepsilon \bigr)e^{-\lambda (\theta-1) }K_{ij}e ^{-\int_{1}^{\theta}[\tilde{a}_{ij}(u)-\lambda]\,du} \\ &{} + \int_{1}^{\theta}e ^{ -\int_{t}^{\theta}[\tilde{a}_{ij}(u)-\lambda]\,du} \bigl[ \tilde{a}_{ij}(t)-\lambda\bigr]\,dt M\bigl( \Vert \varphi \Vert _{X}+\varepsilon\bigr)e^{-\lambda (\theta-1) } \\ = & M\bigl( \Vert \varphi \Vert _{X}+\varepsilon \bigr)e^{-\lambda (\theta-1) }\biggl[\biggl(\frac {K_{ij}}{M}-1\biggr)e ^{-\int_{1}^{\theta}(\tilde{a}_{ij}(u)-\lambda)\,du}+ 1 \biggr] \\ < & M\bigl( \Vert \varphi \Vert _{X}+\varepsilon \bigr)e^{-\lambda (\theta-1) } . \end{aligned}$$

This is a clear contradiction of (2.8). Thus, (2.7) is true. Letting $\varepsilon\to0^{+}$ suggests

$$ \bigl\| X(t)\bigr\| \leq M\|\varphi\|_{X}e^{-\lambda(t-1)} \quad \mbox{for all } t > 1. $$

(2.12)

Then, using a similar theoretical derivation as in the proof of (2.10) and (2.11), gives us

$$e^{\lambda t} \bigl\vert x_{ij} (t) \bigr\vert \leq \sup _{s\in[\rho_{ij}, t]} e^{\lambda s} \bigl\vert x_{ij} (s) \bigr\vert \leq \frac{M \|\varphi\|_{X}e^{\lambda} }{1- H_{ij} }, $$

and

$$\bigl\vert x_{ij} (t) \bigr\vert \leq \frac{M \|\varphi\|_{X} }{1- H_{ij} }e^{-\lambda(t-1)}, \quad \forall t > 1, ij\in J. $$

This completes the proof. □

3 Simulation examples

Example 3.1

Consider the following neutral type SICNNs:

$$\begin{aligned}& \bigl[x _{ij} (t)-p_{ij}(t)x_{ij}( r _{ij}t)\bigr]' \\& \quad =-a_{ij}(t)x_{ij}(t )- \sum _{C_{kl}\in N_{1}(i,j)}C_{ij}^{kl} (t) \frac{1}{10} \arctan\bigl(x_{kl}(q_{ij} t )\bigr)x_{ij}(t) +L_{ij}(t), \end{aligned}$$

(3.1)

where $p_{ij}(t)=\frac{1}{5}e^{-t}\sin(i+j)t$, $r _{ij} = q _{ij} = \frac{1}{2}$, $i,j=1,2$,

$$\begin{array}{c}\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]=\left[\begin{array}{cc}0.8+cos100t& 1+1.1sin100t\\ 0.8+1.3cos100t& 1+1.2sin100t\end{array}\right],\hfill \\ \left[\begin{array}{cc}{C}_{11}& C_{12}\\ C_{21}& C_{22}\end{array}\right]=\left[\begin{array}{cc}0.01cos2t& 0.02cos3t\\ 0.02cos3t& 0.01cos4t\end{array}\right],\hfill \\ \left[\begin{array}{cc}{L}_{11}& L_{12}\\ L_{21}& L_{22}\end{array}\right]=\{\frac{i+j}{100}{e}^{-2|t|}sint\}.\hfill \end{array}$$

Pick

$$\begin{array}{c}\left[\begin{array}{cc}{\tilde{a}}_{11}& {\tilde{a}}_{12}\\ {\tilde{a}}_{21}& {\tilde{a}}_{22}\end{array}\right]=\left[\begin{array}{cc}0.8& 1\\ 0.8& 1\end{array}\right],K_{ij}\le e^{\frac{1}{25}},M^f=\frac{\pi }{20},\hfill \\ \sum _{C_{kl}\in N_1(i,j)}|C_{ij}^{kl}(t)|\le 0.06,{\lambda }_0=1.8,i,j=1,2,\hfill \end{array}$$

such that

$$\begin{aligned}& \sup_{t\geq1} \biggl\{ -\tilde{a}_{ij}(t)+K_{ij} \biggl[\frac{ e^{ \lambda_{0} (1- r_{ij}) t } }{1- H_{ij} } \bigl\vert a_{ij} (t)p_{ij} (t) \bigr\vert + \sum_{C_{kl}\in N_{r}(i,j)} \bigl\vert C_{ij}^{kl}(t) \bigr\vert M^{f}\frac{1}{1- H_{ij} } \biggr] \biggr\} \\& \quad < -0.2 ,\quad i,j=1,2 . \end{aligned}$$

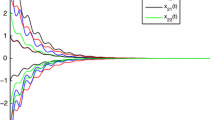
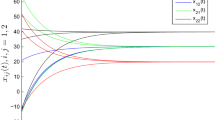
Then, it is easy to verify that (3.1) obeys (S₀), (S₁) and (S₂). Hence, by Theorem 2.1, we get that all solutions of system (3.1) converge exponentially to the zero vector with the exponential convergence rate $\lambda\approx0.02$. Furthermore, we have the following simulation results shown in Fig. 1.

Figure 1

Numerical solutions of system (3.1) with different initial values

Remark 3.1

To the best of our knowledge, this is the first time when attention is focused on the global exponential convergence for neutral type SICNNs involving proportional delays and D operators. Based on differential inequality theory, we show that all solutions of the addressed model are exponentially convergent to the zero vector under suitable hypotheses. In particular, we provide an upper bound for the exponential convergence rate. Most recently, the generalized exponential stability and pseudo almost periodicity of neutral type SICNNs have been established in [16, 17], and some other dynamical behaviors of neural networks have obtained in [18–20]. Unfortunately, the global exponential convergence for every solution of neutral type SICNNs involving proportional delays and D operators has not been investigated in [16–20]. This suggests that all results in the references [16–20] cannot be straightly applied to show the exponential convergence on every solution in system (3.1).