Abstract
The aim of the present paper is to establish some fractional  -integral inequalities on the specific time scale,
-integral inequalities on the specific time scale,  ,
,  a nonnegative integer
a nonnegative integer , where
, where  , and
, and  .
.
Similar content being viewed by others
1. Introduction
The study of fractional  -calculus in [1] serves as a bridge between the fractional
-calculus in [1] serves as a bridge between the fractional  -calculus in the literature and the fractional
-calculus in the literature and the fractional  -calculus on a time scale
-calculus on a time scale  , where
, where  , and
, and  .
.
Belarbi and Dahmani [2] gave the following integral inequality, using the Riemann-Liouville fractional integral: if  and
and  are two synchronous functions on
are two synchronous functions on  , then
, then

for all  ,
,  .
.
Moreover, the authors [2] proved a generalized form of (1.1), namely that if  and
and  are two synchronous functions on
are two synchronous functions on  , then
, then

for all  ,
,  , and
, and  .
.
Furthermore, the authors [2] pointed out that if  are
are  positive increasing functions on
positive increasing functions on  , then
, then

for any  ,
,  .
.
In this paper, we have obtained fractional  -integral inequalities, which are quantum versions of inequalities (1.1), (1.2), and (1.3), on the specific time scale
-integral inequalities, which are quantum versions of inequalities (1.1), (1.2), and (1.3), on the specific time scale  , where
, where  , and
, and  . In general, a time scale is an arbitrary nonempty closed subset of the real numbers [3].
. In general, a time scale is an arbitrary nonempty closed subset of the real numbers [3].
Many authors have studied the fractional integral inequalities and applications. For example, we refer the reader to [4–6].
To the best of our knowledge, this paper is the first one that focuses on fractional  -integral inequalities.
-integral inequalities.
2. Description of Fractional 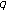 -Calculus
-Calculus
Let  and define
and define

If there is no confusion concerning  , we will denote
, we will denote  by
by  . For a function
. For a function  , the nabla
, the nabla  -derivative of
-derivative of  is
is

for all  . The
. The  -integral of
-integral of  is
is

The fundamental theorem of calculus applies to the  -derivative and
-derivative and  -integral; in particular,
-integral; in particular,

and if  is continuous at 0, then
is continuous at 0, then

Let  ,
,  denote two time scales. Let
denote two time scales. Let  be continuous let
be continuous let  be
be  -differentiable, strictly increasing, and
-differentiable, strictly increasing, and  . Then for
. Then for  ,
,

The  -factorial function is defined in the following way: if
-factorial function is defined in the following way: if  is a positive integer, then
is a positive integer, then

If  is not a positive integer, then
is not a positive integer, then

The  -derivative of the
-derivative of the  -factorial function with respect to
-factorial function with respect to  is
is

and the  -derivative of the
-derivative of the  -factorial function with respect to
-factorial function with respect to  is
is

The  -exponential function is defined as
-exponential function is defined as

Define the  -Gamma function by
-Gamma function by

Note that

The fractional  -integral is defined as
-integral is defined as

Note that

More results concerning fractional  -calculus can be found in [1, 7–9].
-calculus can be found in [1, 7–9].
3. Main Results
In this section, we will state our main results and give their proofs.
Theorem 3.1.
Let  and
and  be two synchronous functions on
be two synchronous functions on  . Then for all
. Then for all  ,
,  , we have
, we have

Proof.
Since  and
and  are synchronous functions on
are synchronous functions on  , we get
, we get

for all  ,
,  . By (3.2), we write
. By (3.2), we write

Multiplying both side of (3.3) by  , we have
, we have

Integrating both sides of (3.4) with respect to  on
on  , we obtain
, we obtain

So,

Hence, we have

Multiplying both side of (3.7) by  , we obtain
, we obtain

Integrating both side of (3.8) with respect to  on
on  , we get
, we get

Obviously,

and the proof is complete.
The following result may be seen as a generalization of Theorem 3.1.
Theorem 3.2.
Let  and
and  be as in Theorem 3.1. Then for all
be as in Theorem 3.1. Then for all  ,
,  ,
,  we have
we have

Proof.
By making similar calculations as in Theorem 3.1 we have

Integrating both side of (3.12) with respect to  on
on  , we obtain
, we obtain

Thus, (3.11) holds for all  ,
,  ,
,  , so the proof is complete.
, so the proof is complete.
Remark 3.3.
The inequalities (3.1) and (3.11) are reversed if the functions are asynchronous on  (i.e.,
(i.e.,  , for any
, for any  ).
).
Theorem 3.4.
Let  be
be  positive increasing functions on
positive increasing functions on  . Then for any
. Then for any  ,
,  we have
we have

Proof.
We prove this theorem by induction.
Clearly, for  , we have
, we have

for all  ,
,  .
.
For  , applying (3.1), we obtain
, applying (3.1), we obtain

for all  ,
,  .
.
Suppose that

Since  are positive increasing functions, then
are positive increasing functions, then  is an increasing function. Hence, we can apply Theorem 3.1 to the functions
is an increasing function. Hence, we can apply Theorem 3.1 to the functions  ,
,  . We obtain
. We obtain

Taking into account the hypothesis (3.17), we obtain

and this ends the proof.
References
Atıcı FM, Eloe PW: Fractional
 -calculus on a time scale. Journal of Nonlinear Mathematical Physics 2007,14(3):341–352.
-calculus on a time scale. Journal of Nonlinear Mathematical Physics 2007,14(3):341–352.Belarbi S, Dahmani Z: On some new fractional integral inequalities. Journal of Inequalities in Pure and Applied Mathematics 2009,10(3, article 86):-5.
Bohner M, Peterson A: Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Denton Z, Vatsala AS: Fractional integral inequalities and applications. Computers & Mathematics with Applications 2010,59(3):1087–1094.
Anastassiou GA: Multivariate fractional Ostrowski type inequalities. Computers & Mathematics with Applications 2007,54(3):434–447. 10.1016/j.camwa.2007.01.024
Anastassiou GA: Opial type inequalities involving fractional derivatives of two functions and applications. Computers & Mathematics with Applications 2004,48(10–11):1701–1731. 10.1016/j.camwa.2003.08.013
Agarwal RP: Certain fractional
 -integrals and
-integrals and  -derivatives. Proceedings of the Cambridge Philosophical Society 1969, 66: 365–370. 10.1017/S0305004100045060
-derivatives. Proceedings of the Cambridge Philosophical Society 1969, 66: 365–370. 10.1017/S0305004100045060Al-Salam WA: Some fractional
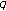 -integrals and
-integrals and 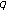 -derivatives. Proceedings of the Edinburgh Mathematical Society. Series II 1966, 15: 135–140. 10.1017/S0013091500011469
-derivatives. Proceedings of the Edinburgh Mathematical Society. Series II 1966, 15: 135–140. 10.1017/S0013091500011469Rajković PM, Marinković SD, Stanković MS: A generalization of the concept of
 -fractional integrals. Acta Mathematica Sinica (English Series) 2009,25(10):1635–1646. 10.1007/s10114-009-8253-x
-fractional integrals. Acta Mathematica Sinica (English Series) 2009,25(10):1635–1646. 10.1007/s10114-009-8253-x
Acknowledgment
The authors thank referees for suggestions which have improved the final version of this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Öğünmez, H., Özkan, U. Fractional Quantum Integral Inequalities. J Inequal Appl 2011, 787939 (2011). https://doi.org/10.1155/2011/787939
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/787939




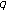 -Calculus
-Calculus -calculus on a time scale. Journal of Nonlinear Mathematical Physics 2007,14(3):341–352.
-calculus on a time scale. Journal of Nonlinear Mathematical Physics 2007,14(3):341–352. -integrals and
-integrals and 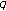 -integrals and
-integrals and 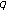 -derivatives. Proceedings of the Edinburgh Mathematical Society. Series II 1966, 15: 135–140. 10.1017/S0013091500011469
-derivatives. Proceedings of the Edinburgh Mathematical Society. Series II 1966, 15: 135–140. 10.1017/S0013091500011469 -fractional integrals. Acta Mathematica Sinica (English Series) 2009,25(10):1635–1646. 10.1007/s10114-009-8253-x
-fractional integrals. Acta Mathematica Sinica (English Series) 2009,25(10):1635–1646. 10.1007/s10114-009-8253-x