Abstract
This paper investigates the problem of exponential stabilization for a class of uncertain nonlinear systems by means of periodically intermittent control. Several sufficient conditions of exponential stabilization for this class of uncertain nonlinear systems are formulated in terms of a set of linear matrix inequalities by using quadratic Lyapunov function and inequality analysis technique. Also, the synthesis of stabilization periodically intermittent state feedback controllers is present such that the close-loop system is exponentially stable. A simulation example is given to illustrate the effectiveness of the proposed approach.
Similar content being viewed by others
1. Introduction
In recent years, significant interest in the study of stability analysis and control design of nonlinear systems has aroused [1–5]. In [4], the problem of the stabilization of affine nonlinear control systems via the center manifold approach was considered. In [5], a stabilizing output feedback model with a predictive control algorithm was proposed for linear systems with input constraints. Recently, incontinuous control techniques such as impulsive control [6] and piecewise feedback control [7] have attracted much attention. In [6], the impulsive control, which makes use of linear static measurement feedback instead of full state feedback for master-slave synchronization schemes that consist of identical chaotic Lur'e systems, was considered. Especially, the recent paper [7] has studied the output regulation problem for a class of discrete-time nonlinear systems under periodic disturbances generated from the so-called exosystems. Furthermore, by exploiting the structural information encoded in the fuzzy rules, a piecewise state feedback and a piecewise error-feedback control laws were constructed to achieve asymptotic rejecting of the unwanted disturbances and/or tracking of the desired trajectories.
Besides these control methods for nonlinear systems mentioned above, intermittent control is a special form of switching control [8]. It has been used for a variety of purposes in engineering fields such as manufacturing, transportation, air-quality control, and communication. Recently, intermittent control has been introduced to chaotic dynamical systems [9–11], in which the method of synchronizing slave-to-master trajectory using intermittent coupling was proposed. However, [9] gave little theoretical analysis of intermittent control systems but only many numerical simulations. In [10], the authors investigated the exponential stabilization problem for a class of chaotic systems with delay by means of periodically intermittent control. In [11], the quasi-synchronization problem for chaotic neural networks with parameter mismatch was formulated via periodically intermittent control. In [12], the problem of the robust stabilization for a class of uncertain linear systems with multiple time-varying delays was investigated. A memoryless state-feedback controller for the robust stabilization of the system was proposed. Based on the Lyapunov method and the linear matrix inequality (LMI) approach, two sufficient conditions for the stability were derived. In [13], a new delay-dependent stability criterion for dynamic systems with time-varying delays and nonlinear perturbations was proposed.
Motivated by the aforementioned discussion, in this paper, we investigate the problem of exponential stabilization of a class of uncertain nonlinear systems by using periodically intermittent control, which is activated in certain nonzero time intervals, and off in other time intervals. Based on Lyapunov stability theory, some exponential stability criteria for this class of uncertain nonlinear systems are given, which have been expressed in terms of linear matrix inequalities (LMIs). A numerical example is given to demonstrate the validity of the result.
The rest of this paper is organized as follows. In Section 2, the intermittent control problem is formulated and some notations and lemmas are introduced. In Section 3, the exponential stabilization problem for a class of uncertain nonlinear systems is investigated by means of periodically intermittent control, and some exponential stability criteria are established. Finally, some conclusions and remarks are drawn in Section 4.
2. Problem Formulation and Preliminaries
Consider a class of nonlinear uncertain systems described as

where  is state vector, and
is state vector, and  is the external input of system (2.1).
is the external input of system (2.1).  is a continuous nonlinear function with
is a continuous nonlinear function with  , and there exists a positive definite matrix
, and there exists a positive definite matrix  such that
such that  for
for  .
. and
and  are time-varying uncertainties, which satisfy the following conditions:
are time-varying uncertainties, which satisfy the following conditions:

where  ,
,  ,
,  are real constant matrices of appropriate dimensions and
are real constant matrices of appropriate dimensions and  is an unknown time-varying matrix with
is an unknown time-varying matrix with  .
.
The following lemmas are useful in the proof of our main results.
Lemma 2.1 (see [14]).
Let  ,
,  , and
, and  be real matrices of appropriate dimensions with
be real matrices of appropriate dimensions with  , then for any scalar
, then for any scalar  , one has the following inequality:
, one has the following inequality:

Lemma 2.2 (see [15]).
Let  ,
,  be real matrices of appropriate dimensions. Then, for any matrix
be real matrices of appropriate dimensions. Then, for any matrix  of appropriate dimension and any scalar
of appropriate dimension and any scalar  , the following inequality holds:
, the following inequality holds:

Lemma 2.3 (see [16]).
Given constant symmetric matrices  ,
,  ,
,  , and
, and  , then
, then  if and only if
if and only if

In order to stabilize the system (2.1) by means of periodically intermittent feedback control, we assume that the control imposed on the system is of the following form:

where  is the control gain matrix,
is the control gain matrix,  denotes the control period, and
denotes the control period, and  is called the control width. Our objective is to design suitable
is called the control width. Our objective is to design suitable  , and
, and  such that the system (2.1) can be stabilized.
such that the system (2.1) can be stabilized.
With control law (2.6), system (2.1) can be rewritten as

The above system is classical uncertain switched one where the switching rule only depends on time. Although there are many successful applications of intermittent control, the theoretical analysis on intermittent control system has received little attention. In this paper, we will make a contribution to this issue.
Throughout this paper, we use  ,
,  to denote the transpose and the minimum (maximum) eigenvalue of a square matrix
to denote the transpose and the minimum (maximum) eigenvalue of a square matrix  , respectively. The vector (or matrix) norm is taken to be Euclidian, denoted by
, respectively. The vector (or matrix) norm is taken to be Euclidian, denoted by  . We use
. We use  to denote a positive (negative, seminegative, and semipositive) definite matrix
to denote a positive (negative, seminegative, and semipositive) definite matrix  .
.
3. Exponential Stabilization of a Class of Uncertain Nonlinear System
This section addresses the exponential stability problem of the switched system (2.7). The main result is stated as follows.
Theorem 3.1.
The system (2.7) is exponentially stable, if there exists a positive definite matrix  , scalar constants
, scalar constants  ,
,  , such that the following LMIs hold:
, such that the following LMIs hold:


where

Moreover, the solution  satisfies the condition
satisfies the condition

Proof.
Consider the following candidate Lyupunov function

which implies that

When  , the derivative of formula (3.5) with respect to time
, the derivative of formula (3.5) with respect to time  along the trajectories of the first subsystem of system (2.7) is calculated and estimated as follows:
along the trajectories of the first subsystem of system (2.7) is calculated and estimated as follows:

Using Lemmas 2.1 and 2.2, we get

From formula (3.1) and Lemma 2.3, we have

Hence, we get

where  .
.
Thus, we have

which implies that when 

Similarly, when  , we have
, we have

From formula (3.2) and Lemma 2.3, we have

Hence, it is obtained that

where  .
.
So, we derive that when ,
,


From inequalities (3.12) and (3.17), we have the following.
When  ,
,  and
and  .
.
When  ,
,

When  ,
,

When  ,
,

When  ,
,

When  ,
,

When  , that is,
, that is,  ,
,

When  , that is,
, that is, ,
,

From inequalities (3.23) and (3.24), it follows that for any  ,
,

Hence, we get

that is,

which concludes the proof.
Remark 3.2.
In [17], the problem of an exponential stability for time-delay systems with interval time-varying delays and nonlinear perturbations was investigated. Based on the Lyapunov method, a new delay-dependent criterion for exponential stability is established in terms of LMI. However, in [17], the control is not concerned in the systems. In our paper, as  , the periodic feedback will be reduced to the general continuous feedback. In this case, formula (3.1) gives an exponential stability criterion for the system (2.1) with continuous feedback control
, the periodic feedback will be reduced to the general continuous feedback. In this case, formula (3.1) gives an exponential stability criterion for the system (2.1) with continuous feedback control  . Hence, our result have a wider area of applications.
. Hence, our result have a wider area of applications.
Corollary 3.3.
If there exist a symmetric and positive definite matrix  , scalar constants
, scalar constants  ,
,  ,
,  , such that the following LMIs hold:
, such that the following LMIs hold:


then the system (2.7) is exponentially stable, and moreover,

Proof.
Set  ,
,  , and
, and  . From (3.29) and Lemma 2.3, we get
. From (3.29) and Lemma 2.3, we get

So, formula (3.2) holds. From formulae (3.31), (3.28), and Lemma 2.3, we obtain

So, formula (3.1) holds. According to Theorem 3.1, the conclusion is obtained.
Now, we consider the following uncertain nonlinear system

where  ,
,  ,
,  is inverse.
is inverse. and
and  are time-varying uncertainties with
are time-varying uncertainties with  and satisfy
and satisfy  , in which
, in which  and
and  are real constant matrices of appropriate dimensions.
are real constant matrices of appropriate dimensions.  is a continuous nonlinear function satisfying
is a continuous nonlinear function satisfying  , and there exists a positive definite matrix
, and there exists a positive definite matrix  such that
such that  for
for  .
.
Consider the following control law:

where  . Then, the system (3.33) with formula (3.34) can be rewritten as
. Then, the system (3.33) with formula (3.34) can be rewritten as

Theorem 3.4.
If there exist a symmetric and positive definite matrix  , scalar constants
, scalar constants  ,
,  ,
,  ,
,  ,
,  , such that the following LMIs hold:
, such that the following LMIs hold:


then the system (3.35) is exponentially stable, and moreover,

Proof.
Consider the candidate Lyupunov function (3.5).
When  , the derivative of Lyupunov function (3.5) with respect to time
, the derivative of Lyupunov function (3.5) with respect to time  along the trajectories of the first subsystem of system (3.35) is calculated and estimated as follows:
along the trajectories of the first subsystem of system (3.35) is calculated and estimated as follows:

From formula (3.36) and Lemma 2.3, we have

where  .
.
Thus, we have

which implies that when  ,
,

Similarly, when  , we have
, we have

where  .
.
So, we derive that when  ,
,

Similar to the proof in Theorem 3.1, we can get

that is,

which completes the proof.
Example 3.5.
Consider the system (2.1) with

It is obvious that  .
.
For the positive numbers  ,
,  ,
,  , by solving LMIs of Corollary 3.3, we obtain
, by solving LMIs of Corollary 3.3, we obtain

Therefore, the system is robustly exponentially stabilizable with feedback control

and the solution of the system satisfies

Simulation result is shown in Figure 1 for the initial condition  ,
,  ,
,  , and
, and  , where
, where  and
and  are random constants between 0 and 1. It is seen from Figure 1 that the closed-loop system is exponentially stable.
are random constants between 0 and 1. It is seen from Figure 1 that the closed-loop system is exponentially stable.
4. Conclusions
In this paper, we deal with the exponential stabilization problem of a class of uncertain nonlinear systems by means of periodically intermittent control. Based on Lyapunov function approach, several stability criteria have been given in terms of a set of linear matrix inequalities, and stabilization periodically intermittent state feedback controllers are proposed. Finally, a numerical example is provided to show the high performance of the proposed approach.
References
Ahn CK, Han S, Kwon WH: H ∞ finite memory controls for linear discrete-time state-space models. IEEE Transactions on Circuits and Systems II 2007,54(2):97–101.
Dong Y, Mei S: Global asymptotic stabilisation of non-linear systems. International Journal of Control 2009,82(2):279–286. 10.1080/00207170802074486
Dong Y, Fan J, Mei S: Quadratic stabilization of switched nonlinear systems. Science in China. Series F 2009,52(6):999–1006. 10.1007/s11432-009-0111-z
Cheng D, Guo Y: Stabilization of nonlinear systems via the center manifold approach. Systems & Control Letters 2008,57(6):511–518. 10.1016/j.sysconle.2006.10.029
Sun D, Li Z, Shi Y, Zhang J: Output feedback model predictive control for linear systems with input constraints. Proceedings of IEEE International Conference on Control and Automation (ICCA '07), 2007 1857–1861.
Lu JG, Hill DJ: Impulsive synchronization of chaotic Lur'e systems by linear static measurement feedback: an LMI approach. IEEE Transactions on Circuits and Systems II 2007,54(8):710–714.
Chen C, Ding Z, Feng G, Guan X: Output regulation of discrete-time nonlinear systems based on T-S fuzzy model. Proceedings of the 27th Chinese Control Conference (CCC '08), 2008 746–750.
Montgomery TL, Frey JW, Norris WB: Intermittent control systems. Environmental Science and Technology 1975,9(6):528–533. 10.1021/es60104a608
Zochowski M: Intermittent dynamical control. Physica D 2000,145(3–4):181–190. 10.1016/S0167-2789(00)00112-3
Li C, Liao X, Huang T: Exponential stabilization of chaotic systems with delay by periodically intermittent control. Chaos 2007,17(1):7.
Huang J, Li C, Han Q: Quasi-synchronization of chaotic neural networks with parameter mismatch by periodically intermittent control. Proceedings of the WRI World Congress on Computer Science and Information Engineering (CSIE '09), 2009 6: 485–489.
Park JH: Robust stabilization for dynamic systems with multiple time-varying delays and nonlinear uncertainties. Journal of Optimization Theory and Applications 2001,108(1):155–174. 10.1023/A:1026470106976
Kwon OM, Park JH, Lee SM: On robust stability criterion for dynamic systems with time-varying delays and nonlinear perturbations. Applied Mathematics and Computation 2008,203(2):937–942. 10.1016/j.amc.2008.05.097
Wang YY, Xie L, de Souza CE: Robust control of a class of uncertain nonlinear systems. Systems & Control Letters 1992,19(2):139–149. 10.1016/0167-6911(92)90097-C
Cao Y-Y, Sun Y-X, Cheng C: Delay-dependent robust stabilization of uncertain systems with multiple state delays. IEEE Transactions on Automatic Control 1998,43(11):1608–1612. 10.1109/9.728880
Kwon OM, Park JH: Exponential stability of uncertain dynamic systems including state delay. Applied Mathematics Letters 2006,19(9):901–907. 10.1016/j.aml.2005.10.017
Kwon OM, Park JH: Exponential stability for time-delay systems with interval time-varying delays and nonlinear perturbations. Journal of Optimization Theory and Applications 2008,139(2):277–293. 10.1007/s10957-008-9417-z
Acknowledgment
This work is supported by the National Nature Science Foundation of China under Grant no. 50977047.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Dong, Y., Mei, S. & Liu, J. Stability Analysis and Intermittent Control Synthesis of a Class of Uncertain Nonlinear Systems. J Inequal Appl 2011, 738285 (2011). https://doi.org/10.1155/2011/738285
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/738285



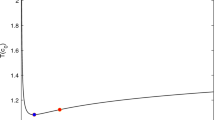

 and
and  of the closed-loop system in Example 3. 5.
of the closed-loop system in Example 3. 5.