Abstract
Numerical solutions for generalized Rosenau equation are considered and two energy conservative finite difference schemes are proposed. Existence of the solutions for the difference scheme has been shown. Stability, convergence, and priori error estimate of the scheme are proved using energy method. Numerical results demonstrate that two schemes are efficient and reliable.
Similar content being viewed by others
1. Introduction
Consider the following initial-boundary value problem for generalized Rosenau equation:

with an initial condition

and boundary conditions

where  is a integer.
is a integer.
When  , (1.1) is called as usual Rosenau equation proposed by Rosenau [1] for treating the dynamics of dense discrete systems. Since then, the Cauchy problem of the Rosenau equation was investigated by Park [2]. Many numerical schemes have been proposed, such as
, (1.1) is called as usual Rosenau equation proposed by Rosenau [1] for treating the dynamics of dense discrete systems. Since then, the Cauchy problem of the Rosenau equation was investigated by Park [2]. Many numerical schemes have been proposed, such as  -conforming finite element method by Chung and Pani [3], discontinuous Galerkin method by Choo et al. [4], orthogonal cubic spline collocation method by Manickam [5], and finite difference method by Chung [6] and Omrani et al. [7]. As for the generalized case, however, there are few studies on theoretical analysis and numerical methods.
-conforming finite element method by Chung and Pani [3], discontinuous Galerkin method by Choo et al. [4], orthogonal cubic spline collocation method by Manickam [5], and finite difference method by Chung [6] and Omrani et al. [7]. As for the generalized case, however, there are few studies on theoretical analysis and numerical methods.
It can be proved easily that the problem (1.1)–(1.3) has the following conservative law:

Hence, we propose two conservative difference schemes which simulate conservative law (1.4). The outline of the paper is as follows. In Section 2, a nonlinear difference scheme is proposed and corresponding convergence and stability of the scheme are proved. In Section 3, a linearized difference scheme is proposed and theoretical results are obtained. In Section 4, some numerical experiments are shown.
2. Nonlinear Finite Difference Scheme
Let  and
and  be the uniform step size in the spatial and temporal direction, respectively. Denote
be the uniform step size in the spatial and temporal direction, respectively. Denote  ,
,  , and
, and  . Define
. Define

and in the paper,  denotes a general positive constant which may have different values in different occurrences.
denotes a general positive constant which may have different values in different occurrences.
Since  , then the following finite difference scheme is considered:
, then the following finite difference scheme is considered:



Lemma 2.1 (see [8]).
For any two mesh functions,  , one has
, one has

Furthermore, if  , then
, then

Theorem 2.2.
Suppose  , then the scheme (2.2)–(2.4) is conservative for discrete energy, that is,
, then the scheme (2.2)–(2.4) is conservative for discrete energy, that is,

Proof.
Computing the inner product of (2.2) with  , according to boundary condition (2.4) and Lemma 2.1, we have
, according to boundary condition (2.4) and Lemma 2.1, we have

where

According to


we obtain

By the definition of  , (2.7) holds.
, (2.7) holds.
To prove the existence of solution for scheme (2.2)–(2.4), the following Browder fixed point Theorem should be introduced. For the proof, see [9].
Lemma 2.3 (Browder fixed point Theorem).
Let  be a finite dimensional inner product space. Suppose that
be a finite dimensional inner product space. Suppose that  is continuous and there exists an
is continuous and there exists an  such that
such that  for all
for all  with
with  . Then there exists
. Then there exists  such that
such that  and
and  .
.
Theorem 2.4.
There exists  satisfying the difference scheme (2.2)–(2.4).
satisfying the difference scheme (2.2)–(2.4).
Proof.
By the mathematical induction, for  , assume that
, assume that  satisfy (2.2)–(2.4). Next we prove that there exists
satisfy (2.2)–(2.4). Next we prove that there exists  satisfying (2.2)–(2.4).
satisfying (2.2)–(2.4).
Define a operator  on
on  as follows:
as follows:

Taking the inner product of (2.13) with  , we get
, we get

Obviously, for all  ,
,  with
with  . It follows from Lemma 2.3 that there exists
. It follows from Lemma 2.3 that there exists  which satisfies
which satisfies  . Let
. Let  , it can be proved that
, it can be proved that  is the solution of the scheme (2.2)–(2.4).
is the solution of the scheme (2.2)–(2.4).
Next, we discuss the convergence and stability of the scheme (2.2)–(2.4). Let  be the solution of problem (1.1)–(1.3),
be the solution of problem (1.1)–(1.3),  , then the truncation of the scheme (2.2)–(2.4) is
, then the truncation of the scheme (2.2)–(2.4) is

Using Taylor expansion, we know that  holds if
holds if  .
.
Lemma 2.5.
Suppose that  , then the solution of the initial-boundary value problem (1.1)–(1.3) satisfies
, then the solution of the initial-boundary value problem (1.1)–(1.3) satisfies

Proof.
It follows from (1.4) that

Using Hölder inequality and Schwartz inequality, we get

Hence,  . According to Sobolev inequality, we have
. According to Sobolev inequality, we have  .
.
Lemma 2.6 (Discrete Sobolev's inequality [10]).
There exist two constant  and
and  such that
such that

Lemma 2.7 (Discrete Gronwall inequality [10]).
Suppose  are nonnegative mesh functions and
are nonnegative mesh functions and  is nondecreasing. If
is nondecreasing. If  and
and

then

Theorem 2.8.
Suppose  , then the solution
, then the solution  of (2.2) satisfies
of (2.2) satisfies  , which yield
, which yield  .
.
Proof.
It follows from (2.7) that

Using Lemma 2.1 and Schwartz inequality, we get

According to Lemma 2.6, we have  .
.
Theorem 2.9.
Suppose  , then the solution
, then the solution  of the scheme (2.2)–(2.4) converges to the solution of problem (1.1)–(1.3) and the rate of convergence is
of the scheme (2.2)–(2.4) converges to the solution of problem (1.1)–(1.3) and the rate of convergence is  .
.
Proof.
Subtracting (2.15) from (2.2) and letting  , we have
, we have

Computing the inner product of (2.24) with  , and using
, and using  , we get
, we get

where

According to Lemma 2.5, Theorem 2.8, and Schwartz inequality, we have


Furthermore,

Substituting (2.27)–(2.29) into (2.25), we get

Similarly to the proof of (2.23), we have

and (2.30) can be rewritten as

Let  , then (2.32) is written as follows:
, then (2.32) is written as follows:

If  is sufficiently small which satisfies
is sufficiently small which satisfies  , then
, then

Summing up (2.34) from  to
to  , we have
, we have

Noticing

and  , we have
, we have  . Hence
. Hence

According to Lemma 2.7, we get  , that is,
, that is,

It follows from (2.31) that

By using Lemma 2.6, we have

This completes the proof of Theorem 2.9.
Similarly, the following theorem can be proved.
Theorem 2.10.
Under the conditions of Theorem 2.9, the solution of the scheme (2.2)–(2.4) is stable by  .
.
3. Linearized Finite Difference Scheme
In this section, we propose a linear-implicit finite difference scheme as follows:

Theorem 3.1.
Suppose  , then the scheme (3.1), (2.3), and (2.4) are conservative for discrete energy, that is,
, then the scheme (3.1), (2.3), and (2.4) are conservative for discrete energy, that is,

Proof.
Computing the inner product of (3.1) with  , we have
, we have

where

According to Lemma 2.1, we get


Adding (3.3) and (3.5) to (3.6), we obtain

By the definition of  , (3.2) holds.
, (3.2) holds.
Theorem 3.2.
The difference scheme (3.1) is uniquely solvable.
Proof.
we use the mathematical induction. Obviously,  is determined by (2.3) and we can choose a two-order method to compute
is determined by (2.3) and we can choose a two-order method to compute  (e.g., by scheme (2.2)). Assuming that
(e.g., by scheme (2.2)). Assuming that  are uniquely solvable, consider
are uniquely solvable, consider  in (3.1) which satisfies
in (3.1) which satisfies

Taking the inner product of (3.8) with  , we get
, we get

Notice that

It follows from (3.8) that

That is, there uniquely exists trivial solution satisfying (3.8). Hence,  in (3.1) is uniquely solvable.
in (3.1) is uniquely solvable.
To discuss the convergence and stability of the scheme (3.1), we denote the truncation of the scheme (3.1):

Using Taylor expansion, we know that  holds if
holds if  .
.
Theorem 3.3.
Suppose  , then the solution of (3.1) satisfies
, then the solution of (3.1) satisfies  , which yield
, which yield  .
.
Proof.
It follows from (3.2) that

According to (2.23), we have

that is,

If  is sufficiently small which satisfies
is sufficiently small which satisfies  , we get
, we get

which yields  . According to (2.23), we get
. According to (2.23), we get

Using Lemma 2.6, we obtain

Theorem 3.4.
Suppose  , then the solution
, then the solution  of the schemes (3.1), (2.3), and (2.4) converges to the solution of problem (1.1)–(1.3) and the rate of convergence is
of the schemes (3.1), (2.3), and (2.4) converges to the solution of problem (1.1)–(1.3) and the rate of convergence is  .
.
Proof.
Subtracting (3.12) from (3.1) and letting  , we have
, we have

Computing the inner product of (3.19) with  , we get
, we get

where

Notice that

and similarly

Furthermore, we get

Substituting (3.22)–(3.24) into (3.20), we get

Similarly to the proof of (2.31), (3.25) can be written as

Let  , then (3.26) is written as follows:
, then (3.26) is written as follows:

that is,

If  is sufficiently small which satisfies
is sufficiently small which satisfies  , then
, then

Summing up (3.29) from  to
to  , we have
, we have

Choosing a two-order method to compute  (e.g., by scheme (2.2)) and noticing
(e.g., by scheme (2.2)) and noticing

we have

According to Lemma 2.7, we get  , that is,
, that is,

According to (2.31), we get

By using Lemma 2.6, we have

This completes the proof of Theorem 3.4.
Similarly, the following theorem can be proved that.
Theorem 3.5.
Under the conditions of Theorem 3.4, the solution of the schemes (3.1), (2.3), and (2.4) are stable by  .
.
4. Numerical Experiments
Consider the generalized Rosenau equation:

with an initial condition

and boundary conditions

We construct two schemes to (4.1)–(4.3) as nonlinear scheme (2.2) and linearized scheme (3.1). Since we do not know the exact solution of (4.1)–(4.3), we consider the solution on mesh  as reference solution and obtain the error estimates on mesh
as reference solution and obtain the error estimates on mesh  , respectively, for different choices of
, respectively, for different choices of  , where we take
, where we take  . To verify the stability of schemes, we take
. To verify the stability of schemes, we take  . The maximal errors
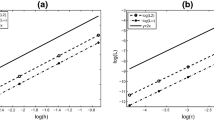
. The maximal errors  are listed on Tables 1, 2, and 3.
are listed on Tables 1, 2, and 3.
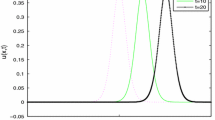
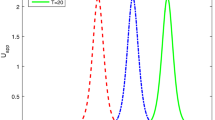
 , when
, when  and
and  .
. , when
, when  and
and  .
. , when
, when  and
and  .
.We have shown in Theorems 2.2 and 3.1 that the numerical solutions  of Scheme (2.2) and Scheme (3.1) satisfy the conservation of energy, respectively. In Figure 1, we give the values of
of Scheme (2.2) and Scheme (3.1) satisfy the conservation of energy, respectively. In Figure 1, we give the values of  for
for  with fixed
with fixed  for Scheme (2.2). In Figure 2, the values of
for Scheme (2.2). In Figure 2, the values of  for Scheme (3.1) are presented. We can see that scheme (2.2) preserves the discrete energy better than scheme (3.1).
for Scheme (3.1) are presented. We can see that scheme (2.2) preserves the discrete energy better than scheme (3.1).
From the numerical results, two finite difference schemes of this paper are efficient.
References
Rosenau P: Dynamics of dense discrete systems. Progress of Theoretical Physics 1988, 79: 1028-1042. 10.1143/PTP.79.1028
Park MA: On the rosenau equation. Matematica Aplicada e Computacional 1990, 9: 145-152.
Chung SK, Pani AK: Numerical methods for the rosenau equation. Applicable Analysis 2001,77(3-4):351-369. 10.1080/00036810108840914
Choo SM, Chung SK, Kim KI: A discontinuous galerkin method for the rosenau equation. Applied Numerical Mathematics 2008,58(6):783-799. 10.1016/j.apnum.2007.02.008
Manickam SA, Pani AK, Chung SK: A second-order splitting combined with orthogonal cubic spline collocation method for the rosenau equation. Numerical Methods for Partial Differential Equations 1998,14(6):695-716. 10.1002/(SICI)1098-2426(199811)14:6<695::AID-NUM1>3.0.CO;2-L
Chung SK: Finite difference approximate solutions for the rosenau equation. Applicable Analysis 1998,69(1-2):149-156. 10.1080/00036819808840652
Omrani K, Abidi F, Achouri T, Khiari N: A new conservative finite difference scheme for the rosenau equation. Applied Mathematics and Computation 2008,201(1-2):35-43. 10.1016/j.amc.2007.11.039
Hu B, Xu Y, Hu J: Crank-nicolson finite difference scheme for the rosenau-burgers equation. Applied Mathematics and Computation 2008,204(1):311-316. 10.1016/j.amc.2008.06.051
Browder FE: Existence and uniqueness theorems for solutions of nonlinear boundary value problems. Proceedings of Symposia in Applied Mathematics 1965, 17: 24-49.
Zhou Y: Applications of Discrete Functional Analysis to the Finite Difference Method. International Academic Publishers, Beijing, China; 1991:vi+260.
Acknowledgment
This work was supported by the Youth Research Foundation of SWUST (no. 08zx3125).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hu, J., Zheng, K. Two Conservative Difference Schemes for the Generalized Rosenau Equation. Bound Value Probl 2010, 543503 (2010). https://doi.org/10.1155/2010/543503
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/543503



 and
and  .
.
 and
and  .
.