Abstract
The presence of (Non line of Sight) NLOS propagation paths has been considered the main drawback for localization schemes to estimate the position of a (Mobile User) MU in an indoor environment. This paper presents a comprehensive wireless localization system based on (Round-Trip Time) RTT measurements in an unmodified IEEE 802.11 wireless network. It overcomes the NLOS impairment by implementing the (Prior NLOS Measurements Correction) PNMC technique. At first, the RTT measurements are performed with a novel electronic circuit avoiding the need for time synchronization between wireless nodes. At second, the distance between the MU and each reference device is estimated by using a simple linear regression function that best relates the RTT to the distance in (Line of Sight) LOS. Assuming that LOS in an indoor environment is a simplification of reality hence, the PNMC technique is applied to correct the NLOS effect. At third, assuming known the position of the reference devices, a multilateration technique is implemented to obtain the MU position. Finally, the localization system coupled with measurements demonstrates that the system outperforms the conventional time-based indoor localization schemes without using any tracking technique such as Kalman filters or Bayesian methods.
Similar content being viewed by others
1. Introduction
There is a proliferating demand for both commercial and governmental applications of wireless localization services that ascertain the position of a (mobile user) MU in an indoor environment [1]. Indoor location information can add many potential applications such as persons with special care tracking inmates monitoring, or helping policeman, fireman or soldiers to finish their missions inside buildings. However, currently signals coming from Global Navigation Satellite System (GNSS) cannot penetrate into indoor environments. Hence, alternative wireless infrastructures which offer indoor coverage have to be used. There are several existing wireless infrastructures deployed in indoor environments like ultrasonic, infrared, and artificial vision, that have been considered for indoor localization, but radiofrequency-based systems predominate today, due to their availability and low cost [2, 3]. Up to date, few wireless infrastructures that operate inside buildings are as extensively deployed and used as IEEE 802.11, a reason why this wireless technology is the best candidate for the development of an indoor localization system.
Localization methods are further classified by the measurable quantities obtained from the transmitted signals. Thus, it can be angle based as the angle of arrival (AOA) [4], range based as the measured time of arrival (TOA) [5–7] or the received signal strength (RSS) [8–10] of the MU's signal at the reference devices. This information, received on the MU, establishes a geometric relationship between the MU to be located and the reference devices. AOA measurements require antenna arrays and they are not available to inexpensive systems, while RSS measurements are widely available and provide cost-effective means of localization. However, in indoor environments the propagation phenomena cause the attenuation of the signal to poorly correlate with distance, resulting in inaccurate distance estimates. On the contrary, time-based methods are highly correlated with distance [11]. But, as TOA measurements need for time synchronization between wireless nodes, round-trip time (RTT) measurements have been used in this paper. These measurements are obtained by using the electronic circuit proposed in [12]. Once the RTT measurements have been performed between two wireless nodes, a model is used to relate the RTT to the actual distance that separates both nodes in LOSs. Previous essays [13] have used a similar electronic circuit to measure the RTT, but they use an empirical RTT-based model to estimate distances. Therefore, that model is not robust because it depends on the environment where the MU is going to be located.
Whichever the method used, a similar impairment is encountered related to indoor environments where the transmitted signal could only reach the receiver through reflected, diffracted, or scattered paths. Various NLOS (Non-Line-Of Sight) mitigation techniques have emerged to overcome this problem. They can be broadly classified in two groups, techniques which attempt to minimize the contribution of NLOS multipaths as [14] or techniques which focus on the identification of NLOS reference devices and discard them for localization [15]. However, their reliability remains questionable in an indoor environment with abundant scatterers where almost all reference devices will be in NLOS. In this paper, the PNMC (Prior NLOS Measurements Correction) technique is used to correct the NLOS effect from distance estimates [16]. This technique manages to introduce in the localization process the information that actually resides in the NLOS measurements. Once distances between the MU to be located and the reference devices in range are estimated, and assuming known the reference devices positions, different techniques could be applied to infer the MU position, like circular lateration [17] or hyperbolic lateration [18]. In this paper, an MUltilateration technique that linearizes the problem of finding the MU position is proposed to reduce its complexity and to complete the wireless localization system.
The paper is divided as follows: Section 2 describes the driver responsible to automate the localization system and Section 3 describes the localization algorithm. Section 4 analyzes the accuracy of the localization system proposed in an indoor environment. Finally, Section 5 summarizes the main achievements.
1.1. Previous Work
The main mechanism that makes RTT measurements possible in an IEEE 802.11 wireless network with a minimum elapsed time in the access point (AP) is the RTS/CTS handshake mechanism [19, 20]. In this paper, the printed circuit board (PCB) proposed in [12] is used to measure the RTT of the RTS/CTS two-frame exchange mechanism between two IEEE 802.11 wireless nodes. The way in which the PCB works is as follows: the MU enables the measuring system before sending the RTS frame and disables it after receiving the CTS frame response. Within that time the PCB extracts both transmission pulses and receiver signals from the MU wireless adapter in such a way that the RTS frame departure is used as the trigger to start the count that would be stopped by the corresponding CTS frame arrival. Despite the short lapse of time between the measuring system activation and the RTS departure or between the RTS departure and the CTS arrival, a frame coming from other wireless nodes could interfere activating or deactivating the count, respectively. As this interference could occur, a filter which rejects measurements out of the expected range has been implemented. After the RTS/CTS handshake is completed the MU saves the state of the count.
The measuring system proposed has some limitations. Firstly, as the  that governs the PCB is 44 MHz frequency, the 16-bit counter implemented on the PCB cannot measure RTTs over 1.489 ms, but this time is enough for wireless networks range. Secondly, as a frame coming from other wireless nodes could activate or deactivate the count within the short lapse of time in which the measuring system is enabled, a filter that rejects these undesirable measurements is implemented. Filter limits have been chosen based on previous trials where there were no other wireless nodes interfering. Finally, according to [12] the elapsed time in the AP, between receiving an RTS frame and sending the corresponding CTS frame, can be assumed to be constant when there are no other processes competing for the AP resources. Obviously, although the RTS frame has the highest priority in [19], it could be concurrent RTS frames coming from other MUs at the same AP increasing the load of the AP. In that case, if there are not enough APs in range to apply the localization algorithm, the wireless localization system delay increases, but the accuracy is not degraded thanks to the previous filter that rejects the RTT measurements that are out of the expected range.
that governs the PCB is 44 MHz frequency, the 16-bit counter implemented on the PCB cannot measure RTTs over 1.489 ms, but this time is enough for wireless networks range. Secondly, as a frame coming from other wireless nodes could activate or deactivate the count within the short lapse of time in which the measuring system is enabled, a filter that rejects these undesirable measurements is implemented. Filter limits have been chosen based on previous trials where there were no other wireless nodes interfering. Finally, according to [12] the elapsed time in the AP, between receiving an RTS frame and sending the corresponding CTS frame, can be assumed to be constant when there are no other processes competing for the AP resources. Obviously, although the RTS frame has the highest priority in [19], it could be concurrent RTS frames coming from other MUs at the same AP increasing the load of the AP. In that case, if there are not enough APs in range to apply the localization algorithm, the wireless localization system delay increases, but the accuracy is not degraded thanks to the previous filter that rejects the RTT measurements that are out of the expected range.
2. Localization System
The first two objectives of the wireless localization system proposed in this paper are to be integrated in a commercial IEEE 802.11 wireless adapter and to be autonomous. On one hand, the PCB proposed in [12] is used to measure the RTT between two wireless nodes. On the other hand, a driver that controls that PCB is programmed to automate the process of obtaining the RTT measurements. To obtain the MU position, the driver interacts with a novel wireless localization algorithm according to the flowchart shown in Figure 1. Therefore, a complete wireless localization system to be deployed in an unmodified IEEE 802.11 wireless network is proposed.
In this paper, it is assumed that the PCB and the localization algorithm are performed in the MU side, although other combinations could be possible. The way in which the localization system obtains the MU position is by the localization algorithm that will be described in Section 3. The only input arguments needed by the localization algorithm are as follows: the APs positions that play the role of reference devices and whose positions are assumed to be known, and the RTT measurements that characterize the distance between the MU and each AP in range. Following the flowchart shown in Figure 1, the RTT measurements are obtained automatically by the PCB described in [12] thanks to the driver that works as follows.
( ) The MU wireless adapter scans the environment looking for beacon probes coming from the APs, which are commonly sent by each AP every 100 ms [19]. The power level, based on the RSS indicator (RSSI), with its corresponding MAC source address are stored when the beacon reaches the MU wireless adapter. If the MU receives beacon probes coming from no more than two APs, the MU continues scanning the environment. Once more than two APs are in range, the following action is repeated for each AP.
) The MU wireless adapter scans the environment looking for beacon probes coming from the APs, which are commonly sent by each AP every 100 ms [19]. The power level, based on the RSS indicator (RSSI), with its corresponding MAC source address are stored when the beacon reaches the MU wireless adapter. If the MU receives beacon probes coming from no more than two APs, the MU continues scanning the environment. Once more than two APs are in range, the following action is repeated for each AP.
( ) The MU wireless adapter communicates to the AP through the MAC address sending to it
) The MU wireless adapter communicates to the AP through the MAC address sending to it  RTS frames. After receiving the corresponding CTS response frames, the corresponding RTTs are stored from each RTS/CTS frame exchange. Next, regarding the RTT estimator to be used, the Fisher information is computed from the RTT measurements to calculate the minimum number of RTS/CTS frames exchange (parameter
RTS frames. After receiving the corresponding CTS response frames, the corresponding RTTs are stored from each RTS/CTS frame exchange. Next, regarding the RTT estimator to be used, the Fisher information is computed from the RTT measurements to calculate the minimum number of RTS/CTS frames exchange (parameter  in Figure 1) that are needed for a given confidence level and sample error. By this way, the localization system minimizes the number of RTS/CTS frames exchange and hence the use of the IEEE 802.11 channel which could slow down the packet delivery on the wireless network. In Appendix B, a detailed information is given about
in Figure 1) that are needed for a given confidence level and sample error. By this way, the localization system minimizes the number of RTS/CTS frames exchange and hence the use of the IEEE 802.11 channel which could slow down the packet delivery on the wireless network. In Appendix B, a detailed information is given about  computing. Therefore,
computing. Therefore,
(i)if the number of RTT measurements is lower than the computed parameter  , the MU adapter sends another
, the MU adapter sends another  RTS frames,
RTS frames,
(ii)if not, the distance between the MU and the corresponding AP is characterized by the RTT measurements carried out until that moment,
( ) once this process has been repeated for each AP in range, and if the number of APs in range is no less than three, the RTT measurements stored are ready to be used by the localization algorithm to infer the MU position.
) once this process has been repeated for each AP in range, and if the number of APs in range is no less than three, the RTT measurements stored are ready to be used by the localization algorithm to infer the MU position.
3. Localization Algorithm
After having automated the wireless localization system, its core—the localization algorithm—has to be explained. As shown in Figure 1, the localization algorithm takes as input arguments the RTT measurements carried out between the MU and each AP in range, and the position of these APs that are assumed to be previously known. As a result, the output of the localization algorithm is an estimation of the MU position. Figure 2 shows the flowchart that explains the process followed by the novel localization algorithm to estimate the MU position. Firstly, a location estimator is obtained from the RTT measurements. That value will be used in a model that characterizes the distance between the MU and the corresponding AP. As the transmitted signal could only reach the receiver through a path different from the direct one, the PNMC technique is used to correct the positive bias that introduces the NLOS error. Once the effect of NLOS error is corrected, the model that relates the actual distance to the RTT estimator in LOS is used. Finally, when the distance from the MU to more than two APs is estimated and assuming known the positions of these APs, an MUltilateration method that linearizes the problem of finding the MU position is implemented.
3.1. Statistical Estimators and Robust Linear Regression in LOS
According to [21], the range resolution is determined by the bandwidth of the transmitted signal when RTT measurements are used. Furthermore, when using a 44 MHz clock as input of the measuring system to quantify the RTT measurements, the maximum resolution achievable, if only one sample is taken, is about 6.8 m. Moreover, the RTT measurements have a random behavior due to the error introduced by the standard noise from electronic devices, that is always present. To overcome these limitations several RTT measurements have to be performed at each distance and a representative value, called the location estimator, from this group of RTT measurements has to be selected. That selection is based on the model that relates the location estimator to the distance that separates the MU and the AP in LOS.
The location of a random variable distribution can usually be presented by a single number, the location estimator. In [22], several location estimators of a random variable are analyzed. The mean, median, mode and the scale parameter of the Weibull distribution (scale-W) are examples of the location of a random variable. They have been analyzed and compared as location estimators of the RTT measurements in terms of the coefficient of determination,  . This coefficient measures how much of the original uncertainty in the RTT measurements is explained by the model [23]. In this paper, a simple linear regression function is assumed to be the model that relates the actual distance between the two nodes involved in RTT measurements to the location estimators in LOS. Analytically,
. This coefficient measures how much of the original uncertainty in the RTT measurements is explained by the model [23]. In this paper, a simple linear regression function is assumed to be the model that relates the actual distance between the two nodes involved in RTT measurements to the location estimators in LOS. Analytically,

where,  and
and  are the estimated and the actual distance between the MU and the AP in LOS, respectively,
are the estimated and the actual distance between the MU and the AP in LOS, respectively,  is the location estimator of RTT measurements,
is the location estimator of RTT measurements,  and
and  are the intercept and slope of the simple linear regression function, respectively, and
are the intercept and slope of the simple linear regression function, respectively, and  is the error introduced by
is the error introduced by  . The error term
. The error term  has been modeled as a zero-mean Gaussian random variable, because the estimators used are asymptotically Gaussian and a large amount of measurements have been used, so
has been modeled as a zero-mean Gaussian random variable, because the estimators used are asymptotically Gaussian and a large amount of measurements have been used, so

In this case, as the model is a simple linear regression function,  is simply the square of the correlation coefficient,
is simply the square of the correlation coefficient,  .
.
The parameters  and
and  that characterize the simple linear regression function do not depend on the environment where the wireless localization system is going to be deployed, but on the communication system used, that is, the MU and the AP. These parameters are computed so as to give a best fit of the location estimators to the actual distance. Most commonly, the best fit is evaluated by using the least squares method, but this method is actually not robust in the sense of outlier-resistance. Hence, robust regression has been performed as it is a form of regression analysis designed to circumvent some limitations of least squares estimates for regression models [22].
that characterize the simple linear regression function do not depend on the environment where the wireless localization system is going to be deployed, but on the communication system used, that is, the MU and the AP. These parameters are computed so as to give a best fit of the location estimators to the actual distance. Most commonly, the best fit is evaluated by using the least squares method, but this method is actually not robust in the sense of outlier-resistance. Hence, robust regression has been performed as it is a form of regression analysis designed to circumvent some limitations of least squares estimates for regression models [22].
Assuming LOS between the MU and the AP without any scatter nearby and guaranteeing the first Fresnel zone clearance of the link between both nodes, three campaigns of 300 RTT measurements were conducted for several distances from 0 to 40 m. Figure 3 shows the robust linear regression function which best fits each location estimator to be analyzed. Each location estimator has been computed from each group of 50 RTT measurements at each distance. The different location estimators are analyzed and compared in terms of the coefficient of determination value,  .
.
The mode ( ) is the value that is most likely to be sampled, thereby it could be a good candidate for the location estimator, but the value that occurs the most frequently in a data set is a discrete value. Therefore, the resolution achieved,
) is the value that is most likely to be sampled, thereby it could be a good candidate for the location estimator, but the value that occurs the most frequently in a data set is a discrete value. Therefore, the resolution achieved,  , is not enough for indoor localization systems. The same resolution is achieved with the median (
, is not enough for indoor localization systems. The same resolution is achieved with the median ( ) as it is a discrete value separating the higher half of a data set. Figures 3(a) and 3(b) show that the Gaussian distributions that characterize the errors
) as it is a discrete value separating the higher half of a data set. Figures 3(a) and 3(b) show that the Gaussian distributions that characterize the errors  of the mode and the median are the widest, with
of the mode and the median are the widest, with  m being
m being  and
and  m being
m being  .
.
The mean ( ) is equivalent to the center of gravity of the distribution and it does not take discrete values, thereby the resolution is improved. Although the mean is rather sensitive in the presence of outliers, the use of a robust regression function circumvents this limitation. Figure 3(c) shows that the errors committed when using the mean as a location estimator are characterized by a Gaussian with
) is equivalent to the center of gravity of the distribution and it does not take discrete values, thereby the resolution is improved. Although the mean is rather sensitive in the presence of outliers, the use of a robust regression function circumvents this limitation. Figure 3(c) shows that the errors committed when using the mean as a location estimator are characterized by a Gaussian with  m, being
m, being  , lower than the error commit when the median. But Figure 3(d) shows that the best location estimator is the scale-W parameter (
, lower than the error commit when the median. But Figure 3(d) shows that the best location estimator is the scale-W parameter ( ) once Weibull distribution is fitted to the RTT measurements. In this case
) once Weibull distribution is fitted to the RTT measurements. In this case  is characterized by
is characterized by  m and
m and  . Therefore, the assumption of a linear function as the model that relates RTT measurements to distance is corroborated by a value of
. Therefore, the assumption of a linear function as the model that relates RTT measurements to distance is corroborated by a value of  close to the unit. This value indicates that the regression line nearly fits the
close to the unit. This value indicates that the regression line nearly fits the  perfectly.
perfectly.
Figure 4 shows the cumulative distribution function (CDF) of  . As the mode and the median take discrete values, the CDF has a step-shape with large errors. The mean has a good behavior with an error lower than 2 m on average. But the scale-W parameter with an error lower than 3 m for a cumulative probability of 80% achieves the best behavior.
. As the mode and the median take discrete values, the CDF has a step-shape with large errors. The mean has a good behavior with an error lower than 2 m on average. But the scale-W parameter with an error lower than 3 m for a cumulative probability of 80% achieves the best behavior.
There is no phenomenological explanation for choosing the scale-W parameter as location estimator of the RTT measurements set, but this parameter is another kind of a location estimator since the maximum likelihood estimator (MLE) of the scale-W parameter is the Hölder mean [24], a generalized form of the Pythagorean means, taking as parameter the shape parameter of Weibull distribution (for more detail see Appendix A).
Once scale-W parameter is found as the statistical estimator of the RTT measurements that best fits the actual distance when using a simple robust linear regression function as the model that relates the estimator to the distance, its performance is compared to an RSS-based solution to evaluate the goodness of the proposed one. The same two wireless nodes have been used in the same LOS environment. As it is well known the distance between two wireless devices causes an attenuation in the RSS values. This attenuation is known as path loss and it is modeled to be inversely proportional to the distance between both devices raised to a certain exponent. According to [8], the distance between two wireless nodes can be estimated from RSS measurements by

where  is the estimated distance between the MU and the AP,
is the estimated distance between the MU and the AP,  is the RSS measured in logarithmic units at the reference distance of
is the RSS measured in logarithmic units at the reference distance of  ,
,  is the average RSS in logarithmic units at the actual distance, and
is the average RSS in logarithmic units at the actual distance, and  is the path loss exponent. According to [20], for any distance under 20 m in LOS,
is the path loss exponent. According to [20], for any distance under 20 m in LOS,  is recommended to be 2 while
is recommended to be 2 while  for longer distances. Therefore, having taken this value for the path loss exponent and from the RSS values measured between both devices, the distance between the two wireless nodes can be estimated by using the expression (3). In Figure 4 that it can be appreciated the great accuracy obtained by the method presented (square marks), since it outperforms the RSS range based method, specially for cumulative probabilities larger than 50%.
for longer distances. Therefore, having taken this value for the path loss exponent and from the RSS values measured between both devices, the distance between the two wireless nodes can be estimated by using the expression (3). In Figure 4 that it can be appreciated the great accuracy obtained by the method presented (square marks), since it outperforms the RSS range based method, specially for cumulative probabilities larger than 50%.
3.2. NLOS Correction
The two sources of range measurement errors in localization techniques are mainly electronic errors and NLOS errors. Electronic errors are inherent to electronic devices and they are commonly modeled as a zero-mean Gaussian distribution. In the previous section, assuming LOS propagation, the effect caused by the electronic error has been minimized by choosing the best location estimator of the RTT measurements, the scale-W parameter. But the assumption of LOS condition is an oversimplification of reality in an indoor environment. Therefore, a method to correct the bias that introduces the NLOS in range measurements has to be implemented to improve the indoor wireless localization system.
The easiest method for dealing with NLOS conditions is simply to place APs at additional locations and select those from LOS, but one of the objectives of this paper is to deploy a wireless localization system in a common and unmodified wireless network. Therefore, the PNMC technique [16] is implemented to correct the NLOS errors in range measurements. The PNMC technique was created to correct the NLOS errors in open areas. Its performance has been evaluated by simulations in [16], but as it will be shown in this paper, it also works under indoor environment conditions. Based on a statistical process, the PNMC technique corrects the NLOS effect from a record of range measurements taken through a time window in a previous stage to the positioning process. This processing relies on the statistical estimate of the NLOS range measurements ratio present in the record. The ratio is used to identify the NLOS recorded range measurements. Subsequently, the NLOS range measurements are classified in segments according to the NLOS statistical distribution. Finally, the correction is carried out by subtracting the expected NLOS errors for each segment. For a detailed explanation on the PNMC technique, see [16].
Let  be the actual distance between the MU and the AP, thus
be the actual distance between the MU and the AP, thus

where  and
and  are the estimated and the actual distances between the MU and the AP, respectively. The term
are the estimated and the actual distances between the MU and the AP, respectively. The term  denotes the error. This error is the sum of two independent errors,
denotes the error. This error is the sum of two independent errors,  , where
, where  describes the electronic errors, while
describes the electronic errors, while  is the error due to the lack of direct sight between the MU and the AP. On one hand, the term
is the error due to the lack of direct sight between the MU and the AP. On one hand, the term  has been evaluated in the previous section and it was found as a zero-mean Gaussian with
has been evaluated in the previous section and it was found as a zero-mean Gaussian with  m. On the other hand, the term
m. On the other hand, the term  can follow different statistical distributions, Gaussian, Exponential, Gamma, and so forth [16]. But, regarding the distribution of
can follow different statistical distributions, Gaussian, Exponential, Gamma, and so forth [16]. But, regarding the distribution of  , it can be characterized by its mean and standard deviations. These parameters, as well as the distribution type of
, it can be characterized by its mean and standard deviations. These parameters, as well as the distribution type of  , depends on the particular environment, but it can be assumed that the NLOS propagation conditions do not change significantly in the time window that contains the record of range measurements, so the mean and standard deviation of
, depends on the particular environment, but it can be assumed that the NLOS propagation conditions do not change significantly in the time window that contains the record of range measurements, so the mean and standard deviation of  can be assumed to be constant. Moreover, the parameters that characterize
can be assumed to be constant. Moreover, the parameters that characterize  can be obtained previously to the localization process by the estimates performed in the environment where the localization system is going to be deployed. For simplicity, the Exponential distribution has been chosen for the term
can be obtained previously to the localization process by the estimates performed in the environment where the localization system is going to be deployed. For simplicity, the Exponential distribution has been chosen for the term  . Therefore,
. Therefore,

where the  parameter is fixed previously to the localization process.
parameter is fixed previously to the localization process.
In order to show the feasibility of the PNMC technique in an indoor environment, a campaign of measurements in the second floor of the Higher Technical School of Telecommunications Engineering (ETSIT) at the University of Valladolid has been carried out. Specifically, the PNMC technique is applied to the range measurements computed between an AP and an MU 14 m away who is moving 5 m straight perpendicularly to the path that joins the AP and the MU. As  , the probability density function (PDF) of the term
, the probability density function (PDF) of the term  is the convolution of the Gaussian PDF caused by the
is the convolution of the Gaussian PDF caused by the  errors and the Exponential PDF caused by the
errors and the Exponential PDF caused by the  errors. Figure 5(a) shows the histogram of the distance estimates record and the PDF of the term
errors. Figure 5(a) shows the histogram of the distance estimates record and the PDF of the term  that best fits these estimates, where the value of the parameter
that best fits these estimates, where the value of the parameter  that best fits the data is
that best fits the data is  m
m . Once the term
. Once the term  is statistically characterized, the PNMC technique can be applied. Figure 5(b) shows the result of applying the PNMC technique to the original range measurements computed in a time window equivalent to 5 m walking. In this scenario, the ratio of
is statistically characterized, the PNMC technique can be applied. Figure 5(b) shows the result of applying the PNMC technique to the original range measurements computed in a time window equivalent to 5 m walking. In this scenario, the ratio of  errors from the record of range measurements has been 52%. Subsequently, these NLOS range measurements have been corrected by subtracting the expected NLOS errors for each segment according to the Exponential distributions. The accuracy improvement of applying the PNMC technique to find the MU position in an indoor environment is shown in Section 4.
errors from the record of range measurements has been 52%. Subsequently, these NLOS range measurements have been corrected by subtracting the expected NLOS errors for each segment according to the Exponential distributions. The accuracy improvement of applying the PNMC technique to find the MU position in an indoor environment is shown in Section 4.
3.3. Multilateration
In two-dimensions, multilateration is defined as a method for determining the intersections of  circles with
circles with  . The circles are defined by their centers
. The circles are defined by their centers  , corresponding to the known positions of the APs, and the radii
, corresponding to the known positions of the APs, and the radii  , corresponding to the distance estimates between the MU and each AP. This means that to infer the position of the MU, a system of
, corresponding to the distance estimates between the MU and each AP. This means that to infer the position of the MU, a system of  quadratic equations has to be solved. As the distance estimates between the MU and each AP do not usually match the actual distances, the circles will not cut each other in a single point. Hence, the MU position
quadratic equations has to be solved. As the distance estimates between the MU and each AP do not usually match the actual distances, the circles will not cut each other in a single point. Hence, the MU position  of the localizing wireless node can be estimated by finding
of the localizing wireless node can be estimated by finding  satisfying
satisfying

Solving (6) problem requires significant complexity and is difficult to analyze. In order to simplify the resolution of the expression (6), an alternative way to find the location of the MU is defined. Instead of using the circles as the equations to determine the MU location, the radical axes will be used. The radical axis of two circles is the locus of points at which tangents drawn to both circles have the same length. The radical axis is always a straight line and it is always perpendicular to the line connecting the centers of the circles, albeit closer to the circle of the larger radius. Let

be the equations of two circles corresponding to different APs ( ). Then, the equation of the radical axis will be the result of subtracting the two involved circles' equations. Analytically,
). Then, the equation of the radical axis will be the result of subtracting the two involved circles' equations. Analytically,

If  circles cut each other in a single point then, the
circles cut each other in a single point then, the  radical axes performed among all the pairs of circles without repetition will cut each other in the same single point. Therefore, once the radical axes among all the pairs of circles are performed, the problem of solving a system of
radical axes performed among all the pairs of circles without repetition will cut each other in the same single point. Therefore, once the radical axes among all the pairs of circles are performed, the problem of solving a system of  quadratic equations is reduced to solve a system of
quadratic equations is reduced to solve a system of  linear equations. In the common case, as the
linear equations. In the common case, as the  circles do not cut each other in a single point, the linear system is solved in a least-square sense. Let
circles do not cut each other in a single point, the linear system is solved in a least-square sense. Let

be the linear equation system defined by the radical axes with

where  is a matrix of
is a matrix of  rows and 2 columns described only by the APs coordinates, while
rows and 2 columns described only by the APs coordinates, while  is a vector of
is a vector of  components represented by the distance estimates together with the AP coordinates. In the least-squared sense the solution for the expression (9) is done via
components represented by the distance estimates together with the AP coordinates. In the least-squared sense the solution for the expression (9) is done via

where  is an estimate of the actual MU position.
is an estimate of the actual MU position.
Figure 6 shows a graphical example of the method used to multilaterate. In that scenario, the MU has four APs in range whose positions are known  . After the distance between the MU and each AP is estimated through the RTT measurements,
. After the distance between the MU and each AP is estimated through the RTT measurements,  with
with  , the four circles are well defined. Then, the six radical axes are performed from all the combinations of pairs of circles,
, the four circles are well defined. Then, the six radical axes are performed from all the combinations of pairs of circles,  . The MU position,
. The MU position,  , is obtained as the result of solving the expression (11).
, is obtained as the result of solving the expression (11).
4. Results and Discussion
The second floor of the ETSIT as a real indoor environment with several offices, rooms and many people walking around has been the selected scenario to test the wireless localization system's accuracy. The IEEE 802.11 wireless network deployed in that building has been used as the one over which the MU communicates with their APs whose positions are previously known. The accuracy achieved in the estimation of the MU position is compared for different methods which do and do not mitigate the NLOS errors.
4.1. Experimental Setup
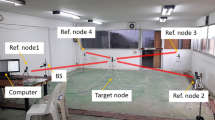
As described in Section 2, the PCB that quantifies the RTT and the localization algorithm are performed in the MU side. It includes an IEEE 802.11b wireless cardbus adapter, specifically a Cisco Aironet AIR-PCM340 with the HFA3861B baseband processor. The wireless adapter has been connected to the computer through a cardbus extender to be able to access to the HFA3861B pinout. This wireless adapter includes two on-board patch antennas with a diversity switch which toggles to and from, and stops when a significant amount of radiofrequency power is detected. The wireless network deployed in the ETSIT building consists of eight identical Linksys WRT54GL IEEE 802.11b/g APs. These APs include two rubber duck omnidirectional antennas in diversity mode that never work at the same time, since diversity circuitry switches to the one with better reception. Rubber duck antennas provide vertical polarization with 360 degrees of coverage in the horizontal plane and 75 degrees in the vertical one. The APs were configured to send a beacon frame each 100 ms at constant power on IEEE 802.11 frequency channel 1 (2.412 GHz).
Figure 7 shows the layout of the second floor of the ETSIT building where positioning tests have been carried out. The route followed by the MU describes a  rectangle walking through the middle of the corridors where each pair of continuous positions is separated 0.8 m approximately (blue dots in Figure 7). The corridors involved in the route are 2 m wide except the widest one that has a width of 4.3 m. As a consequence of the heterogeneous distribution of rooms and offices, and the people walking around, multiple reflection, diffraction or scatter points could appear and alter the signal path. Presumably, although NLOS is always present, multipath will be more noticeable when moving along the narrowest corridors.
rectangle walking through the middle of the corridors where each pair of continuous positions is separated 0.8 m approximately (blue dots in Figure 7). The corridors involved in the route are 2 m wide except the widest one that has a width of 4.3 m. As a consequence of the heterogeneous distribution of rooms and offices, and the people walking around, multiple reflection, diffraction or scatter points could appear and alter the signal path. Presumably, although NLOS is always present, multipath will be more noticeable when moving along the narrowest corridors.
According to the wireless localization system proposed in this paper, at each position groups of  RTS/CTS frames exchange have been performed before computing the boundary
RTS/CTS frames exchange have been performed before computing the boundary  . The aim of the parameter
. The aim of the parameter  is to minimize the use of the IEEE 802.11 channel which could slow down the packet delivery on the wireless network. This parameter is computed at each position according to the confidence interval (CI) explained in Appendix B. The error introduced by the term
is to minimize the use of the IEEE 802.11 channel which could slow down the packet delivery on the wireless network. This parameter is computed at each position according to the confidence interval (CI) explained in Appendix B. The error introduced by the term  is corrected by using the PNMC technique, where
is corrected by using the PNMC technique, where  is observed to be exponentially distributed with
is observed to be exponentially distributed with  m
m and a time window equivalent to 4 m walking is used. As location estimator, the scale-W parameter has been implemented to reduce the error produced by the term
and a time window equivalent to 4 m walking is used. As location estimator, the scale-W parameter has been implemented to reduce the error produced by the term  . Finally the multilateration method explained in Section 3 has been implemented to linearize the problem of estimating the MU position.
. Finally the multilateration method explained in Section 3 has been implemented to linearize the problem of estimating the MU position.
4.2. Discussion
The performance of the wireless localization algorithm is compared to other cited solutions in an indoor environment to evaluate the goodness of the methods proposed in this paper. They are as follows.
(1)An empirical range method that is also RTT-based [13]. This method consists on estimating the distance between the MU and the AP by the following empirical formula:

where  is the estimated distance by this range method,
is the estimated distance by this range method,  is the speed of the electromagnetic waves in the media,
is the speed of the electromagnetic waves in the media,  is the processing time of the AP that is calculated as the mean of the RTT measurements when
is the processing time of the AP that is calculated as the mean of the RTT measurements when  ,
,  is the measuring circuit frequency, and
is the measuring circuit frequency, and  is an empirical estimator of the RTT. Specifically,
is an empirical estimator of the RTT. Specifically,  , where
, where  and
and  are the mean and standard deviation of the RTT measurements at each distance, respectively.
are the mean and standard deviation of the RTT measurements at each distance, respectively.
(2)The RSS-based range method described by the expression (3) and assuming the paths loss exponent to be  for distances shorter then 20 m and
for distances shorter then 20 m and  for larger distances.
for larger distances.
(3)The residual weighting algorithm (RWGH) as a posteriori NLOS error mitigation technique. This technique is based on the sum of the residual squares taking the residual as the difference between the distance estimation and the range between the position estimate and the AP position. For a detailed explanation on the RWGH technique, see [14].
In Figure 7, green dots correspond to multilateration obtained by using the localization algorithm proposed in this paper. At first glance, these position estimates are highly accurate for the widest corridor. However, they tend to be slightly scattered near APs with numbers 2 and 3 where offices are smaller and corridors are narrower, in other words, where signal suffers from severe multipath. In the same figure, red dots correspond to multilateration obtained by using the empirical RTT-based range method. In order to be an empirical method, its performance depends on the environment in which the MU is going to be located. Therefore, the dynamic conditions of the ETSIT building degrades its accuracy.
In order to better compare the wireless localization algorithm proposed in this paper to other solutions, the CDF of the errors is used. This error is defined as the distance between the actual MU position and the estimated one. In Figure 8, the CDFs of the errors with five different wireless localization algorithms are shown. Five multilateration results are compared in terms of accuracy improvement to the route followed in the ETSIT building as a generic indoor environment: the empirical RTT-based and RSS-based solutions to estimate distances, the localization algorithm proposed in this paper without mitigating the NLOS errors, the localization algorithm having implemented the PNMC technique to correct NLOS errors, and the same localization algorithm having implemented the RWGH method.
From Figure 8 one can appreciate that the empirical RTT-based and RSS-based methods are not suitable for NLOS environments. On the contrary, the proposed localization algorithm without any NLOS errors mitigation technique has a good behavior for NLOS environments with an error lower than 4 m on average. This error is slightly improved after implementing the posteriori NLOS error mitigation technique RWGH. However, the implementation of the PNMC technique achieves the best result with an error lower than 5 m for a cumulative probability of 70%. It is worth pointing out that this precision has been achieved only through multilateration without any tracking technique. Obviously, the positioning accuracy can be improved by using some tracking techniques such as Kalman filters or Bayessian methods, but in this paper it has been indicated that the feasibility of using the wireless localization system proposed in indoor environments without any tracking technique help.
5. Conclusions
The achievable positioning accuracy of traditional wireless localization systems is limited when harsh radio propagation conditions like rich multipath indoor environments are present. In this paper, a novel RTT-based algorithm to locate devices in such scenarios has been proposed. The wireless localization system proposed has been developed over a hardware solution that performs RTT measurements. The effect of hardware errors has been minimized by choosing the scale-W parameter as RTT estimator. A coefficient of determination value of 0.96 achieved with this estimator in LOS justified the simple linear regression function as the model that relates distance estimates to RTT measurements in LOS. As LOS is not guaranteed in an indoor environment, the accuracy of the proposed localization algorithm has been tested in a rich multipath environment without any NLOS error mitigation technique achieving an error lower than 4 m on average. However, this error is improved after having implemented the PNMC technique to correct NLOS errors. In spite of the multipath fading conditions, experimental results have been shown that the wireless localization system proposed in this paper is highly accurate, achieving an error lower than 4 m in 80% of cases. The algorithm proposed has been compared to an empirical RTT-based and RSS-based localization algorithms and to the RWGH method for mitigating the NLOS effect, concluding that the localization system gives the best results without any tracking technique help that could improve the positioning accuracy.
References
Pahlavan K, Li X, Mäkelä J-P: Indoor geolocation science and technology. IEEE Communications Magazine 2002, 40(2):112-118. 10.1109/35.983917
Liu H, Darabi H, Banerjee P, Liu J: Survey of wireless indoor positioning techniques and systems. IEEE Transactions on Systems, Man, and Cybernetics, Part C 2007, 37(6):1067-1080.
Gu Y, Lo A, Niemegeers I: A survey of indoor positioning systems for wireless personal networks. IEEE Communications Surveys and Tutorials 2009, 11(1):13-32.
Seow CK, Tan SY: Localization of omni-directional mobile device in multipath environments. Progress in Electromagnetics Research 2008, 85: 323-348.
Cheung KW, So HC, Ma W-K, Chan YT: Least squares algorithms for time-of-arrival-based mobile location. IEEE Transactions on Signal Processing 2004, 52(4):1121-1128. 10.1109/TSP.2004.823465
Wang X, Wang Z, O'Dea B: A TOA-based location algorithm reducing the errors due to non-line-of-sight (NLOS) propagation. IEEE Transactions on Vehicular Technology 2003, 52(1):112-116. 10.1109/TVT.2002.807158
Golden SA, Bateman SS: Sensor measurements for Wi-Fi location with emphasis on time-of-arrival ranging. IEEE Transactions on Mobile Computing 2007, 6(10):1185-1198.
Mazuelas S, Bahillo A, Lorenzo RM, et al.: Robust indoor positioning provided by real-time RSSI values in unmodified WLAN networks. IEEE Journal of Selected Topics in Signal Processing 2009, 3(5):821-831.
Patwari N, Hero AO III, Perkins M, Correal NS, O'Dea RJO: Relative location estimation in wireless sensor networks. IEEE Transactions on Signal Processing 2003, 51(8):2137-2148. 10.1109/TSP.2003.814469
Bahl P, Padmanabhan VN: RADAR: an in-building RF-based user location and tracking system. Proceedings of the 19th IEEE Annual Conference on Computer Communications, March 2000 2: 775-784.
Dardari D, Conti A, Ferner U, Giorgetti A, Win MZ: Ranging with ultrawide bandwidth signals in multipath environments. Proceedings of the IEEE 2009, 97(2):404-425.
Bahillo A, Prieto J, Mazuelas S, Lorenzo RM, Blas J, Fernández P: IEEE 802.11 distance estimation based on RTS/CTS two-frame exchange mechanism. Proceedings of the IEEE Vehicular Technology Conference, April 2009 1-5.
Ciurana M, Barcelo-Arroyo F, Izquierdo F: A ranging system with IEEE 802.11 data frames. Proceedings of the IEEE Radio and Wireless Symposium (RWS '07), January 2007 133-136.
Chen P-C: A non-line-of-sight error mitigation algorithm in location estimation. Proceedings of the Wireless Communications and Networking Conference (WiCOM '99), September 1999, Chengdu, China 1: 316-320.
Cong L, Zhuang W: Nonline-of-sight error mitigation in mobile location. IEEE Transactions on Wireless Communications 2005, 4(2):560-573.
Mazuelas S, Lago FA, Blas J, et al.: Prior NLOS measurement correction for positioning in cellular wireless networks. IEEE Transactions on Vehicular Technology 2009, 58(5):2585-2591.
Küpper A: Location-Based Services: Fundamentals and Operation. John Wiley & Sons, West Sussex, UK; 2005.
Chan YT, Ho KC: A Simple and efficient estimator for hyperbolic location. IEEE Transactions on Signal Processing 1994, 42(8):1905-1915. 10.1109/78.301830
Gast MS: 802.11 Wireless Networks: The Definitive Guide. O'Reilly, Sebastopol, Calif, USA; 2002.
IEEE standard for information technology—telecommunications and information exchange between systems—local and metropolitan area networks—specific requirements—part 11: wireless medium access control (MAC) and physical layer (PHY) specifications IEEE Std 802.11-2007 (Revision of IEEE Std 802.11-1999), Junary 2007
Chen VC, Ling H: Time-Frequency Transforms for Radar Imaging and Signal Analysis. Artech House, Norwood, Mass, USA; 2002.
Olive DJ: Applied Robust Statistics. Department of Mathematics, Southern Illinois University, Carbondale, Ill, USA; 2008.
Weisberg S: Applied Linear Regression. 3rd edition. John Wiley & Sons, Hoboken, NJ, USA; 2005.
Borwein JM, Borwein PB: Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity. John Wiley & Sons, New York, NY, USA; 1986.
Acknowledgment
This research is partially supported by the Directorate General of Telecommunications of the Regional Ministry of Public Works from Castilla y León (Spain).
Author information
Authors and Affiliations
Corresponding author
Appendices
A. Maximum Likelihood Estimator of the Scale Parameter of the Weibull Distribution
The scale-W parameter is estimated by using the maximum likelihood estimator (MLE) method and assuming that the shape parameter is known.
The probability density function of a Weibull (two-parameter) random variable  is
is


where  is the shape parameter and
is the shape parameter and  is the scale-W parameter.
is the scale-W parameter.
Let  be a random sample of random variables with two-parameter Weibull distribution,
be a random sample of random variables with two-parameter Weibull distribution,  and
and  . The likelihood function is
. The likelihood function is


Therefore,


thus,


In order to find the maximum,  ; then,
; then,


Hence, the MLE of the scale-W parameter is obtained


This expression is known as the generalized mean or Hölder mean.
The Hölder mean is a generalized mean of the form,


where the parameter  is an affinely extended real number,
is an affinely extended real number,  is the number of samples and
is the number of samples and  are the samples with
are the samples with  . The Hölder mean is an abstraction of the Pythagorean means which, for example, includes minimum (
. The Hölder mean is an abstraction of the Pythagorean means which, for example, includes minimum ( ), harmonic mean (
), harmonic mean ( ), geometric mean (
), geometric mean ( ), arithmetic mean (
), arithmetic mean ( ), quadratic mean (
), quadratic mean ( ), maximum (
), maximum ( ), and the MLE of the scale-W parameter (
), and the MLE of the scale-W parameter ( ) where
) where  is the shape parameter of Weibull distribution.
is the shape parameter of Weibull distribution.
Once  is the MLE of
is the MLE of  of Weibull distribution, the Fisher information (
of Weibull distribution, the Fisher information ( ) and the Cramér-Rao lower bound (
) and the Cramér-Rao lower bound ( ) are computed.
) are computed.
The Fisher information,  :
:


where


Taking  , therefore,
, therefore,


Then,


And thus, the Cramér-Rao lower bound,


B. Confidence Interval
The  boundary is used to optimize the traffic that the location system adds to the wireless network and the time needed to obtain an accurate estimation. This boundary represents the minimum number of frames needed to be injected over the wireless network in order to get a reliable location estimator at each time.
boundary is used to optimize the traffic that the location system adds to the wireless network and the time needed to obtain an accurate estimation. This boundary represents the minimum number of frames needed to be injected over the wireless network in order to get a reliable location estimator at each time.  is computed based on the CI of the location estimator. Once the scale-W parameter has been chosen as the best location estimator of RTT measurements, the CI can be analyzed. Therefore, instead of estimating the scale-W parameter by a single value, an interval likely to include it is given. How likely the interval is to contain the scale-W parameter is determined by the confidence level
is computed based on the CI of the location estimator. Once the scale-W parameter has been chosen as the best location estimator of RTT measurements, the CI can be analyzed. Therefore, instead of estimating the scale-W parameter by a single value, an interval likely to include it is given. How likely the interval is to contain the scale-W parameter is determined by the confidence level  .
.
The Fisher information of the location estimator is used to define the CI. This method is based on the assumption that RTT measurements are independent and identically-distributed. Thus, the value  given that
given that


is determined. Where the parameter  is the scale-W parameter and
is the scale-W parameter and  is the confidence level.
is the confidence level.
If the record is large enough,  , thus
, thus


As  , then
, then  and thus,
and thus,


where  is the
is the  quantile of
quantile of  and as it is shown in Appendix A,
and as it is shown in Appendix A,  .
.
Therefore, once the CI is computed,


the sample error is defined by  . Once CI and sample error are selected, it is straightforward to calculate the minimum number of frames needed, working out
. Once CI and sample error are selected, it is straightforward to calculate the minimum number of frames needed, working out  ,
,


Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bahillo, A., Mazuelas, S., Lorenzo, R.M. et al. Accurate and Integrated Localization System for Indoor Environments Based on IEEE 802.11 Round-Trip Time Measurements. J Wireless Com Network 2010, 102095 (2010). https://doi.org/10.1155/2010/102095
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/102095







 )Median (
)Median ( )Mean (
)Mean ( )Scale-W (
)Scale-W ( )
)



