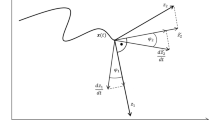
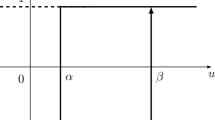
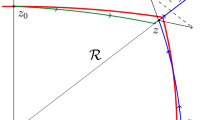
Abstract
Typically, to estimate the whole spectrum of n Lyapunov Exponents (LEs), it is necessary to integrate n perturbations and to orthogonalize them. Recently it has been shown that complexity of calculations can be reduced for smooth systems: integration of (n-1) perturbations is sufficient. In this paper authors demonstrate how this simplified approach can be adopted to non-smooth or discontinuous systems. Apart from the reduced complexity, the assets of the presented approach are simplicity and ease of implementation. The paper starts with a short review of properties of LEs and methods of their estimation for smooth and non-smooth systems. Then, the algorithm of reduced complexity for smooth systems is shortly introduced. Its adaptation to non-smooth systems is described in details. Application of the method is presented for an impact oscillator. Implementation of the novel algorithm is comprehensively explained. Results of simulations are presented and validated. It is expected that the presented method can simplify investigations of non-smooth dynamical systems and support research in this field.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
T.S. Parker, L.O. Chua,Practical Numerical Algorithms for Chaotic Systems (Springer-Verlag, Berlin, 1989)
J.L. Kaplan, J.A. Yorke, Lect. Notes Math. 730, 204 (1979)
R. Ding, J. Li, B. Li, Adv. Atmos. Sci. 34, 1027 (2017)
V.I. Oseledec, Trans. Moscow Math. Soc. 19, 197 (1968)
G. Benettin, L. Galgani, J.M. Strelcyn, Phys. Rev. A 14, 2338 (1976)
I. Shimada, T. Nagashima, Prog. Theor. Phys. 61, 1605 (1979)
G. Benettin, L. Galgani, A. Giorgilli, J.M. Strelcyn, Meccanica 15, 9 (1980)
G. Benettin, L. Galgani, A. Giorgilli, J.M. Strelcyn, Meccanica 15, 21 (1980)
A. Wolf, Chaos 16, 285 (1986)
H. Nusse, J. Yorke,Dynamics: Numerical Explorations (Springer-Verlag, New York, 1994)
A. Dabrowski, Nonlinear Dyn. 67, 283 (2012)
M. Balcerzak, A. Dabrowski, D. Pikunov, Nonlinear Dyn. 94, 3053 (2018)
A. Dabrowski, Nonlinear Dyn. 69, 1225 (2012)
A. Dabrowski, Nonlinear Dyn. 78, 1601 (2014)
M. Balcerzak, D. Pikunov, Mech. Mech. Eng. 21, 985 (2017)
W. Smiechowicz, T. Loup, P. Olejnik, Math. Comput. Appl. 24, 90 (2019)
F. Takens, Lect. Notes Math. 898, 366 (1981)
A. Wolf, J.B. Swift, H.L. Swinney, J.A. Vastano, Physica D 16, 285 (1985)
J.A. Tempkin, J.A. Yorke, SIAM J. Appl. Dyn. Syst. 6, 457 (2007)
M. Balcerzak, A. Dabrowski, A. Stefanski, J. Wojewoda, MATEC Web Conf. 148, 10003 (2018)
A. Stefanski, T. Kapitaniak, Chaos Solitons Fractals 15, 233 (2003)
L. Jin, Q.-S. Lu, E.H. Twizell, J. Sound Vib. 298, 1019 (2006)
S. De Souza, I. Caldas, Chaos Solitons Fractals 19, 171 (2004)
U. Galvanetto, Comput. Phys. Commun. 131, 1 (2000)
R.C. Hilborn,Chaos and Nonlinear Dynamics: An Introduction for Scientists and Engineers (Oxford University Press, New York, 1994)
M. Oestreich, N. Hinrichs, K. Popp, Arch. Appl. Mech. 66, 301 (1996)
D.C. Soriano, F.I. Fazanaro, R. Suyama, J.R. de Oliveira, R. Attux, M.K. Madrid, Nonlinear Dyn. 67, 413 (2012)
P. Müller, Chaos Solitons Fractals 5, 1671 (1995)
S. Zhou, X. Wang, Z. Wang, C. Zhang, Chaos 29, 033125 (2019)
A. Stefanski, Chaos Solitons Fractals 11, 2443 (2000)
A. Stefanski,Determining thresholds of complete synchronization, and application (World Scientific, Singapore, 2009)
M. Balcerzak, A. Dabrowski, B. Blazejczyk–Okolewska, A. Stefanski, Mech. Syst. Signal Process. 141, 106734 (2020)
I.N. Bronshtein, K.A. Semendyayev, G. Musiol, H. Muehlig,Handbook of Mathematics (Springer, Berlin, 2007)
K. Shin, J.K. Hammond, J. Sound Vib. 218, 389 (1998)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
The EPJ Publishers remain neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Balcerzak, M., Sagan, T., Dabrowski, A. et al. Fast and simple Lyapunov Exponents estimation in discontinuous systems. Eur. Phys. J. Spec. Top. 229, 2167–2181 (2020). https://doi.org/10.1140/epjst/e2020-900275-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1140/epjst/e2020-900275-x