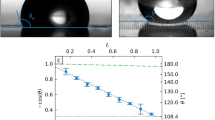
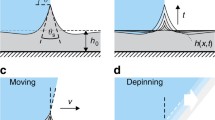
Abstract
The control of liquid droplets on solid surfaces is important in many scientific and technological applications, including microfabrication, microfluidics and heat transfer. It has been known for decades that droplets sitting on a solid surface can be moved using thermal, chemical or electrical gradients. Recent experiments have shown that gradients of substrate deformability also produce spontaneous droplet motion. This motion mechanism, which is called durotaxis, remains poorly understood. This paper proposes a model for droplet durotaxis based on a thin-film description of the fluid dynamics equation. The substrate is modeled as a Kirchhoff plate with non-constant flexural rigidity. We use high-fidelity simulations to show that the model naturally predicts droplet durotaxis without any ad hoc assumption. The model predictions for the dependence of droplet velocity on droplet size are consistent with experiments. The simplicity of the model suggests that durotaxis may be a pervasive and fundamental process at small scales and opens new possibilities to study the interaction of droplets with compliant solid surfaces.
Similar content being viewed by others
References
J. Bico, É. Reyssat, B. Roman, Annu. Rev. Fluid Mech. 50, 629 (2018)
F. Brochard, Langmuir 5, 432 (1989)
J. Bueno, Y. Bazilevs, R. Juanes, H. Gomez, Extreme Mech. Lett. 13, 10 (2017)
J. Bueno, Y. Bazilevs, R. Juanes, H. Gomez, Soft Matter 14, 1417 (2018)
J. Bueno, H. Casquero, Y. Bazilevs, H. Gomez, Meccanica 53, 1221 (2018)
M.K. Chaudhury, G.M. Whitesides, Science 256, 1539 (1992)
J. Chung, G.M. Hulbert, J. Appl. Mech. 60, 371 (1993)
N.J. Cira, A. Benusiglio, M. Prakash, Nature 519, 446 (2015)
J.A. Cottrell, T.J.R. Hughes, Y. Bazilevs, Isogeometric analysis: Toward integration of CAD and FEA, (Wiley, 2009)
M. De Volder, A.J. Hart, Angew. Chem. Int. Ed. 52, 2412 (2013)
P. Drzaic, Nat. Photonics 3, 248. (2009)
H. Gomez, V.M. Calo, Y. Bazilevs, T.J.R. Hughes, Comput. Methods Appl. Mech. Eng. 197, 4333 (2008)
H. Gomez, J. Bueno, Interaction of multiphase fluids and solid structures, in Frontiers in Computational Fluid-Structure Interaction and Flow Simulation (Springer, 2018), pp. 131–165.
H. Gomez, T.J.R. Hughes, X. Nogueira, V.M. Calo, Comput. Methods Appl. Mech. Eng. 199, 1828 (2010)
H. Gomez, K.G. van der Zee, Computational phase-field modeling, in Encyclopedia of Computational Mechanics, 2nd edn. (2018), pp. 1–35.
T.J.R. Hughes, J.A. Cottrell, Y. Bazilevs, Comput. Methods Appl. Mech. Eng. 194, 4135 (2005)
J.N. Israelachvili, Intermolecular and surface forces, (Academic press, 2011)
K.E. Jansen, C.H. Whiting, G.M. Hulbert, Comput. Methods Appl. Mech. Eng. 190, 305 (2000)
T. Liu, N. Nadermann, Z. He, S.H. Strogatz, C.-Y. Hui, A. Jagota, Langmuir 33, 4942 (2017)
R. Masurel, M. Roché, L. Limat, I. Ionescu, J. Dervaux, Phys. Rev. Lett. 122, 248004 (2019)
A. Oron, S.H. Davis, S.G. Bankoff, Rev. Mod. Phys. 69, 931 (1997)
M. Prakash, N. Gershenfeld, Science 315, 832 (2007)
O. Raccurt, F. Tardif, F.A. d’Avitaya, T. Vareine, J. Micromech. Microeng. 14, 1083 (2004)
E. Raphaël, C. R. Acad. Sci. Ser. IIB 306, 751 (1988)
Y. Saad, M.H. Schultz, SIAM J. Sci. Stat. Comput. 7, 856 (1986)
A. Sharma, Langmuir 9, 3580 (1993)
A. Sharma, Langmuir 9, 861 (1993)
M. Sokuler, G.K. Auernhammer, M. Roth, C. Liu, E. Bonacurrso, H.-J. Butt, Langmuir 26, 1544 (2009)
R.W. Style, R. Boltyanskiy, Y. Che, J.S. Wettlaufer, L.A. Wilen, E.R. Dufresne, Phys. Rev. Lett. 110, 066103 (2013)
R.W. Style, A. Jagota, C.-Y. Hui, E.R. Dufresne, Annu. Rev. Condens. Matter Phys. 8, 99 (2017)
R.W. Style, Y. Che, S.J. Park, B.M. Weon, J.H. Je, C. Hyland, G.K. German, M.P. Power, L.A. Wilen, J.S. Wettlaufer, E.R. Dufresne, Proc. Natl. Acad. Sci. 110, 12541 (2013)
T. Tanaka, M. Morigami, N. Atoda, Jpn. J. Appl. Phys. 32, 6059 (1993)
S.H. Tawfick, J. Bico, S. Barcelo, MRS Bull. 41, 108 (2016)
U. Thiele, M. Mertig, W. Pompe, Phys. Rev. Lett. 80, 2869 (1998)
C.J. Van Oss, Surface free energy contribution to cell interactions, in Biophysics of the Cell Surface (Springer, 1990), pp. 131–152
T.-S. Wong, S.H. Kang, S.K.Y. Tang, E.J. Smythe, B.D. Hatton, A. Grinthal, J. Aizenberg, Nature 477, 443 (2011)
B. Zhao, C.W. MacMinn, R. Juanes, Proc. Natl. Acad. Sci. 113, 10251 (2016)
Z. Zheng, I.M. Griffiths, H.A. Stone, J. Fluid Mech. 784, 443 (2015)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Gomez, H., Velay-Lizancos, M. Thin-film model of droplet durotaxis. Eur. Phys. J. Spec. Top. 229, 265–273 (2020). https://doi.org/10.1140/epjst/e2019-900127-x
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1140/epjst/e2019-900127-x