Abstract
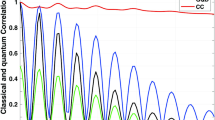
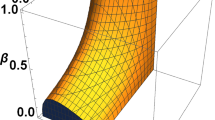
We analyse dynamics of genuinely multi-partite entanglement of N-qubit states initially prepared in the form of so called X-matrices with one qubit coupled to a Davies-type environment. We develop an analytic formula for genuinely multi-partite concurrence of the investigated states as a function of time and analyze its time evolution with an emphasis on the qualitative difference between systems affected by a pure decoherence only and those which do dissipate energy at finite temperature.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
M. Schlosshauer, Decoherence and the quantum-to-classical transition (Springer, Berlin, Heidelberg, 2007)
R. Horodecki, P. Horodecki, M. Horodecki, K. Horodecki, Rev. Mod. Phys. 81, 865 (2009)
A. Furusawa, P. van Loock, Quantum teleportation and entanglement (Wiley, Weinheim, 2011)
L. Aolita, F. de Melo, L. Davidovich, Rep. Prog. Phys. 78, 042001 (2015)
M. Michael Walter, D. Gross, J. Eisert, Multi-partite entanglement, https://doi.org/arXiv:1612.02437 (2017)
A. Acín, D. Bruß, M. Lewenstein, A. Sanpera, Phys. Rev. Lett. 87, 040401 (2001)
O. Gühne, G. Tóth, Phys. Rep. 474, 1 (2009)
M. Hofmann, T. Moroder, O. Gühne, J. Phys. A: Math. Theor. 47, 155301 (2014)
S.M. Hashemi Rafsanjani, M. Huber, C.J. Broadbent, J.H. Eberly, Phys. Rev. A 86, 062303 (2012)
E.B. Davies, Quantum Theory of Open Systems (Academic Press, London, 1976)
H. Spohn, J.L. Lebowitz, in Irreversible Thermodynamics for Quantum Systems Weakly Coupled to Thermal Reservoirs (John Wiley & Sons, Inc., 2007), p. 109
D. Kłoda, J. Dajka, Quant. Inf. Process. 14, 135 (2015)
K. Lendi, A.J. van Wonderen, J. Phys. A: Math. Theor. 40, 279 (2007)
J. Dajka, M. Mierzejewski, J. Łuczka, R. Blattmann, P. Hänggi, J. Phys. A: Math. Theor. 45, 485306 (2012)
J. Dajka, J. Łuczka, Phys. Rev. A 87, 022301 (2013)
J. Dajka, J. Łuczka, Quant. Inf. Process. 15, 2661 (2016)
M. Łobejko, J. Łuczka, J. Dajka, Phys. Rev. A 91, 042113 (2015)
J. Dajka, J. Łuczka, P. Hänggi, Quant. Inf. Process. 10, 85 (2011)
M Szela̧g, J. Dajka, E. Zipper, J. Łuczka, Acta Phys. Pol. B 39, 1177 (2008)
J. Dajka, D. Kłoda, M. Łobejko, J. Sładkowski, PLoS One 10, 1 (2015)
W. Roga, M. Fannes, K. Zyczkowski, Rep. Math. Phys. 66, 311 (2010)
R. Alicki, K. Lendi, Quantum Dynamical Semigroups and Applications, Lecture Notes in Physics (Springer, Berlin, Heidelberg, 2007)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://doi.org/creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jałowiecki, K., Dajka, J. Multi-partite entanglement in Davies environment. Eur. Phys. J. Spec. Top. 227, 2037–2041 (2019). https://doi.org/10.1140/epjst/e2019-800042-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1140/epjst/e2019-800042-9