Energy harvesting in the nonlinear two-masses piezoelastic system driven by harmonic excitations

Abstract

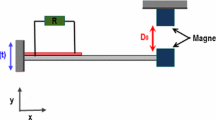
We examine the energy harvesting system consisted of two different masses (magnets) attached to piezoelastic oscillators, coupled by the electric circuit, and driven by harmonic excitations. The nonlinearity of the system is achieved by variable distance between vibrating magnetic masses and the magnets attached directly to the harvester. We also introduce the mistuning parameter which describes the disproportion of vibrating masses (their ratio). In our work we examine the dependence of output power (in terms of mean squared voltage) generated on electric load on excitation frequencies for different values of mistuning parameter and additionally for different values of system nonlinearity parameter. We compare obtained results with the dia- grams presenting relative displacements of these oscillators (in terms of standard deviation) vs. excitation frequencies. In the second part of this paper we present the phase boundary lines (phase portraits) for selected values of applied frequency to show the complicated behavior of the oscillators in the nonlinear regime when the mistuning appears.