Skip to main content
SpringerLink
Log in

Bénard-Marangoni instability in a viscoelastic ferrofluid

  • Regular Article
  • Published:
The European Physical Journal Special Topics Aims and scope Submit manuscript

Abstract

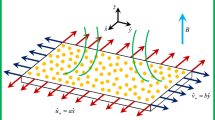
In this paper we report theoretical and numerical results on convection of a magnetic fluid in a viscoelastic carrier liquid. The viscoelastic properties are given by the Oldroyd model. We impose the lower interface to be rigid, whereas the upper one is free and is assumed to be non-deformable and flat. Also, at the upper interface the surface tension is taken to vary linearly with the temperature. Using a spectral method we calculate numerically the convective thresholds for both stationary and oscillatory bifurcations. The effect of the viscoelasticity and the Kelvin force on the instability thresholds are emphasized.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. R.E. Rosensweig, Ferrohydrodynamics (Cambridge University Press, Cambridge, 1985)

  2. S. Odenbach, Ferrofluids: Magnetically Controllable Fluids and Their Applications (Springer, Berlin, 2003)

  3. S. Odenbach (ed.), Colloidal Magnetic Fluids: Basics, Development and Application of Ferrofluids (Springer, Berlin, 2009)

  4. J.L. Neuringer, R.E. Rosensweig, Phys. Fluids 7, 1927 (1964)

    Article  MathSciNet  ADS  Google Scholar 

  5. B.A. Finlayson, J. Fluid Mech. 40, 753 (1970)

    Article  ADS  MATH  Google Scholar 

  6. A. Ryskin, H. Pleiner, Phys. Rev. E 69, 046301 (2004)

    Article  ADS  Google Scholar 

  7. P.J. Stiles, M. Kagan, J. Coll. Int. Sci. 134, 435 (1990)

    Article  Google Scholar 

  8. P.N. Kaloni, J.X. Lou, Phys. Rev. E 71, 066311 (2005)

    Article  ADS  Google Scholar 

  9. D. Laroze, J. Martinez-Mardones, J. Bragard, P. Vargas, Phys. A 371, 46 (2006)

    Article  Google Scholar 

  10. D. Laroze, J. Martinez-Mardones, L.M. Perez, Y. Rameshwar, Int. J. Bifur. Chaos 19, 2755 (2009)

    Article  MATH  Google Scholar 

  11. J. Singh, R. Bajaj, Fluid Dyn. Res. 43, 025502 (2011)

    Article  MathSciNet  ADS  Google Scholar 

  12. Sunil S. Poonam, M. Amit, Trans. Porous Med. 88, 421 (2011)

    Article  Google Scholar 

  13. D.D. Joseph, Fluid Dynamics of Viscoelastic Liquids (Springer, New York, 1990)

  14. H.M. Park, H.S. Lee, J. Non-Newtonian Fluid Mech. 66 1 (1996), and reference therein

    Article  Google Scholar 

  15. P.N. Kaloni, J.X. Lou, J. Non-Newtonian Fluid Mech. 103, 167 (2002)

    Article  MATH  Google Scholar 

  16. D. Laroze, J. Martinez-Mardones, AIP Conf. Proc. 913, 9 (2007)

    Article  ADS  Google Scholar 

  17. D. Laroze, J. Martinez-Mardones, L.M. Pérez, R.G. Rojas, J. Magn. Magn. Mater. 322, 3576 (2010)

    Article  ADS  Google Scholar 

  18. D. Laroze, L.M. Pérez, J. Bragard, E.G. Cordaro, J. Martinez-Mardones, Magnetohydrodynamics 47, 159 (2011)

    Google Scholar 

  19. L.M. Pérez, J. Bragard, D. Laroze, J. Martinez-Mardones, H. Pleiner, J. Magn. Magn. Mater. 323, 691 (2011)

    Article  ADS  Google Scholar 

  20. J. Weilepp, H.R. Brand, J. Phys. II (France) 6, 419 (1996)

    Article  Google Scholar 

  21. M. Hennenberg, B. Weyssow, S. Slavtchev, J.C. Legros, Eur. Phys. J. Appl. Phys. 16, 217 (2001)

    Article  ADS  Google Scholar 

  22. G. Lebon, A. Cloot, J. Non-Newtonian Fluid Mech. 28, 61 (1988)

    Article  MATH  Google Scholar 

  23. P. Parmentier, G. Lebon, V. Regnier, J. Non-Newtonian Fluid Mech. 89, 63 (2000), and reference therein

    Article  MATH  Google Scholar 

  24. M. Hennenberg, B. Weyssow, S. Slavtchev, V. Alexandrov, T. Desaive, J. Magn. Magn. Mater. 289, 268 (2005)

    Article  ADS  Google Scholar 

  25. M. Hennenberg, B. Weyssow, S. Slavtchev, B. Scheid, Fluid Dyn. Mat. Process. 1, 101 (2007)

    Google Scholar 

  26. M. Hennenberg, S. Slavtchev, B. Weyssow, Inter. Trans. Phenom.: Ann. N.Y. Acad. Sci. 1161, 361 (2009)

    Article  ADS  MATH  Google Scholar 

  27. C.E. Nanjundappa, I.S. Shivakumara, R. Arunkumar, J. Magn. Magn. Mater. 322, 2256 (2010)

    Article  ADS  Google Scholar 

  28. C.E. Nanjundappa, I.S. Shivakumara, R. Arunkumar, Microgravity Sci. Technol. 23, 29 (2011)

    Article  Google Scholar 

  29. S. Bohlius, H. Pleiner, H.R. Brand, Phys. Fluids 19, 094103 (2007)

    Article  ADS  Google Scholar 

  30. P. Parmentier, Etude thédorique des instabilités capillaires at gravifiques dans les fluides viscoélastiques (Ph.D. thesis), Université de Liège, 1997

  31. H. Pleiner, M. Liu, H.R. Brand, Rheologica Acta. 43, 502 (2004)

    Article  Google Scholar 

  32. P. Kolodner, J. Non-Newtonian Fluid Mech. 75, 167 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  33. T.T. Perkins, D.E. Smith, S. Chu, Science 276, 2016 (1997)

    Article  Google Scholar 

  34. S.R. Quake, H. Babcock, S. Chu, Nature 388, 151 (1997)

    Article  ADS  Google Scholar 

  35. H. Babcock, D.E. Smith, J.S. Hur, E.S.G. Shaqfeh, S. Chu, Phys. Rev. Lett. 85, 2018 (2000)

    Article  ADS  Google Scholar 

  36. D.A. Nield, J. Fluid Mech. 19, 341 (1964)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  37. L.N. Trefethen, Spectral Methods in Matlab (SIAM, Philadelphia, 2000)

  38. D. Laroze, J. Martinez-Mardones, J. Bragard, Eur. Phys. J. Special Topics 146, 291 (2007)

    Article  ADS  Google Scholar 

  39. P.C. Dauby, P. Pannentier, G. Lebon, M. Gnnel, J. Phys.: Condens. Matter 5, 4343 (1993)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Max-Planck-Institute for Polymer Research, 55021, Mainz, Germany

    David Laroze & Harald Pleiner

  2. Instituto de Alta Investigación, Universidad de Tarapacá, Casilla 7D, Arica, Chile

    David Laroze

  3. Instituto de Física, P. Universidad Católica de Valparaiso, Casilla 4059, Valparaiso, Chile

    Javier Martinez-Mardones

Authors
  1. David Laroze
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Javier Martinez-Mardones
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Harald Pleiner
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to David Laroze.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Laroze, D., Martinez-Mardones, J. & Pleiner, H. Bénard-Marangoni instability in a viscoelastic ferrofluid. Eur. Phys. J. Spec. Top. 219, 71–80 (2013). https://doi.org/10.1140/epjst/e2013-01782-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1140/epjst/e2013-01782-6

Keywords

Search

Navigation