1 Introduction

The essence of quantum theory, that is, the interference of matter waves, stands out most clearly in the double-slit experiment for electrons [1]. However, it is also at the very heart of the Colella, Overhauser and Werner neutron interferometer [2], or its modern analogue in the Kasevich–Chu [3] atom interferometer. In both cases, the matter waves [4] experience a constant gravitational field. In the present paper, we report on an experiment that combines both features, that is multi-slit interference and a constant homogenous force. We employ surface gravity water waves [5] to perform a three-slit experiment [6] in the presence of a linear potential and analyse the results within the Bohm interpretation [7] of quantum mechanics. In particular, we measure the Bohm trajectories as well as the quantum potential for this system.

Quantum mechanics rests on a remarkable theoretical framework that calls into question our traditional intuitions regarding the behavior of particles. The approach of Erwin Madelung [8] and David Bohm [9, 10], tries to restore the classical notions and provides an alternative interpretation of quantum mechanics [7].

In Bohm’s formulation, the motion of a particle is governed by classical equations of motion [11] made possible by the inclusion of a supplementary potential, which is known as the quantum potential. Since it is determined by the wave function and brings about an intriguing deviation from classical mechanics, the particle provides its own guiding field. Hence, the quantum potential is an extremely important player in the process of molding the behavior of particles or waves by imposing forces that direct them on their paths.

Bohmian mechanics, which has recently attracted renewed interest, is discussed in a number of articles [12,13,14,15,16] and many interesting applications beyond interpretation issues have been proposed [17,18,19,20,21,22]. However, experimental detection of Bohm trajectories remains a formidable task [23]. To the best of our knowledge, there are only very few experiments that have reported their reconstruction, using for example weak measurements [24, 25] with either individual photons [26] or photon pairs that are entangled [27].

In this article, our focus is on the experimental examination of Bohmian mechanics within a classical context, specifically with surface gravity water waves in the presence of an external linear potential. This intriguing juxtaposition of quantum mechanical principles with a classical wave—and its empirical validation—becomes feasible due to three intrinsic attributes of surface gravity water waves: (i) Their governance by a wave equation that mirrors the Schrödinger one, (ii) the essential elements of Bohmian mechanics, such as trajectories and the quantum potential, and (iii) the capability to measure the magnitude and pinpoint the phase of a surface gravity water wave [28, 29].

Recently, we have studied experimentally [13] Bohmian mechanics for a classical system of freely propagating surface gravity water waves and have observed the corresponding Bohm trajectories and quantum potentials. However, it is interesting to investigate Bohmian mechanics in the presence of an external potential. The linear potential is an elementary example and at its core lies the cubic Kennard phase [30,31,32]. This phase captures the unique behavior of accelerating quantum particles and recent experiments have measured it [28, 29, 33, 34].

In this article, we break new ground by offering the first experimental evidence of Bohm trajectories and the quantum potential in a three-slit experiment with a linear potential, using the innovative medium of propagating surface gravity water waves. The linear potential results from a homogeneous and time-dependent flow created by a computer-controlled water pump. This approach not only sheds light on Bohmian mechanics but showcases the potential of water wave systems as analogues for probing intricate quantum behaviors.

Our brief article is organized as follows: In Sect. 2, we summarize the key features of Bohm trajectories and the quantum potential of surface gravity water waves for the special example of a time-dependent current providing us with a linear potential. We devote Sect. 3 to the discussion of our experimental results for the three-slit arrangement in the linear potential and conclude in Sect. 4 by a brief summary and an outlook.

2 Bohm trajectories and quantum potential of surface gravity water waves

In the co-moving frame, the normalized amplitude \(A\equiv A(\tau , \xi )\) of the envelope of a surface gravity water wave with low steepness moving in an external flow, satisfies the propagation equation [35]

$$\begin{aligned} i\frac{\partial A}{\partial \xi }=\frac{\partial ^2 A}{\partial \tau ^2}+F\tau A \end{aligned}$$
(1)

which is similar to the one-dimensional time-dependent Schrödinger equation of a particle in a linear potential \(-F\tau\) corresponding to a constant “force” F, given by \(F\equiv -(\omega _0/\varepsilon ^3k_0^2)a_2\) [29]. Here, \(a_{2}\) denotes the acceleration of the water flow in the laboratory frame.

We emphasize that the roles of time and space are interchanged with respect to those used in quantum mechanics [5, 36]. Indeed, the scaled dimensionless variables \(\xi\) and \(\tau\) are related to the propagation coordinate x and the time t by \(\xi \equiv \varepsilon ^2 k_0x\) and \(\tau \equiv \varepsilon \omega _0\left( x/c_g-t\right)\). The parameter \(\varepsilon \equiv k_0 a_0\) characterizing the wave steepness is assumed to be small, that is \(\varepsilon \ll 1\), in order to ensure [28, 37] the linearity of the wave equation.

We note that the elevation of the surface gravity water wave is real, and connected to the complex envelope A by being its real part via the concept of an analytical signal. Hence, the imaginary part of A follows from the Hilbert transform [38, 39] of the real-valued elevation as outlined in Ref. [13].

Due to the interchange of time and space the guiding equation [9]

$$\begin{aligned} \frac{d}{d\xi } \overline{\tau }(\xi )=2Im \bigg \{ \frac{1}{A(\xi , \overline{\tau }(\xi ))} \frac{\partial }{\partial \tau } A\mid _{\tau = \overline{\tau }(\xi )} \bigg \} \end{aligned}$$
(2)

in terms of the complex-valued amplitude A and its time derivative determines the surface gravity water wave trajectories \(\overline{\tau }=\overline{\tau } (\xi )\).

Fig. 1
figure 1

Experimental setup to observe Bohm trajectories and the quantum potential of surface gravity water waves in a linear potential due to a time-dependent and homogeneous water current generated by a computer-controlled pump. On the top a we depict the basic idea whereas the photographs b–d show the key ingredients of the apparatus: The water tank (b) with the waves and the pipes of the computer-controlled pump, a capacitance-type wave-gauge c that measures the elevation of the wave created at one end of the tank by a computer-controlled wave maker, practically without disturbing the propagation dynamics, and the computer-controlled pump d which generates the time-dependent parabolic flow. From the collection of envelopes in time and space, we reconstruct the Bohm trajectories as well as the quantum potential

Full size image

Another way to obtain trajectories in a wave theory is motivated by classical mechanics and involves the quantum potential which for surface gravity water waves reads

$$\begin{aligned} Q=-\frac{1}{\mid A \mid } \frac{\partial ^2 }{\partial \tau ^2} \mid A \mid , \end{aligned}$$
(3)

where \(\mid A \mid\) is the absolute value of the water wave envelope \(A(\tau ,\xi )\) governed by Eq. (1).

For a more detailed comparison between Bohmian mechanics and surface gravity water waves, we refer to Table 1 and Ref. [13] where we reported on Bohm trajectories and the quantum potential for the double slit and Airy wave packets in the absence of a potential.

Table 1 Comparison between Bohmian mechanics in quantum mechanics and its adaptation to classical surface gravity water waves
Full size table
Fig. 2
figure 2

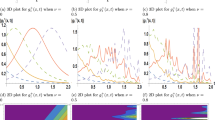
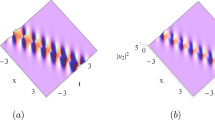
Three-slit experiment in a linear potential illustrated by the propagation of surface gravity water waves. On the top and the bottom we display the evolution of the envelope \(\mid A\mid\) and corresponding quantum potential Q. Bright and dark colors reflect high and low values, and the color bar units are millimeters. The Bohm trajectories indicated by dashed lines in the 2D-intensity plot underneath (a) and following from Eq. (2), are curved due to the acceleration caused by the linear potential. They run in the curved valleys of the landscape formed by the quantum potential (b). The tall mountain ranges lead to low amplitudes \(\mid A\mid\)

Full size image

3 Experimental realization

The experiments discussed in this article were performed in a \(5\,\textrm{m}\) long, \(0.4\,\textrm{m}\) wide, and \(h=0.19\,\textrm{m}\) deep laboratory wave tank shown in Fig. 1. Surface gravity water waves are generated by a computer-controlled wave maker placed at one end of the tank. Four capacitance-type wave gauges mounted on a bar measure the elevations of the surface gravity water waves at any location along the tank [28, 29]. For our experiments, they are placed at 6 different locations in the region of interest of 0.4–2.6 m to eliminate residual reflections from the absorbing beach placed at the other end of the water tank, resulting in 24 spatial coordinates.

We emphasize that the analysis of surface gravity water waves in an external potential is challenging since it requires precise control and monitoring of the external potential which is coordinated with the computer-controlled wave maker in synchronization of the water pump. Indeed, in Ref. [29], we have created such a linear potential in order to measure the Kennard phase. This potential was achieved by a time-dependent current opposite to the propagation direction of the wave packet.

We have used the carrier wave frequency \(\omega _{0}=15\) rad/s and the wave vector \(k_{0}=23\) 1/m which giving rise to a group velocity \(c_{g}=0.33\) m/s and satisfies the deep-water condition [5] \(k_{0}h>\pi\). The amplitude is \(a_{0}=4\) mm and thus, the corresponding steepness \(\varepsilon <0.1\) guarantees the validity of the linear Schrödinger equation. For an analysis of and experiments with nonlinear surface gravity water waves, we refer to [28, 37].

The dimensionless force F is obtained assuming that the wave packet follows a parabolic trajectory \(\langle t(x)\rangle = a_1 x + a_2 x^2\); \(a_{1}=c_{g}^{-1}\) being the inverse group velocity of the wave packet. The measured velocity parameter is \(a_{1}=3.07\,\mathrm{s/m}\) which is in good agreement with \(c_{g}^{-1}=3.06\,\mathrm{s/m}\) calculated using the water waves dispersion relation, and \(a_{2}=0.05\,\mathrm{s/m^{2}}\). This procedure yields \(F = -1.95\).

Figure 2 summarizes the key results of our three-slit experiment in a linear potential. We show the absolute value \(\mid A \mid\) of the wave-function analogue in a two- and three-dimensional representation together with the Bohm trajectories using Eq. (2), as well as the quantum potentials defined by Eq. (3). The complex amplitude envelope \(A\equiv |A|\exp (i\varphi )\) determines the variation in time and space of the surface elevation

$$\begin{aligned} \eta (t,x)\equiv a_0 A(t,x) \cos \left[ k_0x-\omega _0 t\right] \end{aligned}$$
(4)

including the carrier wave. The temporal variation \(A=A(t,x)\) of the initial surface elevations

$$\begin{aligned} A(t,x=0) \equiv a_{0} \bigg \{ \exp \left[ -t^{2}/t_{0}^{2} \right] +\exp \left[ -(t-t_{s})^{2}/t_{0}^{2} \right] + \exp \left[ -(t+t_{s})^{2}/t_{0}^{2} \right] \bigg \}, \end{aligned}$$
(5)

is a sum of three Gaussian wave packets, where each Gaussian represents a temporal slit. Here, \(t_{0}\) is the temporal width of the slits and \(t_{s}\) denotes the slit separation.

The experiments were performed for \(t_{0}=1.0\) s and \(t_{s}=3.3\) s. Hence, there is partial overlap between the wings of the three Gaussian lobes which leads to the appearance of additional features.

Figure 2 offers a detailed visualization of the Bohm trajectories in relation to the quantum potential and its influence on the trajectories. In Fig. 2a, we distinctly observe that the trajectories tend to bypass areas characterized by destructive interference. These regions correlate with zones where the quantum potential, shown in Fig. 2b, is notably high, suggesting a direct influence of the quantum potential in guiding the Bohm trajectories away from these areas. Conversely, areas of constructive interference attract these trajectories. These regions are marked by low values of the quantum potential, signifying a more favorable pathway for the trajectories.

A specific observation can be made at the point \(x=2.0\) m. Here, we witness an evident manifestation of destructive interference. The Bohm trajectories seem to recognize this zone as unfavorable, and hence navigate around it, avoiding it during their propagation. This behavior becomes even more elucidated when one examines Fig. 2b. where the quantum potential is mapped out, revealing a pronounced hill at the aforementioned point. This sharp rise in the quantum potential underscores the reason behind the trajectories’ avoidance of this region, further solidifying the intricate relationship between the Bohm trajectories and the quantum potential.

4 Conclusions and outlook

In this article, we have delved into the profound interplay between the Bohm interpretation—traditionally associated with the microscopic realm of quantum waves—and its manifestation in the macroscopic domain, using surface gravity water waves propagating in a linear potential as our model system. Our observations not only shed light on the Bohm trajectories of waves emerging from three-Gaussian slits but also allowed us to successfully measure the associated quantum potentials. This combined approach has given us a deeper understanding of the propagation dynamics, underscoring the subtle manner in which the quantum potential shapes wave propagation. The detailed visualizations generated from our experiments provide an illustrative account of Bohmian dynamics in action.

It is worth emphasizing that the techniques and findings presented in our research extend beyond the specific parameters of our experiments. Our setup is versatile: it is not restricted solely to the slit geometry we used, or the linear potential environment. The methodologies we have championed here can be effectively applied to a broader spectrum of macroscopic wave types, including electromagnetic and acoustic waves.

Looking ahead, we see a vast potential in using this system for an in-depth analysis of diverse wave packets. A notable example is the study of wave packets showcasing diffractive focusing, as discussed in [40]. Our study also hints at deep connections to more complex systems, such as the energy eigenfunctions of the inverted harmonic oscillator. This system offers insights into properties akin to those observed at an event horizon, as highlighted by [41].

Furthermore, while our present investigation is rooted in the domain of low-steepness waves with linear dynamics, future endeavors could examine the role and relevance of Bohm trajectories and the quantum potential in the context of high-steepness waves. This would pave the way for understanding the interplay between these trajectories and nonlinear effects, as alluded to in [28].