Periodic orbits in the restricted three-body problem for observations of the smaller primary

Abstract

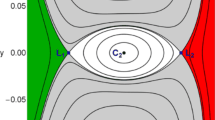
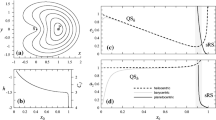
This work proposes a numerical investigation for periodic orbits in the restricted three-body problem to observe the smaller primary of the system. Periodic orbits are very important for observation missions, because they do not need station-keeping maneuvers and allow predicted passages by the main bodies. So, they allow a better observation of the body under study. For this verification, the grid search method will be used [(Barrio and Blesa, Chaos Solit Fractals, 41, 560–582 (2009)]. For each set of conditions, the differential equations of the motion of the spacecraft will be numerically integrated using TIDES [Abad et al., ACM Trans Math Softw (TOMS) 39, 1–28 (2012)]. In case of occurrence of periodic orbits, the characteristics of these orbits will be analyzed and the families found will be identified and classified. In particular, it is important to avoid effects from the close approach with the secondary body (swing-by), because this effect may destroy the periodicity of the orbit. This can be done using angle of approaches of 0$^\circ$ or 180$^\circ$ for the close approach, because they allow passages very close to the smaller body but with zero variations in energy and angular momentum. This aspect of the Swing-By maneuver is very important in the present research.