Skip to main content
SpringerLink
Log in

Numerical simulation of non-uniform heating due to magnetohydrodynamic natural convection in a nanofluid filled rhombic enclosure

  • Regular Article
  • Published:
The European Physical Journal Special Topics Aims and scope Submit manuscript

Abstract

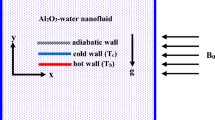
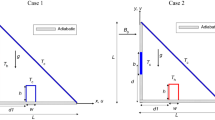
Numerical simulation of magnetohydrodynamic natural convection heat transfer in a rhombic enclosure of inclination angle \({\mathrm {45}}^{\mathrm {^{\circ }}}\) containing copper-water nanofluid has been presented in this paper. The top and bottom walls of the enclosure are subjected to non-uniform heating while left wall being subjected to lower temperature and right wall being maintained adiabatic. The finite element strategy (COMSOL Multiphysics) is used to solve the governing equations. The numerical simulations are done for the parametric values: 10\(^{4\, }\le \) Rayleigh number \(\le \) 10\(^{6}\); 0 \(\le \) Hartmann number \(\le \) 100; 0 \(\le \) volume fraction of nanofluid \(\le \) 0.05. The phase deviation angle (top wall) is varied in the range from 0 to \({\uppi }\) with amplitude of non linear heating being maintained constant. The motivation of this research goes with the fact that the associated transport phenomenon conveys the implication of designing an optimal thermal system analogous to the theme of non-uniform heating, with the phase angle being a crucial design parameter. The numerical results depict to the fact, that the rate of heat transfer follows non-monotonic trends and is considerably influenced by interplay of the phase shift angle, Rayleigh number and Hartmann number. The results showed that at Rayleigh number \(\ge 10^{5}\), the heat transfer rate gets inhibited by enhancing the magnetic field intensity. The impact of different types of nano particles is illustrated by comparing the results with the results of three different nanofluids, silver– water, titanium dioxide–water and diamond–water nanofluids.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

Abbreviations

\(\hbox {B}_{0}\) :

Magnetic field strength, N m\(^{-1}\)A\(^{-1}\)

\(\hbox {c}_{\mathrm{p}}\) :

Specific heat, Jkg\(^{-1}\)K\(^{-1}\)

L:

Enclosure length, m

g:

Acceleration due to gravity, ms\(^{-2}\)

h:

Heat transfer coefficient, Wm\(^{-2}\)K\(^{-1}\)

k:

Thermal conductivity Wm\(^{-1}\)K\(^{-1}\)

\(\hbox {Nu}_{\mathrm{l}}\) :

Local Nusselt number

\(\hbox {Nu}_{\mathrm{avg}}\) :

Average Nusselt number

p:

Pressure, Nm\(^{-2}\)

P:

Dimensionless pressure

Pr:

Prandtl number

Ra:

Rayleigh number

Ha:

Hartmann number

\(\hbox {T}_{\mathrm{h}}\) :

Temperature of heated walls, K

\(\hbox {T}_{\mathrm{c}}\) :

Temperature of cold walls of enclosure, K

u,v:

Velocity components in x and y directions, ms\(^{-1}\)

U,V:

Dimensionless velocity components in X and Y directions

x,y:

Cartesian coordinates

X,Y:

Dimensionless coordinates

\(\uprho \) :

Density of fluid, kgm\(^{-3}\)

\(\upalpha \) :

Thermal diffusivity, m\(^{2}\)s\(^{-1}\)

\(\upbeta \) :

Thermal expansion coefficient, K\(^{-1}\)

\(\upnu \) :

Kinematic viscosity, m\(^{2}\)s\(^{-1}\)

\(\uptheta \) :

Dimensionless temperature

\(\upvarphi \) :

Volume fraction

\(\upsigma \) :

Electrical conductivity, Sm\(^{-1}\)

\(\lambda \) :

The phase angle of the top wall of rhombic enclosure

\(\varPhi \) :

Inclination angle of rhombic enclosure

\(\varepsilon \) :

Amplitude parameter of top wall of rhombic enclosure

t:

Time

l:

Local

Avg.:

Average

References

  1. S. Kakac, W. Aung, R. Viskanta, Natural convection: fundamentals and applications (1985)

  2. A. Baïri, E. Zarco-Pernia, J.M. García de María, Appl. Therm. Eng. 63, 304 (2014)

    Article  Google Scholar 

  3. S.U.S. Choi, J. Eastman, Enhancing thermal conductivity of fluids with nanoparticles (1995)

  4. J. Eastman, S. Choi, S. Li, W. Yu, L. Thompson, Appl. Phys. Lett. 78, 718 (2001)

    Article  ADS  Google Scholar 

  5. Y. Xuan, W. Roetzel, Int. J. Heat Mass Transf. 43, 3701 (2000)

    Article  Google Scholar 

  6. N. Putra, W. Roetzel, S.K. Das, Heat Mass Transf. 39, 775 (2003)

    Article  ADS  Google Scholar 

  7. Y.-S. Lin, P.-Y. Hsiao, C.-C. Chieng, Int. J. Therm. Sci. 62, 56 (2012)

    Article  Google Scholar 

  8. K.S. Hwang, J.-H. Lee, S.P. Jang, Int. J. Heat Mass Transf. 50, 4003 (2007)

    Article  Google Scholar 

  9. H.F. Oztop, E. Abu-Nada, Int. J. Heat Fluid Flow 29, 1326 (2008)

    Article  Google Scholar 

  10. A.K. Santra, S. Sen, N. Chakraborty, Int. J. Therm. Sci. 47, 1113 (2008)

    Article  Google Scholar 

  11. E. Büyük Öğüt, Int. J. Therm. Sci. 48, 2063 (2009)

  12. B. Ghasemi, S. Aminossadati, Int. J. Therm. Sci. 49, 1 (2010)

    Article  Google Scholar 

  13. S. Parvin, A.J. Chamkha, Int. Commun. Heat Mass Transf. 54, 8 (2014)

    Article  Google Scholar 

  14. V. Krishan, in: V. Krishan (Ed.), Astrophysical Plasmas and Fluids (Springer Netherlands, Dordrecht, 1999), p. 117

  15. L. Zhang, M.M. Bhatti, E.E. Michaelides, M. Marin, R. Ellahi, Eur. Phys. J. Spec. Top. (2021)

  16. L. Zhang, M.M. Bhatti, A. Shahid, R. Ellahi, O.A. Bég, S.M. Sait, J. Taiwan Inst. Chem. Eng. 124, 98 (2021)

    Article  Google Scholar 

  17. M.M. Bhatti, L. Phali, C.M. Khalique, Arch. Appl. Mech. 91, 1683 (2021)

    Article  ADS  Google Scholar 

  18. S. Dutta, S. Pati, J. Thermophys. Heat Transf. 1 (2022)

  19. N.A. Shah, S. Wang, T. Elnaqeeb, H. Qi, 24, 45 (2021)

  20. N. Ali Shah, N. Ahmed, T. Elnaqeeb, M.M. Rashidi, J. Appl. Comput. Mech. 5, 150 (2019)

    Google Scholar 

  21. Y. Ma, R. Mohebbi, M.M. Rashidi, Z. Yang, M.A. Sheremet, Int. J. Heat Mass Transf. 130, 123 (2019)

    Article  Google Scholar 

  22. R.U. Haq, F.A. Soomro, T. Mekkaoui, Q.M. Al-Mdallal, Int. J. Heat Mass Transf. 121, 1168 (2018)

    Article  Google Scholar 

  23. B. Ghasemi, S.M. Aminossadati, A. Raisi, Int. J. Therm. Sci. 50, 1748 (2011)

    Article  Google Scholar 

  24. A.H. Mahmoudi, I. Pop, M. Shahi, Int. J. Therm. Sci. 59, 126 (2012)

    Article  Google Scholar 

  25. K.S. Al Kalbani, M.M. Rahman, S. Alam, N. Al-Salti, I.A. Eltayeb, Heat Transf. Eng. 39, 511 (2018)

    Article  ADS  Google Scholar 

  26. M.B. Ben Hamida, K. Charrada, Numer. Heat Transf. Part A: Appl. 67, 902 (2015)

  27. F. Moukalled, H. Diab, S. Acharya, Numer. Heat Transf. Part A: Appl. 24, 89 (1993)

  28. R. Anandalakshmi, T. Basak, Int. J. Heat Mass Transf. 55, 1325 (2012)

    Article  Google Scholar 

  29. R. Anandalakshmi, T. Basak, Eur. J. Mech. B. Fluids 41, 29 (2013)

  30. S. Dutta, N. Goswami, A.K. Biswas, S. Pati, Int. J. Heat Mass Transf. 136, 777 (2019)

    Article  Google Scholar 

  31. S. Dutta, N. Goswami, S. Pati, A.K. Biswas, J. Therm. Anal. Calorim. 144, 1493 (2021)

    Article  Google Scholar 

  32. S. Dutta, S. Pati, L. Baranyi, Case Stud. Thermal Eng. 28, 101507 (2021)

    Article  Google Scholar 

  33. T. Basak, S. Roy, T. Paul, I. Pop, Int. J. Heat Mass Transf. 49, 1430 (2006)

    Article  Google Scholar 

  34. S. Dutta, S. Pati, p. 1 (2021)

  35. M. Torki, N. Etesami, J. Therm. Anal. Calorim. 139, 1565 (2020)

    Article  Google Scholar 

  36. S. Zeinali Heris, M. Pour, O. Mahian, S. Wongwises, Int. J. Heat Mass Transf. 73, 231 (2014)

    Article  Google Scholar 

  37. Y. Hu, Y. He, C. Qi, B. Jiang, H. Inaki Schlaberg, Int. J. Heat Mass Transf. 78, 380 (2014)

    Article  Google Scholar 

  38. E. Khalili, A. Saboonchi, M. Saghafian, Int. J. Therm. Sci. 112, 82 (2017)

    Article  Google Scholar 

  39. X.-Q. Wang, A. Mujumdar, Br. J. Chem. Eng. 25, 613 (2008)

    Article  Google Scholar 

  40. K. Khanafer, K. Vafai, M. Lightstone, Int. J. Heat Mass Transf. 46, 3639 (2003)

    Article  Google Scholar 

  41. O. Abouali, G. Ahmadi, Appl. Therm. Eng. 36, 1 (2012)

    Article  Google Scholar 

  42. T. Elnaqeeb, Eur. Phys. J. Spec. Top. 228, 2695 (2019)

    Article  Google Scholar 

  43. H.C. Brinkman, J. Chem. Phys. 20, 571 (1952)

    Article  ADS  Google Scholar 

  44. J.C. Maxwell, A Treatise on Electricity and Magnetism (Clarendon Press, New York, 1873)

    MATH  Google Scholar 

  45. COMSOL Multiphysics v. 5.2. www.comsol.com. COMSOL AB, Stockholm, Sweden

  46. R.W.L. Perumal Nithiarasu, Kankanhalli N. Seetharamu, Fundamentals of the Finite Element Method for Heat and Mass Transfer (2016)

  47. M. Thangavelu, N. Nagarajan, R.-J. Yang, Heat Transf. Eng. 1 (2021)

  48. M. Sharifpur, A.B. Solomon, T.L. Ottermann, J.P. Meyer, Int. Commun. Heat Mass Transf. 98, 297 (2018)

    Article  Google Scholar 

  49. M.D. Massoudi, M.B. Ben Hamida, Eur. Phys. J. Plus 135, 1 (2020)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Elitte college of Engineering Karnamadpur (Affiliated with MAKAUT), Sodepur, Kolkata, West Bengal, 700113, India

    Shantanu Dutta

  2. Department of Mathematics, Faculty of Science, Zagazig University, Zagazig, 44519, Egypt

    Thanaa Elnaqeeb

  3. Department of Mathematics and Statistics, Faculty of Science, Taif University, Taif, 888, Saudi Arabia

    Thanaa Elnaqeeb

Authors
  1. Shantanu Dutta
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Thanaa Elnaqeeb
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Thanaa Elnaqeeb.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dutta, S., Elnaqeeb, T. Numerical simulation of non-uniform heating due to magnetohydrodynamic natural convection in a nanofluid filled rhombic enclosure. Eur. Phys. J. Spec. Top. 231, 2879–2900 (2022). https://doi.org/10.1140/epjs/s11734-022-00601-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1140/epjs/s11734-022-00601-x

Search

Navigation