1 Introduction

The negatively charged nitrogen-vacancy (NV−) centers in diamond have recently been shown to be a powerful tool for quantum optics, spintronics, magnetic sensing, nanoscale thermometry, and bioimaging applications [1, 2]. It is a 6-electron system with two unpaired spins in the ground state (a triplet) [3]. This color center is bright and photostable, and their spin levels can be optically detected by magnetic resonance (ODMR) at room temperature down to single molecule level [4]. These remarkable photophysical properties, together with the inherent biocompatibility of diamond, have attracted considerable attention for their use as quantum sensors at the interface of physics and biology. Notable examples include the application of NV− arrays in bulk diamond for magnetic spin imaging under ambient conditions with sub-cellular resolution [5] and the development of fluorescent nanodiamonds (FNDs) containing NV− ensembles into nanoscale thermometers in living cells [6]. A sensitivity as high as \(100~\mbox{mK/Hz}^{1/2}\) has been achieved with a single defect center acting as a luminescent thermometer [7].

To enhance the potential of NV− for temperature sensing [6–11], we have developed methods to conjugate FNDs with other nanoparticles such as gold nanorods (GNRs) to form multi-functional nanohybrids [12]. The NV-based quantum sensors consist of FNDs of ∼100 nm in diameter and their surfaces are carboxylated by strong oxidative acid washes [13]. The GNRs are ∼10 nm in diameter and ∼41 nm in length with a characteristic surface plasmon resonance (SPR) band at 808 nm [14]. They are excellent thermal transducers converting photon energy into heat and are well suited for hyperthermia applications [15, 16]. We prepare the hybrid nanoparticles by covalent conjugation of poly-L-arginine with the carboxylated FNDs through amide linkages [17], followed by physical adsorption of bare GNRs onto the amine-grafted FNDs through electrostatic forces. More than one GNR can be attached to the FND, making the nanohybrid an effective energy absorber and thus an efficient laser-activated nanoheater.

The development of the dual-functional GNR-FND hybrids enabled us to achieve highly localized heating of the samples of interest and simultaneously probe their temperature in situ at the nanoscale with the ODMR technique. We applied the nanohybrids in living cells both as a nanoscale heater as well as a nanoscale thermometer by using near-infrared (NIR) and green lasers for remote heating and probing, respectively. In addition, we demonstrated their utility for orientation tracking of the nanohybrids with or without laser heating in the presence of a magnetic field on a glass slide or in cells. Finally, to provide a better understanding of the nanoscale heating process, we conducted numerical simulations by solving steady-state heat conduction equations and illustrated the three-dimensional temperature profiles of the gold/diamond nanohybrids in aqueous media with a volume-equivalent sphere approximation for both GNR and FND.

2 Experimental section

2.1 Materials and chemicals

Synthetic type Ib diamond powders (Micron+) with a medium size of 140 nm were obtained from Element Six, GNRs surface-coated with the surfactant cetyltrimethylammonium bromide (CTAB) were from Nanopartz, Dulbecco’s modified Eagle’s medium (DMEM) was from Gibco-Invitrogen, LysoTracker Green was from Invitrogen, N-(3-dimethylaminopropyl)-\(N'\)-ethylcarbodiimide hydrochloride (EDC), N-hydroxysuccinimide (NHS), poly-L-arginine hydrochloride (PLA), bovine serum albumin (BSA), and all other chemicals were from Sigma-Aldrich and used without further purification.

2.2 FND production and surface modification

FNDs were produced by radiation-damage of synthetic diamond powders with a 40-keV He+ beam, followed by annealing at 800°C for 2 h and air oxidation at 450°C for 1 h [13]. The particles were then surface-functionalized with carboxyl groups in concentrated H2SO4-HNO3 (3:1, v/v) at 100°C for 3 h in a microwave reactor (Discover BenchMate, CEM). The carboxylated FNDs were finally separated by centrifugation and rinsed extensively with distilled deionized water (DDW).

FNDs were surface-coated with PLA by using water-soluble carbodiimide crosslinkers through amide bond formation [17], as illustrated in Figure 1(a). Briefly, carboxylated FNDs (1 mg) were thoroughly dispersed in DDW by sonication for 15 min. EDC (2 mg) and NHS (2 mg) were then added to the mixture for 30 min. After separation by centrifugation and cleaning with DDW, the FNDs were mixed with PLA (1 mg) for 2 h and washed with DDW to remove unbound PLA.

Figure 1
figure 1

Synthesis and characterization of GNR-FND nanohybrids. (a) Covalent conjugation of PLA with carboxylated FNDs through carboxyl-to-amine crosslinking by carbodiimide chemistry for physical adsorption of bare GNRs. (b) TEM image of PLA-coated FNDs decorated with 10-nm × 41-nm GNRs. (c) Comparison between the absorption spectra of 10-nm × 41-nm GNRs and the emission spectrum of 100-nm FNDs in water. Two vertical black bars indicate the sites of laser excitation at 532 and 808 nm.

Full size image

2.3 GNR-FND preparation

CTAB-coated GNRs were briefly washed with DDW to reduce the amount of surface-bound CTAB for exposure of their negatively charged surfaces. After the water wash, GNR (0.042 mg/ml, 2 ml) and PLA-FND (1 mg/ml, 0.1 ml) were mixed together by gentle shaking for 30 min, followed by differential centrifugation and collection of the pellets. Size distribution of the particles before and after conjugation was measured by a particle size and zeta potential analyzer (Delsa Nano C, Beckman-Coulter). Size, shape, and configuration of both GNRs and FNDs in the nanohybrids were visualized with a transmission electron microscope (H-7100, Hitachi).

2.4 Cell culture and GNR-FND labeling

HeLa cells were seeded at a density of \(2 \times 10^{5}\) cells per 35-mm dish in DMEM and incubated overnight at 37°C with 5% CO2 for cell attachment. Prior to cell labeling, the GNR-FND hybrids (5 mg) were first coated with BSA (1 mg) by physical adsorption through gentle vortex mixing of the reagents at room temperature for 2 h to prevent agglomeration of the particles in cell medium [18]. The BSA-coated GNR-FNDs were then suspended in serum-free DMEM at a concentration of 20 μg/ml. After sonication for 30 min, the BSA-coated GNR-FND suspension (1 ml) was added to the cell-containing dish for cellular uptake of the particles in an inverted configuration for 4 h [19]. The FND-labeled cells were then trypsinized, thoroughly washed with warm DMEM to remove free GNR-FNDs in solution, and re-cultured in fresh culture medium on glass coverslips overnight before being mounted on a microscope for fluorescence imaging.

2.5 Colocalization studies

GNR-FND-labeled HeLa cells incubated in phosphate-buffered saline (PBS) were stained with Hoechst 33342 and LysoTracker Green, following manufacturer’s instructions. After being washed with PBS, the cells were imaged by using a confocal laser scanning microscope (SP8, Leica) equipped with a white-light continuum laser. Wavelengths of the laser were selected with a prism for the excitation of Hoechst 33342, LysoTracker Green, and FND at 405, 504, and 532 nm, respectively. Their corresponding fluorescence emissions were collected at 461/40, 520/40, and >600 nm.

2.6 ODMR spectroscopy

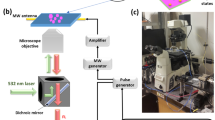
The experimental setup for temperature and magnetic field sensing consisted of a microscope (IX-71, Olympus) coupled with a diode-pumped solid-state laser (DPSS, Coherent) and a Ti-sapphire laser (3900S, Newport) operating at 532 nm and 808 nm, respectively, as detailed in [11]. The 532 nm light was first reflected by a long-pass dichroic mirror (545dcxr, Chroma) and then combined with the 808 nm light at the second short-pass dichroic mirror (725dcspxr, Chroma). They were then focused onto the samples on a glass coverslip via a 100× oil-immersion objective, which also served to collect FND fluorescence for detection. A three-dimensional confocal fluorescence tracking technique was implemented to ensure long-term observation of the same particle under investigation. To obtain the ODMR spectra, samples were excited with microwaves delivered via a thin gold wire (25 μm in diameter) connected to a microwave amplifier (5183, Ophir) and then a frequency synthesizer (PTS 3200, Programmed Test Sources). The wire was situated in close proximity to the glass coverslip, on which the specimen was prepared in a microchannel (∼1 mm height, ∼2 mm width, and ∼8 mm length) constructed with two glass bars, an adhesive frame, and high vacuum silicone grease. Both the microwave and the 532 nm probe laser were run in continuous-wave (CW) mode, and the fluorescence photons (675 ± 37 nm) were detected at each scanning microwave frequency by an avalanche photodiode (SPCM-AQR-15, Perkin Elmer). Two additional 808 nm laser notch filters were used to reduce the background noise level when collecting FND fluorescence in the presence of the NIR light. The spatial overlap between the heating and detection laser beams at the samples was examined with an electron multiplying charge-coupled device (IXON, Andor) for their scattered light images. A Gaussmeter (GM-2, AlphaLab) measured the strength of the magnetic field applied to the samples.

3 Results and discussion

3.1 Characterization of GNR-FNDs

CTAB is a commonly used surfactant to coat the surface of GNRs for morphological stabilization [20]. However, it is known that CTAB-encapsulated GNRs are cytotoxic and the toxicity is mainly caused by CTAB on the particles’ surface [21]. Repeated water wash effectively removes the CTAB coating but often results in agglomeration of the particles in suspension [22]. Being a carbon-based nanomaterial, FND can be easily surface-grafted with cationic polymers (such as PLA) to bind with bare GNRs, which are negatively charged, through electrostatic interactions after removal of the surfactant layer. This allows integration of the heating and temperature sensing functions into one unit by forming stable GNR-FND hybrids, although aggregation of GNRs on the surface of FNDs might occur. Figure 1(b) displays a typical transmission electron microscopy (TEM) image of the hybrid nanoparticles. Each FND can carry one or multiple GNRs with random orientation. As the absorption of light by the GNR at 532 nm is 6.2-fold weaker than that at 808 nm (Figure 1(c)), heating of the nanohybrids by the green laser excitation alone with an incident power of <10 μW is negligible. Moreover, quenching of the fluorescence by the adsorbate is insignificant due to the poor spectral overlap between the GNR absorption and the FND emission.

We first carried out ODMR measurements for the GNR-FND hybrids spin-coated on a glass coverslip at room temperature. A dip corresponding to the crystal field splitting (D) of the triplet ground state of NV− appeared at 2,868.4 MHz (Figure 2(a)). The two transitions, \(m_{\mathrm{s}} = 0 \rightarrow m_{\mathrm{s}} = \pm1\), observed in the spectrum are non-degenerate due to the presence of local crystallographic strains. When irradiated by a CW 808 nm laser in overlap with the 532 nm laser, the GNR-FNDs exhibited a distinct shift of the ODMR peaks toward lower frequencies, an indication of laser heating. Apart from the frequency red-shift, the ODMR peaks also exhibited a reduction in height. The peak heights of both transitions decreased steadily with the increase of the 808 nm laser power. The observation is in line with a previous study using 1,064 nm light for fast optical modulation of NV− fluorescence [23]. It is noted that with the simple physical adsorption method described above, about 60% of the FND particles could be successfully conjugated with GNRs. To reach 100% efficiency, more elaborate covalent conjugation methods should be applied.

Figure 2
figure 2

Laser heating and temperature sensing of a GNR-FND on a glass substrate. (a) Typical ODMR spectra of a spin-coated GNR-FND before and after heating by a CW 808 nm laser. The ODMR peak shifted to the lower frequency as the NIR laser power was increased from 0 to 1.8 mW. Dimensions of the GNRs are 10 nm × 41 nm. (b) Temperature rise of FND in the GNR-FND as a function of the 808 nm laser power. The temperature rise gradually leveled off as the laser power exceeded 0.8 mW, an indication of shape deformation of the GNR. Inset: A typical fluorescence image of the spin-coated particle (denoted by the yellow arrow) used to obtain the ODMR spectra. The image size is 10 × 10 μm2.

Full size image

Based on the thermal shift of the ODMR peak, \(\Delta D/\Delta T = -0.075\mbox{ MHz/K}\) [24], we plotted the temperature rise (\(\Delta T_{\mathrm{FND}}\)) of the FND particle against the NIR laser power (\(P_{\mathrm{NIR}}\)) in Figure 2(b). As noted, the \(\Delta T_{\mathrm{FND}}\) did not go linearly with \(P_{\mathrm{NIR}}\) but gradually leveled off at the laser power greater than 0.4 mW. To understand this nonlinear behavior, we allowed the temperature returning to the ambient value and then redid the heating experiments on the same nanohybrids under the same irradiation conditions. The levels of the temperature changes were found to be much reduced, indicating that it is not a result of excitation saturation which is a reversible effect. We thus concluded that this nonlinear behavior is most likely due to shape deformation of the 10-nm × 41-nm GNRs, which is known to occur at ∼100C and blue-shift the SPR bands [25, 26]. Such photothermally induced reshaping has been previously observed for GNR ensembles in aqueous media [25] and organic films [26] as well as for single GNRs embedded in between two membrane phases [27].

We may compare the presently developed NV-based thermometric method with the state-of-the-art temperature measurement using quantum dots (QDs) and gold nanoparticles [28, 29]. As luminescent nanothermometers, the highest spatial resolutions of FNDs and QDs are comparable, both limited by the diffraction of light. Although the detection of ODMR signals is very technically challenging, the ultimate sensitivity of the NV-based nanothermometry is about 3 orders of magnitude more sensitive, as recently reported by Kucsko et al. [6]. Other advantages of FNDs include that diamond is chemically inert and the internal NV− centers are well protected from surface imperfections and perturbations from the environment. As such, FNDs are more biocompatible and even more photostable than QDs. In addition to that, the dynamical range of the temperature sensing with NV− is much higher than that of QDs, and temperature measurements above 500 K have been successfully conducted for both bulk [7] and nanoscale [10] diamonds. Most recently, time-resolved nanothermometry with a temporal resolution of better than 10 μs has been achieved with 100-nm FNDs [11], which adds a new dimension to the use of NV− for temperature sensing applications.

3.2 GNR-FNDs for nanoscale heating and temperature sensing

The availability of GNR-FNDs with both heating and sensing functionalities enables active nanoscale thermometric measurement in cells and tissues by optical means. More importantly, it opens an opportunity to address questions concerning the optimization of the intensity and duration of heat shock in hyperthermia therapy [30]. To prove the concept, we introduced the dual-functional nanoparticles into HeLa cells through endocytosis, following standard protocols [18, 19]. Colocalization studies with confocal fluorescence microscopy and acidotropic probes (such as LysoTracker Green) confirmed that these particles were predominantly trapped in the lysosomes of the living cells (Figure 3(a)-3(d)) [31]. Illumination of the hybrid nanoparticles with the 808 nm laser resulted in highly localized heating. A significant temperature rise was observed at \(P_{\mathrm{NIR}} = 0.04\mbox{ mW}\) and it scaled nearly linearly with the laser power to \(\Delta T_{\mathrm{FND}} \sim 20\mbox{ K}\) at \(P_{\mathrm{NIR}} = 0.8\mbox{ mW}\) (Figure 3(e)). This temperature rise is more than sufficient for photothermal therapy applications and fine tuning of the temperature setting can be easily realized by adjusting the NIR laser power when needed.

Figure 3
figure 3

Nanoheating and in-situ temperature sensing of GNR-FNDs in cells. (a-c) Colocalization studies of internalized GNR-FNDs with lysosomes in HeLa cells by confocal fluorescence microscopy. The cells were fluorescently labeled with Hoechst 33342 (a), LysoTracker Green (b), and FND (c) markers. (d) Merged bright-field and fluorescence images of the cells. Yellow-coloured spots correspond to the colocalization of FNDs (red) with lysosomes (green). (e) Power-dependent temperature rises of two GNR-FND particles irradiated by an 808 nm laser with its power increasing from 0 to 0.8 mW in a HeLa cell.

Full size image

A question may arise: are the temperatures of the GNRs and FNDs in the nanohybrids the same or they markedly differ since only the GNRs are laser-heated? To address this issue, numerical simulations for the temperature profiles of a single GNR or multiple GNRs attached to a FND in water (or any physiological medium) have been performed using the heat conduction equation and a volume-equivalent sphere approximation for both GNR [32] and FND (Figure 4(a)). A finite element software (COMSOL, Multiphysics) numerically solves the partial differential equations (PDEs) describing the temperature profiles in three dimensions. For simplicity, the model takes only the laser-induced heat source and the conduction dissipation into consideration, assuming that there is no significant fluid dynamic flow. The steady state PDE solved for the individual medium (water, gold, or diamond) in the system is

$$ \nabla \cdot \bigl[ \kappa ( x,y,z ) \nabla T ( x,y,z ) \bigr] + \dot{Q} ( x,y,z ) =0, $$
(1)

where T and κ are the temperature and thermal conductivity of the medium and

$$ \dot{Q} ( x,y,z ) = \textstyle\begin{cases} \sigma I/V&\mbox{gold location}, \\ 0&\mbox{elsewhere}, \end{cases} $$
(2)

where σ and V are the absorption cross section and volume of GNR, respectively, and I is the laser intensity at the focus where the nanohydrid is irradiated. The domain used in this simulation model is a sphere of 10 μm radius and the domain boundary temperature is set to the heat bath temperature, \(T_{0}\). At the boundary between any two media (A and B), the COMSOL heat module automatically imposes the following interface boundary conditions to ensure the continuity of both temperature and heat flux,

$$\begin{aligned}& T_{\mathrm{A}} ( \overline{x}_{0} ) = T_{\mathrm{B}} ( \overline{x}_{0} ), \end{aligned}$$
(3)
$$\begin{aligned}& - \kappa_{\mathrm{A}} \frac{\partial T_{\mathrm{A}} ( \overline{x}_{0} )}{\partial \overline{x}} = - \kappa_{\mathrm{B}} \frac{\partial T_{\mathrm{B}} ( \overline{x}_{0} )}{\partial \overline{x}}, \end{aligned}$$
(4)

where \(\overline{x}\) is the outward unit normal vector. It should be noted that the solution of these PDEs is not unique and any arbitrary shift of \(T ( x,y,z )\) is also a solution. In fact, by choosing the heat bath temperature \(T_{0}\) to be 0, one can easily show that the value of the solution \(T ( x,y,z )\) at any point is linearly proportional to σ (or I). The immediate consequence following is that the temperature ratio at any two points \(T ( x_{1}, y_{1}, z_{1} ) /T ( x_{2}, y_{2}, z_{2} )\) is a constant, regardless of the value of σ (or I) used in the calculations as long as \(\sigma>0\). This is an important finding considering that the exact value of σ is not exactly known in experiments due to the lack of knowledge of the GNR orientation and particle number (n) on each FND. For the simplest case with a single GNR attached to a FND, the simulation predicts that the temperature rises of these two particles in the complex roughly differ by a factor of two or, more precisely, \(\Delta T_{\mathrm{GNR}} / \Delta T_{\mathrm{FND}} = 2.1\) (Figure 4(b)). There is virtually no temperature gradient within both the GNR and FND particles owing to the large thermal conductivity of the gold and diamond nanomaterials with \(\kappa_{\mathrm{G}} \sim 300\ \mathrm{W}/\mathrm{m}\cdot \mathrm{K}\) and \(\kappa_{\mathrm{D}} \sim 1\mbox{,}000\ \mathrm{W}/\mathrm{m} \cdot \mathrm{K}\), respectively.

Figure 4
figure 4

Numerical simulations of heat conduction. (a) Simulated three-dimensional temperature profile of a heated GNR-FND nanohybrid in water. The simulation was conducted with COMSOL based on a volume-equivalent sphere approximation for both FND and GNR with \(\sigma I = 7\mbox{ $\upmu$W}\). (b) Simulated distance dependence of the temperature rises along the symmetry axis (z-coordinate) of the heated GNR-FND nanohybrid with \(n = 1\). (c) Simulated distance dependence of the temperature rises along the symmetry axes of the heated GNR-FND nanohybrids with \(n = 1\mbox{-}10\) (bottom to top curves). Inset: Three-dimensional temperature profile of two GNR spheres anchored on the north and south poles of a FND sphere. Only a quarter of the temperature profile is shown. (d) Simulated temperature rises, \(\Delta T_{\mathrm{GNR}}\) and \(\Delta T_{\mathrm{FND}}\), and their ratios as a function of the number of GNRs attached to the FND.

Full size image

In cases where there is more than one GNR attached to the FND, we assume that the GNRs are evenly spaced at the equator of the FND sphere (inset in Figure 4(c)) to simplify the simulations. This assumption is justified by the fact that diamond has an exceptionally large thermal conductivity and no matter where the GNRs are attached to the FND surface, they all experience the same diamond temperature. With the nanohybrids irradiated under the same conditions as before (i.e. identical σ and I), we find that the temperature rise ratio decreases to \(\Delta T_{\mathrm{GNR}} / \Delta T_{\mathrm{FND}} = 1.5\) as the number of the GNRs increases to \(n = 2\) (Figure 4(c)). Interestingly, this ratio gradually decreases and approaches to \(\Delta T_{\mathrm{GNR}} / \Delta T_{\mathrm{FND}} \sim 1\) at a large n (Figure 4(d)), where the temperature becomes nearly uniform over the entire hybrid nanoparticle. Since our synthesized nanohybrids often contain multiple GNRs as shown in Figure 1(b), the simulation leads us to conclude that the temperature rises of the GNRs and FND in each nanohybrid should not differ by more than a factor of 2 when they are immersed in water or trapped in cells. The determination of this upper bound on the GNR temperature serves as an important reference for the use of these hybrid nanoparticles in forefront applications.

3.3 GNR-FNDs for magnetic sensing and orientation tracking

The present temperature measurement with single GNR-FNDs is fully compatible with the presence of a static magnetic field. At high field strength, the ODMR peaks of the NV− ensembles in FNDs are expected to split into eight components since the tetrahedral structure of diamond dictates four possible orientations of the spin quantization axes in a single-crystal lattice [33–35]. Although the Zeeman splitting has an undesirable effect of reducing the ODMR contrast by about a factor of 4, the linewidth of each component is decreased by half compared with that of the major peak in the field-free region. These two effects combined give rise to similar sensitivity on the temperature measurements with or without the magnetic field. Figure 5(a) presents the result obtained for a GNR-FND spin-coated on a glass coverslip when exposed to a magnetic field derived from a permanent magnet (5 mm in length and 6 mm in diameter) situated ∼13 mm above the sample. Six resolved peaks appeared in the ODMR spectrum and each of them showed a significant thermal shift when the nanohybrid was exposed to the NIR light. Choosing one of the peaks with the largest contrast (i.e. the peak at 2,701.7 or 3,037.9 MHz), a measurement of its frequency shift at \(P_{\mathrm{NIR}}= 0 \mbox{-} 1.8\mbox{ mW}\) revealed a nonlinear temperature rise with the increasing laser power (Figure 5(b)). Again, the temperature started to level off at the laser power exceeding 1 mW, in accord with the previous finding (Figure 2(b)).

Figure 5
figure 5

ODMR spectroscopy for simultaneous temperature and magnetic field sensing. (a) Measurement of the ODMR spectra of a GNR-FND in the absence and presence of a static magnetic field with \(B = 6\mbox{ mT}\). (b) Thermal shifts of the peak at 2,701.7 MHz with the NIR laser power increasing from 0 to 1.8 mW under \(B = 6\mbox{ mT}\).

Full size image

The observation of the regular Zeeman splitting pattern (Figure 5(a)) similar to that of single crystal diamonds [36] reflects that the FNDs making up the nanohybrids are monocrystalline, despite that they are only of 100 nm in diameter. This characteristic allows us to employ the ODMR peak positions to deduce the angles between the magnetic field and the NV axes as well as to determine the magnetic field strength at the nanoscale with high precision. According to Doherty et al. [35], the ODMR spectrum of a single NV− center in the presence of a magnetic field of \(B\ll D/ \gamma_{e}\) is split into two components with the frequencies as

$$ f_{\pm} =D+ \frac{3 \gamma_{e}^{2} B^{2}}{2D} \sin^{2} \theta_{B} \pm \gamma_{e} B \cos \theta_{B} \sqrt{1+ \frac{\gamma_{e}^{2} B^{2}}{4 D^{2}} \tan^{2} \theta_{B} \sin^{2} \theta_{B}}, $$
(5)

where D is the crystal field splitting, \(\theta_{B}\) is the angle between the magnetic field and the center’s major symmetry axis, and \(\gamma_{e} = g_{e} \mu_{B} /h= 28.03\mbox{ MHz/mT}\) with \(g_{e} \sim 2.003\), \(\mu_{B}\) being the Bohr magneton, and h being the Planck constant. Using \(D = 2\mbox{,}869.4\mbox{ MHz}\) and the six frequencies given in Figure 5(a), we determined \(B = 6.0\pm0.2\mbox{ mT}\), which can be compared with \(B \sim 5.2\mbox{ mT}\) measured by a Gaussmeter at the sample position. The angle between the applied B field and the symmetry axis of the NV− center that yields the resonances at \(f_{+} = 3\mbox{,}037.9\mbox{ MHz}\) and \(f_{-} = 2\mbox{,}701.7\mbox{ MHz}\) is \(\theta_{B} = 9.3{}^{\circ}\). This angle did not change significantly with time (\(\Delta\theta_{B} < 1{}^{\circ}\)) even under continuous NIR laser irradiation at \(P_{\mathrm{NIR}} = 0.4\mbox{ mW}\), suggesting that the GNR-FND particle was firmly attached to the glass surface.

Finally, we have also made an attempt to apply this new tool for orientation tracking of the GNR-FND particles in HeLa cells. Again, the change in angle is small (\(\Delta\theta_{B} < 2{}^{\circ}\)) under the same NIR laser irradiation over 30 min. The result matches well with a previous study using single NV centers in 45-nm diamonds, showing a variation of the particle’s orientation by only 10° over 16 h in living cells [37]. The resistance to rotation is in line with our observation in Figure 3(d) that the particles are entrapped in the endocytic vehicles of the cells and become essentially immobile [13]. In future experiments, we will apply the technique to living organisms such as Caenorhabditis elegans, for which recent studies have shown that the FND particles can migrate between cells [38] and rotate quite freely [39] in the intestine of the worms.

4 Conclusion

We have developed FND and GNR into a two-in-one optical heating and sensing nanoplatform with simple surface chemistry. Our results suggest that the GNR-FND nanohybrids are useful for simultaneous temperature and magnetic sensing in biological platforms where the nanohybrids may find practical applications. Further improvement of the performance of the nanoscale sensors is possible by covalent conjugation of the surface-modified GNRs with FNDs through amide or other linkages, such as the azide-alkyne coupling by click chemistry [40]. GNR particles of different aspect ratios (and thus different SPR band shifts) can also be conjugated with the FNDs using similar strategies. These dual-functional GNR-FND nanoparticles are convenient and appealing for applications in nanoscale hyperthermia where highly localized and controlled heating for safer and more effective therapy of cancer is desired. On occasions where no knowledge of temperature is needed, the FNDs in the nanohybrids are still useful as a photostable beacon to guide researchers to achieve target-specific optical transfection [41] or light-activated therapies [42] with the constituting GNR nanoheaters.