Dynamic and static dipole polarizability of an Aharonov–Bohm ring

Abstract

The properties of nanoscale rings are sensitive to Aharonov–Bohm fluxes threading the ring. In particular, neighboring angular momentum eigenstates become degenerate in cases of half-integer flux. Such degeneracies have a profound effect on the dipole polarizability leading to a divergent response. We analyze circular finite-width nanorings and derive a simple and compact expression for the polarizability valid for arbitrary ring geometry, frequency and magnetic flux. The dipole response is significantly reduced by finite-width effects, yet divergencies at half-integer flux are predicted irrespective of width. Finally, a non-divergent (but large) response is restored through a non-perturbative treatment of both magnetic and electric fields.

1 Introduction

The Aharonov–Bohm (AB) effect [1,2,3,4,5,6,7,8,9,10,11,12,13,14] is an essential quantum phenomenon demonstrating the influence of magnetic fields in field-free spatial regions provided the associated vector potential is nonvanishing. The prototypical scenario is that of an infinitely long uniform solenoid that only produces an internal magnetic field but, crucially, implies an external vector potential decaying as $1/r$ with the distance r from the center of the solenoid [1]. The AB effect manifests itself as an orientation dependent phase such that a quantum wave split into parts circulating the solenoid in opposite directions will experience detectable flux-dependent interference [1]. Hence, experimental tests of the AB effect have been based on detection of interference oscillations in transport and magnetoresistance [2,3,4,5].

Electrons bound to a nanoscale ring threaded by an AB flux could potentially reveal AB effects in several ways other than transport interference. Importantly, bound-state energies and eigenstates vary with AB flux, and all derived properties could serve as probes of AB effects on bound states. Theoretical proposals suggested to probe such effects have been based on dipole moments [7, 10] and magneto-polarizability [8, 9]. Moreover, the effect on excitons [11, 12] and massless electrons in graphene [13] has been analyzed. Previous work, however, has been either purely numerical [8,9,10] or restricted to one-dimensional rings with vanishing width [7]. In the present work, we examine dipole polarizabilities as means to gauge bound-state AB effects taking into account the finite width of realistic nanorings as well as finite frequencies of the probe field. Thus, we envision a ring geometry such as illustrated in Fig. 1. Here, electrons are confined to a radial region between inner and outer radii $R_{{{\text{inner}}}} = \rho R$ and $R_{{{\text{outer}}}} = R$ in a two-dimensional ring with negligible vertical thickness. A dipole is induced by a time-dependent in-plane electric field. We assume perfect hard-wall confinement such that Dirichlet boundary conditions apply at $r = \left\{ {\rho R,R} \right\}$. Also, the cylindrical symmetry of this setup means that angular momentum l is a good quantum number. The simplicity of the model allows us to derive analytical and compact results for the induced dipole moment valid for arbitrary flux, frequency and radial ratio $\rho$.

Fig. 1

Nano-scale ring threaded by a central magnetic field and polarized by a perpendicular electric field. Inner and outer radii are $R_{{{\text{inner}}}} = \rho R$ and $R_{{{\text{outer}}}} = R$, respectively

In a weak horizontal electric field $\vec{\mathcal{B}}$ oscillating with frequency $\omega$, electrons are polarized as described by the induced dipole moment $d = \alpha \left( \omega \right)\mathcal{E}$, where $\alpha \left( \omega \right)$ is the polarizability. This effect has previously been discussed for AB rings in the limit of ideal rings with vanishing width [7] and numerically for finite width [8,9,10]. In the present work, we retain a finite width and, furthermore, derive a completely analytical expression for the polarizability valid for arbitrary AB flux, optical frequency and geometry. In standard perturbation theory, the polarizability of a state n is given by the sum-over-states expression $\alpha \left( \omega \right) = \sum\nolimits_{m \ne n} {g_{nm} /[ {( {E_{mn}^{(0)} } )^{2} - \omega^{2} }]}$, where $g_{nm}$ is the oscillator strength of the $n \to m$ transition and $E_{mn}^{\left( 0 \right)} = E_{m}^{\left( 0 \right)} - E_{n}^{\left( 0 \right)}$ the transition energy between unperturbed states, i.e., eigenstates in the absence of $\mathcal{E}$. Obviously, a large static polarizability $\alpha \left( 0 \right)$ can be expected if energies can be tuned such that a degeneracy $E_{m}^{\left( 0 \right)} \approx E_{n}^{\left( 0 \right)}$ can be achieved for some m. This is precisely the case in an AB ring, where energy levels for angular momenta l and $l \pm 1$ become degenerate if the magnetic flux is $\Phi = - \left( {l \pm \tfrac{1}{2}} \right)\Phi_{0}$ with $\Phi_{0} = h/e$ the flux quantum. Since, furthermore, transitions between angular momentum states l and $l \pm 1$ are dipole allowed, we anticipate a dramatic effect of the AB flux $\Phi$ on the polarizability.

The traditional sum-over-states approach is problematic if exact results are sought as one inevitably needs to truncate the sum. Below, we consequently use exact Dalgarno–Lewis perturbation theory [15,16,17,18,19,20,21,22] to circumvent the sum-over-states route to computing $\alpha (\omega )$. Hence, via the exact closed-form solution to an inhomogeneous perturbation problem, we are able to derive a simple and compact exact expression for $\alpha \left( \omega \right)$, valid for arbitrary flux $\Phi$, frequency $\omega$ and nanoring geometry $R_{{{\text{inner}}}} /R_{{{\text{outer}}}}$. We demonstrate that, indeed, $\alpha (0)$ diverges in the limit of half-integer flux $\Phi \to \left( {n + \tfrac{1}{2}} \right)\Phi_{0}$, where n is an integer. This finding demonstrates that $\alpha \left( {\omega \approx 0} \right)$ is a sensitive measure of AB effects on bound states in nanosystems. Obviously, however, a divergent polarizability signals a breakdown of some underlying assumption. Thus, non-perturbative inclusion of finite electric fields lifts the degeneracy responsible for the divergence. Yet, the polarizability near avoided crossings at $\Phi = - \left( {l \pm \tfrac{1}{2}} \right)\Phi_{0}$ is greatly enhanced relative to the $\Phi = 0$ case.

2 Theory

Before turning to the perturbation by the electric field, we study the properties of unperturbed states. The problem at hand is similar to, but actually simpler than, the case of a constant magnetic field, which is solvable in terms of Laguerre and hypergeometric functions [23]. Thus, a delta-localized magnetic field of the form $\vec{\mathcal{B}} = \hat{z}\delta \left( r \right)\Phi /\left( {2\pi r} \right)$ corresponds to a vector potential $\vec{\mathcal{A}} = \hat{z}\delta \left( r \right)\Phi /\left( {2\pi r} \right) = \hat{\theta }\Phi /\left( {2\pi r} \right)$, where $\hat{\theta }$ is a unit vector in the angular direction [1]. In contrast, a constant magnetic field implies a vector potential $\vec{\mathcal{A}} \propto r$. Throughout, we use atomic units measuring distances and energies in units of Bohr radii and Hartrees, respectively. An effective mass could readily be allowed for and leads to a simple rescaling of Bohr radius and Hartree unit. In atomic units, the flux quantum is $\Phi_{0} = 2\pi$ and the 2D AB-Stark Hamiltonian reads as $H = H_{0} + H_{1}$ with

$$ H_{0} = - \frac{1}{2}\nabla^{2} + V\left( r \right) + \frac{\Phi }{{\Phi_{0} r^{2} }}\hat{l}_{z} + \frac{{\Phi^{2} }}{{2\Phi_{0}^{2} r^{2} }},\;H_{1} = \mathcal{E}r\cos \theta \cos \left( {\omega t} \right).$$

(1)

Here, $\hat{l}_{z} = - i\partial /\partial \theta$ is the angular momentum with $\theta$ the angle to the electric field axis. The hard-wall boundary conditions mean that the potential V vanishes if $\rho R < r < R$ and is infinite otherwise. Note that the model would remain valid for nanorings having a finite height as nothing in Eq. (1) couples to motion in the z-direction. Hence, the Hamiltonian Eq. (1) is in principle applicable to all conducting nanorings with well-defined (effective) mass such that the kinetic energy is of the Schrödinger form $- \nabla^{2} /2$. Conversely, Dirac materials such as graphene are not necessarily well described by this model.

We write angular eigenfunctions as $\Theta_{l} \left( \theta \right) = e^{il\theta } /\sqrt {2\pi }$. Thus, we find normalized unperturbed $\left( {\mathcal{E} = 0} \right)$ states $\varphi_{ln}^{\left( 0 \right)} \left( {\vec{r}} \right) = \varphi_{ln}^{\left( 0 \right)} \left( r \right)\Theta_{l} \left( \theta \right)$ satisfying

$$ \left\{ { - \frac{1}{2}\left( {\frac{{{\text{d}}^{2} }}{{{\text{d}}r^{2} }} + \frac{1}{r}\frac{{\text{d}}}{{{\text{d}}r}}} \right) + V\left( r \right) + \frac{{\left( {l + \Phi /\Phi_{0} } \right)^{2} }}{{2r^{2} }}} \right\}\varphi_{ln }^{\left( 0 \right)} \left( r \right) = E_{ln }^{\left( 0 \right)} \varphi_{ln }^{\left( 0 \right)} \left( r \right). $$

(2)

It is convenient to introduce the shifted angular momentum $L \equiv l + \Phi /\Phi_{0}$ and radial wavenumber $k_{Ln}$ such that energies are $E_{ln}^{(0)} = k_{Ln}^{2} /\left( {2R^{2} } \right)$. Also, we need the combinations

$$ \begin{gathered} W_{l} \left( {k,x} \right) = Y_{l} \left( k \right)J_{l} \left( {kx} \right) - J_{l} \left( k \right)Y_{l} \left( {kx} \right), \\ W_{l}^{ \pm } \left( {k,x} \right) = \pm \left\{ {Y_{l} \left( k \right)J_{l \pm 1} \left( {kx} \right) - J_{l} \left( k \right)Y_{l \pm 1} \left( {kx} \right)} \right\}, \\ \end{gathered} $$

(3)

of Bessel functions of first and second kind. Then, the unperturbed eigenstates are [14]

$$ \varphi_{ln}^{\left( 0 \right)} \left( r \right) = N_{ln} W_{L} \left( {k_{Ln} ,\tfrac{r}{R}} \right),\;N_{ln} = \frac{{\pi k_{Ln} J_{L} \left( {\rho k_{Ln} } \right)}}{{R\sqrt {2\left[ {J_{L}^{2} \left( {\rho k_{Ln} } \right) - J_{L}^{2} \left( {k_{Ln} } \right)} \right]} }}. $$

(4)

By construction, the boundary condition at the outer radius $R_{{{\text{outer}}}} = R$ is automatically satisfied. However, to satisfy the inner one, the wavenumber $k_{Ln}$ must be a root of the Bessel combination $W_{L} \left( {k,\rho } \right)$. We stress that the order L is generally non-integer and depends on the magnetic flux. Also, $n = 1,2,3, \ldots$ is a radial index labeling the different roots in increasing order. In Fig. 2, we display the roots for the case $\rho = 0.2$. For clarity, only five different angular momenta $l \in \left[ { - 2,2} \right]$ are shown but the full pattern repeats periodically with integer values of the normalized flux $\Phi /\Phi_{0}$. In the range of weak magnetic fields, $|\Phi /\Phi_{0} | < \tfrac{1}{2}$, the ground state is $l = 0,n = 1$. Moreover, degeneracy with $l = \pm 1,n = 1$ states occurs at $\Phi /\Phi_{0} = \mp \tfrac{1}{2}$.

Fig. 2

Bound-state wavenumbers of an AB ring. For clarity, only states with angular momentum $l \in [ - 2,2]$ are shown

In weak fields, an approximate solution with $k_{0n}$ a root of $W_{0} \left( {k,\rho } \right)$ is

$$ \begin{aligned} k_{Ln} & \approx k_{0n} + L^{2} \frac{{\pi k_{0n} J_{0} \left( {k_{0n} } \right)J_{0} \left( {k_{0n} \rho } \right)}}{{4\left[ {J_{0}^{2} \left( {k_{0n} \rho } \right) - J_{0}^{2} \left( {k_{0n} } \right)} \right]}} \\ & \quad \times \left\{ {J_{0} \left( {k_{0n} } \right)\partial_{l}^{2} Y_{0} \left( {k_{0n} \rho } \right) + Y_{0} \left( {k_{0n} \rho } \right)\partial_{l}^{2} J_{0} \left( {k_{0n} } \right) - J_{0} \left( {k_{0n} \rho } \right)\partial_{l}^{2} Y_{0} \left( {k_{0n} } \right) - Y_{0} \left( {k_{0n} } \right)\partial_{l}^{2} J_{0} \left( {k_{0n} \rho } \right)} \right\}. \\ \end{aligned} $$

(5)

Here, $\partial_{l}^{2}$ designates the second derivative with respect to order, i.e., $\partial_{l}^{2} J_{0} \left( x \right) = \left. {\partial_{l}^{2} J_{l} \left( x \right)} \right|_{l = 0}$. Such derivatives, unfortunately, can only be expressed in terms of complicated hypergeometric functions and Eq. (5) is therefore of little practical use. It shows, however, that the lowest wavenumber correction, and therefore the energy, is quadratic in L.

3 Dipole polarizability

We now include the dipole interaction $\mathcal{E}r\cos \theta \cos \left( {\omega t} \right)$ to describe perturbation by the electric field. The Dalgarno–Lewis approach relies on expansions in the electric field [15,16,17,18,19,20,21,22]. Hence, to first order in the field, we write

$$ \varphi_{ln} \left( {\vec{r},t} \right) = \varphi_{ln}^{\left( 0 \right)} \left( {\vec{r}} \right)\exp \left( { - iE_{ln}^{\left( 0 \right)} t} \right) + \tfrac{1}{2}\mathcal{E}\varphi_{ln}^{\left( 1 \right)} \left( {\vec{r},\omega } \right)\exp \left( { - i\left( {E_{ln}^{\left( 0 \right)} + \omega } \right)t} \right) + \left( {\omega \to - \omega } \right). $$

(6)

Writing $E_{ln}^{(0)} + \omega \equiv k_{\omega }^{2} /(2R^{2} )$ and collecting first-order terms, we have $\left\{ {H_{0} - k_{\omega }^{2} /\left( {2R^{2} } \right)} \right\}\varphi_{ln}^{(1)} \left( {\vec{r},\omega } \right) + r\cos \theta \varphi_{ln}^{(0)} \left( {\vec{r}} \right) = 0.$ Due to the angular coupling, the first-order correction is of the form $\varphi_{ln}^{(1)} \left( {\vec{r},\omega } \right) = \{ {\varphi_{ln}^{( + )} \left( {r,\omega } \right)\Theta_{l + 1} \left( \theta \right) + \varphi_{ln}^{( - )} \left( {r,\omega } \right)\Theta_{l - 1} \left( \theta \right)} \}/2$, where the radial parts satisfy

$$ \left\{ { - \frac{1}{2}\left( {\frac{{{\text{d}}^{2} }}{{{\text{d}}r^{2} }} + \frac{1}{r}\frac{{\text{d}}}{{{\text{d}}r}}} \right) + V\left( r \right) + \frac{{\left( {L \pm 1} \right)^{2} }}{{2r^{2} }} - \frac{{k_{\omega }^{2} }}{{2R^{2} }}} \right\}\varphi_{ln}^{\left( \pm \right)} \left( {r,\omega } \right) + r\varphi_{ln}^{\left( 0 \right)} \left( r \right) = 0. $$

(7)

Here, the potential V is the infinite radial well assumed in Eq. (2). For brevity, we suppress indices and write $k_{Ln} \equiv k$. It may then be verified that the solutions to Eq. (7) are

$$ \frac{{\varphi_{ln}^{\left( \pm \right)} \left( {r,\omega } \right)}}{{4kRN_{ln} }} = \frac{{W_{L \pm 1} \left( {k_{\omega } \rho ,\tfrac{r}{\rho R}} \right)W_{L}^{ \pm } \left( {k,1} \right) - W_{L \pm 1} \left( {k_{\omega } ,\tfrac{r}{R}} \right)W_{L}^{ \pm } \left( {k,\rho } \right)}}{{\left( {k^{2} - k_{\omega }^{2} } \right)^{2} W_{L \pm 1} \left( {k_{\omega } ,\rho } \right)}} + \frac{{W_{L}^{ \pm } \left( {k,\tfrac{r}{R}} \right)}}{{\left( {k^{2} - k_{\omega }^{2} } \right)^{2} }} - \frac{{rW_{L} \left( {k,\tfrac{r}{R}} \right)}}{{2kR\left( {k^{2} - k_{\omega }^{2} } \right)}}. $$

(8)

The coefficients of the homogeneous solutions $W_{L \pm 1} (k_{\omega } ,\tfrac{r}{R})$ are adjusted to enforce Dirichlet boundary conditions. In turn, the polarizability $\alpha (\Phi ,\omega ) = \alpha_{ + } (\Phi ,\omega ) + \alpha_{ + } (\Phi , - \omega )$ follows from the radial integrals

$$ \alpha_{ + } \left( {\Phi ,\omega } \right) = - \frac{1}{2}\int\limits_{\rho R}^{R} {\varphi_{ln}^{\left( 0 \right)} \left( r \right)} \left\{ {\varphi_{ln}^{\left( - \right)} \left( {r,\omega } \right) + \varphi_{ln}^{\left( + \right)} \left( {r,\omega } \right)} \right\}r^{2} {\text{d}}r. $$

(9)

Evaluating such matrix elements requires definite integrals of Bessel function products with limits $r \in [\rho R,R]$. The corresponding generic indefinite integrals needed are listed in the appendix. Collecting all contributions is a tedious task that, fortunately, can be greatly reduced by symbolic mathematical software such as Mathematica. Also, recursion relations among Bessel functions as well as Wronskians are useful. Eventually, in terms of $\beta \equiv J_{L} \left( k \right)/J_{L} \left( {k\rho } \right)$, the full result can be reduced to the compact expression

$$ \begin{aligned} \alpha_{ + } \left( {\Phi ,\omega } \right) & = - \frac{1}{{2\omega^{2} }} + \frac{{k^{2} k_{\omega } \left\{ {\beta^{2} W_{L + 1}^{ - } \left( {k_{\omega } ,\rho } \right) + \rho W_{L}^{ + } \left( {k_{\omega } ,\rho } \right) - 4\beta /\left( {\pi k_{\omega } } \right)} \right\}}}{{4\omega^{4} R^{4} \left( {\beta^{2} - 1} \right)\rho W_{L + 1} \left( {k_{\omega } ,\rho } \right)}} \\ & \quad + \frac{{k^{2} k_{\omega } \left\{ {\beta^{2} W_{L - 1}^{ + } \left( {k_{\omega } ,\rho } \right) + \rho W_{L}^{ - } \left( {k_{\omega } ,\rho } \right) - 4\beta /\left( {\pi k_{\omega } } \right)} \right\}}}{{4\omega^{4} R^{4} \left( {\beta^{2} - 1} \right)\rho W_{L - 1} \left( {k_{\omega } ,\rho } \right)}}. \\ \end{aligned} $$

(10)

Here, the first term $- 1/\left( {2\omega^{2} } \right)$ originates from the last one in Eq. (8), whereas the terms proportional to $W_{L}^{ \pm } \left( {k,\tfrac{r}{R}} \right)$ in Eq. (8) yield a vanishing contribution. Several identities including $W_{L}^{ \pm } \left( {k_{\omega } \rho ,\rho^{ - 1} } \right) = W_{L \pm 1}^{ \mp } \left( {k_{\omega } ,\rho } \right)$ and $W_{L}^{ \pm } \left( {k_{\omega } ,\rho } \right) = W_{ - L}^{ \mp } \left( {k_{\omega } ,\rho } \right)$ can be applied to reformulate the result.

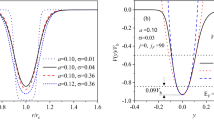
The result Eq. (10) is illustrated in Fig. 3 for a range of normalized fluxes $\Phi /\Phi_{0}$ approaching degeneracy $\Phi /\Phi_{0} = \tfrac{1}{2}$. In the low-frequency range $\omega R^{2} < 3$, the spectra evolve from a single resonance when $\Phi /\Phi_{0} = 0$ to a split doublet for $l \to l \pm 1$ transitions if $\Phi /\Phi_{0} \ne 0$. The oscillator strength of these resonances is seen to the nearly independent of $\Phi$. Hence, the single peak at $\Phi /\Phi_{0} = 0$ is roughly twice as intense as the individual split peaks whenever $\Phi /\Phi_{0} \ne 0$. Importantly, as $\Phi /\Phi_{0} \to \tfrac{1}{2}$, the lower resonance approaches the zero frequency limit $\omega \approx 0$. This is the expected behavior as the implied degeneracy between $E_{ln}^{(0)}$ and $E_{l - 1,n}^{(0)}$ translates into a divergent static polarizability.

Fig. 3

Dynamic polarizability of an AB ring with $\rho = 0.3$ and various flux values as indicated by color. An imaginary part $i0.05R^{2}$ is added to the frequency to regularize singularities

In the static limit $\omega \to 0$,

$$ \frac{\alpha (\Phi ,0)}{{R^{4} }} = \frac{{4(1 - L^{2} ) + k^{2} }}{{6k^{4} }} + \frac{{\beta^{2} (1 - \rho^{2} )}}{{24k^{2} (\beta^{2} - 1)}}\left( {\frac{{3k(1 - \rho^{2} )J_{L} (k\rho )}}{{\beta J_{L + 1} (k) - \rho J_{L + 1} (k\rho )}} - \frac{{3k(1 - \rho^{2} )J_{L} (k\rho )}}{{\beta J_{L - 1} (k) - \rho J_{L - 1} (k\rho )}} - 4} \right). $$

(11)

Note that all factors involving Bessel functions of the second kind $Y_{L}$ have been eliminated using Wronskian relations. We have verified that this expression agrees with the result derived directly from stationary perturbation theory. As they stand, Eqs. (10) and (11) are valid only if $|L| < \tfrac{1}{2}$. However, because the ground state polarizability repeats periodically in L, with unit period, all other cases are readily mapped to $|L| < \tfrac{1}{2}$.

A number of special cases can now be extracted. Firstly, in the limit of a very thin ring $\rho \to 1$, the lowest wavenumber diverges as $k_{L1} \to \pi /\left( {1 - \rho } \right)$ and the (low-frequency) polarizability is $\alpha_{ + } \left( {\Phi ,\omega } \right) = \left( {1 - 2\omega R^{2} } \right)R^{4} /[ {\left( {1 - 2\omega R^{2} } \right)^{2} - 4L^{2} } ]$. The static limit $\alpha \left( {\Phi ,0} \right) = 2R^{4} /\left( {1 - 4L^{2} } \right)$ is readily seen to agree with the two-dimensional rigid rotor [24], i.e., the Hamiltonian Eq. (1) with an infinite delta-potential such that radial motion is frozen at $r = R$. Secondly, in the special case of vanishing magnetic field $\Phi = L = 0$, Eq. (11) reduces to

$$ \frac{{\alpha \left( {0,0} \right)}}{{R^{4} }} = \frac{{4 + k_{0n}^{2} }}{{6k_{0n}^{4} }} + \frac{{\left( {1 - \rho^{2} } \right)J_{0}^{2} \left( {k_{0n} } \right)}}{{12k_{0n}^{2} \left\{ {J_{0}^{2} \left( {k_{0n} } \right) - J_{0}^{2} \left( {k_{0n} \rho } \right)} \right\}}}\left\{ {\frac{{3k_{0n} \left( {1 - \rho^{2} } \right)J_{0}^{2} \left( {k_{0n} \rho } \right)}}{{J_{0} \left( {k_{0n} } \right)J_{1} \left( {k_{0n} } \right) - \rho J_{0} \left( {k_{0n} \rho } \right)J_{1} \left( {k_{0n} \rho } \right)}} - 2} \right\}. $$

(12)

The first term agrees with the result of a disk [21, 22], in which $k_{0n} = \lambda_{0n}$, the n’th root of the Bessel function $J_{0} \left( x \right)$ such that $J_{0} \left( {k_{0n} } \right) = 0$ and the second term in Eq. (12) vanishes. In Fig. 4, the ground state polarizability is clearly seen to diverge as $\Phi /\Phi_{0} \to \tfrac{1}{2}$. Also, $\alpha \left( {\Phi ,0} \right)/R^{4}$ is monotonically increasing with $\rho$, approaching $2/\left( {1 - 4L^{2} } \right)$ in the case of thin rings. The pronounced dependence on $\rho$ demonstrates that finite-width effects must be accounted for in quantitative estimates of the nanoring polarizability. The divergence testifies to the sensitivity of $\alpha ( {\Phi ,\omega \approx 0} )$ as a practical measure of AB effects in bound electron systems.

Fig. 4

Ground state static polarizability versus magnetic flux for rings of varying ratio between inner and outer diameter $\rho$. Note the logarithmic scale and the divergence as $\Phi /\Phi_{0} \to \tfrac{1}{2}$. Circles are numerical results for a finite field $\mathcal{E}R^{3} = 0.05$

We will now address the (unphysical) assumption behind a divergent polarizability. Incidentally, relativistic effects, i.e., spin–orbit coupling, do not lift the degeneracy among l and $l \pm 1$ states. In fact, an analysis using infinite-mass boundary conditions [20] to enforce confinement is readily made and demonstrates that degeneracies persist, albeit shifted away from $\Phi = - \left( {l \pm \tfrac{1}{2}} \right)\Phi_{0}$. The actual reason, as discussed by other authors, lies in the treatment of the electric field as a weak perturbation. Thus, a non-perturbative solution lifts all degeneracies [7, 10, 25]. Degenerate perturbation theory in the subspace $\{ {\varphi_{ln}^{(0)} ,\varphi_{l \pm 1,n}^{(0)} } \}$ readily demonstrates this fact. To this end, one can show using integrals from the appendix that the associated dipole matrix element is

$$ \left\langle {\varphi_{ln}^{(0)} } \right|x\left| {\varphi_{l \pm 1,m}^{(0)} } \right\rangle = \frac{{2Rk_{Ln} k_{L \pm 1,m} \left\{ {\rho J_{L} \left( {k_{Ln} \rho } \right)J_{L \pm 1} \left( {k_{L \pm 1,m} \rho } \right) - J_{L} \left( {k_{Ln} } \right)J_{L \pm 1} \left( {k_{L \pm 1,m} } \right)} \right\}}}{{\rho \left( {k_{Ln}^{2} - k_{L \pm 1,m}^{2} } \right)^{2} \sqrt {J_{L}^{2} \left( {k_{Ln} \rho } \right) - J_{0}^{2} \left( {k_{Ln} } \right)} \sqrt {J_{L \pm 1}^{2} \left( {k_{L \pm 1,m} \rho } \right) - J_{L \pm 1}^{2} \left( {k_{L \pm 1,m} } \right)} }}. $$

(13)

Taking the limits $L \to 1/2$ and $m \to n$ reduces to the exceedingly simple result $\langle {\varphi_{0n}^{(0)} } \left|x\right| {\varphi_{ - 1,n}^{(0)} } \rangle = R(1 + \rho )/4$. It therefore follows that the energies split into $E_{0n}^{(0)} \pm \mathcal{E}R(1 + \rho )/4$ providing a gap of $\mathcal{E}R(1 + \rho )/2$. If $\rho \approx 1$, this result agrees with previous exact analyses for one-dimensional rings, for which only the angular degree of freedom remains and the full problem is in the form of a Mathieu equation

$$\left\{ {\frac{1}{{2R^{2} }}\left( { - i\frac{\partial }{\partial \theta } + L} \right)^{2} + \mathcal{E}R\cos \theta } \right\}\varphi_{n} \left( \theta \right) = E_{n} \varphi_{n} \left( \theta \right), $$

(14)

with periodic boundary condition $\varphi_{n} \left( {\theta + 2\pi } \right) = \varphi_{n} \left( \theta \right)$. This problem is perfectly equivalent to the electronic band structure problem in a one-dimensional sinusoidal potential with L playing the role of Bloch momentum. Thus, the lifted degeneracy at $L = 1/2$ is analogous to the band gap created by a periodic potential at the Brillouin zone boundary [26]. The eigenstates of Eq. (14) are of the form $\varphi_{n} \left( \theta \right) = \exp \left( { - iL\theta } \right)\left\{ {A{\text{ce}}_{2L} \left( {\tfrac{1}{2}\theta ,4\mathcal{E}R^{3} } \right) + B{\text{se}}_{2L} \left( {\tfrac{1}{2}\theta ,4\mathcal{E}R^{3} } \right)} \right\}$, where ${\text{ce}}_{2L}$ and ${\text{se}}_{2L}$ are Mathieu functions with characteristic exponent $2L$. The associated energy is $E_{n} = a_{2L} \left( {4\mathcal{E}R^{3} } \right)/\left( {8R^{2} } \right)$ with $a_{2L}$ the characteristic value.

In Fig. 5, we compare numerical energy eigenvalues in vanishing and finite field $\mathcal{E}R^{3} = 0.1$. The numerical values are found from expansion in unperturbed eigenstates with $l \in \left[ { - 20,20} \right]$ and $n \in \left[ {1,20} \right]$. Also, analytical Mathieu equation results are included for thin rings. As expected, the degeneracy is lifted by the finite field, confirming that the diverging perturbative polarizability is a result of an invalid treatment of the electric field in the vicinity of $L = 1/2$. The gap $\mathcal{E}R\left( {1 + \rho } \right)/2$ at $L = 1/2$ leads to a finite polarizability of $\alpha \left( {\tfrac{1}{2}\Phi_{0} ,0} \right) \approx \left( {1 + \rho } \right)R/\left( {4\mathcal{E}} \right)$. Accordingly, the actual polarizability at $L = 1/2$ remains significantly enhanced compared to $\alpha \left( {0,0} \right)$ provided $\mathcal{E}R^{3} \ll 1$. In Fig. 4, numerical results for $\mathcal{E}R^{3} = 0.05$ are included to demonstrate this fact.

Fig. 5

Ground and first excited state energy (relative to $E_{1} \left( 0 \right)$) as a function of flux for rings with various $\rho = R_{{{\text{inner}}}} /R_{{{\text{outer}}}}$. Solid and dashed lines are numerical solutions in finite and vanishing fields, respectively. Also, circles correspond to Mathieu equation solutions for $\rho = 1$

4 Summary

In the present work, we have analyzed a circular nanoring with arbitrary inner and outer radii threaded by an Aharonov–Bohm (AB) magnetic flux. An in-plane electric field polarizes the ring, and the dipole polarizability is examined as a probe of AB effects. By following the Dalgarno–Lewis approach, we derive an analytic expression for the polarizability. This compact closed-form expression is valid for arbitrary AB flux, optical frequency and width of the nanoring. A hallmark of AB effects is the degeneracy between neighboring angular momentum eigenstates at half-integer AB flux. As the transition between such states is dipole allowed, a significant enhancement of the static dipole polarizability near half-integer flux is anticipated. In fact, the present work reveals a general reduction in the polarizability by finite-width effects, yet in all cases, a divergence is observed at half-integer flux. A more rigorous approach treating both magnetic and electric fields non-perturbatively leads to a finite but large response.

Appendix: Bessel product integrals

The literature on indefinite Bessel function integrals is scarce and limited to integer orders, see Ref. [27]. We therefore include the required results allowing for arbitrary order here. In the static case, the integrals encountered in the main text can all be reduced to combinations of the following indefinite Bessel product integrals with $Z_{l} ,Z_{l}^{\prime } \in \left\{ {J_{l} \left( x \right),Y_{l} \left( x \right)} \right\}$:

$$ \int {Z_{l} Z_{{l + 1}}^{\prime } x{\text{d}}x} = \frac{x}{2}\left\{ {xZ_{l} Z_{l}^{\prime } + xZ_{{l + 1}} Z_{{l + 1}}^{\prime } - 2lZ_{{l + 1}} Z_{l}^{\prime } } \right\}. $$

(15)

$$ \int {Z_{l} Z_{{l + 1}}^{\prime } x^{2} {\text{d}}x} = \frac{x}{4}\left\{ {2xlZ_{l} Z_{l}^{\prime } + 2x(l + 1)Z_{{l + 1}} Z_{{l + 1}}^{\prime } + [x^{2} - 4l(l + 1)]Z_{l} Z_{{l + 1}}^{\prime } - x^{2} Z_{{l + 1}} Z_{l}^{\prime } } \right\}. $$

(16)

$$ \int {Z_{l} Z_{l}^{\prime } x^{3} {\text{d}}x} = \frac{x}{6}\left\{ {x\left[ {2\left( {l - 1} \right) + x^{2} } \right]Z_{l} Z_{l}^{\prime } + x\left[ {2\left( {l^{2} - 1} \right) + x^{2} } \right]Z_{{l + 1}} Z_{{l + 1}}^{\prime } \left. { - \left( {l - 1} \right)\left[ {2l(l + 1) + x^{2} } \right]\left( {Z_{l} Z_{{l + 1}}^{\prime } + Z_{{l + 1}} Z_{l}^{\prime } } \right)} \right\}.} \right. $$

(17)

$$ \begin{aligned} \int {Z_{l} Z_{{l + 1}}^{\prime } x^{4} {\text{d}}x} & = \frac{x}{6}\left\{ {x(l - 1)[2l(l + 2) + x^{2} ]Z_{l} Z_{l}^{\prime } + x(l + 2)[2(l^{2} - 1) + x^{2} ]Z_{{l + 1}} Z_{{l + 1}}^{\prime } } \right. \\ & \quad \left. { + \left\{ {[2 - l(l + 1)][4l(l + 1) + x^{2} ] + \tfrac{3}{4}x^{4} } \right\}Z_{l} Z_{{l + 1}}^{\prime } - x^{2} [l(l + 1) - 2 + \tfrac{3}{4}x^{2} ]Z_{{l + 1}} Z_{l}^{\prime } } \right\}. \\ \end{aligned} $$

(18)

Integration constants are omitted. The dynamic case requires indefinite Bessel product integrals with different arguments $Z_{l} \in \left\{ {J_{l} \left( {ax} \right),Y_{l} \left( {ax} \right)} \right\}$ and $Z^{\prime}_{l} \in \left\{ {J_{l} \left( {bx} \right),Y_{l} \left( {bx} \right)} \right\}$:

$$ \int {Z_{l} Z^{\prime}_{l + 1} x^{2} {\text{d}}x = x^{2} \frac{{bZ_{l} Z^{\prime}_{l} + aZ_{l + 1} Z^{\prime}_{l + 1} }}{{a^{2} - b^{2} }} + 2x\frac{{\left[ {\left( {1 + l} \right)b^{2} - la^{2} } \right]Z_{l} Z^{\prime}_{l + 1} - abZ_{l + 1} Z^{\prime}_{l} }}{{\left( {a^{2} - b^{2} } \right)^{2} }}.} $$

(19)

Additionally, the recursion relation

$$ Z_{l} \left( x \right) = \frac{{2\left( {l + 1} \right)}}{x}Z_{l + 1} \left( x \right) - Z_{l + 2} \left( x \right), $$

(20)

and Wronskian

$$ Y_{l} \left( x \right)J_{l + 1} \left( x \right) - J_{l} \left( x \right)Y_{l + 1} \left( x \right) = \frac{2}{\pi x} $$

(21)

are useful in verifying the results of the main text.