Skip to main content
SpringerLink
Log in

Impact of thermal radiation on stretching sheet: a numerical approach using new similarity transformations

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

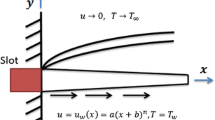
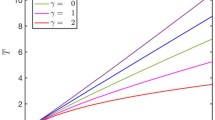
The main objective of this article is to apply novel similarity transformations, which we have developed ourselves. The similarity method holds great potential for solving sets of partial differential equations. However, previous studies on stretching sheets only considered nondimensional similarity variables with respect to a single independent variable, leading to certain inaccuracies. To address this, we have derived a novel set of similarity transformations that encompass all the independent variables used in the analyzed equations. This approach aims to enhance the accuracy of results significantly. The results of this investigation were contrasted with those from past works. It became evident that the previous studies, which relied on a similarity variable based on a single independent variable, contained several inaccuracies. Therefore, we devised a new set of similarity transformations to overcome this limitation. For numerical results, we employed the shooting technique along with Runge–Kutta–Fehlberg’s 4th–5th method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data Availability Statement

This manuscript has no associated data or the data will not be deposited. [Authors’ comment: Not applicable.]

References

  1. A. Acrivos, M.J. Shah, E. Petersen, E: momentum and heat transfer in laminar boundary-layer flows of non?Newtonian fluids past external surfaces. AIChE J. 6(2), 312–317 (1960)

    Article  ADS  Google Scholar 

  2. B.C. Sakiadis, Boundary-layer behavior on: Continuous solid surfaces Boundary?layer equations for two? Dimensional and axisymmetric flow. AIChE J. 7(1), 26–28 (1961)

    Article  ADS  Google Scholar 

  3. F.K. Tsou, E.M. Sparrow, R. Goldstein, J: flow and heat transfer in the boundary layer on a continuously moving surface. Int. J. Heat Mass Transf. 10(2), 219–235 (1967)

    Article  Google Scholar 

  4. P.S. Gupta, A. Gupta, S: heat and mass transfer on a stretching sheet with suction or blowing. Can. J. Chem. Eng. 55(6), 744–746 (1977)

    Article  Google Scholar 

  5. W.A. Khan, Pop, I: boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 53(11–12), 2477–2483 (2010)

    Article  Google Scholar 

  6. K. Bhattacharyya, G. Layek, C: effects of suction/blowing on steady boundary layer stagnation-point flow and heat transfer towards a shrinking sheet with thermal radiation. Int. J. Heat Mass Transf. 54(1–3), 302–307 (2011)

    Article  Google Scholar 

  7. N.S. Akbar, T. Hayat, S. Nadeem, S. Obaidat, The peristaltic flow of a tangent hyperbolic fluid in an inclined asymmetric channel with slip and heat transfer. Prog. Comput. Fluid Dyn. Int. J. 12(5), 363–374 (2012)

    Article  Google Scholar 

  8. Z. Ullah, G. Zaman, Lie group analysis of magnetohydrodynamic tangent hyperbolic fluid flow towards a stretching sheet with slip conditions. Heliyon 3(11), e00443 (2017)

    Article  Google Scholar 

  9. S. Zeb, S. Khan, Z. Ullah, , M. Yousaf, I. Khan, N. Alshammari, N.N. Hamadneh, Lie group analysis of double-diffusive MHD tangent hyperbolic fluid flow over a stretching sheet. Math. Prob. Eng., 2022 (2022)

  10. M. Pakdemirli, E. Suhubi, S: Similarity solutions of boundary layer equations for second-order fluids. Int. J. Eng. Sci. 30(5), 611–629 (1992)

    Article  MathSciNet  Google Scholar 

  11. G. Bognár, Similarity solution of boundary layer flows for non-Newtonian fluids. Int. J. Nonlinear Sci. Numer. Simul. 10(11–12), 1555–1566 (2009)

    Article  Google Scholar 

  12. V.S. Patil, N.S. Patil, M. Timol, G: A remark on similarity analysis of boundary layer equations of a class of non-Newtonian fluids. Int. J. Non-Linear Mech. 71, 127–131 (2015)

    Article  ADS  Google Scholar 

  13. G.W. Bluman, J.D. Cole, Similarity methods for differential equations, vol. 13 (Springer Science & Business Media, Berlin, 2012)

    Google Scholar 

  14. M. Pakdemirli, M. Yurusoy, Similarity transformations for partial differential equations. SIAM Rev. 40(1), 96–101 (1998)

    Article  ADS  MathSciNet  Google Scholar 

  15. M. Qasim, Z.H. Khan, R.J. Lopez, W. Khan, A: Heat and mass transfer in a nanofluid thin film over an unsteady stretching sheet using Buongiorno?s model. Eur. Phys. J. Plus 131, 1–11 (2016)

    Article  Google Scholar 

  16. G.K. Ramesh, B.J. Gireesha, T. Hayat, A. Alsaedi, Stagnation point flow of Maxwell fluid towards a permeable surface in the presence of nanoparticles. Alex. Eng. J. 55(2), 857–865 (2016)

    Article  Google Scholar 

  17. V. Aliakbar, A. Alizadeh-Pahlavan, K. Sadeghy, The influence of thermal radiation on MHD flow of Maxwellian fluids above stretching sheets. Commun. Nonlinear Sci. Numer. Simul. 14(3), 779–794 (2009)

    Article  ADS  Google Scholar 

  18. D. Pal, G. Mandal, Thermal radiation and MHD effects on boundary layer flow of micropolar nanofluid past a stretching sheet with non-uniform heat source/sink. Int. J. Mech. Sci. 126, 308–318 (2017)

    Article  Google Scholar 

  19. S. Manjunatha, B. Gireesha, J: effects of variable viscosity and thermal conductivity on MHD flow and heat transfer of a dusty fluid. Ain Shams Eng. J. 7(1), 505–515 (2016)

    Article  Google Scholar 

  20. K.G. Kumar, B.J. Gireesha, M.R. Krishanamurthy, N. Rudraswamy, G: an unsteady squeezed flow of a tangent hyperbolic fluid over a sensor surface in the presence of variable thermal conductivity. Results Phys. 7, 3031–3036 (2017)

    Article  ADS  Google Scholar 

  21. M.M. Bhatti, M. Rashidi, M: Effects of thermo-diffusion and thermal radiation on Williamson nanofluid over a porous shrinking/stretching sheet. J. Mol. Liq. 221, 567–573 (2016)

    Article  Google Scholar 

  22. H. Sithole, H. Mondal, P. Sibanda, Entropy generation in a second grade magnetohydrodynamic nanofluid flow over a convectively heated stretching sheet with nonlinear thermal radiation and viscous dissipation. Results Phys. 9, 1077–1085 (2018)

    Article  ADS  Google Scholar 

  23. J. Raza, Thermal radiation and slip effects on magnetohydrodynamic (MHD) stagnation point flow of Casson fluid over a convective stretching sheet. Propuls. Power Res. 8(2), 138–146 (2019)

    Article  Google Scholar 

  24. H. Waqas, M. Fida, D. Liu, U. Manzoor, T. Muhammad, Numerical simulation of entropy generation for nanofluid with the consequences of thermal radiation and Cattaneo-Christov heat flux model. Int. Commun. Heat Mass Transf. 137, 106293 (2022)

    Article  Google Scholar 

  25. M. Ferdows, M.J. Uddin, A. Afify, A: scaling group transformation for MHD boundary layer free convective heat and mass transfer flow past a convectively heated nonlinear radiating stretching sheet. Int. J. Heat Mass Transf. 56(1–2), 181–187 (2013)

    Article  Google Scholar 

  26. M. Khan, Flow and heat transfer to modified second-grade fluid over a non-linear stretching sheet. AIP Adv. 5(8), 087157 (2015)

    Article  ADS  Google Scholar 

  27. M. Waqas, M. Farooq, M.I. Khan, A. Alsaedi, T. Hayat, Magnetohydrodynamic (MHD) mixed convection flow of micropolar liquid due to nonlinear stretched sheet with convective condition. Int. J. Heat Mass Transf. 102, 766–772 (2016)

    Article  Google Scholar 

  28. B.C. Prasannakumara, B.J. Gireesha, M.R. Krishnamurthy, K. Kumar, G: MHD flow and nonlinear radiative heat transfer of Sisko nanofluid over a nonlinear stretching sheet. Inf. Med. Unlocked 9, 123–132 (2017)

    Article  Google Scholar 

  29. N.H. Abd Rahman, N. Bachok, H. Rosali, MHD stagnation point flow over a nonlinear stretching/shrinking sheet in nanofluids. J. Adv. Res. Fluid Mech. Thermal Sci. 76(3), 139–152 (2020)

    Article  Google Scholar 

  30. T.V. Laxmi, B. Shankar, Effect of nonlinear thermal radiation on boundary layer flow of viscous fluid over a nonlinear stretching sheet with injection/suction. J. Appl. Math. Phys. 4(2), 307–319 (2016)

    Article  Google Scholar 

  31. A. Shahzad, J. Ahmed, M. Khan, On heat transfer analysis of the axisymmetric flow of viscous fluid over a nonlinear radially stretching sheet. Alex. Eng. J. 55(3), 2423–2429 (2016)

    Article  Google Scholar 

  32. M.R. Krishnamurthy, B.J. Gireesha, B.C. Prasannakumara, R.S. Gorla, R: Thermal radiation and chemical reaction effects on boundary layer slip flow and melting heat transfer of nanofluid induced by a nonlinear stretching sheet. Nonlinear Eng. 5(3), 147–159 (2016)

    Article  ADS  Google Scholar 

  33. T. Hayat, R.S. Saif, R. Ellahi, T. Muhammad, B. Ahmad, Numerical study of boundary-layer flow due to a nonlinear curved stretching sheet with convective heat and mass conditions. Results Phys. 7, 2601–2606 (2017)

    Article  ADS  Google Scholar 

  34. K.G. Kumar, N.G. Rudraswamy, B.J. Gireesha, S. Manjunatha, Non-linear thermal radiation effect on Williamson fluid with particle-liquid suspension past a stretching surface. Results in Phys. 7, 3196–3202 (2017)

    Article  ADS  Google Scholar 

  35. Y.B. Kho, A. Hussanan, N.M. Sarif, Z. Ismail, M.Z. Salleh, Thermal radiation effects on MHD with flow heat and mass transfer in Casson nanofluid over a stretching sheet. In MATEC Web of Conferences (Vol. 150, p. 06036). EDP Sciences (2018)

  36. A.K. Hakeem, M. Govindaraju, B. Ganga, Influence of inclined Lorentz forces on entropy generation analysis for viscoelastic fluid over a stretching sheet with nonlinear thermal radiation and heat source/sink. J. Heat Mass Transf. Res. 6(1), 1–10 (2019)

    Google Scholar 

  37. S.S. Ghadikolaei, K. Hosseinzadeh, D.D. Ganji, B. Jafari, Nonlinear thermal radiation effect on magneto Casson nanofluid flow with Joule heating effect over an inclined porous stretching sheet. Case stud. Thermal Eng. 12, 176–187 (2018)

    Article  Google Scholar 

  38. A.B. Jafar, S. Shafie, I. Ullah, R. Safdar, W. Jamshed, A.A. Pasha, M.R. Eid, Mixed convection flow of an electrically conducting viscoelastic fluid past a vertical nonlinearly stretching sheet. Sci. Rep. 12(1), 14679 (2022)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

The authors are grateful to the department of science and technology of the Government of India for financing as support of the DST-FIST initiative for Higher education institutions (Grant No. SR/FST/MS-I/2018/23(C)).

Author information

Author notes

  1. Sushma, B. J. Gireesha, and C. G. Pavithra have contributed equally to this work.

Authors and Affiliations

  1. Department of PG Studies and Research in Mathematics, Kuvempu University, Shankaraghatta, Shivamogga, Karnataka, 577451, India

    Sushma, B. J. Gireesha & C. G. Pavithra

Authors
  1. Sushma
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. B. J. Gireesha
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. C. G. Pavithra
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Sushma and C.G. Pavitra were contributed to conceptualization, methodology, software, writing original draft. B.J. Gireesha was contributed to conceptualization, methodology, software, writing—review and draft, supervision.

Corresponding author

Correspondence to B. J. Gireesha.

Ethics declarations

Conflict of interest

There are no conflicting priorities among the authors of this publication.

Ethics approval

Not applicable.

Consent to participate

Not applicable.

Consent for publication

Not applicable.

Code availability

Not applicable.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sushma, Gireesha, B.J. & Pavithra, C.G. Impact of thermal radiation on stretching sheet: a numerical approach using new similarity transformations. Eur. Phys. J. Plus 139, 98 (2024). https://doi.org/10.1140/epjp/s13360-024-04876-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-024-04876-y

Search

Navigation