Skip to main content

Advertisement

SpringerLink
Log in

Analysis of an age-structured HIV infection model with cell-to-cell transmission

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

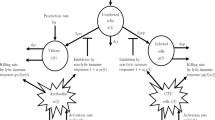
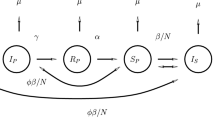
Though cell-to-cell transmission cannot be overlooked in HIV infection, many existing studies have only focused on the cell-free infection. Moreover, the infection rate is an important factor affecting viral transmission. Considering general incidence rates and latently infected cells, we develop an age-structured model with the two transmission modes. The expression of the basic reproduction number is derived. It turns out that the existence and local stability of equilibria is determined by the basic reproduction number. Before establishing the global dynamical behavior, we prove the existence of compact global attractors and uniform persistence. Then, by using the fluctuation lemma and Lyapunov functionals, a threshold dynamics is obtained. Saturated incidence rates are selected to simulate the relationship between latently infected cells and viruses, as well as the role of age-dependent parameters in infection.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Data Availability Statement

No data are associated in the manuscript.

References

  1. K. Manoj, A. Syed, Global dynamics of an age-structured model for HIV viral dynamics with latently infected T cells. Math. Comput. Simul. 198, 237–252 (2022)

    Article  MathSciNet  Google Scholar 

  2. J.H. Xu, Y. Geng, Y.C. Zhou, Global dynamics for an age-structured HIV virus infection model with cellular infection and antiretroviral therapy. Appl. Math. Comput. 305, 62–83 (2017)

    MathSciNet  Google Scholar 

  3. A. Ishaku, A.M. Gazali, S.A. Abdullahi et al., Analysis and optimal control of an HIV model based on CD4 count. J. Math. Biol. 81, 209–241 (2020)

    Article  MathSciNet  Google Scholar 

  4. A.-H. Abdel-Aty, M.M.A. Khater, H. Dutta et al., Computational solutions of the HIV-1 infection of CD4+T-cells fractional mathematical model that causes acquired immunodeficiency syndrome (AIDS) with the effect of antiviral drug therapy. Chaos. Soliton. Fract. 139, 110092 (2020)

    Article  MathSciNet  Google Scholar 

  5. WHO, HIV/AIDS, (2023). https://www.who.int/news-room/fact-sheets/detail/hiv-aids

  6. D.X. Yan, X.L. Fu, Analysis of an age-structured HIV infection model with logistic target-cell growth and antiretroviral therapy. IMA J. Appl. Math. 83(6), 1037–1065 (2018)

    MathSciNet  Google Scholar 

  7. N. Tarfulea, Drug therapy model with time delays for HIV infection with virus-to-cell and cell-to-cell transmissions. J. Appl. Math. Comput. 59, 677–691 (2019)

    Article  MathSciNet  Google Scholar 

  8. P. Aavani, L.J.S. Allen, The role of CD4+ T cells in immune system activation and viral reproduction in a simple model for HIV infection. Appl. Math. Model. 75, 210–222 (2019)

    Article  MathSciNet  Google Scholar 

  9. X. Wang, X.Y. Song, S.Y. Tang et al., Dynamics of an HIV model with multiple infection stages and treatment with different drug classes. Bull. Math. Biol. 78(2), 322–349 (2016)

    Article  MathSciNet  Google Scholar 

  10. X. Wang, Y.J. Lou, X.Y. Song, Age-structured within-host HIV dynamics with multiple target cells. Stud. Appl. Math. 138(1), 43–76 (2017)

    Article  MathSciNet  Google Scholar 

  11. Y. Gao, J.L. Wang, Threshold dynamics of a delayed nonlocal reaction–diffusion HIV infection model with both cell-free and cell-to-cell transmissions. J. Math. Anal. Appl. 488(1), 124047 (2020)

    Article  MathSciNet  Google Scholar 

  12. X.Q. Xie, J.L. Ma, P. van den Driessche, Backward bifurcation in within-host HIV models. Math. Biosci. 335, 108569 (2021)

    Article  MathSciNet  Google Scholar 

  13. M. Goyal, H.M. Baskonus, A. Prakash, Regarding new positive, bounded and convergent numerical solution of nonlinear time fractional HIV/AIDS transmission model. Chaos. Soliton. Fract. 139, 110096 (2020)

    Article  MathSciNet  Google Scholar 

  14. Y. Yang, L. Zou, S.G. Ruan, Global dynamics of a delayed within-host viral infection model with both virus-to-cell and cell-to-cell transmissions. Math. Biosci. 270, 183–191 (2015)

    Article  MathSciNet  Google Scholar 

  15. H.M. Doekes, C. Fraser, K.A. Lythgoe, Effect of the latent reservoir on the evolution of HIV at the within- and between-host levels. Plos. Comput. Biol. 13(1), e1005228 (2017)

    Article  ADS  Google Scholar 

  16. A.M. Elaiw, A.D. Al Agha, S.A. Azoz et al., Global analysis of within-host SARS-CoV-2/HIV coinfection model with latency. Eur. Phys. J. Plus. 137, 174 (2022)

    Article  Google Scholar 

  17. X. Wang, Y. Zhang, X.Y. Song, An age-structured epidemic model with waning immunity and general nonlinear incidence rate. Int. J. Biomath. 11(5), 1850069 (2018)

    Article  MathSciNet  Google Scholar 

  18. L. Shi, L. Wang, L. Zhu et al., Dynamics of an infection-age HIV diffusive model with latent infected cell and Beddington–DeAngelis infection incidence. Eur. Phys. J. Plus. 137, 212 (2022)

    Article  Google Scholar 

  19. X. Wang, Y.M. Chen, M. Martcheva et al., Asymptotic analysis of a vector-borne disease model with the age of infection. J. Biol. Dyn. 14(1), 332–367 (2020)

    Article  MathSciNet  Google Scholar 

  20. X.M. Feng, S.G. Ruan, T.Z. Teng et al., Stability and backward bifurcation in a malaria transmission model with applications to the control of malaria in China. Math. Biosci. 266, 52–64 (2015)

    Article  MathSciNet  Google Scholar 

  21. X. Wang, Y.M. Chen, X.Y. Song, Global dynamics of a cholera model with age structures and multiple transmission modes. Int. J. Biomath. 12(5), 1950051 (2019)

    Article  MathSciNet  Google Scholar 

  22. J.Z. Lin, R. Xu, X.H. Tian, Global dynamics of an age-structured cholera model with both human-to-human and environment-to-human transmissions and saturation incidence. Appl. Math. Model. 63, 688–708 (2018)

    Article  MathSciNet  Google Scholar 

  23. X. Wang, Y.M. Chen, S.Q. Liu, Global dynamics of a vector-borne disease model with infection ages and general incidence rates. Comput. Appl. Math. 37, 4055–4080 (2018)

    Article  MathSciNet  Google Scholar 

  24. L.M. Agosto, P.D. Uchil, W. Mothes, HIV cell-to-cell transmission: effects on pathogenesis and antiretroviral therapy. Trends Microbiol. 23(5), 289–295 (2015)

    Article  Google Scholar 

  25. A. Alshorman, C. Samarasinghe, W.L. Lu et al., An HIV model with age-structured latently infected cells. J. Biol. Dyn. 11(sup1), 192–215 (2017)

    Article  MathSciNet  Google Scholar 

  26. J.L. Wang, J.Y. Lang, X.F. Zou, Analysis of an age structured HIV infection model with virus-to-cell infection and cell-to-cell transmission. Nonlinear. Anal. Real 34, 75–96 (2017)

    Article  MathSciNet  Google Scholar 

  27. J.N. Blankson, D. Persaud, R.F. Siliciano, The challenge of viral reservoirs in HIV-1 infection. Annu. Rev. Med. 53(1), 557–593 (2002)

    Article  Google Scholar 

  28. C.Y. Qin, X. Wang, L.B. Rong, An age-structured model of HIV latent infection with two transmission routes: analysis and optimal control. Complexity 2020, 1890320 (2020). https://doi.org/10.1155/2020/1890320

    Article  Google Scholar 

  29. C.J. Browne, S.S. Pilyugin, Global analysis of age-structured within-host virus model. Discrete. Cont. Dyn B. 18(8), 1999–2017 (2013)

    MathSciNet  Google Scholar 

  30. P. Magal, Compact attractors for time periodic age-structured population models. Electron. J. Differ. Equ. 65, 1–35 (2001)

    MathSciNet  Google Scholar 

  31. M. Martcheva, H.R. Thieme, Progression age enhanced backward bifurcation in an epidemic model with super-infection. J. Math. Biol. 46(5), 385–424 (2003)

    Article  MathSciNet  Google Scholar 

  32. W.M. Hirsch, H. Hanisch, J.P. Gabriel, Differential equation models of some parasitic infections: methods for the study of asymptotic behavior. Commun. Pur. Appl. Math. 38(6), 733–753 (1985)

    Article  MathSciNet  Google Scholar 

  33. S. Bentout, Y.M. Chen, S. Djilali, Global dynamics of an SEIR model with two age structures and a nonlinear incidence. Acta. Appl. Math. 171(1), 7 (2021). https://doi.org/10.1007/s10440-020-00369-z

    Article  MathSciNet  Google Scholar 

  34. H.L. Smith, H.R. Thieme, Dynamical Systems and Population Persistence (American Mathematical Society, Providence, 2011), pp.126–379

    Google Scholar 

  35. A. Alshorman, X. Wang, M. Joseph-Meyer et al., Analysis of HIV models with two time delays. J. Biol. Dyn. 11(sup1), 40–64 (2017)

    Article  MathSciNet  Google Scholar 

  36. X. Wang, S.Y. Tang, X.Y. Song et al., Mathematical analysis of an HIV latent infection model including both virus-to-cell infection and cell-to-cell transmission. J. Biol. Dyn. 11(sup2), 455–483 (2017)

    Article  MathSciNet  Google Scholar 

  37. X. Wang, Y.M. Chen, S.Q. Liu, Dynamics of an age-structured host-vector model for malaria transmission. Math. Method. Appl. Sci. 41(5), 1966–1987 (2018)

    Article  ADS  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work is supported partially by the National Natural Science Foundation of China (No. 12171413), the Natural Science Foundation of Henan Province (222300420016), and the Program for Science and Technology Innovation Teams in Henan (21IRTSTHN014), and the Scientific Research Foundation of Graduate School of Xinyang Normal University (No. 2022KYJJ010).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Xinyang Normal University, Xinyang, 464000, China

    Jie Li & Xia Wang

  2. Department of Mathematics, Wilfrid Laurier University, Waterloo, N2L 3C5, Canada

    Yuming Chen

Authors
  1. Jie Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xia Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yuming Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xia Wang.

Ethics declarations

Conflicts of interest

There are no financial or interpersonal conflicts in our paper.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, J., Wang, X. & Chen, Y. Analysis of an age-structured HIV infection model with cell-to-cell transmission. Eur. Phys. J. Plus 139, 78 (2024). https://doi.org/10.1140/epjp/s13360-024-04873-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-024-04873-1

Search

Navigation