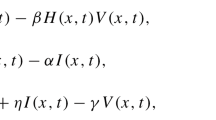Skip to main content
SpringerLink
Log in

Stability analysis of spatiotemporal reaction–diffusion mathematical model incorporating the varicella virus transmission

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

We introduce an epidemic disease reaction–diffusion model to study the transmission of the varicella-zoster virus in both space and time. More precisely, we present a system of partial differential equations with the Neumann boundary conditions (NBC) concerned to model the evolution of the virus. Firstly, the wellposedness results of the model are studied using the semigroup theory. Then, the boundedness of the solutions is also derived. Further, the basic reproduction number (BRN) for the proposed model is determined using the eigenvalue problem. Moreover, asymptotic profiles of the equilibrium points of the susceptible and infected compartments of the model are investigated. Finally, the advantage of the spatiotemporal model and the above theoretical results are validated with numerical experiments.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data Availability Statement

No data associated with this manuscript.

References

  1. Z. Ahmad, G. Bonanomi, D. di Serafino, F. Giannino, Transmission dynamics and sensitivity analysis of pine wilt disease with asymptomatic carriers via fractal-fractional differential operator of Mittag-Leffler kernel. Appl. Numer. Math. 185, 446–465 (2023)

    Article  MathSciNet  Google Scholar 

  2. F. Ayoade, S. Kumar, Varicella zoster (chickenpox), StatPearls (Treasure Island (FL) (2020)

  3. A.W. Blair, W.M. Jamieson, G.H. Smith, Complications and death in chicken-pox. BMJ 2(5468), 981 (1965)

    Article  Google Scholar 

  4. C.E. Rotem, Complications of chicken-pox. BMJ 1(5230), 944 (1961)

    Article  Google Scholar 

  5. A. Suzuki, H. Nishiura, Transmission dynamics of varicella before, during and after the COVID-19 pandemic in Japan: a modelling study. Math. Biosci. Eng. 19(6), 5998–6012 (2022)

    Article  Google Scholar 

  6. M. Wilson, P.J.K. Wilson, Close Encounters of the Microbial Kind: Everything You Need to Know About Common Infections (Springer Nature, Switzerland AG, 2021)

    Book  Google Scholar 

  7. Z. Ali, F. Rabiei, M.M. Rashidi, T. Khodadadi, A fractional-order mathematical model for COVID-19 outbreak with the effect of symptomatic and asymptomatic transmissions. Eur. Phys. J. Plus 137(3), 395 (2022)

    Article  Google Scholar 

  8. N. Bai, R. Xu, Modelling of HIV viral load and 2-LTR dynamics during high active antiretroviral therapy in a heterogeneous environment. Commun. Nonlinear Sci. Numer. Simul. 116, 106874 (2023)

    Article  MathSciNet  Google Scholar 

  9. S. Bera, S. Khajanchi, T.K. Roy, Stability analysis of fuzzy HTLV-I infection model: a dynamic approach. J. Appl. Math. Comput. 69(1), 171–199 (2023)

    Article  MathSciNet  Google Scholar 

  10. A. Debbouche, J.J. Nieto, D.F.M. Torres, Focus point: cancer and HIV/AIDS dynamics-from optimality to modelling. Eur. Phys. J. Plus 136(2), 165 (2021)

    Article  Google Scholar 

  11. J. Manimaran, L. Shangerganesh, A. Debbouche, J.C. Cortés, A time-fractional HIV infection model with nonlinear diffusion. Results Phys. 25, 104293 (2021)

    Article  Google Scholar 

  12. G. Nazir, K. Shah, A. Debbouche, R.A. Khan, Study of HIV mathematical model under nonsingular kernel type derivative of fractional order. Chaos Solitons Fractals 139, 110095 (2020)

    Article  MathSciNet  Google Scholar 

  13. F. Ndaïrou, I. Area, J.J. Nieto, D.F.M. Torres, Mathematical modeling of COVID-19 transmission dynamics with a case study of Wuhan. Chaos Solitons Fractals 135, 109846 (2020)

    Article  MathSciNet  Google Scholar 

  14. A. Olivares, E. Staffetti, Robust optimal control of compartmental models in epidemiology: application to the COVID-19 pandemic. Commun. Nonlinear Sci. Numer. Simul. 111, 106509 (2022)

    Article  MathSciNet  Google Scholar 

  15. S. Tyagi, S.C. Martha, S. Abbas, A. Debbouche, Mathematical modeling and analysis for controlling the spread of infectious diseases. Chaos Solitons Fractals 144, 110707 (2021)

    Article  MathSciNet  Google Scholar 

  16. B.G. Wang, Z.C. Wang, Y. Wu, Y. Xiong, J. Zhang, Z. Ma, A mathematical model reveals the influence of NPIs and vaccination on SARS-CoV-2 Omicron Variant. Nonlinear Dyn. 111(4), 3937–3952 (2023)

    Article  Google Scholar 

  17. S. Edward, D. Kuznetsov, S. Mirau, Modeling and stability analysis for a varicella zoster virus model with vaccination. Appl. Comput. Math. 3(4), 150–162 (2014)

    Article  Google Scholar 

  18. A. Elisha, T. Aboiyar, A.R. Kimbir, Mathematical analysis of varicella zoster virus model. Int. J. Discrete Math. 6(2), 23–37 (2021)

    Article  Google Scholar 

  19. S. Qureshi, A. Yusuf, Modeling chickenpox disease with fractional derivatives: from caputo to atangana-baleanu. Chaos Solitons Fractals 122, 111–118 (2019)

    Article  ADS  MathSciNet  Google Scholar 

  20. H.L. Smith, H.R. Thieme, Dynamical Systems and Population Persistence, vol. 118 (American Mathematical Society, Providence, 2011)

    Google Scholar 

  21. F.B. Wang, J. Shi, X. Zou, Dynamics of a host-pathogen system on a bounded spatial domain. Commun. Pure Appl. Anal. 14(6), 2535–2560 (2015)

    Article  MathSciNet  Google Scholar 

  22. V. Capasso, Global solution for a diffusive nonlinear deterministic epidemic model. SIAM J. Appl. Math. 35(2), 274–284 (1978)

    Article  MathSciNet  Google Scholar 

  23. L.J.S. Allen, B.M. Bolker, Y. Lou, A.L. Nevai, Asymptotic profiles of the steady states for an SIS epidemic reaction–diffusion model. Discrete Contin. Dyn. Syst. 21(1), 1–20 (2008)

    Article  MathSciNet  Google Scholar 

  24. F.B. Wang, Y. Huang, X. Zou, Global dynamics of a PDE in-host viral model. Appl. Anal. 93(11), 2312–2329 (2014)

    Article  MathSciNet  Google Scholar 

  25. H.R. Horst, Spectral bound and reproduction number for infinite-dimensional population structure and time heterogeneity. SIAM J. Appl. Math. 70(1), 188–211 (2009)

    Article  MathSciNet  Google Scholar 

  26. P. Magal, X.Q. Zhao, Global attractors and steady states for uniformly persistent dynamical systems. SIAM J. Math. Anal. 37(1), 251–275 (2005)

    Article  MathSciNet  Google Scholar 

  27. H.L. Smith, X.Q. Zhao, Robust persistence for semidynamical systems. Nonlinear Anal. Theory Methods Appl. 47(9), 6169–6179 (2001)

    Article  MathSciNet  Google Scholar 

  28. A. Pazy, Semigroups of Linear Operators and Applications to Partial Differential Equations (Springer-Verlag, New York, 1983)

    Book  Google Scholar 

  29. W. Desch, W. Schappacher, Linearized stability for nonlinear semigroups, Differential Equations in Banach Spaces: Proceedings of a Conference held in Bologna, July 2?5, 1985, Berlin, Heidelberg: Springer Berlin Heidelberg (2006)

  30. H.L. Smith, Monotone dynamical systems: an introduction to the theory of competitive and cooperative systems, No. 41, American Mathematical Society (1995)

  31. R.H. Martin, H.L. Smith, Abstract functional-differential equations and reaction–diffusion systems. Trans. Am. Math. Soc. 321(1), 1–44 (1990)

    MathSciNet  Google Scholar 

  32. P.V. den Driessche, J. Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180(1–2), 29–48 (2002)

    Article  MathSciNet  Google Scholar 

  33. O. Diekmann, J.A.P. Heesterbeek, J.A.J. Metz, On the definition and the computation of the basic reproduction ratio \(R_0\) in models for infectious diseases in heterogeneous populations. J. Math. Biol. 28, 365–382 (1990)

    Article  MathSciNet  Google Scholar 

  34. P. Magal, G.F. Webb, Y. Wu, On the basic reproduction number of reaction–diffusion epidemic models. SIAM J. Appl. Math. 79(1), 284–304 (2019)

    Article  MathSciNet  Google Scholar 

  35. W. Wang, X.Q. Zhao, Basic reproduction numbers for reaction–diffusion epidemic models. SIAM J. Appl. Dyn. Syst. 11(4), 1652–1673 (2012)

    Article  MathSciNet  Google Scholar 

  36. L.C. Evans, Partial Differential Equations, vol. 19 (American Mathematical Society, Providence, 2022)

    Google Scholar 

  37. J. Wang, W. Wu, T. Kuniya, Global threshold analysis on a diffusive host?pathogen model with hyperinfectivity and nonlinear incidence functions. Math. Comput. Simul. 203, 767–802 (2023)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Applied Sciences, National Institute of Technology Goa, Goa, 403 401, India

    S. Hariharan & L. Shangerganesh

  2. Department of Mathematics, Guelma University, 24000, Guelma, Algeria

    A. Debbouche

  3. Department of Mathematics, Peter the Great Saint Petersburg Polytechnic University, Saint Petersburg, Russia, 195251

    V. Antonov

Authors
  1. S. Hariharan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. L. Shangerganesh
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. Debbouche
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. V. Antonov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Debbouche.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hariharan, S., Shangerganesh, L., Debbouche, A. et al. Stability analysis of spatiotemporal reaction–diffusion mathematical model incorporating the varicella virus transmission. Eur. Phys. J. Plus 138, 1123 (2023). https://doi.org/10.1140/epjp/s13360-023-04777-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-023-04777-6

Search

Navigation