Skip to main content
SpringerLink
Log in

Isolating patterns in a reaction-diffusion system with Smith population growth

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

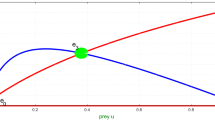
Abstract

The present article concerns itself with the theoretical investigation on an interacting species model system with special emphasis on the species growth followed by Smith and a constant proportion of prey refuge. The prime objective of the study is to provide an adequate mathematical framework in order to carry out a comprehensive analytical investigation of the dynamical complexity between predator and prey species. The proposed model system is not only explored in the perception of diverse local bifurcations in a two-dimensional plane but also of the global bifurcations about coexistence equilibria under specific parametric conditions. For the purpose of validation of all the analytical outcomes together with the applicability of the model concerned, a quantitative sensitivity analysis based on numerical simulation is performed. The evolution of diffusion-driven pattern formation in two-dimensional plane in terms of spot, stripe, labyrinthine, stripe-hole mixture and hole replication as well is patently exhibited. These patterns are all influenced by both the Smith growth principle and prey refuge of the diffusive system. Finally, the influence of model parameters of significance on the dynamics of the proposed model system is, however, not ruled out to depict graphically from the present study.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28

Similar content being viewed by others

Availability of data and materials

This research paper does not fall within the definition of “data sharing” because no code or dataset has been created or examined during the current investigation.

References

  1. https://www.theguardian.com/environment/2020/jan/04/lethal-algae-blooms-an-ecosystem-out-of-balance

  2. E. Shao, Those Seaweed Blobs Headed for Florida? See How Big They Are, The New York Times, ISSN 0362-4331, April 19, (2023)

  3. J.T. Turner, P.A. Tester, Toxic marine phytoplankton zooplankton grazers and pelagic food webs. Limnol. Oceanogr. 425(2), 1203–1213 (1997)

    Article  ADS  Google Scholar 

  4. J. Norberg, D. DeAngelis, Temperature effects on stocks and stability of a phytoplankton-zooplankton model and the dependence on light and nutrients. Ecol. Model. 95(1), 75–86 (1997)

    Article  Google Scholar 

  5. E. Beltrami, T. Carroll, Modeling the role of viral disease in recurrent phytoplankton blooms. J. Math. Biol. 32, 857–863 (1994)

    Article  MATH  Google Scholar 

  6. J. Li, Y. Song, H. Wan, H. Zhu, Dynamical analysis of a toxin-producing phytoplankton-zooplankton model with refuge. Math. Biosci. Eng. 14(2), 529–557 (2017)

    MathSciNet  MATH  Google Scholar 

  7. Y. Lv, Y. Pei, S. Gao, C. Li, H. Zhu, Harvesting of a phytoplankton-zooplankton model. Nonlinear Anal. Real World Appl. 11(5), 3608–3619 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  8. Y. Lv, Y. Pei, S. Gao, C. Li, H. Zhu, Role of toxin and nutrient for the occurrence and termination of plankton bloom-Results drawn from field observations and a mathematical model. Biosystems 90(1), 87–100 (2007)

    Article  Google Scholar 

  9. J. Chattopadhayay, R.R. Sarkar, S. Mandal, Toxin-producing plankton may act as a biological control for planktonic blooms-field study and mathematical modelling. J. Theor. Biol. 215(3), 333–344 (2002)

    Article  ADS  Google Scholar 

  10. E. Granéli, N. Johansson, Effects of the toxic haptophyte Prymnesium parvum on the survival and feeding of a ciliate: the influence of different nutrient conditions. Mar. Ecol. Prog. Ser. 254, 49–56 (2003)

    Article  ADS  Google Scholar 

  11. E. Granéli, N. Johansson, A phytoplankton-toxic phytoplankton-zooplankton model. Ecol. Complex 8(3), 239–248 (2011)

    Article  Google Scholar 

  12. R. Han, G. Mandal, L.N. Guin, S. Chakravarty, Dynamical response of a reaction-diffusion predator-prey system with cooperative hunting and prey refuge. J. Stat. Mech: Theory Exp. 2022(10), 103502 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  13. L.N. Guin, S. Djilali, S. Chakravarty, Cross-diffusion-driven instability in an interacting species model with prey refuge. Chaos, Solitons & Fractals 153, 111501 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  14. J.G. Wang, X.Y. Meng, L. Lv, J. Li, Stability and bifurcation analysis of a Beddington-DeAngelis Prey-Predator model with fear effect, prey refuge and harvesting. Int. J. Bifurcation and Chaos 33(01), 2350013 (2023)

    Article  ADS  MathSciNet  Google Scholar 

  15. L.N. Guin, P.J. Pal, J. Alzahrani, N. Ali, K. Sarkar, S. Djilali, A. Zeb, I. Khan, S.M. Eldin, Influence of Allee effect on the spatiotemporal behaviour of a diffusive predator-prey model with Crowley-Martin type response function. Sci. Rep. 13(1), 4710 (2023)

    Article  ADS  Google Scholar 

  16. D. Xiao, S. Ruan, Global dynamics of a ratio-dependent predator-prey system. J. Math. Biol. 43, 268–290 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  17. W.E.I. Fengying, W. Ke, Economic harvesting model with variable price and cost for population with Smith growth and Cui Lawson growth. Int. J. Biomath. 19(3), 328–336 (2004)

    MathSciNet  Google Scholar 

  18. F.E. Smith, Population dynamics in Daphnia magna and a new model for population growth. Ecology 44(4), 651–663 (1963)

    Article  Google Scholar 

  19. Z. Ma, W. Li, Y. Zhao, W. Wang, H. Zhang, Z. Li, Effects of prey refuges on a predator-prey model with a class of functional responses: the role of refuges. Math. Biosci. 218(2), 73–79 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  20. S. Samaddar, M. Dhar, P. Bhattacharya, Effect of fear on prey-predator dynamics Exploring the role of prey refuge and additional food. Chaos: An Interdisciplinary J. Nonlinear Sci. 30(6), 063129 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  21. J. Ghosh, B. Sahoo, S. Poria, Prey-predator dynamics with prey refuge providing additional food to predator. Chaos, Solitons & Fractals 96, 110–119 (2017)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  22. C. Xiang, J. Huang, H. Wang, Bifurcations in Holling-Tanner model with generalist predator and prey refuge. J. Differential Equ. 343, 495–529 (2023)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  23. R. Han, L.N. Guin, S. Acharya, Complex dynamics in a reaction-cross-diffusion model with refuge depending on predator-prey encounters. Eur. Phys. J. Plus 137(1), 134 (2022)

    Article  Google Scholar 

  24. Z. Wei, F. Chen, Dynamics of a Delayed Predator-Prey Model with Prey Refuge, Allee Effect and Fear Effect. Int. J. Bifurcation and Chaos 33(03), 2350036 (2023)

    Article  ADS  MathSciNet  Google Scholar 

  25. R. Han, L.N. Guin, B. Dai, Consequences of refuge and diffusion in a spatiotemporal predator-prey model. Nonlinear Anal. Real World Appl. 60, 103311 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  26. J. Maynard-Smith, Models in Ecology (Cambridge University Press, Cambridge, 1974)

    MATH  Google Scholar 

  27. M.P. Hassell, The Dynamics of Arthopod Predator-Prey System (Princeton University Press, Princeton, 2020)

    Google Scholar 

  28. J.N. McNair, The effects of refuges on predator-prey interactions: a reconsideration. Theor. Popul. Biol. 29(1), 38–63 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  29. J.B. Collings, Bifurcation and stability analysis of a temperature-dependent mite predator-prey interaction model incorporating a prey refuge. Bull. Math. Biol. 57, 63–76 (1995)

    Article  MATH  Google Scholar 

  30. E. González-Olivares, R. Ramos-Jiliberto, Dynamic consequences of prey refuges in a simple model system: more prey, fewer predators and enhanced stability. Ecol. Model 166(1–2), 135–146 (2003)

    Article  Google Scholar 

  31. Y. Huang, F. Chen, L. Zhong, Stability analysis of a prey-predator model with Holling type III response function incorporating a prey refuge. Appl. Math. Comput. 182(1), 672–683 (2006)

    MathSciNet  MATH  Google Scholar 

  32. P.D.N. Srinivasu, I.L. Gayatri, Influence of prey reserve capacity on predator-prey dynamics. Ecol. Model. 181(2–3), 191–202 (2002)

    Google Scholar 

  33. L.N. Guin, S. Pal, S. Chakravarty, S. Djilali, Pattern dynamics of a reaction-diffusion predator-prey system with both refuge and harvesting. Int. J. Biomath. 14(1), 2050084 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  34. M.M. Mullin, E.F. Stewart, F.J. Fuglister, Ingestion by planktonic grazers as a function of concentration of food 1. Limnol. Oceanogr. 20(2), 259–262 (1975)

    Article  ADS  Google Scholar 

  35. A.M. Turing, The chemical basis of morphogenesis. Philosop. Trans. Royal Series B 237(64), 37–72 (1952)

    MathSciNet  MATH  Google Scholar 

  36. X.Y. Tao, L.H. Zhu, Study of periodic diffusion and time delay induced spatiotemporal patterns in a predator-prey system. Chaos, Solitons & Fractals 150, 111101 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  37. W.S. Burnside, A.W. Panton, The theory of equations: with an introduction to the theory of binary algebraic forms (Dublin University Press Series, Dublin, 1892)

    MATH  Google Scholar 

  38. L. Perko, Differential Equations and Dynamical Systems (Springer, New York, 2001)

    Book  MATH  Google Scholar 

  39. S. Wiggins, Introduction to Applied Nonlinear Dynamical Systems and Chaos (Springer, New York, 2003)

    MATH  Google Scholar 

  40. Y.A. Kuznetsov, Elements of Applied Bifurcation Theory (Springer, New York, 1988)

    Google Scholar 

  41. R.I. Bogdanov, Bifurcation of the limit cycle of a family of plane vector field. Sel. Math. Sov. 4, 373–387 (1981)

    MATH  Google Scholar 

  42. R.I. Bogdanov, Versal deformations of a singular point on the plane in the case of zero eigenvalues. Nonlinear Functional Anal. Appl. 9, 144–145 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  43. F. Takens, Forced Oscillations and Bifurcations Applications of Global Analysis (Institute of Utrecht, Netherlands, 1974)

    Google Scholar 

  44. J.C. Helton, F.J. Davis, J.D. Johnson, A comparison of uncertainty and sensitivity analysis results obtained with random and Latin hypercube sampling. Reliab. Eng. Syst. Saf. 89(3), 305–330 (2005)

    Article  Google Scholar 

  45. N. Chitnis, J.M. Hyman, J.M. Cushing, Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull. Math. Biol. 5, 1272–1296 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  46. M.D. Samsuzzoha, M. Singh, D. Lucy, Uncertainty and sensitivity analysis of the basic reproduction number of a vaccinated epidemic model of influenza. Appl. Math. Model. 37(3), 903–915 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  47. J. Shen, Y.M. Jung, Geometric and stochastic analysis of reaction-diffusion patterns. Int. J. Pure Appl. Math. 19(2), 195–244 (2005)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors thank the learned reviewers and the journal editors for their valuable suggestions and comments, which significantly improved the quality of the paper. The Council of Scientific and Industrial Research (CSIR), Government of India, New Delhi, is gratefully acknowledged by Mr. G. Mandal, for providing financial support in the shape of a Junior Research Fellowship (File No.: 09/0202(16462)/2023-EMR-I Dated 14.03.2023).

Funding

This research has no funding at all.

Author information

Authors and Affiliations

  1. Department of Mathematics, Visva-Bharati, Santiniketan, 731235, India

    Lakshmi Narayan Guin, Sukanya Das, Gourav Mandal, Swagata Dutta & Santabrata Chakravarty

Authors
  1. Lakshmi Narayan Guin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sukanya Das
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Gourav Mandal
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Swagata Dutta
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Santabrata Chakravarty
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

S Chakravarty and LN Guin visualized the presented idea. LN Guin and G Mandal developed the analytical theory and performed numerical simulations. S Das, G Mandal, and S Dutta verified the analytical methods. All authors discussed the simulated outcomes and contributed to the final manuscript.

Corresponding author

Correspondence to Santabrata Chakravarty.

Ethics declarations

Conflict of interest

The authors confirm that the publishing of this paper does not involve any conflicts of interest.

Ethical approval

All the researchers have adhered to the accepted ethical standards of a genuine research study. No animals are harmed during this research study. This research has been conducted by maintaining the balance of bio-diversity and practicing honesty in all professional relationships and endeavours.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Guin, L.N., Das, S., Mandal, G. et al. Isolating patterns in a reaction-diffusion system with Smith population growth. Eur. Phys. J. Plus 138, 829 (2023). https://doi.org/10.1140/epjp/s13360-023-04466-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-023-04466-4

Mathematics Subject Classification

Search

Navigation