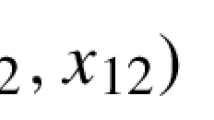Skip to main content
SpringerLink
Log in

Multi-soliton solutions for the two-component modified short pulse equation and its nonlocal reductions via Bäcklund transformations

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

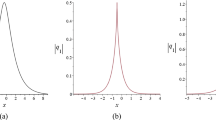
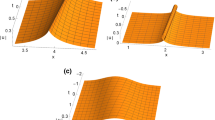
Using the reciprocal transformation and the associated equation, a Bäcklund transformation (BT) involving both independent and dependent variables is constructed and studied for the two-component modified short pulse (2mSP) equation. Through the permutability property, the related nonlinear superposition formula (NSF) and multi-BT are worked out. The multi-soliton solutions of the 2mSP equation are also constructed by means of multi-BT. By reducing the soliton solutions of the 2mSP equation, multi-soliton solutions for the four \({{\mathcal {P}}}{{\mathcal {T}}}\) symmetric nonlocal reductions, which are the real (complex) reverse space-time nonlocal focusing (defocusing) mSP equations, are calculated respectively. In particular, the multi-cuspon-like solutions and multi-breather-like solutions with the influence of nonlocality as well as their interaction are presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21

Similar content being viewed by others

Data Availability Statement

This manuscript has associated data in a data repository [Authors’ comment: All data included in this article are available upon request by contacting the corresponding author.].

References

  1. T. Schäfer, C.E. Wayne, Propagation of ultra-short optical pulses in cubic nonlinear media. Phys. D 196, 90–105 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  2. Y. Chung, C.K.R.T. Jones, T. Schäfer, C.E. Wayne, Ultra-short pulses in linear and nonlinear media. Nonlinearity 18, 1351–1374 (2005)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  3. M.L. Rabelo, On equations which describe pseudospherical surfaces. Stud. Appl. Math. 81, 221–248 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  4. A. Sakovich, S. Sakovich, The short pulse equation is integrable. J. Phys. Soc. Jpn. 74, 239–241 (2005)

    Article  ADS  MATH  Google Scholar 

  5. R. Beals, M. Rabelo, K. Tenenblat, Bäcklund transformations and inverse scattering solutions for some pseudospherical surface equations. Stud. Appl. Math. 81, 125–151 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  6. J.C. Brunelli, The short pulse hierarchy. J. Math. Phys. 46, 123507 (2005)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  7. J.C. Brunelli, The bi-Hamiltonian structure of the short pulse equation. Phys. Lett. A 353, 475–478 (2006)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  8. A. Sakovich, S. Sakovich, Solitary wave solutions of the short pulse equation. J. Phys. A Math. Gen. 39, L361–L367 (2006)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  9. Y. Matsuno, Multiloop soliton and multibreather solutions of the short pulse model equation. J. Phys. Soc. Jpn. 76, 084003 (2007)

    Article  ADS  Google Scholar 

  10. Y. Matsuno, Periodic solutions of the short pulse model equation. J. Math. Phys. 49, 073508 (2008)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  11. S. Liu, L. Wang, W. Liu, D. Qiu, J. He, The determinant representation of an N-fold Darboux transformation for the short pulse equation. J. Nonl. Math. Phys. 24, 183–194 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  12. H. Mao, Q.P. Liu, The short pulse equation: Bäcklund transformations and applications. Stud. Appl. Math. 145, 791–811 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  13. A. Boutet de Monvel, D. Shepelsky, L. Zielinski, The short pulse equation by a Riemann–Hilbert approach. Lett. Math. Phys. 107, 1345–1373 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  14. J. Xu, Long-time asymptotics for the short pulse equation. J. Diff. Equ. 265, 3494–3532 (2018)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  15. S. Sakovich, Transformation and integrability of a generalized short pulse equation. Commnu. Nonlinear Sci. Numer. Simul. 39, 21–28 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  16. B.F. Feng, An integrable coupled short pulse equation. J. Phys. A Math. Theor. 45, 085202 (2012)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  17. Y. Matsuno, Integrable multi-component generalization of a modified short pulse equation. J. Math. Phys. 57, 111507 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  18. B. Guo, N. Liu, A Riemann–Hilbert approach for the modified short pulse equation. Appl. Anal. 98, 1–14 (2018)

    MathSciNet  Google Scholar 

  19. G.Q. Bo, W.G. Zhang, Initial value problem and soliton solutions of the single-cycle short pulse equation via the Riemann–Hilbert approach. J. Phys. Commun. 2, 115004 (2018)

    Article  Google Scholar 

  20. M. Li, Z. Yin, Global existence and local well-posedness of the single-cycle pulse equation. J. Math. Phys. 58, 101515 (2017)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  21. D.V. Kartashov, A.V. Kim, S.A. Skobelev, Soliton structures of a wave field with an arbitrary number of oscillations in nonresonance media. JETP Lett. 78, 276–280 (2003)

    Article  ADS  Google Scholar 

  22. S. Sakovich, Integrability of the vector short pulse equation. J. Phys. Soc. Jpn. 77, 123001 (2008)

    Article  ADS  Google Scholar 

  23. A. Dimakis, F. Muller-Hoissen, Bidifferential calculus approach to AKNS hierarchies and their solutions. SIGMA 6, 055 (2010)

    MathSciNet  MATH  Google Scholar 

  24. M. Pietrzyk, I. Kanattšikov, U. Bandelow, On the propagation of vector ultrashort pulses. J. Nonl. Math. Phys. 15, 162–170 (2008)

    Article  MATH  Google Scholar 

  25. Y. Yao, Y. Zeng, Coupled short pulse hierarchy and its Hamiltonian structure. J. Phys. Soc. Jpn. 80, 064004 (2011)

    Article  ADS  Google Scholar 

  26. Y. Matsuno, A novel multi-component generalization of the short pulse equation and its multisoliton solutions. J. Math. Phys. 52, 123702 (2011)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  27. Zhaqilao, A pair of modified short pulse equations and its two-component system in nonlinear media. Wave Motion 96, 102553 (2020)

  28. C. Lv, D. Qiu, Q.P. Liu, Riemann–Hilbert approach to two-component modified short-pulse system and its nonlocal reductions. Chaos 32, 093120 (2022)

    Article  ADS  MathSciNet  Google Scholar 

  29. C.M. Bender, S. Boettcher, Real spectra in non-Hermitian Hamiltonians having \({\cal{P} }{\cal{T} }\) symmetry. Phys. Rev. Lett. 80, 5243 (1998)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  30. C.M. Bender, \({\cal{P} }{\cal{T} }\) Symmetry (World Scientific, 2019)

    Google Scholar 

  31. M.J. Ablowitz, Z.H. Musslimani, Integrable nonlocal nonlinear Schrödinger equation. Phys. Rev. Lett. 110, 064105 (2013)

    Article  ADS  Google Scholar 

  32. A.K. Sarma, M.A. Miri, Z.H. Musslimani, D.N. Christodoulides, Continuous and discrete Schrödinger systems with parity-time-symmetric nonlinearities. Phys. Rev. E 89, 052918 (2014)

    Article  ADS  Google Scholar 

  33. M.J. Ablowitz, Z.H. Musslimani, Inverse scattering transform for the integrable nonlocal nonlinear Schrödinger equation. Nonlinearity 29, 915–946 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  34. D. Sinha, P.K. Ghosh, Integrable nonlocal vector nonlinear Schrödinger equation with self-induced parity-time-symmetric potential. Phys. Lett. A 381, 124–128 (2017)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  35. M.J. Ablowitz, Z.H. Musslimani, Integrable nonlocal nonlinear equations. Stud. Appl. Math. 139, 7–59 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  36. J.C. Brunelli, Nonlocal short pulse equations. Braz. J. Phys. 48, 421–425 (2018)

    Article  ADS  Google Scholar 

  37. M.J. Ablowitz, X.D. Luo, Z.H. Musslimani, Inverse scattering transform for the nonlocal nonlinear Schrödinger equation with nonzero boundary conditions. J. Math. Phys. 59, 011501 (2018)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  38. M.J. Ablowitz, B.F. Feng, X.D. Luo, Z.H. Musslimani, Reverse space-time nonlocal sine-Gordon/sinh-Gordon equations with nonzero boundary conditions. Stud. Appl. Math. 141, 267–307 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  39. Y. Rybalko, D. Shepelsky, Long-time asymptotics for the integrable nonlocal nonlinear Schrödinger equation. J. Math. Phys. 60, 031504 (2019)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  40. J.L. Ji, Z.N. Zhu, Soliton solutions of an integrable nonlocal modified Korteweg-de Vries equation through inverse scattering transform. J. Math. Anal. Appl. 453, 973–984 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  41. Y. Hanif, H. Sarfraz, U. Saleem, Dynamics of loop soliton solutions of \({\cal{P} }{\cal{T} }\)-symmetric nonlocal short pulse equation. Nonlinear Dyn. 100, 1559 (2020)

    Article  Google Scholar 

  42. G. Zhang, Z. Yan, Inverse scattering transforms and soliton solutions of focusing and defocusing nonlocal mKdV equations with non-zero boundary conditions. Phys. D 402, 132170 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  43. H. Sarfraz, U. Saleem, Symmetry broken and symmetry preserving multi-soliton solutions for nonlocal complex short pulse equation. Chaos Solitons Fractals 130, 109451 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  44. C. Rogers, W.F. Shadwick, Bäcklund Transformations and Their Applications (Academic Press, 1982)

    MATH  Google Scholar 

  45. C. Gu, H. Hu, Z. Zhou, Darboux Transformation in Soliton Theory and Its Geometric Applications (Shanghai Science and Technology Press, 2005)

    Google Scholar 

  46. C. Rogers, W. Schief, Bäcklund and Darboux Transformations-Geoemtry and Modern Applications in Soliton Theory (Cambridge University Press, 2002)

    Book  MATH  Google Scholar 

  47. D. Levi, R. Benguria, Bäcklund transformations and nonlinear differential difference equations. Proc. Natl. Acad. Sci. U.S.A. 77, 5025–5027 (1980)

    Article  ADS  MATH  Google Scholar 

  48. D. Levi, Nonlinear differential difference equations as Bäcklund transformations. J. Phys. A Math. Gen. 14, 1083–1098 (1981)

    Article  ADS  MATH  Google Scholar 

  49. Y.B. Suris, The Problem of Integrable Discretization: Hamiltonian Approach (Birkhäuser, Basel, 2003)

    Book  MATH  Google Scholar 

  50. J. Hietarinta, N. Joshi, F.W. Nijhoff, Discrete Systems and Integrability (Cambriage University Press, 2016)

    Book  MATH  Google Scholar 

  51. A.G. Rasin, J. Schiff, The Gardner method for symmetries. J. Phys. A 46, 155202 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  52. M. Wadati, H. Sanuki, K. Kanno, Relationships among inverse method, Bäcklund transformation and an infinite number of conservation laws. Prog. Theor. Phys. 53, 419–436 (1975)

    Article  ADS  MATH  Google Scholar 

  53. H. Mao, Y. Miao, Bäcklund transformation and nonlinear superposition formula for the two-component short pulse equation. J. Phys. A Math. Theor. 55, 475207 (2022)

    Article  ADS  MATH  Google Scholar 

  54. M. Xue, Q.P. Liu, H. Mao, Bäcklund transformations for the modified short pulse equation and complex modified short pulse equation. Eur. Phys. J. Plus 137, 500 (2022)

    Article  Google Scholar 

  55. A.G. Rasin, J. Schiff, Bäcklund transformations for the Camassa–Holm equation. J. Nonlinear Sci. 27, 45–69 (2017)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  56. G. Wang, Q.P. Liu, H. Mao, The modified Camassa–Holm equation: Bäcklund transformations and nonlinear superposition formula. J. Phys. A Math. Theor. 53, 294003 (2020)

    Article  MATH  Google Scholar 

  57. H. Mao, G. Wang, The Bäcklund transformations for Degasperis–Procesi equation. Theor. Math. Phys. 203, 747–760 (2020)

    Article  MATH  Google Scholar 

  58. Y. Zarmi, From single- to multiple-soliton solutions of the perturbed KdV equation. Phys. D 237, 2987–3007 (2008)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant No. 12261061) and the Natural Science Foundation of Guangxi Zhuang autonomous region, China (Grant No. 2022GXNSFAA035598).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Nanning Normal University, Nanning, 530001, Guangxi, People’s Republic of China

    Hui Mao

Authors
  1. Hui Mao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hui Mao.

Ethics declarations

Conflict of interest

The author declares that there is no conflict of interest regarding the publication of this paper.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mao, H. Multi-soliton solutions for the two-component modified short pulse equation and its nonlocal reductions via Bäcklund transformations. Eur. Phys. J. Plus 138, 769 (2023). https://doi.org/10.1140/epjp/s13360-023-04270-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-023-04270-0

Search

Navigation