Infinitely many conservation laws and Darboux-dressing transformation for the three-coupled fourth-order nonlinear Schrödinger equations

Abstract

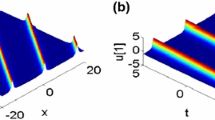
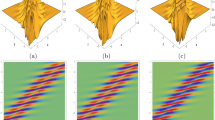
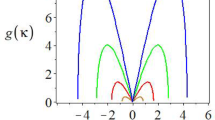
In this paper, we derive the infinitely many conservation laws through the Lax pair of the three-coupled fourth-order nonlinear Schrödinger equations and construct some semi-rational solutions by the Darboux-dressing transformation. These solutions contain breather waves, vector rogue waves, and the interaction between breather waves and vector rogue waves. Moreover, the dynamical behaviors of semi-rational solutions are discussed via some graphics

Appendix

The expressions of $g_{i}$ $(i=1,2,\ldots , 24)$ are as follows.

$$\begin{aligned}&g_{1}=4\varsigma _{1}h_{1},~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~g_{2}=-3\varsigma _{1}h_{1},\\&g_{3} =\varsigma _{1}\mathrm {i}\sin (\omega t) h_{1},~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~g_{4} =4\varsigma _{2} h_{1},\\&g_{5}=-3 \varsigma _{2} h_{1},~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~g_{6} =\varsigma _{2} \sin (\omega t) h_{1},\\&g_{7} =4 a_{i}^{2}\varsigma _{3} h_{1},~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~g_{8} = -3a_{i}^{2}\varsigma _{3} h_{1} -2 (\omega -a_{i}^{2}) \mathrm {i} \sin (\omega t) h_{2} ,\\&g_{9} =a_{i}^{2}\varsigma _{3} \sin (\omega t)\mathrm {i} h_{1}- (\omega -a_{i}^{2}) h_{2} ,~~~~~~~~~~~~~~g_{10} =-4\mathrm {i} h_{1},\\&g_{11} =3\varsigma _{3} h_{1}-2\mathrm {i} \sin (\omega t) h_{2},~~~~~~~~~~~~~~~~~~~~~~~~~~~g_{12} =- \mathrm {i} \sin (\omega t) \varsigma _{3} h_{1}- h_{2},\\&g_{13}=4 h_{3}h_{5},~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~g_{14}=-3h_{3}h_{5},\\&g_{15}=\mathrm {i} h_{3}h_{5}\sin (\gamma \omega ^{2} t),~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~g_{16}=-12 h_{3}h_{4},\\&g_{17}=9h_{3}h_{4},~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~g_{18}=-3\mathrm {i} h_{3}h_{4}\sin (\gamma \omega ^{2} t),\\&g_{19}=4 a_{i-1}^{2} h_{3}\mathrm {i} h_{7},~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~g_{20}=-3 a_{i-1}^{2} h_{3}\mathrm {i} h_{7}+48 \gamma \sin (\gamma \omega ^{2} t) (\omega - a_{i-1}^{2}) h_{6},\\&g_{21}=- a_{i-1}^{2} h_{3}h_{7}\sin (\gamma \omega ^{2} t)\\&\quad \quad \quad +24 \mathrm {i} \gamma (\omega - a_{i-1}^{2}) h_{6},~~~~~~~~~~~~~~~~~~~~~~~~~\!~~~~g_{22}=4 h_{3}\mathrm {i} h_{7},\\&g_{23}=-3 h_{3}\mathrm {i} h_{7}-48 \gamma \sin (\gamma \omega ^{2} t) h_{6},~~~~~~~~~~~~~~~g_{24}=- h_{3}h_{7}\sin (\gamma \omega ^{2} t)-24 \mathrm {i} \gamma h_{6}, \end{aligned}$$

where

$$\begin{aligned}&h_{1}=4 \cos (\gamma \omega ^{2} t)^{3}-4 \mathrm {i} \sin (\gamma \omega ^{2} t)\cos (\gamma \omega ^{2} t)^{2}-3 \cos (\gamma \omega ^{2} t) + \mathrm {i} \sin (\gamma \omega ^{2} t),\\&h_{2}= (2\cos (\gamma \omega ^{2} t)^{2}+2 \mathrm {i} \sin (\gamma \omega ^{2} t) \cos (\gamma \omega ^{2} t)-1),\\&h_{3}=4 \mathrm {i} \cos (\omega t)^{3} +4 \sin (\omega t) \cos (\omega t)^{2}-3 \mathrm {i} \cos (\omega t)-\sin (\omega t) ,\\&h_{4}=-288\gamma ^{3}\omega ^{5} t^{2}-144\gamma ^{2}\omega ^{4} t^{2}-24 \gamma \omega ^{3} t^{2}-24\mathrm {i} \gamma \omega ^{2} t-\frac{4}{3}\omega ^{2} t^{2}-4 \mathrm {i} \omega t+14\gamma \omega +1,\\&h_{5}=432\gamma ^{3}\omega ^{5} t^{2}+216\gamma ^{2}\omega ^{4} t^{2}+36\gamma \omega ^{3} t^{2}+108\mathrm {i} \gamma ^{2}\omega ^{3} t+2\omega ^{2} t^{2}+72 \mathrm {i}\gamma \omega ^{2} t-30\gamma \omega +9\mathrm {i} \omega t+6,\\&h_{6}=2 \cos (\omega t)^{2} -2 \mathrm {i} \cos (\omega t) \sin (\omega t) -1,\\&h_{7}=-432 \mathrm {i} \gamma ^{3} \omega ^{4} t^{2}-216 \mathrm {i} \gamma ^{2}\omega ^{3}t^{2}-36 \mathrm {i} \gamma \omega ^{2}t^{2}-108\gamma ^{2}\omega ^{2}t -2 \mathrm {i}\omega t^{2}+30 \mathrm {i} \gamma +3 t, \\&\varsigma _{1} = (-12 \mathrm {i} \gamma \omega ^{2}t-2\mathrm {i} \omega t+1 ),~~~~~~~~~~~~~~~\varsigma _{2} = (6 \mathrm {i} \gamma \omega +\mathrm {i}),~~~~~~~~~~~~~~~\varsigma _{3} = (12 \mathrm {i} \gamma \omega ^{2}t+2\mathrm {i} \omega t+1 ). \end{aligned}$$