Skip to main content

Advertisement

SpringerLink
Log in

Effect of two-temperature on the energy ratios at the elastic–piezothermoelastic interface with phase lags

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

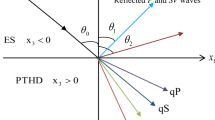
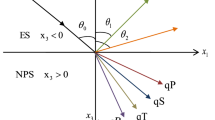
The phenomenon of reflection and transmission of plane waves between two half-spaces elastic and orthotropic piezothermoelastic with three-phase-lag and two-temperature is investigated. Amplitude ratios of the waves are obtained and used to compute energy ratios. The trend of energy ratios of different reflected and transmitted waves with angle of incidence is displayed graphically depicting the effect of two-temperature parameters with the consideration of three-phase-lag theory. The conservation of energy is justified. A particular case is also deduced from the study.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig.3
Fig.4
Fig.5
Fig.6

Similar content being viewed by others

Availability of data and material

All data generated or analysed during this study are included in this article.

Abbreviations

OPTHS:

Orthotropic piezothermoelastic half-space

ES:

Elastic half-space

WTT:

Energy ratio curves for orthotropic piezothermoelastic with phase lags and two-temperature

WOTT:

Energy ratio curves for orthotropic piezothermoelastic with phase lags and without two-temperature

\(c_{ijkl}\) :

Elastic parameters

\(\alpha_{ij}\) :

Tensor of thermal moduli

\(\rho\) :

Mass density

\(C_{e}\) :

Specific heat at constant strain

\(T_{0} ,\,T\) :

Reference temperature, absolute temperature

\(\sigma_{ij} {,}\varepsilon_{ij}\) :

Components of the stress and strain tensor in OPTHS

\(E_{i}\) :

Electric field intensity

\(D_{i}\) :

Electric displacement

\(\phi\) :

Electric potential

\(\tau_{i}\) :

Pyroelectric constants

\(e_{ijk} ,\xi_{ij}\) :

Tensors of piezothermal moduli

\(u_{i} ,\,u_{i}^{e}\) :

Components of displacement vectors in OPTHS and ES, respectively

\(\,\tau_{t} ,\,\tau_{\nu } ,\tau_{q}\) :

Phase lags of temperature gradient, thermal displacement gradient and heat flux, respectively, such that \(0 \le \tau_{\nu } < \tau_{t} < \tau_{q}\)

\(K_{ij} ,K_{ij}^{*}\) :

Components of thermal conductivity and material constant

\(\varphi\) :

Conductive temperature of the medium

\(\nu\) :

Thermal displacement

\(\rho^{e} ,\lambda^{e} ,\mu^{e}\) :

Mass density and the Lame’s constants in elastic media, respectively

\(\sigma_{ij}^{e} ,\,\,\varepsilon_{ij}^{e}\) :

Components of the stress and strain tensor in ES

References

  1. S.K. Roy Choudhury, J. Therm Stresses, 231 (2007)

  2. P.J. Chen, W.O. Williams, Z. Angew. Math. Phys., 969 (1968)

  3. P.J. Chen, M.E. Gurtin, Z. Angew. Math. Phys., 614 (1968)

  4. P. J. Chen, M.E. Gurtin, W.O. Williams, Z. Angew. Math. Phys., 107 (1969)

  5. M.I.A. Othman, K. Lotfy, MMMS, 43 (2011)

  6. K. Lotfy, S.M. Abo-Dahab, J. Comput. Theor. Nanosci., 1709 (2015)

  7. M.I.A. Othman, K. Lotfy, J. Comput. Theor. Nanosci., 2587 (2015)

  8. S.M. Abo-Dahab, K. Lotfy, A. Gohaly, Math. Probl. Eng., 15 (2015)

  9. R. Kumar, S. Devi, S. Abo-Dahab, Waves Random Complex Media, 1 (2019)

  10. K. Lotfy, W. Hassan, A.A. El-Bary, M.A. Kadry, Results Phys., 102877 (2020)

  11. A.M. Zenkour, D.S. Mashat, Sci Rep, 4417 (2020)

  12. P. Lata, Appl. Appl. Math., 1216 (2018)

  13. S.M. Said, Y.D. Elmaklizi, M.I.A. Othman, Chaos Solitons Fractals, 75 (2017)

  14. R. Kumar, A.K. Vashishth, S. Ghangas, Mater. Phys. Mech., 126 (2018)

  15. M.A. Ezzat, A.S. El-Karamany, A.A. El-Bary, Microsyst. Technol., 951 (2018)

  16. S. Deswal, S.K. Sheokand, K.K. Kalkal, Appl. Math. Model., 106 (2019)

  17. M. Othman S. Said, M. Marin, Int. J. Numer. Methods Heat Fluid Flow, 4788 (2019)

  18. R.D. Mindlin, Int. J. Solids Struc., 625 (1974)

  19. W. Nowacki, J. Therm Stresses, 171 (1978)

  20. W. Nowacki, in Parkus, H. (Ed.), Electromagnetic Interactions in Elastic Solids, (Springer, Wein, 1979), Chapter 1

  21. M.D. Sharma, Acta Mech., 307 (2010)

  22. A.K. Vashishth, H. Sukhija, Appl. Math. Mech. Engl. Ed., 11 (2015)

  23. R. Kumar, P. Sharma, Coupled Sys. Mech., 157 (2017)

  24. R. Kumar, P. Sharma, Appl. Math. Comp., 194 (2019)

  25. J.D. Achenbach, North Holland Pub., (Amsterdam, 1973)

  26. H.S. Tzou, Y. Bao, J. Sounds Vib., 453 (1995).

  27. K.E. Bullen, Cambridge University Press, U.K. (1963).

Download references

Funding

No funding was received for conducting this study.

Author information

Authors and Affiliations

  1. Department of Mathematics, Kurukshetra University, Kurukshetra, Haryana, 136119, India

    Rajneesh Kumar & Poonam Sharma

Authors
  1. Rajneesh Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Poonam Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Poonam Sharma.

Ethics declarations

Conflict of interest

No conflict of interest.

Code availability

Software application is stated in this article.

Appendices

Appendix A

$$ \begin{aligned} t_{11} & = T_{0} (i\omega - \omega^{2} \tau_{0} ),t_{12} = \frac{{\alpha_{11} T_{0} }}{{e_{31} }},t_{13} = - \frac{{i\rho c_{1}^{2} }}{\omega c},t_{14} = 1 + \omega^{2} \frac{{a_{11} }}{{c^{2} }},\\ t_{15} & = \omega^{2} a_{33} ,t_{16} = - \frac{{i\rho c_{1}^{2} \alpha_{33} }}{{\omega \alpha_{11} }}, t_{17} = - \frac{\rho }{{\alpha_{11} }},t_{18} = t_{17} \omega_{1} \omega^{2} ,\\ t_{19} & = - t_{11} c_{1}^{2} r,\,{\text{where}}\,r = \frac{{\rho C_{e} }}{{T_{0} }},t_{20} = \frac{{i\rho c_{1}^{2} \tau_{3} }}{{\omega \alpha_{11} }}\tau_{T} = (1 + i\omega \tau_{t} ), \\ \tau_{X} & = (1 + i\omega \tau_{\upsilon } ),_{Q} = (1 + i\omega \tau_{q} - \frac{{\omega^{2} }}{2}\tau_{q}^{2} ),\\ t_{11} & = \frac{{\alpha_{11} T_{0} }}{{e_{31} }},t_{12} = - \frac{{i\rho c_{1}^{2} }}{\omega c}, \\ t_{13} & = 1 + \omega^{2} \frac{{a_{11} }}{{c^{2} }}, t_{14} = \omega^{2} a_{33} ,t_{15} = - \frac{{i\rho c_{1}^{2} \alpha_{33} }}{{\omega \alpha_{11} }},t_{16} = \frac{{i\omega \rho \omega_{1} \tau_{T} }}{{\alpha_{11} }},t_{17} = \frac{{\rho \tau_{X} }}{{\alpha_{11} }}, \\ t_{18} & = - \frac{{\rho c_{1}^{2} \tau_{Q} T_{0} r}}{{\alpha_{11} }}\,{\text{where}}\,r = \frac{{\rho C_{e} }}{{T_{0} }},t_{19} = \frac{{i\rho c_{1}^{2} \tau_{3} }}{{\omega \alpha_{11} }}. \\ x_{11} & = \frac{{c_{11} }}{{c^{2} }} - \rho c_{1}^{2} ,x_{12} = \frac{{(c_{13} + c_{55} )}}{c} = x_{16} ,x_{13} = \frac{{(e_{31} + e_{15} )}}{c}t_{11} ,\\ x_{14} & = t_{12} t_{13} ,x_{15} = t_{12} t_{14} ,x_{17} = \frac{{c_{55} }}{{c^{2} }} - \rho c_{1}^{2} , \\ x_{18} & = \frac{{t_{11} e_{15} }}{{c^{2} }},x_{19} = t_{11} e_{33} ,x_{20} = t_{13} t_{15} ,x_{21} = t_{15} t_{14} ,x_{22} = \frac{{i\omega \alpha_{11} \tau_{Q} T_{0} }}{c},\\ x_{23} &= i\omega \alpha_{33} \tau_{Q} T_{0} , x_{24} = - \frac{{i\omega \tau_{Q} \left( {T_{0} } \right)^{2} \tau_{3} \alpha_{11} }}{{e_{31} }},x_{25} = \frac{{t_{16} K_{11} }}{{c^{2} }} + \frac{{t_{17} K_{{_{11} }}^{ * } }}{{c^{2} }} + t_{13} t_{18} ,\\ x_{26} & = t_{16} K_{33} + t_{17} K_{{_{33} }}^{ * } + t_{14} t_{18} , x_{27} = \frac{{(e_{31} + e_{15} )}}{c},x_{28} = \frac{{e_{15} }}{{c^{2} }},x_{29} = - \frac{{t_{11} \xi_{11} }}{{c^{2} }},\\ x_{30} & = - t_{11} \xi_{33} ,x_{31} = t_{13} t_{19} ,x_{32} = t_{14} t_{19} . b_{11} = x_{17} x_{33} - x_{18} x_{32} ,b_{12} = c_{33} x_{33} + x_{17} x_{34} ,\\ b_{13} & = - (x_{19} x_{32} + x_{18} e_{33} ),b_{14} = b_{12} + b_{13} ,b_{15} = x_{18} e_{33} - c_{55} x_{33} , \\ b_{16} & = x_{12} x_{33} - x_{18} x_{31} ,b_{17} = x_{12} x_{34} - x_{19} x_{31} ,\\ b_{18} &= x_{12} x_{32} - x_{17} x_{31} ,b_{19} = x_{12} e_{33} - c_{33} x_{31} , \\ b_{20} & = c_{55} b_{11} + x_{11} b_{14} - x_{12} b_{16} + x_{13} b_{18} ,b_{21} = \,c_{55} b_{14} + x_{11} b_{15} - x_{12} b_{17} + x_{13} b_{19} . \\ m_{11} & = - c_{55} x_{26} b_{19} ,m_{12} = - (b_{19} x_{25} c_{55} + x_{26} b_{21} ),\\ m_{13} & = - (b_{21} x_{25} + b_{20} x_{26} ),m_{14} = - (b_{20} x_{25} + x_{26} x_{11} b_{17} ), \\ m_{15} & = - x_{11} x_{25} b_{17} . \\ \end{aligned} $$

Appendix B

$$ \begin{aligned} D_{{1i}} & = - \frac{{c_{{13}} }}{c} - c_{{33}} q_{i} W_{i} - \frac{{\alpha _{{11}} T_{0} e_{{33}} }}{{e_{{31}} }}q_{i} \Phi _{i} - \frac{{\alpha _{{33}} \rho c_{1}^{2} }}{{i\omega \alpha _{{11}} }}\left( {1 + \omega ^{2} \frac{{a_{{11}} }}{{c^{2} }} + \omega ^{2} a_{{33}} q_{i}^{2} } \right)\Theta _{i} ,\,\,\, \\ D_{{2i}} & = - c_{{55}} \left( {\frac{{W_{i} }}{c} + q_{i} } \right) + \frac{{e_{{15}} c_{1} \alpha _{{11}} T_{0} }}{{ce_{{31}} \omega _{1} }}\Phi _{i} ,\,\,D_{{3i}} = 1\,\,,\\ D_{{4i}} & = W_{i} ,\,\,\,D_{{5i}} = \left( {1 + \omega ^{2} \frac{{a_{{11}} }}{{c^{2} }} + \omega ^{2} a_{{33}} q_{i}^{2} } \right)q_{i} \Theta _{i} ,\,\, \\ D_{{6i}} & = - \frac{{e_{{31}} }}{c}\, - e_{{33}} q_{i} W_{i} + \frac{{\xi _{{33}} T_{0} \alpha _{{11}} }}{{e_{{31}} }}q_{i} \Phi _{i}\\ &\quad + \frac{{\tau _{3} \rho c_{1}^{2} }}{{i\omega \alpha _{{11}} }}\left( {1 + \omega ^{2} \frac{{a_{{11}} }}{{c^{2} }} + \omega ^{2} a_{{33}} q_{i}^{2} } \right)\Theta _{i} \,,\,(i = 1,2,3,4). \\ \end{aligned} $$
  1. (i)

    For incident P wave

$$ \begin{aligned} D_{{15}} & = - i\omega \rho ^{e} c_{1}^{2} \left( {1 - \frac{{2\beta ^{{e^{2} }} \sin ^{2} \theta }}{{\alpha ^{{e^{2} }} }}} \right),\,\,\,D_{{16}} = i\omega \rho ^{e} c_{1}^{2} \sin 2\theta _{2} ,\,\,D_{{25}} = \frac{{i\omega \beta ^{{e^{2} }} \rho ^{e} c_{1}^{2} \sin 2\theta }}{{\alpha ^{{e^{2} }} }},\,\, \\ D_{{26}} & = i\omega \rho ^{e} c_{1}^{2} \cos 2\theta _{2} ,\,\,\,D_{{35}} = \frac{{i\omega c_{1} \sin \theta }}{{\alpha ^{e} }},\,\,\,D_{{36}} = \frac{{i\omega c_{1} \cos \theta _{2} }}{{\beta ^{e} }},\\ D_{{45}} & = - \frac{{i\omega c_{1} \cos \theta }}{{\alpha ^{e} }},\,\,D_{{46}} = \frac{{i\omega c_{1} \sin \theta _{2} }}{{\beta ^{e} }}, \\ X_{i} & = \frac{{U_{i} }}{{A_{0}^{e} }},\,(i = 1,2,3,4),\,\,X_{5}^{e} = \frac{{A_{1}^{e} }}{{A_{0}^{e} }},X_{6}^{e} = \frac{{B_{1}^{e} }}{{A_{0}^{e} }},\\ N_{1} &= - D_{{15}} ,\,\,N_{2} = D_{{25}} ,\,\,N_{3} = - D_{{35}} ,\,\,N_{4} = D_{{45}} . \\ \end{aligned} $$
  1. (ii)

    For incident SV wave

$$ \begin{aligned} D_{{15}} & = - i\omega \rho ^{e} c_{1}^{2} \left( {1 - \frac{{2\beta ^{{e^{2} }} \sin ^{2} \theta _{1} }}{{\alpha ^{{e^{2} }} }}} \right),\,\,\,D_{{16}} = i\omega \rho ^{e} c_{1}^{2} \sin 2\theta ,\,\,D_{{25}} = \frac{{i\omega \beta ^{{e^{2} }} \rho ^{e} c_{1}^{2} \sin 2\theta _{1} }}{{\alpha ^{{e^{2} }} }},\,\, \\ D_{{26}} & = i\omega \rho ^{e} c_{1}^{2} \cos 2\theta ,\,\,\,D_{{35}} = \frac{{i\omega c_{1} \sin \theta _{1} }}{{\alpha ^{e} }},\,\,\,D_{{36}} = \frac{{i\omega c_{1} \cos \theta }}{{\beta ^{e} }},\\ D_{{45}} & = - \frac{{i\omega c_{1} \cos \theta _{1} }}{{\alpha ^{e} }},\,\,D_{{46}} = \frac{{i\omega c_{1} \sin \theta }}{{\beta ^{e} }}, \\ X_{i} & = \frac{{U_{i} }}{{B_{0}^{e} }},\,(i = 1,2,3,4),\,\,X_{5}^{e} = \frac{{A_{1}^{e} }}{{B_{0}^{e} }},X_{6}^{e} = \frac{{B_{1}^{e} }}{{B_{0}^{e} }},\,\,N_{1} = D_{{16}} ,\\ N_{2}& = - D_{{26}} ,\,\,N_{3} = D_{{36}} ,\,\,N_{4} = - D_{{46}} . \\ \end{aligned} $$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumar, R., Sharma, P. Effect of two-temperature on the energy ratios at the elastic–piezothermoelastic interface with phase lags. Eur. Phys. J. Plus 136, 1200 (2021). https://doi.org/10.1140/epjp/s13360-021-02042-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-021-02042-2

Search

Navigation