Skip to main content
SpringerLink
Log in

Natural frequency calculation of open laminated conical and cylindrical shells by a meshless method

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

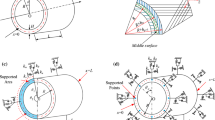
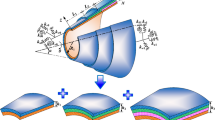
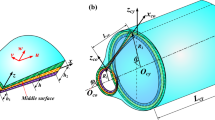
In this paper, a new and an efficient solution method based on local gradient smoothing method has been applied to free vibration problem of open composite laminated cylindrical and conical shells with elastic boundary conditions. The theoretical model is formulated by the first-order shear deformation theory, and the motion equation is obtained by the Hamilton’s principle. The motion equation is discretized by meshless shape function; in this process, the derivatives of the shape function are approximated by local gradient smoothing method. The accuracy, applicability and efficiency of this method are demonstrated for free vibrations of open composite laminated cylindrical and conical shells with different geometric, material parameters and boundary condition. The numerical results show good convergence characteristics and good agreement between the present method and the existing literature. And through several numerical examples, some useful results for free vibration results of open composite laminated cylindrical and conical shells are obtained, which may serve as a benchmark solutions for researchers to check their analytical and numerical methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Data Availability Statement

This manuscript has associated data in a data repository. [Authors’ comment: All data included in this manuscript are available upon request by contacting with the corresponding author.]

References

  1. A.W. Leissa, R.P. Nordgren, Vibration of Shells (NASA SP-288) (US: Government Printing Office, Washington, 1973)

    Google Scholar 

  2. C. Shu, Free vibration analysis of composite laminated conical shells by generalized differential quadrature. J. Sound Vib. 194(4), 587–604 (1996)

    ADS  MATH  Google Scholar 

  3. L. Hua, Frequency characteristics of a rotating truncated circular layered conical shell. Compos. Struct. 50(1), 59–68 (2000)

    MathSciNet  Google Scholar 

  4. Y. Ng, L. Hua, K.Y. Lam, Generalized differential quadrature for free vibration of rotating composite laminated conical shell with various boundary conditions. Int. J. Mech. Sci. 45(3), 567–587 (2003)

    MATH  Google Scholar 

  5. Ö. Civalek, Numerical analysis of free vibrations of laminated composite conical and cylindrical shells. J. Comput. Appl. Math. 205(1), 251–271 (2007)

    ADS  MathSciNet  MATH  Google Scholar 

  6. Ö. Civalek, Vibration analysis of laminated composite conical shells by the method of discrete singular convolution based on the shear deformation theory. Compos. B Eng. 45(1), 1001–1009 (2013)

    Google Scholar 

  7. Y. Qu, X. Long, S. Wu, G. Meng, A unified formulation for vibration analysis of composite laminated shells of revolution including shear deformation and rotary inertia. Compos. Struct. 98, 169–191 (2013)

    Google Scholar 

  8. K.K. Viswanathan, J.H. Lee, Z.A. Aziz, I. Hossain, R. Wang, H.Y. Abdullah, Vibration analysis of cross-ply laminated truncated conical shells using a spline method. J. Eng. Math. 76, 139–156 (2012)

    MathSciNet  Google Scholar 

  9. C. Wu, C. Lee, Differential quadrature solution for the free vibration analysis of laminated conical shells with variable stiffness. Int. J. Mech. Sci. 43(8), 1853–1869 (2001)

    MATH  Google Scholar 

  10. I.F.P. Correia, C.M.M. Soares, C.A.M. Soares, J. Herskovits, Analysis of laminated conical shell structures using higher order models. Compos. Struct. 62(3–4), 383–390 (2003)

    Google Scholar 

  11. J.N. Reddy, C.F. Liu, A higher-order shear deformation theory of laminated elastic shells. Int. J. Eng. Sci. 23(3), 319–330 (1985)

    MATH  Google Scholar 

  12. A.J.M. Ferreira, C.M.C. Roque, R.M.N. Jorge, Modelling cross-ply laminated elastic shells by a higher-order theory and multiquadrics. Comput. Struct. 84(19–20), 1288–1299 (2006)

    Google Scholar 

  13. A.J.M. Ferreira, C.M.C. Roque, R.M.N. Jorge, Static and free vibration analysis of composite shells by radial basis functions. Eng. Anal. Bound. Elem. 30(9), 719–733 (2006)

    MATH  Google Scholar 

  14. M. Ganapathi, B.P. Patel, D.S. Pawargi, Dynamic analysis of laminated cross-ply composite non-circular thick cylindrical shells using higher-order theory. Int. J. Solids Struct. 39(24), 5945–5962 (2002)

    MATH  Google Scholar 

  15. B. Damjan, M. Bacciocchi, F. Tornabene, Influence of Winkler–Pasternak foundation on the vibrational behavior of plates and shells reinforced by agglomerated carbon nanotubes. Appl. Sci. 7(12), 1–55 (2017)

    Google Scholar 

  16. F. Tornabene, Free vibrations of anisotropic doubly-curved shells and panels of revolution with a free-form meridian resting on Winkler–Pasternak elastic foundations. Compos. Struct. 94(1), 186–206 (2011)

    Google Scholar 

  17. F. Tornabene, A. Ceruti, Free-form laminated doubly-curved shells and panels of revolution resting on Winkler–Pasternak elastic foundations: a 2-D GDQ solution for static and free vibration analysis. World J. Mech. 3(1), 1–25 (2013)

    Google Scholar 

  18. F. Tornabene, J. Reddy, FGM and laminated doubly-curved and degenerate shells resting on nonlinear elastic foundations: a GDQ solution for static analysis with a posteriori stress and strain recovery. J. Indian Inst. Sci. 93(4), 635–688 (2013)

    MathSciNet  Google Scholar 

  19. F. Tornabene, N. Fantuzzi, E. Viola, J.N. Reddy, Winkler-Pasternak foundation effect on the static and dynamic analyses of laminated doubly-curved and degenerate shells and panels. Compos. B Eng. 57, 269–296 (2014)

    Google Scholar 

  20. B. Qin, R. Zhong, T. Wang, Q. Wang, Y. Xue, Z. Hu, A unified Fourier series solution for vibration analysis of FG-CNTRC cylindrical, conical shells and annular plates with arbitrary boundary conditions. Compos. Struct. 232(15), 111549 (2020)

    Google Scholar 

  21. H. Zhang, D. Shi, Q. Wang, An improved Fourier series solution for free vibration analysis of the moderately thick laminated composite rectangular plate with non-uniform boundary conditions. Int. J. Mech. Sci. 121, 1–20 (2017)

    Google Scholar 

  22. H. Zhang, H. Hong, D. Shi, S. Zha, Q.Wang, A modified Fourier solution for sound-vibration analysis for composite laminated thin sector platecavity coupled system. Compos. Struct. 207, 560–575 (2019)

    Google Scholar 

  23. D. Shi, G. Liu, H. Zhang, W. Ren, Q. Wang, A three-dimensional modeling method for the trapezoidal cavity and multi-coupled cavity with various impedance boundary conditions. Appl. Acoust. 154, 213–225 (2019)

    Google Scholar 

  24. G. Jin, T. Ye, Y. Chen, Z. Su, Y. Yan, An exact solution for the free vibration analysis of laminated composite cylindrical shells with general elastic boundary conditions. Compos. Struct. 106(12), 114–127 (2013)

    Google Scholar 

  25. G. Jin, T. Ye, X. Ma, Y. Chen, Z. Su, X. Xie, A unified approach for the vibration analysis of moderately thick composite laminated cylindrical shells with arbitrary boundary conditions. Int. J. Mech. Sci. 75(10), 357–376 (2013)

    Google Scholar 

  26. J. Zhao, K. Choe, C. Shuai, A. Wang, Q. Wang, Free vibration analysis of functionally graded carbon nanotube reinforced composite truncated conical panels with general boundary conditions. Compos. B Eng. 160(1), 225–240 (2019)

    Google Scholar 

  27. K. Choe, K. Kim, Q. Wang, Dynamic analysis of composite laminated doubly-curved revolution shell based on higher order shear deformation theory. Compos. Struct. 225(1), 111155 (2019)

    Google Scholar 

  28. B. Qin, K. Choe, Q. Wu, T. Wang, Q. Wang, A unified modeling method for free vibration of open and closed functionally graded cylindrical shell and solid structures. Compos. Struct. 223(1), 110941 (2019)

    Google Scholar 

  29. B. Qin, K. Choe, T. Wang, Q. Wang, A unified Jacobi–Ritz formulation for vibration analysis of the stepped coupled structures of doubly-curved shell. Compos. Struct. 220, 717–735 (2019)

    Google Scholar 

  30. J. Zhao, K. Choe, C. Shuai, A. Wang, Q. Wang, Free vibration analysis of laminated composite elliptic cylinders with general boundary conditions. Compos. B Eng. 158, 55–66 (2019)

    Google Scholar 

  31. K. Choe, Q. Wang, J. Tang, C. Shuai, Vibration analysis for coupled composite laminated axis-symmetric doubly-curved revolution shell structures by unified Jacobi–Ritz method. Compos. Struct. 194, 136–157 (2018)

    Google Scholar 

  32. H. Haftchenari, M. Darvizeh, A. Darvizeh, R. Ansari, C.B. Sharma, Dynamic analysis of composite cylindrical shells using differential quadrature method (DQM). Compos. Struct. 78(2), 292–298 (2007)

    Google Scholar 

  33. F. Tornabene, N. Fantuzzi, M. Bacciocchi, J.N. Reddy, A posteriori stress and strain recovery procedure for the static analysis of laminated shells resting on nonlinear elastic foundation. Compos. B Eng. 126, 162–191 (2017)

    Google Scholar 

  34. Y. Qu, H. Hua, G. Meng, A domain decomposition approach for vibration analysis of isotropic and composite cylindrical shells with arbitrary boundaries. Compos. Struct. 95, 307–321 (2013)

    Google Scholar 

  35. X. Xie, G. Jin, W. Li, Z. Liu, A numerical solution for vibration analysis of composite laminated conical, cylindrical shell and annular plate structures. Compos. Struct. 111, 20–30 (2014)

    Google Scholar 

  36. R. Talebitooti, V.S. Anbardan, Haar wavelet discretization approach for frequency analysis of the functionally graded generally doubly-curved shells of revolution. Appl. Math. Model. 67, 645–675 (2019)

    MathSciNet  MATH  Google Scholar 

  37. X. Zhao, K.M. Liew, T.Y. Ng, Vibration analysis of laminated composite cylindrical panels via a meshfree approach. Int. J. Solids Struct. 40(1), 161–180 (2003)

    MATH  Google Scholar 

  38. K.M. Liew, X. Zhao, A.J.M. Ferreira, A review of meshless methods for laminated and functionally graded plates and shells. Compos. Struct. 93(8), 2031–2041 (2011)

    Google Scholar 

  39. H. Assaee, H. Hasani, Forced vibration analysis of composite cylindrical shells using spline finite strip method. Thin-Walled Struct. 97, 207–214 (2015)

    Google Scholar 

  40. N.S. Bardell, R.S. Langley, J.M. Dunsdon, G.S. Aglietti, An h-p finite element vibration analysis of open conical sandwich panels and conical sandwich frusta. J. Sound Vib. 226(2), 345–377 (1999)

    ADS  Google Scholar 

  41. G.R. Liu, Y.T. Gu, An Introduction to Meshfree Methods and Their Programming (Springer, Dordrecht, 2005)

    Google Scholar 

  42. B. Chinnaboon, S. Chucheepsakul, J.T. Katsikadelis, A BEM-based domain meshless method for the analysis of Mindlin plates with general boundary conditions. Comput. Methods Appl. Mech. Eng. 200(13–16), 1379–1388 (2011)

    ADS  MathSciNet  MATH  Google Scholar 

  43. J. Sorić, T. Jarak, Mixed meshless formulation for analysis of shell-like structures. Comput. Methods Appl. Mech. Eng. 199(17–20), 1153–1164 (2010)

    ADS  MathSciNet  MATH  Google Scholar 

  44. W. Li, Z.X. Gong, Y.B. Chai, C. Cheng, T.Y. Li, Q.F. Zhang, M.S. Wang, Hybrid gradient smoothing technique with discrete shear gap method for shell structures. Comput. Math Appl. 74(8), 1826–1855 (2017)

    MathSciNet  MATH  Google Scholar 

  45. M.R. Moghaddam, G.H. Baradaran, Three-dimensional free vibrations analysis of functionally graded rectangular plates by the meshless local PetrovGalerkin (MLPG) method. Appl. Math. Comput. 304, 153–163 (2017)

    MathSciNet  MATH  Google Scholar 

  46. E. Shivanian, Meshless local Petrov–Galerkin (MLPG) method for three-dimensional nonlinear wave equations via moving least squares approximation. Eng. Anal. Bound. Elem. 50, 249–257 (2015)

    MathSciNet  MATH  Google Scholar 

  47. P.H. Wen, Meshless local Petrov–Galerkin (MLPG) method for wave propagation in 3D poroelastic solids. Eng. Anal. Bound. Elem. 34(4), 315–323 (2010)

    MathSciNet  MATH  Google Scholar 

  48. I. Alfaro, J. Yvonnet, E. Cueto, F. Chinesta, M. Doblare, Meshless methods with application to metal forming. Comput. Methods Appl. Mech. Eng. 195(48–49), 6661–6675 (2006)

    ADS  MathSciNet  MATH  Google Scholar 

  49. Z. Mao, G.R. Liu, A Lagrangian gradient smoothing method (L-GSM) for solid-flow problems using simplicial mesh. Int. J. Numer. Methods Eng. 113, 858–890 (2017)

    Google Scholar 

  50. D. Hui, G.Y. Zhang, D.P. Yu, Z. Sun, Z. Zong, Numerical study of advection schemes for interface-capturing using gradient smoothing method. Numer. Heat Transf. B Fundam. 73(4), 242–261 (2018)

    ADS  Google Scholar 

  51. J. Yao, G.R. Liu, D. Qian, C. Chen, G.X. Xu, A moving-mesh gradient smoothing method for compressible CFD problems. Math. Models Methods Appl. Sci. 23(02), 273–305 (2013)

    MathSciNet  MATH  Google Scholar 

  52. E. Li, V. Tan, G.X. Xu, G.R. Liu, Z.C. He, A novel alpha gradient smoothing method (αGSM) for fluid problems. Numer. Heat Transf. B Fundam. 61(3), 204–228 (2012)

    ADS  Google Scholar 

  53. B. Shao, G.R. Liu, T. Lin, G.X. Xu, X. Yan, Rotation and orientation of irregular particles in viscous fluids using the gradient smoothed method (GSM). Eng. Appl. Comput. Fluid Mech. 11(1), 557–575 (2017)

    Google Scholar 

  54. G.X. Xu, G.R. Liu, A. Tani, An adaptive gradient smoothing method (GSM) for fluid dynamics problems. Int. J. Numer. Methods Fluids 62(5), 499–529 (2009)

    MathSciNet  MATH  Google Scholar 

  55. Z. Han, H.T. Liu, A. Rajendran, S.N. Atluri, The applications of meshless local Petrov–Galerkin (MLPG) approaches in high-speed impact, penetration and perforation problems. Comput. Model. Eng. Sci. 14(2), 119–128 (2006)

    MathSciNet  MATH  Google Scholar 

  56. G.R. Liu, An overview on meshfree methods: for computational solid mechanics. Int. J. Comput. Methods 13(05), 1630001 (2016)

    ADS  MathSciNet  MATH  Google Scholar 

  57. S. Daxini, J. Prajapati, A review on recent contribution of meshfree methods to structure and fracture mechanics applications. Sci. World J. 1, 1–13 (2014)

    Google Scholar 

  58. J. Zhang, G.R. Liu, K.Y. Lam, H. Li, G. Xu, A gradient smoothing method (GSM) based on strong form governing equation for adaptive analysis of solid mechanics problems. Finite Elem. Anal. Des. 44(15), 889–909 (2008)

    MathSciNet  Google Scholar 

  59. G.R. Liu, B.B.T. Kee, L. Chun, A stabilized least-squares radial point collocation method (LS-RPCM) for adaptive analysis. Comput. Methods Appl. Mech. Eng. 195(37–40), 4843–4861 (2006)

    ADS  MathSciNet  MATH  Google Scholar 

  60. F. Auricchio, L.B. Da Veiga, T.J.R. Hughes, A. Reali, G. Sangalli, Isogeometric collocation methods. Math. Models Methods Appl. Sci. 20(11), 2075–2107 (2010)

    MathSciNet  MATH  Google Scholar 

  61. E. Oñate, F. Perazzo, J. Miquel, A finite point method for elasticity problems. Comput. Struct. 79(22–25), 2151–2163 (2001)

    Google Scholar 

  62. A. Karamanli, A. Mugan, Strong form meshless implementation of Taylor series method. Appl. Math. Comput. 219(17), 9069–9080 (2013)

    MathSciNet  MATH  Google Scholar 

  63. D.D. Wang, J.C. Wu, An efficient nesting sub-domain gradient smoothing integration algorithm with quadratic exactness for Galerkin meshfree methods. Comput. Methods Appl. Mech. Eng. 298, 485–519 (2016)

    ADS  MathSciNet  MATH  Google Scholar 

  64. G.R. Liu, J. Zhang, K.Y. Lam, H. Li, G. Xu, Z.H. Zhong, G.Y. Li, X. Han, A gradient smoothing method (GSM) with directional correction for solid mechanics problems. Comput. Mech. 41(3), 457–472 (2008)

    MATH  Google Scholar 

  65. M.S. Qatu, Vibration of Laminated Shells and Plates (Elsevier, San Diego, 2004)

    MATH  Google Scholar 

  66. T. Ye, G. Jin, Z. Su, X. Jia, A unified Chebyshev-Ritz formulation for vibration analysis of composite laminated deep open shells with arbitrary boundary conditions. Arch. Appl. Mech. 84(4), 441–471 (2014)

    ADS  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Mechanical Science and Technology, Kim Chaek University of Technology, Pyongyang, 999093, Democratic People’s Republic of Korea

    Songhun Kwak & Gwangil Jong

  2. Department of Engineering Machine, Pyongyang University of Mechanical Engineering, Pyongyang, 999093, Democratic People’s Republic of Korea

    Kwanghun Kim, Yonguk Ri & Hyonil Ri

Authors
  1. Songhun Kwak
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kwanghun Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yonguk Ri
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Gwangil Jong
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Hyonil Ri
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kwanghun Kim.

Appendix

Appendix

$$ \varvec{K}_{Ii} = \left[ {\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} {L_{11} } & {L_{12} } & {L_{13} } & {L_{14} } & {L_{15} } \\ {L_{21} } & {L_{22} } & {L_{23} } & {L_{24} } & {L_{25} } \\ {L_{31} } & {L_{32} } & {L_{33} } & {L_{34} } & {L_{35} } \\ {L_{41} } & {L_{42} } & {L_{43} } & {L_{44} } & {L_{45} } \\ {L_{51} } & {L_{52} } & {L_{53} } & {L_{54} } & {L_{55} } \\ \end{array} } \right],\,\varvec{M}_{Ii} = \left[ {\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} { - I_{0} \phi_{i} } & 0 & 0 & { - I_{1} \phi_{i} } & 0 \\ 0 & { - I_{0} \phi_{i} } & 0 & 0 & 0 \\ 0 & 0 & { - I_{0} \phi_{i} } & 0 & 0 \\ { - I_{1} \phi_{i} } & 0 & 0 & { - I_{2} \phi_{i} } & 0 \\ 0 & { - I_{1} \phi_{i} } & 0 & 0 & { - I_{2} \phi_{i} } \\ \end{array} } \right] $$

Detailed expressions of differential operators \( L_{ij} \):

$$ L_{11} = A_{11} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{2A_{16} }}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{A_{66} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + A_{11} \frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x} - A_{22} \frac{{\sin^{2} \varphi }}{{R^{2} }}\phi_{i} $$
$$ \begin{aligned} L_{12} & = A_{16} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{(A_{12} + A_{66} )}}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{A_{26} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + (A_{16} - A_{26} )\frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x}\\ & - (A_{22} + A_{66} )\frac{\sin \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } + A_{26} \frac{{\sin^{2} \varphi }}{{R^{2} }}\phi_{i} \\ \end{aligned} $$
$$ L_{13} = A_{12} \frac{\cos \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x} + A_{26} \frac{\cos \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } - A_{22} \frac{\sin \varphi \cos \varphi }{{R^{2} }}\phi_{i} $$
$$ L_{14} = B_{11} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{2B_{16} }}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{B_{66} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + B_{11} \frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x} - B_{22} \frac{{\sin^{2} \varphi }}{{R^{2} }}\phi_{i} $$
$$ \begin{aligned} L_{15} & = B_{16} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{(B_{12} + B_{66} )}}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{B_{26} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + (B_{16} - B_{26} )\frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x}\\ & - (B_{22} + B_{66} )\frac{\sin \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } + B_{26} \frac{{\sin^{2} \varphi }}{{R^{2} }}\phi_{i} \\ \end{aligned} $$
$$ \begin{aligned} L_{21} & = A_{16} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{(A_{12} + A_{66} )}}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{A_{26} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + (2A_{16} + A_{26} )\frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x}\\ & + (A_{22} + A_{66} )\frac{\sin \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } + A_{26} \frac{{\sin^{2} \varphi }}{{R^{2} }}\phi_{i} \\ \end{aligned} $$
$$ \begin{aligned} L_{22} & = A_{66} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{2A_{26} }}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{A_{22} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + A_{66} \frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x}\\ & - (A_{66} \frac{{\sin^{2} \varphi }}{{R^{2} }} + A_{44} \frac{{\cos^{2} \varphi }}{{R^{2} }})\phi_{i} \\ \end{aligned} $$
$$ L_{23} = (A_{26} + A_{45} )\frac{\cos \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x} + (A_{22} + A_{44} )\frac{\cos \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } + A_{26} \frac{\sin \varphi \cos \varphi }{{R^{2} }}\phi_{i} $$
$$ \begin{aligned} L_{24} & = B_{16} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{(B_{12} + B_{66} )}}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{B_{26} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + (2B_{16} + B_{26} )\frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x}\\ & + (B_{22} + B_{66} )\frac{\sin \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } + \left( {B_{26} \frac{{\sin^{2} \varphi }}{{R^{2} }} + A_{45} \frac{\cos \varphi }{R}} \right)\phi_{i} \\ \end{aligned} $$
$$ \begin{aligned} L_{25} & = B_{66} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{2B_{26} }}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{B_{22} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + B_{66} \frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x}\\ & - \left( {B_{66} \frac{{\sin^{2} \varphi }}{{R^{2} }} - A_{44} \frac{\cos \varphi }{R}} \right)\phi_{i} \\ \end{aligned} $$
$$ L_{31} = - A_{12} \frac{\cos \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x} - A_{26} \frac{\cos \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } - A_{22} \frac{\sin \varphi \cos \varphi }{{R^{2} }}\phi_{i} $$
$$ L_{32} = - (A_{26} + A_{45} )\frac{\cos \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x} - (A_{22} + A_{44} )\frac{\cos \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } + A_{26} \frac{\sin \varphi \cos \varphi }{{R^{2} }}\phi_{i} $$
$$ L_{33} = A_{55} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{2A_{45} }}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{A_{44} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + A_{55} \frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x} - A_{22} \frac{{\cos^{2} \varphi }}{{R^{2} }}\phi_{i} $$
$$ L_{34} = \left( {A_{55} - B_{12} \frac{\cos \varphi }{R}} \right)\frac{{\partial \phi_{i} }}{\partial x} + \left( {\frac{{A_{45} }}{R} - B_{26} \frac{\cos \varphi }{{R^{2} }}} \right)\frac{{\partial \phi_{i} }}{\partial \theta } + \left( {A_{55} \frac{\sin \varphi }{R} - B_{22} \frac{\sin \varphi \cos \varphi }{{R^{2} }}} \right)\phi_{i} $$
$$ L_{35} = \left( {A_{45} - B_{26} \frac{\cos \varphi }{R}} \right)\frac{{\partial \phi_{i} }}{\partial x} + \left( {\frac{{A_{44} }}{R} - B_{22} \frac{\cos \varphi }{{R^{2} }}} \right)\frac{{\partial \phi_{i} }}{\partial \theta } + \left( {A_{45} \frac{\sin \varphi }{R} + B_{26} \frac{\sin \varphi \cos \varphi }{{R^{2} }}} \right)\phi_{i} $$
$$ L_{41} = L_{14} $$
$$ \begin{aligned} L_{42} & = B_{16} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{(B_{12} + B_{66} )}}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{B_{26} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + (B_{16} - B_{26} )\frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x}\\ & - (B_{22} + B_{66} )\frac{\sin \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } + \left( {B_{26} \frac{{\sin^{2} \varphi }}{{R^{2} }} + A_{45} \frac{\cos \varphi }{R}} \right)\phi_{i} \\ \end{aligned} $$
$$ L_{43} = \left( {B_{12} \frac{\cos \varphi }{R} - A_{55} } \right)\frac{{\partial \phi_{i} }}{\partial x} + \left( {B_{26} \frac{\cos \varphi }{{R^{2} }} - \frac{{A_{45} }}{R}} \right)\frac{{\partial \phi_{i} }}{\partial \theta } + (B_{12} - B_{22} )\frac{\sin \varphi \cos \varphi }{{R^{2} }}\phi_{i} $$
$$ L_{44} = D_{11} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{2D_{16} }}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{D_{66} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + D_{11} \frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x} - \left( {D_{22} \frac{{\sin^{2} \varphi }}{{R^{2} }} + A_{55} } \right)\phi_{i} $$
$$ \begin{aligned} L_{45} & = D_{16} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{(D_{12} + D_{66} )}}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{D_{26} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + (D_{16} - D_{26} )\frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x}\\ & - (D_{22} + D_{66} )\frac{\sin \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } + \left( {D_{26} \frac{{\sin^{2} \varphi }}{{R^{2} }} - A_{45} } \right)\phi_{i} \\ \end{aligned} $$
$$ \begin{aligned} L_{51} & = B_{16} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{(B_{12} + B_{66} )}}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{B_{26} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + (2B_{16} + B_{26} )\frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x}\\ & + (B_{22} + B_{66} )\frac{\sin \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } + B_{26} \frac{{\sin^{2} \varphi }}{{R^{2} }}\phi_{i} \\ \end{aligned} $$
$$ L_{52} = L_{25} $$
$$ L_{53} = \left( {B_{26} \frac{\cos \varphi }{R} - A_{45} } \right)\frac{{\partial \phi_{i} }}{\partial x} + \left( {B_{22} \frac{\cos \varphi }{{R^{2} }} - \frac{{A_{44} }}{R}} \right)\frac{{\partial \phi_{i} }}{\partial \theta } + B_{26} \frac{\sin \varphi \cos \varphi }{{R^{2} }}\phi_{i} $$
$$ \begin{aligned} L_{54} & = D_{16} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{(D_{12} + D_{66} )}}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{D_{26} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + (2D_{16} + D_{26} )\frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x}\\ & + (D_{22} + D_{66} )\frac{\sin \varphi }{{R^{2} }}\frac{{\partial \phi_{i} }}{\partial \theta } + \left( {D_{26} \frac{{\sin^{2} \varphi }}{{R^{2} }} - A_{45} } \right)\phi_{i} \\ \end{aligned} $$
$$ L_{55} = D_{66} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} + \frac{{2D_{26} }}{R}\frac{{\partial^{2} \phi_{i} }}{\partial x\partial \theta } + \frac{{D_{22} }}{{R^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial \theta^{2} }} + D_{66} \frac{\sin \varphi }{R}\frac{{\partial \phi_{i} }}{\partial x} - \left( {D_{66} \frac{{\sin^{2} \varphi }}{{R^{2} }} + A_{44} } \right)\phi_{i} $$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kwak, S., Kim, K., Ri, Y. et al. Natural frequency calculation of open laminated conical and cylindrical shells by a meshless method. Eur. Phys. J. Plus 135, 434 (2020). https://doi.org/10.1140/epjp/s13360-020-00438-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-020-00438-0

Search

Navigation