Thermodynamic phase transition for quintessence dyonic anti-de Sitter black holes

Abstract

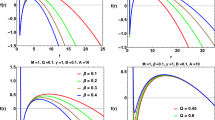
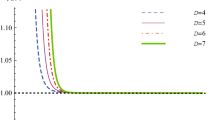
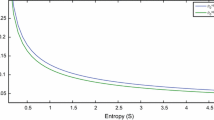
We study the thermodynamics of a dyonic AdS black hole surrounded by quintessence dark energy where negative cosmological constant of AdS space behaves as pressure of the black hole. We choose grand canonical ensemble of the black hole where its magnetic charge $Q_{\mathrm{M}}$ and electric potential $\Phi _{\mathrm{E}}$ are held as constant. Our goal in this work is to study the physical effects of the magnetic charge and electric potential on the thermodynamic phase transition of the black hole in the presence of quintessence dark energy. When barotropic index of the quintessence is $\omega =-\frac{7}{9}$, we obtained that compressibility factor of the black hole reduces to $Z_{\mathrm{c}}=\frac{3}{8}$ which corresponds to the van der Waals fluid. We obtained analogy between the small/large black hole phase transition and liquid/gas phase transition of the van der Waals fluid. Numerical calculations predict that the black hole may born plasma phase which is the fourth different state of the matter which does not appear in the van der Waals fluid.