Skip to main content
SpringerLink
Log in

A new 4-D chaotic hyperjerk system, its synchronization, circuit design and applications in RNG, image encryption and chaos-based steganography

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract.

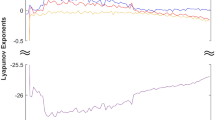
Hyperjerk systems have received significant interest in the literature because of their simple structure and complex dynamical properties. This work presents a new chaotic hyperjerk system having two exponential nonlinearities. Dynamical properties of the chaotic hyperjerk system are discovered through equilibrium point analysis, bifurcation diagram, dissipativity and Lyapunov exponents. Moreover, an adaptive backstepping controller is designed for the synchronization of the chaotic hyperjerk system. Also, a real circuit of the chaotic hyperjerk system has been carried out to show the feasibility of the theoretical hyperjerk model. The chaotic hyperjerk system can also be useful in scientific fields such as Random Number Generators (RNGs), data security, data hiding, etc. In this work, three implementations of the chaotic hyperjerk system, viz. RNG, image encryption and sound steganography have been performed by using complex dynamics characteristics of the system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. S. Vaidyanathan, C. Volos, Advances and Applications in Chaotic Systems (Springer, Berlin, Germany, 2016)

  2. A.T. Azar, S. Vaidyanathan, Advances in Chaos Theory and Intelligent Control (Springer, Berlin, Germany, 2016)

  3. S. Winnings, Introduction to Applied Nonlinear Dynamical Systems and Chaos (Springer, Berlin, German, 2003)

  4. E.N. Lorenz, J. Atmos. Sci. 20, 130 (1963)

    Article  ADS  Google Scholar 

  5. O.E. Rössler, Phys. Lett. A 57, 397 (1976)

    Article  ADS  Google Scholar 

  6. J.C. Sprott, Phys. Rev. 50, 647 (1994)

    Article  ADS  MathSciNet  Google Scholar 

  7. G. Chen, T. Ueda, Int. J. Bifurcat. Chaos 9, 1465 (1999)

    Article  Google Scholar 

  8. H.P.W. Gottlieb, Am. J. Phys. 64, 525 (1996)

    Article  ADS  Google Scholar 

  9. R. Tchitnga, T. Nguazon, P.H.L. Fotso, J.A.C. Gallas, IEEE Trans. Circuits Syst. II: Express Briefs 63, 239 (2016)

    Article  Google Scholar 

  10. J. Heidel, J. Zhang, Int. J. Bifurcat. Chaos 17, 2049 (2007)

    Article  Google Scholar 

  11. S. Ghorui, S.N. Sahasrabudhe, P.S.S. Muryt, A.K. Das, N. Venkatramani, IEEE Trans. Plasma Sci. 28, 235 (2000)

    Article  Google Scholar 

  12. H.G. Enjieu Kadji, J.B. Chabi Orou, R. Yamapi, P. Woafo, Chaos Solitons Fractals 32, 862 (2007)

    Article  ADS  MathSciNet  Google Scholar 

  13. P. Coullet, C. Tresser, A. Arneodo, Phys. Lett. A 72, 268 (1979)

    Article  ADS  MathSciNet  Google Scholar 

  14. J.C. Sprott, Phys. Lett. A 228, 271 (1997)

    Article  ADS  MathSciNet  Google Scholar 

  15. Z. Elhadj, J.C. Sprott, Palest. J. Math. 2, 38 (2013)

    MathSciNet  Google Scholar 

  16. K.E. Chlouverakis, J.C. Sprott, Chaos Solitons Fractals 28, 739 (2006)

    Article  ADS  MathSciNet  Google Scholar 

  17. S.J. Linz, Chaos Solitons Fractals 37, 741 (2008)

    Article  ADS  MathSciNet  Google Scholar 

  18. S. Vaidyanathan, C. Volos, V.T. Pham, K. Madhavan, Arch. Control Sci. 25, 135 (2015)

    MathSciNet  Google Scholar 

  19. S. Vaidyanathan, Int. J. Control Theory Appl. 9, 257 (2016)

    Google Scholar 

  20. S. Vaidyanathan, Arch. Control Sci. 26, 311 (2016)

    Google Scholar 

  21. S. Vaidyanathan, A. Sambas, M. Mamat, M. Sanjaya WS, Int. J. Model. Identif. Control 26, 153 (2017)

    Article  Google Scholar 

  22. X. Wang, S. Vaidyanathan, C. Volos, V.T. Pham, T. Kapitaniak, Nonlinear Dyn. 89, 1673 (2017)

    Article  Google Scholar 

  23. A. Sambas, S. Vaidyanathan, M. Mamat, M. Sanjaya WS, R.P. Prastio, Int. J. Control Theory Appl. 9, 141 (2016)

    Google Scholar 

  24. Z.T. Njitacke, J. Kengne, L. Kamdjeu Kengne, Chaos Solitons Fractals 105, 77 (2017)

    Article  ADS  MathSciNet  Google Scholar 

  25. A.S. Mansingka, M. Affan Zidan, M.L. Barakat, A.G. Radwan, K.N. Salama, Microelectron. J. 44, 744 (2013)

    Article  Google Scholar 

  26. R.A. El-Nabulsi, Int. J. Non-Linear Mech. 93, 65 (2017)

    Article  ADS  Google Scholar 

  27. H. Bao, N. Wang, B. Bao, M. Chen, P. Jin, G. Wang, Commun. Nonlinear Sci. Numer. Simul. 57, 264 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  28. F.Y. Dalkiran, J.C. Sprott, Int. J. Bifurcat. Chaos 26, 1650189 (2016)

    Article  Google Scholar 

  29. A. Wolf, J.B. Swift, H.L. Swinney, J.A. Vastano, Physica D 16, 285 (1985)

    Article  ADS  MathSciNet  Google Scholar 

  30. P. Frederickson, J. Kaplan, E. Yorke, J. Yorke, J. Differ. Equ. 49, 185 (1983)

    Article  ADS  Google Scholar 

  31. H.K. Khalil, Nonlinear Systems (Prentice Hall, New Jersey, USA, 2002)

  32. A statistical test suite for random and pseudo RNGs for cryptographic applications, NIST-800-22 (National Institute of Standards and Techniques, 2001) http://csrc.nist.gov/publications/nistpubs/800-22/sp-800-22-051501.pdf

  33. P.K. Narendra, P. Vinod, K.S. Krishan, Image Vision Comput. 24, 926 (2006)

    Article  Google Scholar 

  34. E. Biham, A. Shamir, J. Cryptol. 4, 3 (1991)

    Article  Google Scholar 

  35. Y. Wang, K.W. Wong, X. Liao, T. Xiang, G. Chen, Chaos Solitons Fractals 41, 1773 (2009)

    Article  ADS  Google Scholar 

  36. C.E. Shannon, Bell Syst. Tech. J. 28, 656 (1948)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Vel Tech University, Research and Development Centre, Chennai-600 062, Tamil Nadu, India

    S. Vaidyanathan

  2. Department of Electrical and Electronics Engineering, Faculty of Technology, Sakarya University, 54187, Sakarya, Turkey

    A. Akgul & S. Kaçar

  3. Department of Computer Engineering, Faculty of Technology, Sakarya University, 54187, Sakarya, Turkey

    U. Çavuşoğlu

Authors
  1. S. Vaidyanathan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Akgul
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. Kaçar
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. U. Çavuşoğlu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Vaidyanathan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vaidyanathan, S., Akgul, A., Kaçar, S. et al. A new 4-D chaotic hyperjerk system, its synchronization, circuit design and applications in RNG, image encryption and chaos-based steganography. Eur. Phys. J. Plus 133, 46 (2018). https://doi.org/10.1140/epjp/i2018-11872-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/i2018-11872-8

Search

Navigation