Abstract.
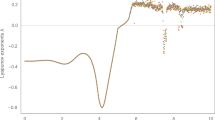
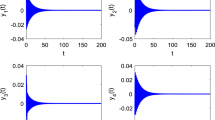
In this paper, the fractional-order simplest memristor-based chaotic circuit is investigated based on the novel conformable Adomian decomposition method (CADM). Dynamics of this circuit is analyzed by employing bifurcation diagram, Lyapunov exponent spectrum, Poincaré section and other methods. The result shows that it has rich dynamical behaviors and we found the minimum order of this system for generating chaos is 1.08. To implement the system in digital circuit, the CADM iteration results with different items are compared to balance the speed and accuracy, and the suitable items are chosen for further application. Finally, DSP implementation of the system verifies the effectiveness of the solution algorithm.
Similar content being viewed by others
References
S. Wang, B. Yan, Nonlinear Dyn. 73, 611 (2013)
S. Das, Observation of Fractional Calculus in Physical System Description (Springer, Berlin, Heidelberg, 2011) pp. 101--156
V.E. Tarasov, Int. J. Mod. Phys. B 27, 1 (2015)
L. Liu, D. Liang, C. Liu, Nonlinear Dyn. 69, 1929 (2012)
L. Godinho, J. Weberszpil, A. Helayel-Neto, Chaos, Solitons Fractals 45, 765 (2012)
A. Carpinteri, F.M. Ed, Fractals and Fractional Calculus in Continuum Mechanics (Springer-Verlag, Vienna, 1997)
R. Khalil, M. Al Horani, A. Yousef, M. Sababheh, J. Comput. Appl. Math. 264, 65 (2014)
T. Abdeljawad, J. Comput. Appl. Math. 279, 57 (2014)
S. He, K. Sun, X. Mei, B. Yan, S. Xu, Eur. Phys. J. Plus 132, 36 (2017)
O.S. Iyiola, O. Tasbozan, A.K. Çesiz, Chaos, Solitons Fractals 97, 1 (2016)
W.S. Chung, J. Comput. Appl. Math. 290, 150 (2015)
A. Charef, H.H. Sun, Y.Y. Tsao, B. Onaral, IEEE Trans. Autom. Control 37, 1465 (1992)
H.H. Sun, A.A. Abdelwahab, B. Onaral, IEEE Trans. Autom. Control 29, 441 (1984)
G. Adomian, Comput. Math. Appl. 22, 101 (1991)
S. He, K. Sun, H. Wang, Acta Phys. Sin. 63, 030502 (2014)
L.O. Chua, IEEE Trans. Circ. Theory 18, 507 (1971)
D.B. Strukov, G.S. Snider, D.R. Stewart, R.S. Williams, Nature 453, 80 (2008)
B. Bao, Z. Ma, J. Xu, Z. Liu, Q. Xu, Int. J. Bifurc. Chaos 21, 2629 (2011)
J. Sun, Y. Shen, Q. Yin, C. Xu, Chaos 23, 013140 (2013)
J. Ruan, K. Sun, J. Mou, Acta Phys. Sin. 65, 190502 (2016)
F. Yuan, G. Wang, X. Wang, Chaos 26, 073107 (2016)
B. Muthswamy, L.O. Chua, Int. J. Bifurc. Chaos 20, 1567 (2010)
D. Cafagna, G. Grassi, Nonlinear Dyn. 70, 1185 (2012)
K. Sun, X. Liu, C. Zhu, Chin. Phys. B 19, 110510 (2010)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Ruan, J., Sun, K., Mou, J. et al. Fractional-order simplest memristor-based chaotic circuit with new derivative. Eur. Phys. J. Plus 133, 3 (2018). https://doi.org/10.1140/epjp/i2018-11828-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjp/i2018-11828-0