Skip to main content
SpringerLink
Log in

Axisymmetric Stokes flow past a composite spheroidal shell of immiscible fluids

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract.

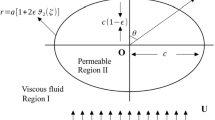
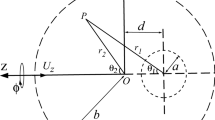
We study the flow of an incompressible Newtonian fluid past a composite spheroidal shell whose shape deviates slightly from that of a sphere. A composite particle referred to in this paper is a spheroidal liquid core covered with a porous layer. The Brinkman equation is used for the flow inside the porous medium and the Stokes equation is used for the flow in the fluid region. We assume that the external and internal viscous fluids are immiscible and the viscosity of the porous medium is different than the viscosity of pure liquid. The Ochoa-Tapia and Whitaker’s stress jump boundary condition for tangential stress is applied on the porous-fluid interface. Velocity and pressure distributions are found and the drag force acting on the spheroidal shell is evaluated. The analytical solution is obtained by dividing the flow into three regions. Both type of spheroids, oblate and prolate are considered. Numerical results of the normalized hydrodynamic drag force acting on the spheroidal shell are tabulated and represented graphically for different values of the parameters characterizing the stress jump coefficient, separation parameter, permeability, deformation parameter, and viscosity ratios. The analysis of the flow pattern is done by plotting streamlines and several renowned cases are deduced.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. J.S. Hadamard, C. R. Acad. Sci. Paris 152, 1735 (1911)

    Google Scholar 

  2. W. Rybczynski, Bull. Acad. Sci. Cracovie, Ser. A 40, 40 (1911)

    Google Scholar 

  3. G.G. Stokes, Trans. Cambridge Philos. Soc. 9, 8 (1851)

    ADS  Google Scholar 

  4. J. Happel, H. Brenner, Low Reynolds Number Hydrodynamics (Prentice-Hall, Englewood Cliffs, NJ, 1965)

  5. E. Bart, Chem. Eng. Sci. 23, 193 (1968)

    Article  Google Scholar 

  6. G. Hetsroni, S. Haber, Rheol. Acta 9, 488 (1970)

    Article  Google Scholar 

  7. E. Wacholder, D. Weihs, Chem. Eng. Sci. 27, 1817 (1972)

    Article  Google Scholar 

  8. T.C. Lee, H.J. Keh, Eur. J. Mech. B: Fluids 34, 97 (2012)

    Article  ADS  MathSciNet  Google Scholar 

  9. D. Choudhuri, B. Sri Padmavati, Appl. Math. Comput. 243, 644 (2014)

    MathSciNet  Google Scholar 

  10. R. Niefer, P.N. Kaloni, J. Eng. Math. 14, 107 (1980)

    Article  Google Scholar 

  11. H. Ramkissoon, Z. Angew. Math. Mech. 65, 635 (1985)

    Article  MathSciNet  Google Scholar 

  12. H. Ramkissoon, S.R. Majumdar, Z. Angew. Math. Mech. 68, 155 (1988)

    Article  MathSciNet  Google Scholar 

  13. E.I. Saad, Meccanica 47, 2055 (2012)

    Article  MathSciNet  Google Scholar 

  14. M. Krishna Prasad, M. Kaur, Sadhana 41, 1463 (2016)

    Google Scholar 

  15. D.D. Joseph, L.N. Tao, Z. Angew. Math. Mech. 44, 361 (1964)

    Article  Google Scholar 

  16. D.N. Sutherland, C.T. Tan, Chem. Eng. Sci. 25, 1948 (1970)

    Article  Google Scholar 

  17. H.C. Brinkman, Appl. Sci. Res. A 1, 27 (1947)

    Article  Google Scholar 

  18. P. Debye, A.M. Bueche, J. Chem. Phys. 16, 573 (1948)

    Article  ADS  Google Scholar 

  19. G. Ooms, P.F. Mijnlieff, H.L. Beckers, J. Chem. Phys. 53, 4123 (1970)

    Article  ADS  Google Scholar 

  20. G. Neale, N. Epstein, W. Nader, Chem. Eng. Sci. 28, 1865 (1973)

    Article  Google Scholar 

  21. Y. Qin, P.N. Kaloni, J. Eng. Math. 22, 177 (1988)

    Article  Google Scholar 

  22. B.S. Bhatt, N.C. Sacheti, J. Phys. D.: Appl. Phys. 27, 37 (1994)

    Article  ADS  Google Scholar 

  23. D. Srinivasacharya, Z. Angew. Math. Mech. 83, 499 (2003)

    Article  Google Scholar 

  24. T. Zlatanovski, Q. J. Mech. Appl. Math. 52, 111 (1999)

    Article  MathSciNet  Google Scholar 

  25. H.J. Keh, J. Chou, Chem. Eng. Sci. 59, 407 (2004)

    Article  Google Scholar 

  26. H.J. Keh, Y.S. Lu, J. Fluids Struct. 20, 735 (2005)

    Article  ADS  Google Scholar 

  27. E.I. Saad, Can. J. Phys. 88, 689 (2010)

    Article  ADS  Google Scholar 

  28. J.A. Ochoa-Tapia, S. Whitaker, Int. J. Heat Mass Transfer 38, 2635 (1995)

    Article  Google Scholar 

  29. J.A. Ochoa-Tapia, S. Whitaker, Int. J. Heat Mass Transfer 38, 2647 (1995)

    Article  Google Scholar 

  30. A.V. Kuznetsov, Appl. Sci. Res. 56, 53 (1996)

    Article  ADS  Google Scholar 

  31. A. Bhattacharyya, G.P. Raja Sekhar, Z. Angew. Math. Phys. 56, 475 (2005)

    Article  MathSciNet  Google Scholar 

  32. P.K. Yadav, A. Tiwari, S. Deo, A. Filippov, S. Vasin, Acta Mech. 215, 193 (2010)

    Article  Google Scholar 

  33. J. Prakash, G.P. Raja Sekhar, M. Kohr, Z. Angew. Math. Phys. 62, 1027 (2011)

    Article  MathSciNet  Google Scholar 

  34. D. Srinivasacharya, M. Krishna Prasad, Z. Angew. Math. Mech. 91, 824 (2011)

    Article  Google Scholar 

  35. D. Srinivasacharya, M. Krishna Prasad, ANZIAM J. 52, 289 (2011)

    Article  MathSciNet  Google Scholar 

  36. D. Srinivasacharya, M. Krishna Prasad, Eur. Phys. J. Plus. 128, 9 (2013)

    Article  Google Scholar 

  37. E.I. Saad, Meccanica 48, 1747 (2013)

    Article  MathSciNet  Google Scholar 

  38. E.A. Ashmawy, Eur. Phys. J. Plus 130, 163 (2015)

    Article  Google Scholar 

  39. E.A. Ashmawy, Eur. J. Mech. B/Fluids 50, 147 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  40. S.I. Vasin, T.V. Kharitonova, Colloid J. 73, 18 (2011)

    Article  Google Scholar 

  41. S.I. Vasin, T.V. Kharitonova, Colloid J. 73, 297 (2011)

    Article  Google Scholar 

  42. C. Pozrikidis, Modeling and Simulation of Capsules and Biological Cells (Chapman & Hall/CRC, New York, 2003)

  43. B.R. Jaiswal, B.R. Gupta, J. Appl. Fluid Mech. 8, 339 (2015)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, National Institute of Technology, Raipur-492010, Chhattisgarh, India

    M. Krishna Prasad & G. Manpreet Kaur

Authors
  1. M. Krishna Prasad
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. G. Manpreet Kaur
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Krishna Prasad.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Krishna Prasad, M., Manpreet Kaur, G. Axisymmetric Stokes flow past a composite spheroidal shell of immiscible fluids. Eur. Phys. J. Plus 132, 469 (2017). https://doi.org/10.1140/epjp/i2017-11744-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/i2017-11744-9

Search

Navigation