Abstract.
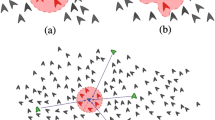
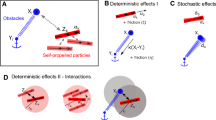
In our work we have studied a two-dimensional suspension of finite-size Vicsek hard disks, whose time evolution follows an event-driven dynamics between subsequent time steps. Having compared its collective behaviour with the one expected for a system of scalar Vicsek point-like particles, we have analysed the effect of considering two possible bouncing rules between the disks: a Vicsek-like rule and a pseudo-elastic one, focusing on the order-disorder transition. Next, we have added to the two-dimensional suspension of hard-disk Vicsek particles disk-like passive obstacles of two types: either fixed in space or moving according to the same event-driven dynamics. We have performed a detailed analysis of the particles’ collective behaviour observed for both fixed and moving obstacles. In the fixed obstacles case, we have observed formation of clusters at low noise, in agreement with previous studies. When using moving passive obstacles, we found that that order of active particles is better destroyed as the drag of obstacles increases. In the no drag limit an interesting result was found: introduction of low drag passive particles can lead in some cases to a more ordered state of active flocking particles than what they show in bulk.
Graphical abstract
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
S. Frank, Brownian Agents and Active Particles: Collective Dynamics in the Natural and Social Sciences (Springer, Berlin, 2003)
C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe, G. Volpe, Rev. Mod. Phys. 88, 045006 (2016)
M.C. Marchetti, J.-F. Joanny, S. Ramaswamy, T.B. Liverpool, J. Prost, M. Rao, R.A. Simha, Rev. Mod. Phys. 85, 1143 (2013)
G.I. Menon, Active matter, in Rheology of Complex Fluids (Springer, 2010) pp. 193--218
S.A. Mallory, C. Valeriani, A. Cacciuto, Annu. Rev. Phys. Chem. 69, 59 (2018)
S. Ramaswamy, Annu. Rev. Condens. Matter Phys. 1, 323 (2010)
M.E. Cates, J. Tailleur, Annu. Rev. Condens. Matter Phys. 6, 219 (2015)
J. Toner, Y. Tu, S. Ramaswamy, Ann. Phys. 318, 170 (2005)
M.C. Marchetti, J.-F. Joanny, S. Ramaswamy, T.B. Liverpool, J. Prost, M. Rao, R.A. Simha, Rev. Mod. Phys. 85, 1143 (2013)
T. Vicsek, A. Zafeiris, Phys. Rep. 517, 71 (2012)
M. Aldana, V. Dossetti, C. Huepe, V. Kenkre, H. Larralde, Phys. Rev. Lett. 98, 095702 (2007)
J. Deseigne, O. Dauchot, H. Chaté, Phys. Rev. Lett. 105, 098001 (2010)
C.A. Weber, T. Hanke, J. Deseigne, S. Lé, Phys. Rev. Lett. 110, 208001 (2013)
G. Gré, Phys. Rev. Lett. 92, 025702 (2004)
H. Chaté, Phys. Rev. E 77, 046113 (2008)
F. Ginelli, Eur. Phys. J. ST 225, 2099 (2016)
T. Vicsek, A. Cziró, Phys. Rev. Lett. 75, 1226 (1995)
J. Gautrais, F. Ginelli, R. Fournier, S. Blanco, M. Soria, H. Chaté, Plos Comput. Biol. 8, e1002678 (2012)
G. Gré, Phys. Rev. E 64, 011902 (2001)
H. Chaté, Eur. Phys. J. B 64, 451 (2008)
C. Valeriani, M. Li, J. Novosel, J. Arlt, D. Marenduzzo, Soft Matter 7, 5228 (2011)
T. Schilling, T. Voigtmann, J. Chem. Phys. 147, 214905 (2017)
E. Marsden, C. Valeriani, I. Sullivan, M. Cates, D. Marenduzzo, Soft Matter 10, 157 (2014)
O. Pohl, H. Stark, Phys. Rev. Lett. 112, 238303 (2014)
O. Chepizhko, F. Peruani, Phys. Rev. Lett. 111, 160604 (2013)
O. Chepizhko, F. Peruani, Eur. Phys. J. ST 224, 1287 (2015)
D. Yllanes, M. Leoni, M. Marchetti, New J. Phys. 19, 103026 (2017)
B.J. Alder, T.E. Wainwright, J. Chem. Phys. 31, 459 (1959)
M.N. Bannerman, S. Strobl, A. Formella, T. Pöschel, Comput. Part. Mech. 1, 191 (2014)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Martinez, R., Alarcon, F., Rodriguez, D.R. et al. Collective behavior of Vicsek particles without and with obstacles⋆. Eur. Phys. J. E 41, 91 (2018). https://doi.org/10.1140/epje/i2018-11706-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epje/i2018-11706-8