Skip to main content
SpringerLink
Log in

Stability of a gravity-driven thin electrolyte film flowing over a heated substrate

  • Regular Article
  • Published:
The European Physical Journal E Aims and scope Submit manuscript

Abstract.

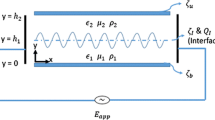
The stability of a thin electrolyte liquid film driven by gravity over a vertical substrate is presented. A film thickness evolution equation is derived and solved numerically. The substrate is non-uniformly heated from below which is modeled by imposing a temperature profile at the liquid-solid interface. The electrohydrodynamics is included in the model with Maxwell’s stress tensor. The governing flow and energy equations are simplified using the lubrication approximation. The Poisson-Boltzmann equation with Debye-Hückel approximation is used for the potential which is generated inside the film due to a charged layer at the liquid-solid interface. The positive temperature gradient at the substrate leads to the formation of a thermocapillary ridge due to an opposing Marangoni stress. This thermocapillary ridge becomes unstable beyond critical parameters related to Marangoni stress and convective energy loss at the free surface. The electroosmotic flow has no effect on the base profile of the film, but enhances its instability. A parameter space is presented delineating the stable and unstable regimes for the film dynamics.

Graphical abstract

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. L. Fu, J. Lin, R. Yang, J. Colloid Interface Sci. 258, 266 (2002)

    Article  Google Scholar 

  2. A. Brask, G. Goranović, H. Bruus, Tech. Proc. Nanotechnol. 1, 190 (2003)

    Google Scholar 

  3. B.J. Kirby, E.F. Hasselbrink, Electrophoresis 25, 187 (2004)

    Article  Google Scholar 

  4. D.R. Reyes, D. Iossifidis, P. Auroux, A. Manz, Anal. Chem. 74, 2623 (2002)

    Article  Google Scholar 

  5. J. Melcher, G. Taylor, Annu. Rev. Fluid Mech. 1, 111 (1969)

    Article  ADS  Google Scholar 

  6. D.A. Saville, Annu. Rev. Fluid Mech. 29, 27 (1997)

    Article  ADS  MathSciNet  Google Scholar 

  7. C.L. Brucham, D.A. Saville, J. Fluid Mech. 452, 163 (2002)

    ADS  Google Scholar 

  8. J.L. Anderson, Annu. Rev. Fluid Mech. 21, 61 (1989)

    Article  ADS  MathSciNet  Google Scholar 

  9. T.B. Benjamin, J. Fluid Mech. 2, 554 (1957)

    Article  ADS  MathSciNet  Google Scholar 

  10. A. Oron, S.H. Davis, S.G. Bankoff, Rev. Mod. Phys. 69, 931 (1997)

    Article  ADS  Google Scholar 

  11. S.H. Davis, Annu. Rev. Fluid Mech. 19, 403 (1987)

    Article  ADS  Google Scholar 

  12. B. Ramaswamy, S. Krishnamoorthy, S.W. Joo, J. Comput. Phys. 131, 70 (1997)

    Article  ADS  Google Scholar 

  13. V. Ajaev, J. Colloid Interface Sci. 280, 165 (2004)

    Article  Google Scholar 

  14. N. Tiwari, J.M. Davis, Phys. Fluids 21, 022105 (2009)

    Article  ADS  Google Scholar 

  15. L. Ren, W. Qu, D. Li, Int. J. Heat Mass Transfer 44, 3125 (2001)

    Article  Google Scholar 

  16. Y. Gu, D. Li, J. Colloid Interface Sci. 226, 328 (2000)

    Article  Google Scholar 

  17. J.S.H. Lee, D. Li, Microfluid. Nanofluid. 2, 361 (2006)

    Article  Google Scholar 

  18. S. Joo, J. Mech. Sci. Technol. 22, 382 (2007)

    Article  Google Scholar 

  19. S. Joo, Microfluid. Nanofluid. 5, 417 (2008)

    Article  Google Scholar 

  20. I.M.R. Sadiq, S.W. Joo, Micrograv. Sci. Technol. 21, 331 (2009)

    Article  ADS  Google Scholar 

  21. B. Ray, P.D.S. Reddy, D. Bandyopadhyay, S.W. Joo, A. Sharma, S. Qian, G. Biswas, Electrophoresis 32, 3257 (2011)

    Article  Google Scholar 

  22. B. Ray, D. Bandyopadhyay, A. Sharma, S.W. Joo, S. Qian, G. Biswas, Microfluid. Nanofluid. 15, 19 (2013)

    Article  Google Scholar 

  23. B. Ray, P.D.S. Reddy, D. Bandyopadhyay, S.W. Joo, A. Sharma, S. Qian, G. Biswas, Theor. Comput. Fluid Dyn. 26, 311 (2012)

    Article  Google Scholar 

  24. O.A. Kabov, in Proceedings of the 1st Russian National Conference on Heat Transfer, Vol. 6 (1994) p. 90

  25. N. Tiwari, Z. Mester, J.M. Davis, Phys. Rev. E 76, 056306 (2007)

    Article  ADS  Google Scholar 

  26. J.S. Newman, K.E. Thomas-Alyea, Electrochemical Systems (John Wiley and Sons, Hoboken, NJ, 2004)

  27. B. Fornberg, Math. Comput. 51, 699 (1988)

    Article  Google Scholar 

  28. N. Tiwari, A. Awasthi, J.M. Davis, Phys. Fluids 26, 042105 (2014)

    Article  ADS  Google Scholar 

  29. B.J. Kirby, Micro- and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices (Cambridge University Press, New York, 2010)

  30. A.M. Frank, O.A. Kabov, Phys. Fluids 18, 032107 (2006)

    Article  ADS  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Chemical Engineering, Indian Institute of Technology Kanpur, 208016, Kanpur, India

    Tara Chand Kumawat, Ajit Vikram & Naveen Tiwari

Authors
  1. Tara Chand Kumawat
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ajit Vikram
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Naveen Tiwari
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Naveen Tiwari.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumawat, T.C., Vikram, A. & Tiwari, N. Stability of a gravity-driven thin electrolyte film flowing over a heated substrate. Eur. Phys. J. E 40, 52 (2017). https://doi.org/10.1140/epje/i2017-11540-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epje/i2017-11540-6

Keywords

Search

Navigation