Skip to main content
SpringerLink
Log in

Wehrl entropy of entangled oscillators from the Segal–Bargmann formalism

  • Regular Article – Quantum Optics
  • Published:
The European Physical Journal D Aims and scope Submit manuscript

Abstract

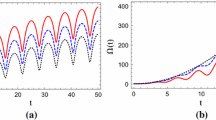
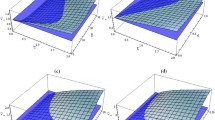
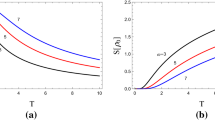
In this manuscript, we study the Wehrl entropy of entangled oscillators. This semiclassical entropy associated with the phase-space description of quantum mechanics can be used for formulating uncertainty relations and for a quantification of entanglement. We focus on a system of two coupled oscillators described within its Segal–Bargmann space. This Hilbert space of holomorphic functions integrable with respect to a given Gaussian-like measure is particularly convenient to deal with harmonic oscillators. Indeed, the Stone–von Neumann theorem allows us to work in this space in a full correspondence with the ladder operators formalism. In addition, the Husimi pseudoprobability distribution is directly computed within the Segal–Bargmann formalism. Once we obtain the Husimi function, we analyse the Wehrl entropy and mutual information.

Graphic abstract

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Data Availability

This manuscript has no associated data or the data will not be deposited. Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.

Notes

  1. This expression holds as long as each term is finite. Clearly, this is our case for finite coupling \(\eta \).

References

  1. P. Dirac, Principles of Quantum Mechanics (Oxford University Press, Oxford, England, 1982)

    Google Scholar 

  2. C. Zachos, D. Fairlie, T. Curtright, Quantum Mechanics in Phase Space An Overview with Selected Papers (World Scientific, Singapore, 2005)

  3. E. Wigner, On the quantum correction for thermodynamic equilibrium. Phys. Rev. 40, 749–759 (1932). https://doi.org/10.1103/PhysRev.40.749

    Article  ADS  MATH  Google Scholar 

  4. E. Weyl, Quantenmechanik und gruppentheorie. Z. Phys. 46, 1–46 (1927)

    Article  ADS  MATH  Google Scholar 

  5. K. Husimi, Some formal properties of the density matrix. Proc. Physico-Math. Soc. Jpn. 3rd Ser. 22(4), 64–314 (1940). https://doi.org/10.11429/ppmsj1919.22.4_264

    Article  MATH  Google Scholar 

  6. H.-W. Lee, Theory and application of the quantum phase-space distribution functions. Phys. Rep. 259(3), 147–211 (1995). https://doi.org/10.1016/0370-1573(95)00007-4

    Article  ADS  MathSciNet  Google Scholar 

  7. I.E. Segal, Mathematical Problems of Relativistic Physics: With an Appendix on Group Representations in Hilbert Space (American Mathematical Society, Providence, RI, 1967)

    Google Scholar 

  8. V. Bargmann, On a Hilbert space of analytic functions and an associated integral transform part I. Commun. Pure Appl. Math. 14(3), 187–214 (1961). https://doi.org/10.1002/cpa.3160140303

    Article  MATH  Google Scholar 

  9. B. Hall, Holomorphic methods in analysis and mathematical physics. Contemp. Math. (2000). https://doi.org/10.1090/conm/260/04156

    Article  MATH  Google Scholar 

  10. R. Horodecki, P. Horodecki, M. Horodecki, K. Horodecki, Quantum entanglement. Rev. Mod. Phys. 81(2), 865–942 (2009). https://doi.org/10.1103/revmodphys.81.865

    Article  ADS  MathSciNet  MATH  Google Scholar 

  11. A. Einstein, B. Podolsky, N. Rosen, Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780 (1935). https://doi.org/10.1103/PhysRev.47.777

    Article  ADS  MATH  Google Scholar 

  12. J.S. Bell, On the Einstein Podolsky Rosen paradox. Phys. Phys. Fiz. 1, 195–200 (1964). https://doi.org/10.1103/PhysicsPhysiqueFizika.1.195

    Article  MathSciNet  Google Scholar 

  13. D.N. Makarov, Coupled harmonic oscillators and their quantum entanglement. Phys. Rev. E 97, 042203 (2018). https://doi.org/10.1103/PhysRevE.97.042203

    Article  ADS  Google Scholar 

  14. V. Vedral, Entanglement in the second quantization formalism. Central Eur. J. Phys. 1, 289–306 (2003) arXiv:quant-ph/0302040. https://doi.org/10.2478/BF02476298

  15. D. Han, Y. Kim, M. Noz, Illustrative example of Feynman’s rest of the universe. Am. J. Phys. 67(1999). https://doi.org/10.1119/1.19192

  16. S.S. Mizrahi, M.A. Marchiolli, Pseudo-diffusion equation and information entropy of squeezed-coherent states. Phys. A Stat. Mech. Appl. 199(1), 96–115 (1993). https://doi.org/10.1016/0378-4371(93)90100-I

    Article  MathSciNet  Google Scholar 

  17. M.A. Marchiolli, E.C. Silva, D. Galetti, Quasiprobability distribution functions for finite-dimensional discrete phase spaces: spin-tunneling effects in a toy model. Phys. Rev. A 79, 022114 (2009). https://doi.org/10.1103/PhysRevA.79.022114

    Article  ADS  Google Scholar 

  18. J. Klauder, B. Skagerstam, Coherent states. World Scientific (1985). https://doi.org/10.1142/0096. https://www.worldscientific.com/doi/abs/10.1142/0096

  19. N.N. Bogoljubov, V.V. Tolmachov, D.V. Širkov, A new method in the theory of superconductivity. Fortschr. Phys. 6(11–12), 605–682 (1958). https://doi.org/10.1002/prop.19580061102

    Article  Google Scholar 

  20. P. Shanta, S. Chaturvedi, V. Srinivasan, G.S. Agarwal, C.L. Mehta, Unified approach to multiphoton coherent states. Phys. Rev. Lett. 72, 1447–1450 (1994). https://doi.org/10.1103/PhysRevLett.72.1447

    Article  ADS  Google Scholar 

  21. K. Takahashi, Wigner and Husimi functions in quantum mechanics. J. Phys. Soc. Jpn. 55(3), 762–779 (1986). https://doi.org/10.1143/JPSJ.55.762

    Article  ADS  MathSciNet  Google Scholar 

  22. A. Wehrl, General properties of entropy. Rev. Mod. Phys. 50, 221–260 (1978). https://doi.org/10.1103/RevModPhys.50.221

    Article  ADS  MathSciNet  MATH  Google Scholar 

  23. D. Janzing, in Entropy of Entanglement, ed. by D. Greenberger, K. Hentschel, F. Weinert (Springer, Berlin, Heidelberg, 2009), pp. 205–209. https://doi.org/10.1007/978-3-540-70626-7_66

  24. S. Floerchinger, T. Haas, H. Müller-Groeling, Wehrl entropy, entropic uncertainty relations, and entanglement. Phys. Rev. A (2021). https://doi.org/10.1103/physreva.103.062222

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

We are grateful to Ángel Rivas for useful discussions. This work was partially supported by the MICINN (Ministerio de Ciencia e Innovación, Spain) project PID2019-107394GB-I00/AEI/10.13039/501100011033 (AEI/FEDER, UE). This article/publication is based upon work from COST Action COSMIC WISPers CA21106, supported by COST (European Cooperation in Science and Technology). JARC acknowledges support by Institut Pascal at Université Paris-Saclay during the Paris-Saclay Astroparticle Symposium 2022, with the support of the P2IO Laboratory of Excellence (program “Investissements d’avenir” ANR-11-IDEX-0003-01 Paris-Saclay and ANR-10-LABX-0038), the P2I axis of the Graduate School of Physics of Université Paris-Saclay, as well as IJCLab, CEA, APPEC, IAS, OSUPS, and the IN2P3 master project UCMN.

Author information

Authors and Affiliations

  1. Departamento de Física Teórica, Facultad de Ciencias Físicas, Universidad Complutense de Madrid, Plaza de Ciencias 1, 28040, Madrid, Spain

    David Alonso-López, Jose A. R. Cembranos, David Díaz-Guerra & Andrés Mínguez-Sánchez

  2. Institute of Particle and Cosmos Physics (IPARCOS), Facultad de Ciencias Físicas, Universidad Complutense de Madrid, Plaza de Ciencias 1, 28040, Madrid, Spain

    Jose A. R. Cembranos

Authors
  1. David Alonso-López
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jose A. R. Cembranos
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. David Díaz-Guerra
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Andrés Mínguez-Sánchez
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors contributed equally to this manuscript.

Corresponding author

Correspondence to David Díaz-Guerra.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Alonso-López, D., Cembranos, J.A.R., Díaz-Guerra, D. et al. Wehrl entropy of entangled oscillators from the Segal–Bargmann formalism. Eur. Phys. J. D 77, 43 (2023). https://doi.org/10.1140/epjd/s10053-023-00629-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjd/s10053-023-00629-1

Search

Navigation