Abstract
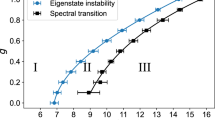
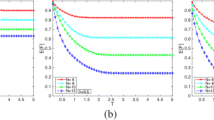
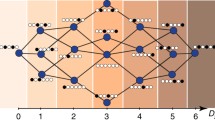
A recent experiment by Bordia et al. [P. Bordia et al., Nat. Phys. 13, 5 (2017)] has demonstrated that periodically modulating the potential of a localised many-body quantum system described by the Aubry-André Hamiltonian with on-site interactions can lead to a many-body localisation-delocalisation transition, provided the modulation amplitude is big enough. Here, we consider the noninteracting counterpart of that model in order to explore its phase diagram as a function of the strength of the disordered potential, the driving frequency and its amplitude. We will first of all mimic the experimental procedure of Bordia et al. and use the even-odd sites imbalance as a parameter in order to discern between different phases. Then we compute the Floquet eigenstates and relate the localisation-delocalisation transition to their IPR. Both these approaches show that the delocalisation transition occurs for frequencies that are low compared to the bandwidth of the time independent model. Moreover, in agreement with [P. Bordia et al., Nat. Phys. 13, 5 (2017)] there is an amplitude threshold below which no delocalisation transition occurs. We estimate both the critical values for the frequency and the amplitude.
Graphical abstract

Article PDF
Similar content being viewed by others
References
J.H. Shirley, Phys. Rev. 138, B979 (1965)
H. Sambe, Phys. Rev. A 7, 2203 (1973)
A. Eckardt, Rev. Mod. Phys. 89, 011004 (2017)
D.H. Dunlap, V.M. Kenkre, Phys. Rev. B 34, 3625 (1986)
M. Holthaus, Phys. Rev. Lett. 69, 351 (1992)
M. Grifoni, P. Hänggi, Phys. Rep. 304, 229 (1998)
H. Lignier, C. Sias, D. Ciampini, Y. Singh, A. Zenesini, O. Morsch, E. Arimondo, Phys. Rev. Lett. 99, 220403 (2007)
J. Zak, Phys. Rev. Lett. 71, 2623 (1993)
A. Eckardt, M. Holthaus, Europhys. Lett. 80, 50004 (2007)
A. Eckardt, C. Weiss, M. Holthaus, Phys. Rev. Lett. 95, 260404 (2005)
A. Zenesini, H. Lignier, D. Ciampini, O. Morsch, E. Arimondo, Phys. Rev. Lett. 102, 100403 (2009)
G. Jotzu, M. Messer, R. Desbuquois, M. Lebrat, T. Uehlinger, D. Greif, T. Esslinger, Nature 515, 237 (2014)
M. Aidelsburger, M. Atala, S. Nascimbène, S. Trotzky, Y-A. Chen, I. Bloch, Phys. Rev. Lett. 107, 255301 (2011)
J. Struck, C. Ölschläger, M. Weinberg, P. Hauke, J. Simonet, A. Eckardt, M. Lewenstein, K. Sengstock, P. Windpassinger, Phys. Rev. Lett. 108, 225304 (2012)
N. Goldman, J. Dalibard, Phys. Rev. X 4, 031027 (2014)
P. Bordia, H. Luschen, U. Schneider, M. Knap, I. Bloch, Nat. Phys. 13, 5 (2017)
S. Aubry, G. André, Ann. Israel Phys. Soc. 3, 18 (1980)
V. Khemani, A. Lazarides, R. Moessner, S.L. Sondhi, Phys. Rev. Lett. 116, 250401 (2016)
D.V. Else, C. Nayak, Phys. Rev. B 93, 201103 (2016)
C.W. von Keyserlingk, S.L. Sondhi, Phys. Rev. B 93, 245145 (2016)
C.W. von Keyserlingk, S.L. Sondhi, Phys. Rev. B 93, 245146 (2016)
A.C. Potter, T. Morimoto, A. Vishwanath, Phys. Rev. X 6, 041001 (2016)
S. Ray, A. Ghosh, S. Sinha, Phys. Rev. E 97, 010101 (2018)
M. Schreiber, S.S Hodgman, P. Bordia, H.P. Lüschen, M.H. Fischer, R. Vosk, E. Altman, U. Schneider, I. Bloch, Science 349, 842 (2015)
E. Maciá, ISRN Condens. Matter Phys. 2014, 1 (2014)
M.Ya. Azbel, Phys. Rev. Lett. 43, 1954 (1979)
C. Aulbach, A. Wobst, G-L. Ingold, P. Hänggi, I. Varga, New J. Phys. 6, 70 (2004)
M. Schreiber, S.S. Hodgman, P. Bordia, H.P. Lüschen, M.H. Fischer, R. Vosk, E. Altman, U. Schneider, I. Bloch, Science 349, 842 (2015)
D.C. Mattis, Rev. Mod. Phys. 58, 361 (1986)
K. Winkler, G. Thalhammer, F. Lang, R. Grimm, J.H. Denschlag, A.J. Daley, A. Kantian, H.P. Büchler, P. Zoller, Nature 441, 853 (2006)
J.A. Maruhn, P.G. Reinhard, E. Suraud, Simple Models of Many-Fermion Systems (Springer, Berlin, Heidelberg, 2010)
P.W. Anderson, Phys. Rev. 109, 1492 (1958)
K. Drese, M. Holthaus, Phys. Rev. Lett. 78, 2932 (1997)
A. Eckardt, M. Holthaus, H. Lignier, A. Zenesini, D. Ciampini, O, Morsch, E, Arimondo, Phys. Rev. A 79, 013611 (2009)
D. Romito, Periodic modulation of a quasicrystal, Master’s thesis, Università degli Studi di Trento, 2017
D.A. Abanin, W. De Roeck, F. Huveneers, Ann. Phys. 372, 1 (2016)
S. Gopalakrishnan, M. Knap, E. Demler, Phys. Rev. B 94, 094201 (2016)
J. Rehn, A. Lazarides, F. Pollmann, R. Moessner, Phys. Rev. B 94, 020201 (2016)
V. Mastropietro, Phys. Rev. B 93, 245154 (2016)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Romito, D., Lobo, C. & Recati, A. Localisation transition in the driven Aubry-André model. Eur. Phys. J. D 72, 135 (2018). https://doi.org/10.1140/epjd/e2018-90081-3
Received:
Revised:
Published:
DOI: https://doi.org/10.1140/epjd/e2018-90081-3