1 Introduction

The standard model of particle physics includes three flavors of neutrinos that interact through the weak force with other particles [53]. The neutrino flavors are identified by the corresponding charged lepton in charged current interactions. With the discovery [16, 36] of neutrino oscillations [46, 49], it became clear that neutrinos have mass. Currently the majority of observations is consistent with the standard picture of three mass eigenstates \((\nu _1,\nu _2, \nu _3)\) mixing with the flavor eigenstates \((\nu _e,\nu _\mu , \nu _\tau )\). The mixing is described by a \(3\times 3 \) unitary matrix (PNMS matrix), parametrized by three mixing angles \(\theta _{12}\), \(\theta _{13}\), \(\theta _{23}\) as well as a CP violating phase \(\delta \) and two Majorana phases if neutrinos are Majorana particles.

The neutrino experiments Double Chooz, Daya Bay, and RENO contributed to the field by establishing the third oscillation mode that is related to the mixing angle \(\theta _{13}\) [3, 17, 21]. These experiments observe the disappearance of \(\overline{\nu }_e\) from nuclear reactors by measuring the flux at different distances. The concept of multiple identical detectors has proven crucial in controlling and reducing systematic uncertainties. Today, the oscillation angle \(\theta _{13}\) is the most precisely measured oscillation parameter [53].

There have been speculations about the existence of additional neutrinos that are non-interacting with matter, see e.g. [1]. These thoughts are supported by experimental anomalies reported by the LSND [14] and MiniBooNE [15] neutrino-beam experiments as well as the so-called reactor [47] and gallium [2, 9, 39] anomalies, where the observed \(\overline{\nu }_e\) and \(\nu _e\) fluxes are roughly 5–10% less than the theoretical predictions. However, the uncertainty of those predictions remains an open question and our latest results [41] indicate a possible underestimation of the reactor flux prediction. Though this deficit is marginally compatible with the uncertainty of the flux prediction, it could be also interpreted as disappearance due to oscillation with additional neutrino states. Recently, the Neutrino-4 collaboration has reported [52] indications of a spectral distortion at short baseline to the reactor that would be consistent with the oscillation hypothesis. This result is subject of ongoing discussions [24, 31, 51]. Particularly it has been reviewed in [28] considering the validity of the Wilks- theorem, thus resulting in a reduced significance. Note that in this paper we report a very similar effect of reduced significance with respect to Wilks’ theorem in our measurement. From a phenomenological perspective it is important to emphasize that consistency of all today’s global data within a single simple solution remains an unsettled open debate, see e.g. [33].

The simplest extension of the standard oscillation picture is a \(3+1\) model [1]. Though this model cannot consistently explain all experimental anomalies, its few parameters make it well suited as a benchmark model in the following discussions. Here, one additional sterile, i.e. not weakly interacting, neutrino mixes with the three active neutrino states. This results in an additional mass state \(m_4\) and an extension of the mixing matrix to \(4\times 4\) with the additional parameters \(\theta _{14}\), \(\theta _{24}\), \(\theta _{34}\), and additional CP violating phases.

In this picture, a non-zero mixing of reactor \(\overline{\nu }_e\) with a sterile neutrino will result in a disappearance, superimposed to the standard oscillation related to \(\theta _{13}\). Assuming small mixing and baselines relevant for the Double Chooz experiment, only the parameters \(\theta _{14}\) and the difference of squared masses \(\varDelta m^2_{41} \equiv m_4^2 - m_1^2\) are relevant [43], and the survival probability of \(\overline{\nu }_e\) as a function of distance L and energy E can be approximated by

$$\begin{aligned}&P_{\overline{\nu }_e \rightarrow \overline{\nu }_e}\left( E, L\right) \approx 1 {-} \sin ^{2}\left( 2\theta _{13} \right) \sin ^{2}\left( {1.267}{MeV \over eV^2 m} \cdot \frac{\varDelta m^{2}_{ee} L}{E}\right) \nonumber \\&\quad {-} \sin ^{2}\left( 2\theta _{14} \right) \sin ^{2}\left( {1.267}{MeV \over eV^2 m} \cdot \frac{\varDelta m^{2}_{41} L}{E}\right) \end{aligned}$$
(1)

The first sine term corresponds to the disappearance related to the standard \(\theta _{13}\) mixing while the second sine term describes the additional disappearance due to the mixing with the sterile neutrino state. The term \( \varDelta m^{2}_{ee} \) is a shorthand for \( \cos ^2 \theta _{12} \, \varDelta m^2_{31} + \sin ^2 \theta _{12} \, \varDelta m^2_{32} \).

Fig. 1
figure 1

Survival probability of reactor \( \overline{\nu }_e \) as a function of the energy for the baselines of the ND (top) and FD (bottom) for different benchmark oscillation parameters \(\theta _{14}\) and \(\varDelta m^2_{41}\). The dotted line corresponds to the no-sterile case, where the survival probability is governed by the conventional \(\theta _{13} \) oscillation. The dashed and solid lines show two different examples of sterile mixing

Full size image

The effect is displayed in Fig. 1 for baselines of 400 m and 1050 m corresponding to the average distances of the nuclear reactors to the two Double Chooz detectors. The existence of sterile neutrinos with non-zero mixing leads to the additional disappearance superimposed on the conventional oscillation. The amplitude of this oscillation is given by the parameter \( \sin ^{2}\left( 2\theta _{14} \right) \). The oscillation frequency seen in the energy-dependence is proportional to the difference of squared masses. For mass differences of \(\varDelta m^2_{41} \gg {0.1}\,\mathrm{eV}^2 \), oscillations become fast. Given the experimental energy resolution, they become eventually indistinguishable from a global normalization change. Similarly, for small mass-square differences \(\varDelta m^2_{41} \approx \varDelta m^2_{ee} \simeq {2.5 \times 10^{-3}}\,\mathrm{eV}^2 \) the disappearance becomes indistinguishable from the conventional oscillation with \(\theta _{13}\). Note, that the above approximation is only used for illustrative purposes and for all numerical calculations in this analysis we use the full four-flavor propagation code nuCraft [55].

The position of the two Double Chooz detectors has been optimized for the measurement of \(\theta _{13}\) assuming \(\varDelta m^2 \approx {2.5 \times 10^{-3}}\,\mathrm{eV}{^2}\). For an energy range of detected reactor neutrinos between about from 1 to 8 MeV and the two baselines of 400 m and 1050 m, the probed L/E range for the disappearance of \(\overline{\nu }_e \) is approximately 50–1000 m/MeV. For larger mass differences, shorter baselines are desirable in order to observe the un-oscillated flux with a near detector. This is realized by short-baseline experiments, Bugey-3 [32] and more recently DANSS [18], NEOS [42], Neutrino-4 [52], PROSPECT [26], SoLID [8], and STEREO [19, 20], that target mass-square differences on the eV\(^2\) scale. The probed L/E range for these experiments is typically 1–20 m/MeV. Therefore the here presented search is complementary in probed L/E as well as lower probed mass-square differences below 0.1 eV\(^2\); see also [34].

2 Experimental setup

The Double Chooz experiment consists of two nearly identical gadolinium-doped liquid scintillator detectors [25] located close to the Chooz-B nuclear power plant, see Fig. 2. The power plant consists of two nuclear reactors of type N4, 165 m apart with a thermal power of about 4.25 GW each. The far (near) detector is located underground with an overburden of about 300 m (120 m) water equivalent at a distance of 1115 m and 998 m (469 m and 355 m) to the reactor cores.

Fig. 2
figure 2

The Double Chooz experiment. Left: arrangement of the two detectors far and near with respect to the nuclear reactors. Right: design of a Double Chooz detector. Figure modified from [41]

Full size image

Details of the detectors are described in [3, 4, 6, 41]. The detectors are constructed in an onion-like structure with a central detector made of four concentric cylindrical tanks. The innermost acrylic vessel contains 10.3 m\(^3\) gadolinium loaded liquid scintillator called the \(\nu \)-target. The \(\nu \)-target is surrounded by the \(\gamma \)-catcher, filled with 22.5 m\(^3\) liquid scintillator without gadolinium loading. Both central volumes serve as the neutrino target. A neutrino interacting in the target by inverse beta decay (\(\overline{\nu }_e+ p \rightarrow e^++n \)) [54] produces the characteristic signature of a delayed coincidence well known since the early days of neutrino experiments [29]. This is formed by a prompt signal from the positron and its annihilation and then the delayed signal from the capture of the thermalized neutron by either gadolinium or hydrogen. Though increasing the rate of accidental background events, the use of both types of captures in a combined data set greatly enlarges the sensitive volume and thus the statistics of detected neutrinos as well as reducing some of the systematic uncertainties. This technique, called total neutron capture, has been developed by the Double Chooz experiment for the most recent \(\theta _{13} \) analysis [41] and is applied also for this analysis.

The central target volumes are surrounded by a buffer volume filled with mineral oil, shielding the inner volume from radioactivity, partly from 390 10-inch PMTs that are installed on the inner wall of the stainless steel buffer tank and observe the target. Optically separated from these inner volumes is the inner veto. That is a 50 cm thick cylindrical volume filled with liquid scintillator and equipped with 78 8-inch PMTs. It actively shields the inner detector by tagging cosmic-ray induced muons, gammas, and neutrons from outside the detector. Shields of 15 cm thick demagnetized steel (1 m water) surround the inner veto of the far (near) detector, suppressing external gamma rays. A chimney in the top center allows deploying radioactive sources for calibration. Above the detector is the outer veto detector that adds to the shielding and allows for evaluating the efficiency of the inner veto detector.

Several key aspects of the Double Chooz experiment are important to this analysis. A main goal is avoiding dependencies on absolute predictions of the neutrino flux from the reactors as well as detection efficiencies. Therefore we perform a direct comparison of the event rates measured in the two identical detectors, in the following referred to as data-to-data approach. This results in the cancellation of most reactor flux related uncertainties as well as detection efficiencies and some of the background uncertainties in the measurement of \(\overline{\nu }_e\) disappearance. Furthermore, due to the presence of only two, relatively close reactor cores, the geometry constitutes well defined baselines from the reactors to the detectors which is important for testing faster oscillation modes than the \(\theta _{13} \) oscillation (see Fig. 1). The two detectors are situated close to the so-called iso-flux line, where the ratio of neutrino fluxes from the two reactors is the same for both detectors, i.e. the relative contribution from the two reactors is very similar in the two detectors, further reducing the reactor uncertainty. Another important aspect is that we include measurements when one of the reactors or even both reactors were switched off. These data allow for directly measuring the backgrounds and their spectral properties [5, 40]. In this analysis, the data from these off-reactor phases are used to construct templates of the energy distribution of backgrounds as well as the uncertainties of these templates for the fit to data. Additionally, the total rate is used to constrain the background rates.

Experimental backgrounds include uncorrelated backgrounds, where a single event appears in a random coincidence with another event, as well as correlated backgrounds that mimic both the prompt and the delayed event. The dominant sources of uncorrelated backgrounds are natural radioactivity and instrumental noise such as spontaneous light emission in the PMT bases of the far detector [7]. Correlated backgrounds are mostly caused by secondary products from cosmic ray air induced atmospheric muons that pass close or through the detectors. Muons reaching the detector are detected with high efficiency and cause an active veto of 1.25 ms duration. However, background events arise by (i) fast neutrons from interactions in the rock close to the detector entering the neutrino target, (ii) long lived isotopes, in particular \({^9Li}\) [40], that undergo \(\beta \)-decays followed by neutron emission, and (iii) low energy stopping muons that enter the detector through the chimney and decay by emission of a Michel electron. All these backgrounds are considerably reduced during the data selection and the remainder are measured with specific methods and in dedicated campaigns, e.g. during reactor-off phases.

The data of this analysis are identical to the selection described in [41] and are separated into three data sets. The first (FD-I) has been collected with the far detector prior to commissioning of the near detector and consists of 455.21 days of dead and down-time corrected livetime, collected between April 2011 and January 2013. The second set (FD-II) has been collected with the far detector during operation of both detectors and consists of 362.97 days of livetime collected between January 2015 and April 2016. The third set (ND) are the data collected during the same period with the near detector and corresponds to 257.96 days of livetime. Note that the effective livetime of the ND data is reduced with respect to the FD-II data, because the larger muon rate in the near detector causes a larger dead-time due to vetoing. While the previously described data has been collected during operation of at least one reactor, additionally 7.16 days of livetime with both reactors switched off during the FD-I phase are used to determine the total rate of background events.

3 Analysis method

The analysis is based on a profile likelihood ratio (see e.g. Cowan in [53]) that has already been exploited by Double Chooz for a measurement of \(\theta _{13} \) in [50] and has also been used internally to confirm the result in [41]. The test statistic is defined as the ratio of maximum likelihoods for tested model parameters \(\mathbf {\eta } =\{ \sin ^2 2 \theta _{14} , \varDelta m^2_{41} \}\) with respect to the globally largest likelihood value which is found for the parameters \(\hat{\mathbf {\eta }} =\{ \hat{\sin ^2 2 \theta _{14}} , \hat{\varDelta m^2_{41} }\}\). This defines the test statistic for the given data set \(\mathbf {x}\) and model parameters \(\mathbf {\eta }\)

$$\begin{aligned} \lambda (\mathbf {x},\mathbf {\eta }) = - 2 \cdot \ln \frac{\sup {\mathcal {L}} (\mathbf {x} | \mathbf {\eta } ,\mathbf {\xi }) }{\sup {\mathcal {L}} (\mathbf {x} | \hat{\mathbf {\eta }},\hat{\mathbf {\xi }} ) } = -2 \varDelta \ln ({\mathcal {L}}) \end{aligned}$$
(2)

In addition to the two model parameters \(\mathbf {\eta } \) that describe a sterile neutrino signal, the reactor fluxes, detector responses, systematic uncertainties and backgrounds are modeled by a total number of 298 additional and partly correlated parameters \(\mathbf {\xi } \) (see below for details). These parameters are treated as nuisance parameters in the fit. They are optimized separately for each respective signal hypothesis with \({\mathbf {\xi }} \) representing those nuisance parameters that maximize the local likelihood for the tested \(\mathbf {\eta } \).

For the test of a potential oscillation signal from sterile neutrinos, we compare the best-fit standard 3-flavor model (null hypothesis, \(\mathbf {\eta }_0\)), described by the two parameters \(\sin ^2 2 \theta _{14} =0 \) and \( \varDelta m^2_{41} =0\), to the globally best fit 3+1 sterile neutrino model (signal hypothesis) for the parameters \(\hat{\mathbf {\eta }} \) that maximize the likelihood of the data \(\mathbf {x}\). Note that specifically the null hypothesis \(\mathbf {\eta }_0\) is degenerate with respect to the two parameters \(\mathbf {\eta }\) because only one of them fixed to zero is sufficient to model a no-oscillation signal. Furthermore, \(\mathbf {\eta }_0\) is a special case, nested within the parameter space of the signal hypothesis resulting in \(\lambda (\mathbf {x} ,\mathbf {\eta }_0)\ge 0\).

The likelihood itself is implemented as a product of multiplicative terms with the Poissonian likelihoods \({\mathcal {P}}(n_i,\mu _i)\) of the observed number of events \(n_i\) in the energy bin i in all three data sets \(d \in \{ ND , FD-I , FD-II \}\) multiplied with Gaussian prior functions \({\mathcal {G}} \) on external nuisance parameters

$$\begin{aligned} \begin{aligned} {\mathcal {L}} (\mathbf {x} | \mathbf {\eta } ,\mathbf {\xi })&= \prod _{d\in \{ND,FD-I,FD-II\}} \ \prod _{i\in [E_{min}\dots E_{max} ]}\\&\quad {\mathcal {P}}(n_{d,i},\mu _{d,i}(\mathbf {\eta },\mathbf {\xi })) \\&\quad \cdot {\mathcal {P}}(n_{off},\mu _{off}(\mathbf {\xi }) ) \\&\quad \cdot \prod _{a\in \mathbf {\xi } } \left( {\mathcal {G}} (a, a_0, \sigma _a) \right) \\&\quad \cdot \prod _{\mathbf {b}\in \mathbf {\xi } } \left( {\mathcal {G}} ( (\mathbf {b}-\mathbf {b}_0)^T {\mathbf {V}}_b^{-1} (\mathbf {b}-\mathbf {b}_0) ) \right) \end{aligned}\nonumber \\ \end{aligned}$$
(3)

Here \(\mu _{d,i} (\mathbf {\eta },\mathbf {\xi })\) denotes the summed bin expectations of signal and backgrounds as a function of the model parameters. The second term is the Poisson probability of the observed event number during the reactor-off phases for the background expectation as a function of the nuisance parameters. The third term describes Gaussian priors for all single, uncorrelated nuisance parameters a with the expectation \(a_0\) and the uncertainty \(\sigma _a\). The fourth term describes Gaussian priors for all nuisance parameters \(\mathbf {b} \) that are correlated, described by the expectation \(\mathbf {b}_0 \) and the covariance matrix \({\mathbf {V}}_b \).

The data are binned for each of the three sets in 38 bins between 1 to 20MeV with custom bin sizes. The region up to 8 MeV which is dominated by measured reactor \(\overline{\nu }_e \) has 28 bins of 0.25 MeV size. Above 8 MeV, bins are background dominated but are included in the fit as they allow for constraining the background rates. Due to the lower statistics, larger bin sizes are used. These are 4 bins of 0.5 MeV size between 8 to 10 MeV, where rare isotopes (\({^9Li}\)) dominate and 4 bins of 2 MeV size between 12 to 20MeV, where fast neutrons dominate. In the intermediate region 10–12MeV, 2 bins of 1 MeV size are used.

Systematic uncertainties are modeled by the following nuisance parameters \( \mathbf {\xi }\) in the analysis (more details are given in [37]):

  • The normalizations of the reactor flux expectation for each energy bin are free fit parameters. This approach is independent of existing reactor flux predictions and the normalizations are only constrained by the data-to-data comparison of rate and shape of the data in each detector. This way, known discrepancies of reactor flux models [23, 41, 42, 44], being independent of the baseline, do not bias the fit, however, at the price of a slightly reduced sensitivity. The basis of the above approach is a large correlation in the observed reactor flux for the three data sets FD-I, FD-II, ND. Because of different running times, this assumption is only approximate, (99.75% for FD-II and ND, 93.20% for FD-I and FD2, 93.10% for FD-I and ND). Therefore, we model additional constraints on the normalization of each energy bin of the three data sets with a total of \(3\times 41\) reactor flux parameters between 1 to 11.25MeV. The number of parameters is determined by the greatest common divisor of the bin widths to create a uniform binning. These bins form the basis of an area conserving spline, which is energy corrected and later integrated over in the original binning. These parameters are correlated between the data sets with the above correlation factors and additionally we allow for uncorrelated shape deviations with a \(41\times 41\) covariance matrix for each data set, that is determined from the reactor flux prediction.

  • The conventional oscillation parameters \( \sin ^2 2\theta _{13} \) and \( \varDelta m^2_{ee} \) are free parameters. While \( \varDelta m^2_{ee} \) is seeded with the global best value from [48] and is constrained with a prior corresponding to its uncertainty, \( \sin ^2 2\theta _{13} \) is left unconstrained. The latter ensures that assumptions about the value, which has itself been largely determined in reactor neutrino experiments, cannot introduce a bias. By this, \( \sin ^2 2\theta _{13} \) can acquire a different best-fit value for \(\theta _{14} \ne 0\).

  • Backgrounds are modeled with free parameters for rate and shape. The shape of the contribution from rare isotopes (\({^9Li}\)) is assumed identical between the three data sets. It has been determined experimentally by a dedicated selection of events correlated in time and space with tagged muon events [6] and it is modeled with 38 shape parameters. The rate is assumed identical for FD-I and FD-II but is different for ND. Both total rates are not constrained by a prior but are determined by the data as free parameters during the fit. The rates and shapes of accidental backgrounds have been determined by time-scrambled experimental data for each data set and are individually modeled by 38 parameters for the shape and one parameter for the rate. These parameters are assumed uncorrelated for the three data sets, to account for changes in data taking over time and differences in the detectors but are constrained with a prior that reflects the uncertainty in the determination of the rates. The fast neutron and stopping muon backgrounds are modeled as \( R(E) = R_0 (a\cdot E + b\cdot \exp (-\lambda \cdot E) \). Here, \(R_0\) is the total rate and the three shape parameters \(\lambda \), a, and b are further constrained by the normalization. The shapes are assumed to be fully correlated between the data sets, while the rates are the same for for FD-I and FD-II but independent for ND. A special case is the small constant rate of \(\overline{\nu }_e \) from the reactor fuel that has been determined during FD-I reactor-off phases to \({0.58\pm 0.17}\,{d^{-1}}\). As these neutrinos undergo the same oscillation, this is modeled in the fit with the nominal oscillated shape expectation for \(\overline{\nu }_e \) and the rate is constrained by a prior corresponding to this reactor-off rate.

  • The uncertainties in the detector response are modelled identically to [41] by second order polynomials. They take into account the non-linearity of the visible energy response of the scintillator, the non-uniformity within the detector, and the charge non-linearity of the photomultiplier and electronics response. After analyzing the correlations of these effects where we assume the energy response of the scintillator to be fully correlated but the other effects to be uncorrelated between the data-sets, the 9 polynomial coefficients can be expressed by 7 independent parameters. In addition to the energy response, the total detection efficiency is subject to uncertainty, dominated by the uncertainty of the total target mass. This is modeled by a total of three constrained and partly correlated parameters.

The resulting expectations of reactor \(\overline{\nu }_e \) as well as the backgrounds for the default model are shown in Fig. 3 in comparison to the experimental data for all three data sets. In addition to the above parameters we have tested additional uncertainties but their effect was found to be negligible. In particular it was shown that the choice of mass ordering has no relevant impact on the analysis.

Fig. 3
figure 3

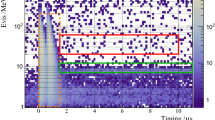
Visible energy distributions of the prompt events in the final data set. The ND (top) data is plotted with blue triangles and the FD-II (middle) and FD-I data are displayed as black squares. The different background model contributions are shown as stacked histograms where green indicates the long-lived isotopes (lithium) background, blue the accidental background and gray the fast neutron and stopping muon background. The red line indicates the total prediction from reactor models assuming no oscillations including the backgrounds

Full size image

The above fit has been extensively tested. These tests include a detailed validation of the \(\theta _{13} \) fit in the absence of a sterile signal that was found in good agreement to the published standard analyses of Double Chooz. Here, the relative impact of each systematic uncertainty has been evaluated by performing fits excluding the corresponding nuisance parameter (N − 1) or fits including exclusively this parameter on top of statistical uncertainties (stat + 1). All resulting uncertainties have been found in good agreement with the standard analysis [41].

For the validation of the detection of a sterile signal, studies of pseudo experiments with injected signal and blind data-challenges have been performed. Furthermore, the impact of each systematic parameter and other experimental effects, such as the spectral distortion at 5MeV have been tested. Here, it was verified that the fit results in an unbiased estimation of the parameters \(\sin ^2 2\theta _{14} \) and \(\varDelta m^2_{41}\).

4 Test statistic

The maximum likelihood is numerically obtained by minimizing the negative \(\log ({\mathcal {L}})\). However, finding the global minimum and \(\hat{\mathbf {\eta }}\) is numerically challenging because the fit does not converge for arbitrary combinations of initial signal and nuisance parameters to the global minimum. Therefore, the full phase space of signal parameters \(\mathbf {\eta }\) is scanned by performing a numerical fit of the parameters \(\mathbf {\xi }\) for each scan point. The result of such a scan is shown in Fig. 4 for an Asimov data set [30] based on Monte Carlo simulations of the null hypothesis of only standard oscillations. As the Asimov data set represents the mean expectation for this hypothesis, we thus find \( \lambda (\mathbf {x}) =0 \) for \(\sin ^2 (2\theta _{14} ) =0\) corresponding to the injected null hypothesis.

Fig. 4
figure 4

Test statistic \(\lambda (\mathbf {x},\mathbf {\eta }) \) for an Asimov data set \(\mathbf {x} \) of the null hypothesis for a scan of the signal parameter space. All values of \(\sin ^2 2\theta _{14} = 0\) represent the null hypothesis of no-sterile oscillations and correspondingly \(\lambda =0 \) for the Asimov data set. The color scale is clipped at \(\lambda =10 \). The lines represent the 68% and 95% sensitivity (see text) for constraining \(\sin ^2 2\theta _{14} \) as a function of \(\varDelta m^2_{41}\)

Full size image

As noted above, the null hypothesis is a special case nested within the more general signal hypothesis. The test statistic thus allows for a hypothesis test for a sterile signal i.e. non-zero \(\mathbf {\eta }\) with respect to the no-sterile case \(\mathbf {\eta }_0 =\mathbf {0}\) based on the likelihood ratio. If applied, Wilks’ theorem [56] would predict that the test statistic \(TS =\lambda (\mathbf {x}, \mathbf {\eta }_0 )\) follows a \(\chi ^2\) distribution with two degrees of freedom corresponding to the difference in degrees of freedom of the signal and null hypotheses. However, the preconditions for Wilks’ theorem are not fulfilled. First, the two parameters \(\sin ^2 2\theta _{14} \) and \(\varDelta m^2_{41}\) are degenerate in case of the null hypothesis. Any combination of these with one of the two parameters equal to zero is sufficient for fulfilling the null hypothesis even if the other parameter has a non-zero value. In many practical applications one can accommodate the problem by introducing an effective degree of freedom \(1 \le n_{eff} \le 2 \) and the value of \(n_{eff}\) can be estimated by pseudo experiments with the method introduced by Feldman and Cousins [35]. Secondly, the expectation value of partial derivatives with respect to the parameters \(||\langle \frac{\partial ^2 {\mathcal {L}} (\mathbf {x} | \mathbf {\eta })}{\partial \eta _i \ \partial \eta _j} \rangle || \) should form a positively definite matrix. Due to the oscillatory structure of the signal hypothesis, this is not the case here. A data fluctuation in any of the energy bins can be better described by some signal hypotheses that correspond to such an oscillatory pattern in the detectors. As a matter of fact, multiple, very different signal parameters can lead – within the experimental resolutions – to similar patterns. In an illustrative picture, for a statistical fluctuation of the experimental data bins in energy, multiple different combinations of signal parameters allow for a slightly improved description of the data with respect to the null hypothesis. As a result, multiple minima of the test statistic can be found within the signal parameter space. However, the existence of several minima implies that the above matrix of derivatives is zero in some points of the parameter space.

Fig. 5
figure 5

Example analysis of a pseudo data set representing the null hypothesis. The data set was generated with Poissonian fluctuations from a Monte Carlo data set. The blue line represent the 95% sensitivity (as defined in the text) for constraining \(\sin ^2 2\theta _{14} \) as a function of \(\varDelta m^2_{41}\)

Full size image

As verification of the above discussion, Fig. 5 shows an example analysis for a pseudo data set that was generated from a Monte Carlo simulation of the null hypothesis. The occurrence of multiple minima of the test statistic is well visible. As apparent features, these minima are horizontally elongated and thus correspond to a fixed value of \(\varDelta m^2_{41}\). Repeated pseudo experiments show similar features with, however, different number of minima and locations in each experiment. This supports the interpretation that for each possible statistical representation of the null hypothesis, multiple signal hypotheses can be found that describe the observed data slightly better than the average expectations from the null hypothesis. Each such solution requires a fixed oscillation length and is usually found close to the sensitivity-line beyond the region where a stronger signal would likely cause a more significant observation. More details on these observations can be found in [37]. We note that this has been independently discussed in [13] for short-baseline sterile neutrino searches and very recently in [28].

Fig. 6
figure 6

Expected distribution of test statistic values as obtained from 390 pseudo experiments of the null hypothesis. Also shown is the expectation for a \(\chi ^2\)-distribution with one and two degrees of freedom and various modified distribution functions (see text)

Full size image

As a consequence, the distribution of the test statistic values \(TS =\lambda (\mathbf {x}, \mathbf {\eta }_0 )\) cannot be approximated by a \(\chi ^2 \)-distribution but has to be derived from an ensemble study of pseudo experiments. Due to the huge computational effort for scanning the full parameter space, this has been possible only for limited statistics of a few hundred pseudo experiments. The resulting test statistic values TS when comparing the global minimum to the null hypothesis are shown in Fig. 6. It can be clearly seen that the test statistic strongly deviates from \(\chi ^2 \)-distributions of one and two degrees of freedom. Motivated by the fact, that the choice of the best of several random minima in the parameter space introduces a selection with trials (often called look-elsewhere effect), we introduce a trial factor in three versions of a modified approximation of the test statistic. For this, we calculate the probability distribution \(f_M(x) \) of the largest \(\chi ^2 \) value x from an ensemble M trials. This results to \(f_M(x) = M\cdot \chi ^2(x,n_{dof}) \cdot \left( \int _0^x \chi ^2(y,n_{dof})\, dy \right) ^{M-1} \) where \(\chi ^2(x,n_{dof}) \) is the p.d.f. of a single trial. Three versions of this approximation with M as a free parameter are fitted to the pseudo experiments, using \(\chi ^2 \) distributions of one, two, and a fitted degree of freedom \(n_{dof} \). All three versions describe the observed test statistic reasonably well. Particularly the case of \(n_{dof} = 2\) results in a fitted \(M\simeq 6 \) which agrees well with the observations in pseudo experiments.

Fig. 7
figure 7

Test statistic for fixed values of \(\varDelta m^2_{41}\). Shown are the results from 1999 pseudo experiments when fitting \(\sin ^2 2\theta _{14} \) for 100 discrete values of \(\varDelta m^2_{41}\) for the injected null hypothesis. For comparison, the expectation from a \(\chi ^2\) distribution of one degree of freedom is shown. Additionally the test statistic for 1997 pseudo experiments of an injected signal is shown. Here the median of the fit \(\sin ^2 2\theta _{14}^{med} \) has been determined for each of the 100 tested \(\varDelta m^2_{41}\) values. The test statistic is then evaluated with \(\sin ^2 2\theta _{14}^{med} \) instead of \(\sin ^2 2\theta _{14} = 0 \) as the null hypothesis. All distributions are found to be consistent

Full size image

The situation becomes simpler, when taking into account that multiple values of \(\varDelta m^2_{41}\) can cause a minimum in the test statistic. In a modified hypothesis, we can define the sensitivity as the ability to test values of \(\sin ^2 2\theta _{14} \) as a function of \(\varDelta m^2_{41}\). When analyzing the pseudo experiments in a raster-scan for distinct fixed values of \(\varDelta m^2_{41}\) and varying only \(\sin ^2 2\theta _{14} \) [35], a distribution that is well compatible with the expectation from a \(\chi ^2\) distribution with one degree of freedom is found as shown in Fig. 7. Also for an injected signal, the test statistic with respect to the median expectation of the null hypothesis is consistent and also described by the same \(\chi ^2\) distribution. This is a good confirmation of our assumption that the observed trials are only related to different degenerated oscillation lengths. This test shows that in this case the test statistic can be well described with a \(\chi ^2\)-distribution of one degree of freedom in agreement with Wilks’ theorem.

5 Sensitivity

We define the sensitivity, in the following denoted as Asimov-Wilks’ (AW) sensitivity, by the boundary value \(\sin ^2 2\theta _{14} \) as a function of \(\varDelta m^2_{41}\) where the test statistic of the Asimov data set has a value \(\langle \lambda (\mathbf {x}) \rangle \ge 3.84 \) (or \(\langle \lambda (\mathbf {x} ) \rangle \ge 1 \)). This corresponds to the boundary of the median signal expectation where in case of absence of a signal 95% (or 68%) of experiments obtain a smaller value of \(\sin ^2 2\theta _{14} \). Note, that because an Asimov data set of the null hypothesis contains no fluctuations, the use of Wilks’ theorem is valid and not in contradiction with the above discussion. Furthermore, the best found likelihood always corresponds to the injected null hypothesis. As the null hypothesis is degenerate in \(\varDelta m^2_{41}\), this choice of sensitivity corresponds effectively to a one-dimensional sensitivity on the maximum allowed value of \(\sin ^2 2\theta _{14} \) as a function of \(\varDelta m^2_{41}\), also known under the term raster-scan [45]. This choice is consistent with the final choice of experimental limit that will be discussed below. Also, choosing a \(\chi ^2\) distribution of one degree of freedom for the test statistic value of 95% coverage is a result of this degeneracy.

This choice of sensitivity marks the region, where larger values of \(\sin ^2 2\theta _{14} \) are expected to lead to indications of a signal on the level of two (or one) standard deviations but is also closely related to the ability of constraining \(\sin ^2 2\theta _{14} \) in the absence of a signal. These sensitivities are shown as lines in Figs. 4 and 5. The statistical coverage of the AW-sensitivity as well as the unbiased estimation of the model parameters \(\sin ^2 2\theta _{14} \) and \(\varDelta m^2_{41}\) have been verified with ensembles of pseudo data in [37].

For small values of \(\varDelta m^2_{41} \lesssim {5 \times 10^{-3}}\,\mathrm{eV}{^2}\), the sensitivity becomes weaker as the disappearance becomes ambiguous with conventional oscillations whose energy dependence is given by \(\varDelta m^2_{ee} \). The free nuisance parameter \(\sin ^2 2\theta _{13}\) becomes degenerate with \( \sin ^2 2\theta _{14} \) and the sensitivity decreases. Also towards large values of \(\varDelta m^2_{41} \gtrsim {0.3}\,\mathrm{eV}{^2} \) the sensitivity decreases, because oscillations become fast, and the disappearance turns into an overall deficit for both detectors. For the data-data fit approach as implemented here, an oscillation signal would thus become increasingly indistinguishable from an overall change of the reactor flux normalization. We have tested that by additionally constraining the fit with a flux prediction. The sensitivity above \(\varDelta m^2_{41} \gtrsim {0.3}\,\mathrm{eV}{^2} \) would strongly improve but also become strongly model dependent. An interesting observation is the dip in sensitivity at \( \varDelta m^2_{41} \simeq {5 \times 10^{-2}}\,\mathrm{eV}{^2} \). The effect is related to the interference of maximum and minimum disappearance for neutrinos from the two reactor cores to the two detectors, whose baselines differ by about \({\sim 100}\,{m}\). A strong disappearance for signals of one of the reactor is counteracted by no disappearance for the other reactor. We have tested that the effect disappears when simulating the baseline of only one reactor core.

Fig. 8
figure 8

Sensitivity (95% C.L.) of the analysis as obtained from Asimov data sets with and without a spectral distortion at 5 MeV

Full size image

The effect of the aforementioned spectral distortions of reactor flux models has been studied with two Asimov data sets. One of them included a bump-like distortion at 5 MeV using a double-Gaussian approximation of the measurement in [23]. The resulting sensitivity is only marginally impacted as shown in Fig. 8.

6 Experimental result

The result of the scan of the test statistic \(\lambda (\mathbf {x} ) \) for the experimental data is shown in Fig. 9.

Fig. 9
figure 9

Likelihood scan of the experimental data

Full size image

The global best fit minimum is found for the values \( \hat{\sin ^2 2\theta _{14}} = 0.043 \) and \( \hat{\varDelta m^2_{41}} = {0.028}\,\mathrm{eV}{^2}\). The nuisance parameters converged to values within their reasonable range. In particular the best fit value \(\sin ^2 2\theta _{13} = {0.108^{+0.016}_{-0.017}}\) of the null hypothesis is found in agreement with the nominal value 0.105+-0.014 that has been obtained from the same data set [41]. The difference to that result is expected from the differences of the fit method and has been verified in a detailed comparison of the fit methods. Also the value \( \sin ^2 2\theta _{13} = 0.1077 \) obtained for the global best fit \( {\hat{\eta }} \) is very close to the null hypothesis and thus does not indicate a pull on the best fit.

The value of the test statistic of the best fit with respect to the null hypothesis of no sterile mixing is \(\lambda (\mathbf {x}_{exp} ) = 6.15 \). From 388 performed pseudo experiments of the null hypothesis in Fig. 6, a total of 96 have a larger or equal value of \(\lambda \). The corresponding p value is \({24.7 \pm 2.2 }\)%. This p value does not depend on details of the modeling of the test statistic. When using the three approximations of the test statistic distributions in Fig. 6, very similar p values between 22 to 26% are obtained. Therefore, the experimental result is fully consistent with the null hypothesis of no mixing with sterile neutrinos and no evidence for a signal can be reported.

The location of the best-fit point is not within the region of good sensitivity but close to the estimated sensitivity line, see Figs. 4 and 8. This is, as discussed above, an expected feature of statistical background fluctuations that are being picked up by a signal model.

Fig. 10
figure 10

Experimental residuals for the three consistently fitted data sets FD-I, FD-II, and ND. The data are normalized to the nominal reactor expectation [38] adapted to the Double Chooz reactors including conventional oscillations with parameters taken from an independent measurement [12]. The experimental data are plotted as red dots. The global best fit is shown as a solid line while for comparison the best-fit null hypothesis is shown as a dashed line. As the fit optimizes systematic uncertainties to the data, only statistical error bars are displayed

Full size image

Figure 10 shows the fit residuals normalized to the number of events expected for the nominal reactor-model including conventional oscillations. Also shown are the best fit of the null (non-sterile) and best-fit sterile hypothesis. All three data sets are consistently described by both models with a generally good agreement, including the observed bump at 5 MeV and other spectral features, as expected from the implementation of the fit. No particular difference is observed between the three data sets that would hint to a mismodeled detector responses. Note that due to the use of a free but global normalization for each energy bin, the fit does not depend on the assumed shape and normalization of the initial reactor flux model but only on the consistency of the measured experimental data in the three data sets. The sterile model achieves a marginally better description. The difference can be quantified by Pearson’s \(\chi ^2 \)-test [53]. The summed \(\chi ^2\) values of the three data distributions of Fig. 10 are 78.17 for the best-fit no-sterile model and 71.91 for the best-fit sterile model, respectively. With a rough estimation of the number of degrees of freedom of 76, i.e. the number of data points corrected for the free overall normalizations of each energy bin, this indicates an acceptable goodness of fit for both models. The difference \(\varDelta \chi ^2 = 6.25\) shows no systematic trend and is largely driven by a few fluctuating data points, i.e. the two energies 4.1 MeV and 5.6 MeV dominate the difference with a summed contribution of \(\varDelta \chi ^2 = 5.5\). As discussed above, this is an expected behavior also for the no-sterile case where for each statistical fluctuation of data a matching sterile hypothesis can be constructed. No general trend in the data supporting a sterile signal is observed, which is consistent with the observation of an insignificant p value as reported above.

7 Discussion

The experimental data has been tested over the full range of the two-dimensional signal parameter space. The globally found minimum does not constitute a significant observation of a signal but is well compatible with the null hypothesis of no mixing with sterile neutrinos.

In response to the limited computing resources that do not permit the evaluation of the test statistic with pseudo experiments at every point in the two-dimensional parameter space with sufficiently accurate coverage, we have decided for a more robust limit-setting strategy which is also known under the term raster-scan [45]. Here, we calculate one-dimensional exclusion limits on the maximum allowed value of \(\sin ^2 2\theta _{14} \) as a function of \(\varDelta m^2_{41}\). These limits are calculated with a frequentist approach based on Wilks’ theorem comparing the local test statistic with respect to the best fit at the probed \(\varDelta m^2_{41}\) and using the \(\chi ^2\) probability with one degree of freedom. The statistical coverage of the approach has been verified with pseudo experiments of injected signal as shown above.

Alternatively a two-dimensional approach could be pursued, where the test statistic is compared to the globally found maximum likelihood. Such a strategy has been followed e.g. for the analysis in Daya Bay [23]. Here the exclusion would correspond to the probability of the combination of \(\sin ^2 2\theta _{14} \) and \(\varDelta m^2_{41}\). However, pseudo experiments with an injected signal have revealed that our test statistic strongly depends on the injected value of \(\sin ^2 2\theta _{14} \). For small values of \(\sin ^2 2\theta _{14} \) it is close to the test statistic that we have observed for the null hypothesis (see Fig. 4) while it gradually crosses over into a \(\chi ^2\)-distribution of two degrees of freedom for larger values. Because the determination of limits with correct statistical coverage would require the simulation of a very large number of pseudo experiments throughout the entire parameter space, we have chosen the raster-scan approach. Within the available computing resources this resulted in limits of more accurate coverage. We note that this strategy applies only to the setting of limits but not to the p value of the analysis that has been obtained in a full two-dimensional approach.

Fig. 11
figure 11

Upper limit (dotted blue line) at 95% C.L. for \(\sin ^2 2\theta _{14} \) as a function of \(\varDelta m^2_{41}\). The black dot indicates the position of the global best fit. The green solid line corresponds to the AW-sensitivity

Full size image

The resulting exclusion limits are shown in Fig. 11. The obtained limits are generally close to the AW-sensitivity. For masses \(\varDelta m^2_{41}\), where the best fit results in the null hypothesis \(\sin ^2 2\theta _{14} =0 \), the upper limit coincides with the median expected sensitivity. Due to statistical fluctuations in the data one expects variations around this median sensitivity, depending whether excesses or deficits in the prediction match these fluctuations better. As the allowed parameter space is bounded to positive values of \(\sin ^2 2\theta _{14} \), we expect roughly for 50% of probed \(\varDelta m^2_{41}\) values fits with a non-zero value of \(\sin ^2 2\theta _{14} \) resulting in less constraining limits than the average sensitivity and similarly a roughly equal number of more constraining limits.

Fig. 12
figure 12

Comparison of the upper exclusion limits provided by this analysis (Double Chooz) with results from other measurements: Daya Bay [11], RENO [27], Bugey-3 [32] Neos [42], and cosmological limits [10] based on the combination of observations of the cosmic microwave background, gravitational lensing and baryon-acoustic oscillations. Additionally displayed is the expected average sensitivity of Double Chooz with the full data statistics from the multi-detector phase. Note, that the figure combines 1-d and 2-d limits as well as limits of different confidence level

Full size image

As discussed above, both experiments Daya Bay and RENO probe a similar range of L/E values and have published exclusion limits for a similar range of \(\varDelta m^2_{41}\) for sterile neutrino mixing in the 3 + 1 model [11, 22, 27]. A comparison of these results is shown in Fig. 12. We note, that a detailed quantitative comparison is difficult, because, unlike Double Chooz and as discussed above, the two other experiments provide two-dimensional limits. In order to quantify the difference, we have evaluated the consistency of the two-dimensional and one-dimensional raster-scan approach with seven pseudo experiments of the null-hypothesis. It is found that the median line of the 2-d TS value of 8.7, corresponding to a 10% p value in Fig. 6 matches within about 10–20% with the 90% AW-sensitivity. Furthermore, marginalizing the TS values of the 2-d contours of these pseudo experiments for every \(\varDelta m_{41}^2 \) value and averaging the pseudo experiments matches well with the 1-d AW-sensitivity without noticeable bias. Another important difference with respect to the aforementioned experiments is that analysis assumptions differ. In particular, the Daya Bay result includes a reactor flux model and constraints on \(\theta _{13}\). We have tested that such assumptions would also increase the sensitivity of this analysis. The statistics of \(\overline{\nu }_e \) candidates used in Daya Bay and RENO is roughly four times the statistics used here. In addition, the figure shows limits obtained by the Bugey-3 collaboration and limits from combining cosmological observations. The Double Chooz result based on the here used data is less constraining than Daya Bay but is competitive to the other presented results.

The result has been obtained under the assumption of a 3 + 1 model. An extension to a 3 + 2 model would require the extension of the \(3\times 3\) PMNS Matrix to \(5\) dimensions with 7 additional mixing angles plus additional CP phases and the oscillations would also involve additional mass differences. In the simplest approximation, Eq. (1) would include an additional term \(-\sin ^2 2\theta _{15} \sin ^2\varDelta m^2_{51} L/(4E) \). This leads to additional oscillations, which potentially interfere with the 4-1 oscillation if \(\varDelta m^2_{41} \approx \varDelta m^2_{51} \). As a result of test studies [37], we find that the here presented limits of the mixing angle as a function of \(\varDelta m^2 \) are largely valid also for 3+2 models with largely different mass difference and in particular if \(\varDelta m^2_{51} \gtrsim {0.3}{eV^2} \). In case both mass-square differences fall into the sensitive region of this analysis, the oscillation of the respective larger \(\varDelta m^2 \) is largely washed out and results in a global normalization offset, to which the data-to-data fit of this analysis is insensitive. In summary, though different in statistical coverage, the test for a 3 + 1 model is also sensitive for a signal of a more complicated model.

The relative impact of systematic uncertainties has been tested in terms of sensitivity for the null hypothesis and for relatively strong signals of \(\sin ^2 2\theta _{14} =0.1\) and varying values of \(\varDelta m^2_{41}\). It is found that the relative impact of systematic uncertainties on the total error increases towards smaller values \(\varDelta m^2_{41}\). E.g. for determining the value \(\sin ^2 2\theta _{14} =0.1\) the relative error changes from \({\sigma _{stat} \over \sigma _{tot} } = {99}{\%}\) for \(\varDelta m^2_{41} = {0.1}{eV^2}\) to \({\sigma _{stat} \over \sigma _{tot} } = {55}{\%}\) for \(\varDelta m^2_{41} = {7.3 \times 10^{-3}}{eV^2}\). Among the different systematic parameters, the uncertainty of the energy scale and the unconstrained parameter \(\theta _{13}\) show the largest impact on the total uncertainty. As the current analysis is limited by statistics, it will benefit from the full data set of Double Chooz. Figure 12 shows the expected median sensitivity for the full duration of multiple detector operation, corresponding to an increase in statistics by roughly a factor 2.4. In addition, we expect improvements by the off-reactor data set, that is enlarged from 7 to 32 days, resulting in reduced uncertainties in background modeling and furthermore the planned improved measurement of the proton number of the neutrino target.

8 Summary

We have presented an initial search for oscillations of electron anti-neutrinos with additional sterile neutrino flavors with the Double Chooz experiment. The search uses data from five years of operation of Double Chooz, including two years in the two-detector configuration. The analysis method is based on a profile likelihood, searching for the disappearance due to oscillations in a data-to-data comparison of the two respective detectors. The analysis is optimized for a 3+1 model and is sensitive in the mass range \({5 \times 10^{-2}}\,\mathrm{eV}{^2} \lesssim \varDelta m^2_{41} \lesssim {3 \times 10^{-1}}\,\mathrm{eV}{^2} \). No significant disappearance signal additionally to the conventional oscillations related to \(\theta _{13} \) is observed in a full 2-d scan of the model parameters. Correspondingly exclusion bounds on the sterile mixing parameter are determined in form of a raster-scan of \(\theta _{14} \) as a function of \( \varDelta m^2_{41} \). The result is competitive to similar searches in this mass range. An update to the full data set from Double Chooz is planned.