Conformal GUT inflation, proton lifetime and non-thermal leptogenesis

Abstract

In this paper, we generalize Coleman–Weinberg (CW) inflation in grand unified theories (GUTs) such as $\text {SU}(5)$ and $\text {SO}(10)$ by means of considering two complex singlet fields with conformal invariance. In this framework, inflation emerges from a spontaneously broken conformal symmetry. The GUT symmetry implies a potential with a CW form, as a consequence of radiative corrections. The conformal symmetry flattens the above VEV branch of the CW potential to a Starobinsky plateau. As a result, we obtain $n_{s}\sim 1-\frac{2}{N}$ and $r\sim \frac{12}{N^2}$ for $N\sim$ 50–60 e-foldings. Furthermore, this framework allow us to estimate the proton lifetime as $\tau _{p}\lesssim 10^{40}$ years, whose decay is mediated by the superheavy gauge bosons. Moreover, we implement a type I seesaw mechanism by weakly coupling the complex singlet, which carries two units of lepton number, to the three generations of singlet right handed neutrinos (RHNs). The spontaneous symmetry breaking of global lepton number amounts to the generation of neutrino masses. We also consider non-thermal leptogenesis in which the inflaton dominantly decays into heavy RHNs that sources the observed baryon asymmetry. We constrain the couplings of the inflaton field to the RHNs, which gives the reheating temperature as $10^{6}\text { GeV}\lesssim T_{R}<10^{9}$ GeV.

1 Introduction

Primordial inflation is a successful paradigm for the description of the early Universe and it is strongly supported by the current observational data [1,2,3,4,5,6]. Primordial perturbations, when the scales exiting the horizon $\left( k\sim aH\right)$, are eventually responsible for the structure formation in the Universe. From Planck 2015 [6, 7], the key observables of inflation, namely, the scalar tilt and the ratio of tensor to scalar power spectra, are constrained as $n_{s}=0.968\pm 0.006$, $r<0.09$ at $95\%$ confidence level. The CMB power spectra is observed to be nearly adiabatic, scale invariant and Gaussian [6, 8]. Although the physical nature of the inflaton is still uncertain [9, 10], the models based on f(R) or a canonical scalar field with a flat potential are favoured with respect to the data. Since the inflationary scale is in general expected to be $\sim 10^{16}\,\text {GeV}$, it is natural consider the inflaton to be a scalar field associated with grand unified theory (GUT) groups, such as $\text {SU}(5)$ and $\text {SO}(10)$. The Shafi-Vilenkin (SV) model [11] is one of the first realistic model of inflation which was based on $\text {SU}(5)$ GUT [12]. In this framework, inflation is a result of the spontaneous breaking of $\text {SU}(5)\rightarrow \text {SU}(3)_{c}\times \text {SU}(2)_{L}\times \text {U}(1)_{Y}$ by a GUT field (24-plet adjoint Higgs) and an inflaton, which is a SU(5) singlet that rolls down to a vacuum expectation value (VEV). The success of the SV model is that it can lead to a successful baryogenesis after inflation and predicts a proton life time above the current lower bound [13, 14]. In this model, the scalar field potential is of a Coleman–Weinberg (CW) form, according to which primordial gravitational waves are constrained by $0.02\le r\le 0.1$ [15]. Although the SV model is well within the current bounds of Planck 2015, several extensions of this model were studied to get smaller values of r. In [16,17,18,19,20], CW inflation was studied in the context of induced gravity, non-minimal coupling and brane-world scenario, where the tensor to scalar ratio was obtained to be $r\sim \mathcal {O}\left( 10^{-2}\right) -\mathcal {O}\left( 10^{-3}\right)$. We note that all these modifications necessarily introduce an additional parameter whose value determines the shape of the inflaton potential in the Einstein frame.¹

Moreover, extensions of the SV model within particle physics offer rich physics beyond the Standard Model (SM). Therefore, the SV model is embedded in a higher gauge group such as $\text {SO}\left( 10\right)$, which can be broken to the SM via an intermediate group $\text {G}_{422}=\text {SU}(4)_{c}\times \text {SU}\left( 2\right) _{L}\times \text {SU}\left( 2\right) _{R}$ [23, 24]. Obtaining successful inflation in $\text {SO}\left( 10\right)$ is more realistic with additional benefits to explain physics beyond SM, such as neutrino physics, matter anti-matter asymmetry through non-thermal leptogenesis, monopoles and dark matter (DM) [14]. For example, Ref. [25] considered a complex singlet scalar being coupled to right handed neutrinos (RHNs), followed by implementing type I seesaw mechanism. This approach unified inflation with Majorana DM together with the scheme of generating neutrino masses. In [26] an additional $\text {U}(1)_{B-L}$ symmetry was considered in the SM i.e., $\text {SU}(3)_{c}\times \text {SU}(2)_{L}\times \text {U}(1)_{Y}\times \text {U}\left( 1\right) _{B-L}$, where $B-L$ symmetry can be spontaneously broken when the scalar field takes the VEV. In this setup, we can explain the baryon asymmetry of the Universe through non-thermal leptogenesis [24, 27,28,29]. Recently, CW inflation was studied in an extension with $\text {SO}(10)$ and $\text {E}_{6}$, pointing out the possibility of observing primordial monopoles [30].

Apart from models based on GUT theories, the Starobinsky model based on the $R^{2}$ gravity modification and the Higgs inflation [1, 31, 32] occupy a privileged position, with practically equal predictions in the $\left( n_{s},\,r\right)$ plane

$$\begin{aligned} n_{s}=1-\frac{2}{N},\quad r=\frac{12}{N^{2}}\,, \end{aligned}$$

(1)

where N is the number of e-foldings before the end of inflation. There has been a growing interest on embedding these models in string theory and supergravity (SUGRA) aiming for a UV completion [33, 34]. Recently, a UV completion of the Starobinsky model was proposed in the context of non-local gravity inspired from string field theory [35, 36]. Starobinsky like models were also developed in $\mathcal {N}=1$ SUGRA, namely, no scale [37] and $\alpha$-attractor models [38] where an additional physical parameter leads to any value of $r<0.1$. In [39] $\alpha -$attractor models were studied in the non-slow-roll context where a new class of potentials were shown to give the same predictions. On the other hand, Higgs inflation is particularly interesting due to the fact that Higgs was the only scalar so far found at LHC. But for it to be an inflaton candidate compatible with CMB data, we require a very large non-minimal coupling $\left( \xi \gg 1\right)$ to Ricci scalar. It was known that a scalar field with large non-minimal coupling gives rise to a $R^{2}$ term considering 1-loop quantum corrections. Consequently, renormalization group (RG) analysis shows that Higgs inflation is less preferable compared to Starobinsky model [40, 41]. This result not only applies to Higgs inflation but also to any arbitrary scalar with very large non-minimal coupling. Furthermore, in both $R^{2}$ and Higgs inflation the inflaton field rolls down to zero after inflation.² Differently, in GUT theories the inflaton field acquires a VEV due to its interaction with GUT fields.

The main goal of this paper is to generalize the SV model in order to achieve $r\sim \mathcal {O}\left( 10^{-3}\right)$ without introducing any additional parameters that affect the flatness of the inflaton potential (in Einstein frame), coasting towards a Starobinsky plateau.³ In our construction, we introduce conformal symmetry (or local scale invariance) in a GUT model. It was shown by Wetterich [42] that scale symmetries play a crucial role in the construction of realistic cosmological models based on particle physics. Moreover, scale symmetries successfully explain the hierarchy of different scales such as the Planck and the Higgs mass [43,44,45,46]. Therefore, it is natural to consider scale invariance in constructing an inflationary scenario, through which we can obtain a dynamical generation of the Planck mass, inflationary scale and particle physics scales beyond SM. In this regard, we consider two complex singlet fields $\left( \bar{X},\,\Phi \right)$ of $\text {SU}(5)$ or $\text {SO}(10)$ and couple them to the Ricci scalar and adjoint Higgs field $\left( \Sigma \right)$, such that the total action would be conformally invariant. We obtain inflation as a result of spontaneous breaking the conformal and GUT symmetries. The former occurs due to gauge fixing of one singlet field to a constant for all spacetime and the latter occurs due to $\Sigma$ field taking its GUT VEV. Here the inflaton is identified with the real part of the second singlet ($\phi =\sqrt{2}\mathfrak {Re}\left[ \Phi \right]$), whereas the imaginary part is the corresponding Nambu–Goldstone boson is assumed to pick up a mass due to the presence of small explicit soft lepton number violation terms in the scalar potential [25]. We also assume $\Phi$ carries two units of lepton number and it is coupled to the RHNs. Near the end of inflation, the inflaton is supposed to reach its VEV and also the global lepton number is violated. Thereafter, we study the dominant decay of inflaton into heavy RHNs producing non-thermal leptogenesis. We compute the corresponding reheating temperatures and also discuss the issue of producing the observed baryon asymmetry. Our study completes with an observationally viable inflationary scenario, predicting proton life time, neutrino masses and producing non-thermal leptogenesis from heavy RHNs.

The paper is briefly organized as follows. In Sect. 2, we describe toy models with conformal and scale invariance. We identify the interesting aspects of spontaneous symmetry breaking of these symmetries leading to viable inflationary scenarios. In Sect. 3, we briefly present the SV model and the computation of the proton life time. In Sect. 4 we propose our generalization of the SV model by introducing an additional conformal symmetry. We report the inflationary predictions of the generalized model together with estimates of proton life time. In Sect. 5 we further explore the nature of inflaton couplings to the SM Higgs and singlet RHNs through type I seesaw mechanism. In the view of the dominant decay of the inflaton into heavy RHNs, we constrain the Yukawa couplings of the inflaton field compatible with the generation of light left handed neutrino masses. In Sect. 6 we implement non-thermal leptogenesis and compute the reheating temperatures corresponding to the dominant decay of inflaton to heavy RHNs. We additionally comment on the necessary requirements for the production of observed baryon asymmetry through CP violation decays of RHNs. In Sect. 7 we summarize our results pointing to future steps. We provide an Appendix A summarizing the effects of geometric destabilization from fields space of inflaton and the presence of heavy fields in our model. In this paper we follow the units $\hbar =1,\,c=1,\,$ $m_\mathrm{P}^{2}=\frac{1}{8\pi G}$.

2 Conformal vs scale invariance

Models with global and local scale invariance [Weyl invariance (or) conformal invariance] are often very useful to address the issue of hierarchies in both particle physics and cosmology [43,44,45, 47,48,49]. Models with these symmetries contains no input mass parameters. The spontaneous breaking of those symmetries induced by the VEV’s of the scalar fields present in the theory, generates a hierarchy of mass scales e.g., Planck mass, GUT scale and neutrino masses.⁴ Moreover, it is a generic feature that scale or conformal symmetry breaking induce a flat direction in the scalar field potential [42], which makes these models even more interesting in the context of inflation. Another motivation to consider scale invariance for inflationary model building comes from CMB power spectra which is found to be nearly scale invariant [6].

In this section, we present firstly a toy model (with two fields) that is (global) scale invariant and present the generic form of (scale invariant) potentials and their properties. We review the presence of a massless Goldstone boson that appears as a result of spontaneous breaking of global scale invariance. In the following, we discuss the two field conformally invariant model, in which case the presence of a massless Goldstone boson can be removed by appropriate gauge fixing. The resultant spontaneous breaking of conformal symmetry (SBCS) turns to be very useful to obtain a Starobinsky like inflation.^{5 6} We will later explore the role of SBCS in a more realistic inflationary setting based on GUTs.

2.1 Scale invariance

Here we discuss a toy model with two scalar fields (in view of Refs. [42, 53, 62, 63]) and point out interesting features that we later utilize in our construction.

A generic two field global scale invariant action can be written as

$$\begin{aligned} S_{global}= & {} \int d^{4}x\,\sqrt{-g}\left[ \frac{\alpha }{12}\phi ^{2}R+\frac{\beta }{12} \chi ^{2}R-\frac{1}{2}\partial ^{\mu }\phi \partial _{\mu }\phi \right. \nonumber \\&\left. -\frac{1}{2}\partial ^{\mu }\chi \partial _{\mu }\chi -\phi ^{4}f \left( \rho \right) \right] , \end{aligned}$$

(2)

where $\alpha ,\,\beta$ are constants and $\rho =\frac{\phi }{\chi }$, the generic function $f\left( \frac{\phi }{\chi }\right)$ here can be treated as quartic self coupling of the field $\phi$ [42, 63]. The action (2) is scale invariant, i.e., invariant under global scale transformations $g_{\mu \nu }\rightarrow e^{-2\lambda }g_{\mu \nu }\,,\,\phi \rightarrow e^{\lambda }\phi \,,\,\chi \rightarrow e^{\lambda }\chi$ for any constant $\lambda$ (dilatation symmetry).

Since the potential $V\left( \phi ,\,\chi \right) =\phi ^{4}f\left( \rho \right)$ is homogeneous, it must satisfy the following constraint [53, 63]

$$\begin{aligned} \phi \frac{\partial V}{\partial \phi }+\chi \frac{\partial V}{\partial \chi }=4V. \end{aligned}$$

(3)

The extremum conditions for V, i.e., $\partial _{\phi }V=\partial _{\chi }V=0$ can also be written as $f\left( \rho \right) =f^{\prime }\left( \rho \right) =0$. One of the conditions fix the ratio of the VEV’s of the fields, while the other gives a relation between couplings (if $\langle \phi \rangle \ne 0$ and $\langle \chi \rangle \ne 0$). The interesting property here is that if $\langle \phi \rangle \propto \langle \chi \rangle$ there exists a flat direction for the field $\phi$ (see [42] for detailed analysis). This will be more useful in the context of local scale invariant model.

Let us consider a scale invariant potential of the form

$$\begin{aligned} V_{1}=\frac{\lambda _{\phi }}{4}\phi ^{4}+\frac{\lambda _{m}}{2}\phi ^{2} \chi ^{2}+\frac{\lambda _{\chi }}{4}\chi ^{4}, \end{aligned}$$

(4)

where the couplings can in general depend on the ratio of the two fields i.e., $\phi /\chi$. If for example, we assume the couplings to be independent of the ratio of the two fields and consider the spontaneous breaking of scale symmetry i.e., the case with $\langle \phi \rangle \ne 0,\,\langle \chi \rangle \ne 0$, thus, as a result of minimizing the potential, we arrive at [63]

$$\begin{aligned} \frac{\langle \phi \rangle }{\langle \chi \rangle }=-\frac{\lambda _{m}}{\lambda _{\phi }},\quad V_1=\frac{\lambda _{\chi }}{4}\left( \chi ^{2}+\frac{\lambda _{m}}{\lambda _{\chi }} \phi ^{2}\right) ^{2}, \end{aligned}$$

(5)

with $\lambda _{m}^{2}=\lambda _{\phi }\lambda _{\chi }$ and $\lambda _{m}<0$.

In (5) we can re-define the coupling as

$$\begin{aligned} \bar{\lambda }_{\chi }=\lambda _{\chi }\left( 1+\frac{\lambda _{m}}{\lambda _{\chi }} \frac{\phi ^{2}}{\chi ^{2}}\right) ^{2}, \end{aligned}$$

(6)

then the potential (5) looks like a simple quartic potential

$$\begin{aligned} V_{1}=\frac{\bar{\lambda }_{\chi }}{4}\chi ^{4}. \end{aligned}$$

(7)

We can alternatively have a potential of the form

$$\begin{aligned} V_{2}=\frac{\tilde{\lambda }_{\phi }}{4}\phi ^{4}\,,\quad \tilde{\lambda }_{\phi } =\lambda _{\phi }\left( 1-\frac{\phi ^{2}}{\chi ^{2}}\right) ^{2}, \end{aligned}$$

(8)

which also satisfies the constraint (3) and is different from (4). We will later see that the form of the potential in (8) gives a viable inflationary scenario. From (5)–(8) we can crucially learn how to define couplings as a function of the ratio of two fields in a scale invariant model. Of course, we only considered here simple toy models. However, we note that such field dependent couplings can be expected to arise in string theory and were applied in the context of early Universe [64].

The spontaneous breaking of scale symmetry occurs when one of the fields develops a VEV (let us take the field $\chi$) which induces the emergence of a corresponding massless Goldstone boson (dilaton) $\tilde{\chi }=\sqrt{6}M\ln \left( \frac{\chi }{\sqrt{6}M}\right)$ that is associated with an arbitrary scale $M\propto m_\mathrm{P}$ [42]. By performing a Weyl rescaling of the metric $g_{\mu \nu }\rightarrow \tilde{g}_{\mu \nu }=\left( \frac{\chi }{\sqrt{6}M}\right) ^{2}g_{\mu \nu }$ and $\phi \rightarrow \tilde{\phi }=\frac{M}{\sqrt{6}\chi }\phi$ we indeed observe that the field $\tilde{\chi }$ is massless since the potential becomes independent of the field $\tilde{\chi }$

$$\begin{aligned} V\left( \phi ,\,\chi \right) =\phi ^{4}f\left( \frac{\phi }{\chi }\right) =\tilde{\phi }^{4}f\left( \frac{\tilde{\phi }}{M}\right) . \end{aligned}$$

(9)

Although interesting cosmology and particle physics can be developed based on the scale invariant models, we need to constrain the implications of the massless dilaton present in the system [46]. It was shown that the dilaton can be gauged away if we consider a model with local scale symmetry [65].

2.2 Conformal invariance

A general action that is invariant under local scale transformations $g_{\mu \nu }\rightarrow \Omega ^{-2}\left( x\right) g_{\mu \nu }\,,\,\phi \rightarrow \Omega (x)\phi ,\, \chi \rightarrow \Omega (x)\chi$ can be written as

$$\begin{aligned} S_{local}= & {} \int d^{4}x\,\sqrt{-g}\Bigg [\frac{\left( \chi ^{2}-\phi ^{2}\right) }{12}R +\frac{1}{2}\partial ^{\mu }\chi \partial _{\mu }\chi \nonumber \\&\quad -\frac{1}{2}\partial ^{\mu } \phi \partial _{\mu }\phi -\phi ^{4}f\left( \frac{\phi }{\chi }\right) \Bigg ], \end{aligned}$$

(10)

where the potential in the above action should also satisfy the condition (3).

From the above action we can define an effective Planck mass $m_{eff}^{2}=\frac{\chi ^{2}-\phi ^{2}}{6}$ which evolves with time. In these theories, we would recover the standard Planck scale $m_\mathrm{P}$ when the fields reach their VEV. Note that the field $\chi$ contains a wrong sign for the kinetic term but it is not a problem as we can gauge fix the field at $\chi =\text {constant}=\sqrt{6}M$ for all spacetime where $M\sim \mathcal {O}\left( m_\mathrm{P}\right)$. This particular gauge choice is so called $c-$gauge⁷ which spontaneously breaks the conformal symmetry. It was argued that the theories in this gauge are of interest especially in cosmological models based on particle physics [46]. We will further see in this paper that fixing the scale M sources the hierarchy of mass scales related to inflation and particle physics (e.g., neutrino masses). In the inflationary models based on GUTs it is natural that the field $\phi$ takes a non-zero VEV, i.e., $\langle \phi \rangle \ne 0$ in which case it is useful to assume $6M^{2}-\langle \phi \rangle ^{2}=6m_\mathrm{P}^{2}$ in order to generate Planck mass. Moreover, its also necessary to keep the evolution of the field $\phi \lesssim \sqrt{6}M$ in order to avoid an anti-gravity regime.

Considering $f\left( \frac{\phi }{\chi }\right) =\lambda \left( 1-\frac{\phi ^{2}}{\chi ^{2}}\right) ^{2}$ in (10), SBCS via gauge fixing $\chi =\sqrt{6}m_\mathrm{P}$ leads to the Einstein frame action in terms of a canonically normalized field $\phi =\sqrt{6}m_\mathrm{P}\,\tanh \left( \frac{\varphi }{\sqrt{6}m_\mathrm{P}}\right)$ and it is written as

$$\begin{aligned} S_{local}=\int d^{4}x\,\sqrt{-g}\left[ \frac{m_\mathrm{P}^{2}}{2}R -\frac{1}{2}\partial ^{\mu }\varphi \partial _{\mu }\varphi -\lambda m_\mathrm{P}^{4} \tanh ^{4}\left( \frac{\varphi }{\sqrt{6}m_\mathrm{P}}\right) \right] . \end{aligned}$$

(11)

We can see that the above action leads to a Starobinsky like inflation as the potential acquires a plateau when $\varphi \gg m_\mathrm{P}$ (i.e., $\phi \rightarrow \sqrt{6}m_\mathrm{P}$). In this case the inflaton rolls down to a zero VEV by the end of inflation because of the gauge fixing $\chi =\sqrt{6}m_\mathrm{P}$ and consequently Einstein gravity is recovered.

In the next sections, we will study realistic GUT inflationary models where the inflaton rolls down to non-zero VEV and sources interesting implications in particle physics sector.

3 Coleman–Weinberg GUT inflation

In this section we briefly review the Shafi–Vilenkin model [11, 66]. It is one of the first realistic model of inflation which was based on SU(5) grand unified theory (GUT) . In this framework a new scalar field $\phi$, a SU(5) singlet was considered and it weakly interacts with the GUT symmetry breaking field (adjoint) $\Sigma$ and fundamental Higgs field $H_{5}$. The tree level scalar potential is given by

$$\begin{aligned} \begin{aligned}&V\left( \phi ,\,\Sigma ,\,H_{5}\right) \\&\quad = \frac{1}{4}a\left( \text {Tr}\Sigma ^{2}\right) ^{2}+\frac{1}{2}b\text {Tr}\Sigma ^{4} -\alpha \left( H_{5}^{\dagger }H_{5}\right) \text {Tr}\Sigma ^{2}\\&\qquad +\frac{\beta }{4} \left( H_{5}^{\dagger }H_{5}\right) ^{2}\\&\qquad +\gamma H_{5}^{\dagger }\Sigma ^{2}H_{5}+\frac{\lambda _{1}}{4}\phi ^{4} -\frac{\lambda _{2}}{2}\phi ^{2}\text {Tr}\Sigma ^{2}+\frac{\lambda _{3}}{2}\phi ^{2} H_{5}^{\dagger }H_{5}. \end{aligned} \end{aligned}$$

(12)

where the coefficients $a,\,b,\,\alpha$ and $\beta$ are taken to be of the order of⁸ $g^{2}$, therefore the radiative corrections in $\left( \Sigma ,\,H_{5}\right)$ sector can be neglected. The coefficient $\gamma$ takes a relatively smaller value and $0<\lambda _{i}\ll g^{2}$ and $\lambda _{1}\lesssim \text {max}\left( \lambda _{2}^{2},\,\lambda _{3}^{2}\right)$.

The GUT field $\Sigma$ which is a $5\times 5$ matrix can diagonalized as

$$\begin{aligned} \begin{aligned} \Sigma _{i}^{j}&=\delta _{i}^{j}\sigma _{i}\,,\quad i,\,j=1,\ldots ,5\,\\ \sum _{i=1}^{5}\sigma _{i}&=0. \end{aligned} \end{aligned}$$

(13)

Various symmetry breaking patterns of $\text {SU}(5)$ were studied in [67], among which the one with $\text {SU}(5)\rightarrow \text {SU}(3)_{c}\times \text {SU}(2)_{L}\times \text {U}(1)_{Y}$ corresponds to

$$\begin{aligned} \langle \Sigma \rangle =\sqrt{\frac{2}{15}}\sigma .\text {diag}\left( 1,\,1,\,1,-\frac{3}{2},\,-\frac{3}{2}\right) , \end{aligned}$$

(14)

where $\sigma$ is scalar field that emerges from spontaneous breaking of $\text {SU}(5)$. Substituting it in (12) the equations of motion for the $\sigma$ field read

$$\begin{aligned} \Box \sigma +\frac{\lambda _{c}}{4}\sigma ^{3}-\frac{\lambda _{2}}{2}\sigma \phi ^{2}=0, \end{aligned}$$

(15)

where $\lambda _{c}=a+\frac{7}{15}b$. Taking $\lambda _{2}\ll \lambda _{c}$, the $\sigma$ field quickly evolves to its local minimum of the potential given by

$$\begin{aligned} \sigma ^{2}=\frac{2\lambda _{2}}{\lambda _{c}}\phi ^{2}\,, \end{aligned}$$

(16)

Adding the radiative corrections due to the couplings $-\frac{\lambda _{2}}{2}\phi ^{2}\text {Tr}\Sigma ^{2}$ and $\frac{\lambda _{3}}{2}\phi ^{2}H_{5}^{\dagger }H_{5}$, the effective potential of $\phi$ gets to the CW form given by [11, 66]

$$\begin{aligned} V_{eff}\left( \phi \right) =A\phi ^{4}\left[ \ln \left( \frac{\phi }{\mu }\right) +C\right] +V_{0}, \end{aligned}$$

(17)

where

$$\begin{aligned} A=\frac{\lambda _{2}^{2}}{16\pi ^{2}}\left( 1+\frac{25}{16}\frac{g^{4}}{\lambda _{c}^{2}} +\frac{14}{9}\frac{b^{2}}{\lambda _{c}}\right) . \end{aligned}$$

(18)

The $\left( \phi \,,\,\sigma \right)$ sector of effective potential is given by

$$\begin{aligned} V_{eff}=\frac{\lambda _{c}}{16}\sigma ^{4}-\frac{\lambda _{2}}{4}\sigma ^{2}\phi ^{2} +A\phi ^{4}\left[ \ln \left( \frac{\phi }{\mu }\right) +C\right] +V_{0}.\nonumber \\ \end{aligned}$$

(19)

and $\mu =\langle \phi \rangle$ denotes the VEV of $\phi$ at the minimum, $V_0$ and C are dimensionfull and dimensionless constants respectively. Substituting (16) in (19) we obtain the effective potential for the field $\phi$ in the direction of $\sigma \propto \phi$. We set $V_{0}=\frac{A\mu ^{4}}{4}$ which is the vacuum energy density i.e., $V\left( \phi =0\right)$ and the constant C can be chosen such that $V\left( \phi =\mu \right) =0$. Therefore, the potential (19) can be written as

$$\begin{aligned} V_{eff}=A\phi ^{4}\left[ \ln \left( \frac{\phi }{\mu }\right) -\frac{1}{4}\right] +\frac{A\mu ^{4}}{4}. \end{aligned}$$

(20)

Following (16) the GUT field $\sigma$ reaches its global minimum only when the inflaton field reaches its VEV by the end of inflation. The inflationary predictions of this model were reported in detail in [13, 14]. This model was shown to be in good agreement with the spectral index $n_{s}=0.96-0.967$ and the tensor to scalar ratio $0.02\le r\le 0.1$, which is well consistent with the Planck 2015 data [6, 15].

From the VEV of the singlet field $\phi$ we can compute the masses of superheavy gauge bosons as

$$\begin{aligned} M_{X}=\sqrt{\frac{5\lambda _{2}g^{2}}{3\lambda _{c}A^{1/2}}}V_{0}^{1/4}. \end{aligned}$$

(21)

Taking $A\sim \frac{\lambda _{2}^{2}}{16\pi ^{2}}$ the mass of gauge bosons are approximately $2\sim 4$ times larger than the scale of vacuum energy $\left( V_{0}^{1/4}\right)$. The key prediction of GUT models is proton decay $\left( p\rightarrow \pi ^{0}+e^{+}\right)$ mediated by $X,\,Y$ gauge bosons. The life time of proton can be computed using

$$\begin{aligned} \tau _{p}=\frac{M_{X}^{4}}{\alpha _{G}^{2}m_{pr}^{5}}, \end{aligned}$$

(22)

where $m_{pr}$ is proton mass and $\alpha _{G}\sim 1/40$ is the GUT coupling constant. The current lower bound on proton life time is given by $\tau _{p}>1.6\times 10^{34}$ years indicates $M_{X}\sim 4\times 10^{15}\,\text {GeV}$ [68, 69].

4 GUT inflation with conformal symmetry

As discussed in Sect. 2, conformal symmetry is useful to generate flat potentials and the hierarchy of mass scales. Therefore, embedding conformal symmetry in GUT inflation is more realistic and helpful to generate simultaneously a Planck scale $m_\mathrm{P}$ along with the mass scale of X Bosons $M_{X}\sim 10^{15}\,\text {GeV}$ that sources proton decay. In this section, we extend the previously discussed CW inflation by means of introducing conformal symmetry in SU(5) GUT theory. We then obtain an interesting model of inflation by implementing spontaneous breaking of conformal symmetry together with GUT symmetry.⁹ We start with two complex singlet fields¹⁰ of $\text {SU}(5)$ $\left( \Phi ,\,\bar{X}\right)$ where the real part of $\Phi$ ($\phi =\sqrt{2}\mathfrak {Re}\left[ \Phi \right]$) is identified as the inflaton. Gauge fixing the field $\bar{X}$ causes SBCS as discussed in Sect. 2. It is worth to note here that the same framework we study here, based on $\text {SU}(5)$ GUT, can be easily realized in the $\text {SO}(10)$ GUT. Therefore, the two complex singlets of $\text {SU}(5)$ considered here are also singlets of $\text {SO}(10)$ [14, 24].

The conformally invariant action with complex SU(5) singlet fields $\left( \Phi ,\,\bar{X}\right)$ can be written as

$$\begin{aligned} S_{G}= & {} \int d^{4}x\,\sqrt{-g}\Bigg [\left( \vert \bar{X}\vert ^{2} -\vert \Phi \vert ^{2}-\text {Tr}\Sigma ^{2}\right) \frac{R}{12}\nonumber \\&\quad -\frac{1}{2} \left( \partial \Phi \right) ^{\dagger }\left( \partial \Phi \right) +\frac{1}{2} \left( \partial \bar{X}\right) ^{\dagger }\left( \partial \bar{X}\right) \nonumber \\&\quad -\frac{1}{2}\text {Tr}\left[ \left( D^{\mu }\Sigma \right) ^{\dagger } \left( D_{\mu }\Sigma \right) \right] -\frac{1}{4}\text {Tr}\left( \varvec{F}_{\mu \nu } \varvec{F}^{\mu \nu }\right) \nonumber \\&\quad -V\left( \Phi ,\,\bar{X},\,\Sigma \right) \Bigg ], \end{aligned}$$

(23)

where $D_{\mu }\Sigma =\partial _{\mu }\Sigma -ig\left[ \varvec{A}_{\mu },\,\Sigma \right]$, $\varvec{A}_{\mu }$ are the 24 massless Yang-Mills fields with Field strength defined by $\varvec{F}_{\mu \nu }\equiv \varvec{\nabla }_{[\mu }\varvec{A}_{\nu ]}-ig\left[ \varvec{A}_{\mu },\,\varvec{A}_{\nu }\right]$. Here we assume the $\Phi$ field coupling to the Higgs field $H_{5}$ is negligible and not very relevant during inflation. We consider that the singlet field $\Phi$ is weakly coupled to the adjoint field $\Sigma$ through the following tree level potential

$$\begin{aligned} V\left( \Phi ,\,\bar{X},\,\Sigma \right)= & {} \frac{1}{4}a\left( \text {Tr} \Sigma ^{2}\right) ^{2}+\frac{1}{2}b\text {Tr}\Sigma ^{4}\nonumber \\&-\frac{\lambda _{2}}{2} \vert \Phi \vert ^{2}\text {Tr}\Sigma ^{2}f\left( \frac{\Phi }{\bar{X}}\right) {+}\frac{\lambda _{1}}{4}\vert \Phi \vert ^{4}f^{2} \left( \frac{\Phi }{\bar{X}}\right) \!\!,\nonumber \\ \end{aligned}$$

(24)

where the coefficients $a\sim b\sim g^{2}$ (gauge couplings $g^{2}\sim 0.3$). Following the discussion in Sect. 2 we assume the coupling constants are field dependent, i.e., in (24) the coupling constants can be read as $\tilde{\lambda }_{2}=\lambda _{2}f\left( \frac{\Phi }{\bar{X}}\right) ,\, \tilde{\lambda }_{1}=\lambda _{1}f^{2}\left( \frac{\Phi }{\bar{X}}\right)$ which depend on the ratio of the fields $\left( \Phi ,\,\bar{X}\right)$. We consider

$$\begin{aligned} f\left( \frac{\Phi }{\bar{X}}\right) =\left( 1-\frac{\vert \Phi \vert ^{2}}{\vert \bar{X}\vert ^{2}}\right) . \end{aligned}$$

(25)

With the tree level potential in (24), the action (23) is conformally invariant under the following transformations

$$\begin{aligned}&g_{\mu \nu }\rightarrow \Omega \left( x\right) ^{2}g_{\mu \nu },\quad \bar{X}\rightarrow \Omega ^{-1}\left( x\right) \bar{X},\nonumber \\&\Phi \rightarrow \Omega ^{-1}\left( x\right) \Phi ,\quad \Sigma \rightarrow \Omega ^{-1}\left( x\right) \Sigma . \end{aligned}$$

(26)

The SBCS occurs with gauge fixing $\bar{X}=\bar{X}^{*}=\sqrt{3}M$, where $M\sim \mathcal {O} \left( m_\mathrm{P}\right)$. We assume inflation to happen in a direction $\text {I}m\Phi =0$. Therefore, for the stability of inflaton trajectory we require the mass of $\text {I}m\Phi$ to be¹¹ $m_{\text {Im}\Phi }^{2}\gg H_{inf}^{2}$. To arrange this, we can add a new term to the potential (24) as

$$\begin{aligned} V_{S}=V\left( \Phi ,\,\bar{X},\,\Sigma \right) +\frac{\lambda _{im}}{4} \left( \Phi -\Phi ^{\dagger }\right) ^{2}\left( \Phi +\Phi ^{\dagger }\right) ^{2}, \end{aligned}$$

(27)

such that the mass of the $\text {Im}\Phi$ in the inflationary direction is $m_{\text {Im}\Phi }^{2}=\frac{\partial ^{2}V_{S}}{\partial \text {Im}\Phi ^{2}}=\lambda _{im}\left( \Phi +\Phi ^{*}\right) ^{2}$. Therefore, if $\lambda _{im}\gg \lambda _{1,2}$ we can have $m_{\text {Im}\Phi }^{2}\Big \vert _{\text {Im}\Phi =0}\gg H_{inf}^{2}$ during inflation. In this way, we can successfully obtain the stability of the inflaton trajectory during inflation [73]. Note that when multiple non-minimally scalar fields are involved, it is in generally expected to induce geometrical destabilization effects due to the negative curvature of the fields space in the Einstein frame. This topic has been extensively studied in recent years [74,75,76,77,78,79]. In Appendix A, we present details of fields space geometry and argue that these effects might be negligible in the model we study herein, deferring a detailed quantitative analysis for future investigations. Similarly to the SV model, we also consider here $\text {SU}(5)\rightarrow \text {SU}(3)_{c}\times \text {SU}(2)_{L}\times \text {U}(1)_{Y}$ by

$$\begin{aligned} \langle \Sigma \rangle =\sqrt{\frac{1}{15}}\sigma .\text {diag} \left( 1,\,1,\,1,-\frac{3}{2},\,-\frac{3}{2}\right) . \end{aligned}$$

(28)

Likewise to the SV model, we assume $\lambda _{1}\ll \lambda _{2}\ll a,\,b$ and due to the coupling $-\frac{\lambda _{2}}{2}\phi ^{2}\text {Tr}\Sigma ^{2}f\left( \frac{\phi }{\sqrt{6}M}\right)$, the GUT field $\sigma$ reaches to its local field dependent minimum given by¹²

$$\begin{aligned} \sigma ^{2}=\frac{2}{\lambda _{c}}\lambda _{2}\phi ^{2}f\left( \frac{\phi }{\sqrt{6} M}\right) . \end{aligned}$$

(29)

Note that the above local minimum of the GUT field remains the same even though there is a non-minimal coupling with the Ricci scalar. We can easily understand this by conformally transforming the action (23) into the Einstein frame.

After SU(5) symmetry breaking, the X gauge bosons become superheavy, whereas the field $\sigma$ continues to follow the behavior of the field $\phi$. The tree level potential for $\left( \phi ,\,\sigma \right)$ sector is given by

$$\begin{aligned} V=\left[ \frac{\lambda _{c}}{16}\sigma ^{4} {-}\frac{\lambda _{2}}{4}\sigma ^{2}\phi ^{2}f\left( \frac{\phi }{\sqrt{6}M}\right) {+}\frac{\lambda _{1}}{4}\phi ^{4}f^{2}\left( \frac{\phi }{\sqrt{6}M}\right) \right] . \end{aligned}$$

(30)

Substituting (29) in (23) and rescaling the field $\phi \rightarrow \sqrt{1+\frac{\lambda _{2}}{\lambda _{c}}}\phi$, we obtain

$$\begin{aligned} S_{G}&=\int d^{4}x\,\sqrt{-g}\Bigg \{ \left( 6M^{2}-\phi ^{2}\right) \frac{R}{12} -\frac{1}{2}\left( \partial \phi \right) ^{2}\nonumber \\&-\left[ \frac{\lambda _{c}}{16}\sigma ^{4}-\frac{\bar{\lambda }_{2}}{4}\sigma ^{2} \phi ^{2} f\left( \frac{\phi }{\sqrt{6}M}\right) \right. \nonumber \\&\left. +\frac{\bar{\lambda }_{1}}{4} \phi ^{4}f^{2}\left( \frac{\phi }{\sqrt{6}M}\right) \right] \Bigg \}, \end{aligned}$$

(31)

where $\bar{\lambda }_{1,2}=\lambda _{1,2}\sqrt{\frac{1}{1+\frac{\lambda _{2}}{\lambda _{c}}}}$.

Since $\lambda _{1}\ll \lambda _{2}$, the effective potential for the inflaton field $\phi$ due to the radiative corrections becomes

$$\begin{aligned} V_{eff}\left( \phi \right) =V+\delta V+m_{\sigma }^{4}\ln \left( \frac{m_{\sigma }^{2}}{\mu ^{2}}\right) +V_{0}, \end{aligned}$$

(32)

where $\delta V$ is the counter term, $\mu$ is the VEV of the field $\phi$ and $V_{0}$ is a constant. Using (29), choosing an appropriate $\delta V=\frac{\delta \bar{\lambda }_{2}}{4}\sigma ^{2}\phi ^{2}f^{2} \left( \frac{\phi }{\sqrt{6}M}\right)$, a normalization constant such that $V_{eff}\left( \phi =\mu \right) =0$ and the vacuum energy density such that $V\left( \phi =0\right) =V_{0}=\frac{A\mu ^{4}}{4}$, we obtain

$$\begin{aligned} V_{eff}\left( \phi \right)= & {} A\phi ^{4}f^{2}\left( \frac{\phi }{\sqrt{6}M}\right) \nonumber \\&\ln \left( \left( \frac{6\phi ^{2}M^{2}f\left( \frac{\phi }{\sqrt{6}M}\right) }{\mu ^{2}m_\mathrm{P}^{2}}\right) -\frac{1}{4}\right) +\frac{A\mu ^{4}}{4},\nonumber \\ \end{aligned}$$

(33)

where $A\sim \frac{\bar{\lambda }_{2}^2}{16\pi ^{2}}$.

We note here that the CW potential we considered is the standard one obtained from 1-loop correction in Minkowski space-time. In the de Sitter background, 1-loop corrections are in principle different and their significance was discussed in literature [81,82,83]. Recently, in Ref. [84], it was argued that during slow-roll inflation we can neglect the contribution of 1-loop corrections in the gravity sector. In addition, the contributions from higher loops can also be neglected by the consideration of the slow-rolling scalar field. Refs. [85, 86] provide quantum corrections calculated for the cases of non-minimally coupled scalar fields.

In order to get a Planck mass $m_\mathrm{P}$ dynamically generated by the end of inflation, we should take the corresponding VEV of the inflaton field as

$$\begin{aligned} \langle \phi \rangle =\mu =\sqrt{6}M\sqrt{1-\frac{m_\mathrm{P}^{2}}{M^2}}. \end{aligned}$$

(34)

We can see that $M\ge m_P$ and $\mu \rightarrow \sqrt{6}M$ if $M\gg m_P$.

Taking the function $f\left( \frac{\phi }{\sqrt{6}M}\right)$ from (25) and by doing a conformal transformation of the action (31) with the effective potential (33) into Einstein frame, we obtain (expressing in the units of $m_\mathrm{P}=1$)

$$\begin{aligned} S_{G}^{E}= & {} \int d^{4}x\,\sqrt{-g_{E}}\left[ \frac{1}{2}R_{E}-\frac{1}{2M^{2} \left( 1-\frac{\phi ^{2}}{6M^{2}}\right) ^{2}}\partial ^{\mu }\phi \partial _{\mu }\phi \right. \nonumber \\&\left. -\frac{V_{eff}\left( \phi \right) }{36M^{4}f^{2}\left( \frac{\phi }{\sqrt{6}M}\right) }\right] . \end{aligned}$$

(35)

Under the conformal transformation, the mass scales in the Einstein frame must be redefined as $\mu ^{2}\rightarrow \mu ^{2}\left( 6M^{2}-\phi ^{2}\right) ^{-1}$. This is very much an equivalent procedure to the 1-loop analysis of Higgs inflation. See Refs. [87,88,89,90] for a detailed discussion on the equivalence between Jordan and Einstein frames which exactly matches, if we redefine the mass scales accordingly by conformal factor. Subsequently, substituting (33) in (35)

$$\begin{aligned} S_{G}^{E}= & {} \int d^{4}x\,\sqrt{-g}\Bigg \{ \frac{1}{2}R_{E}-\frac{1}{2M^{2}\left( 1 -\frac{\phi ^{2}}{6M^{2}}\right) ^{2}}\partial ^{\mu }\phi \partial _{\mu }\phi \nonumber \\&-A\phi ^{4}\left[ \ln \left( \frac{\phi ^{2}}{\mu ^{2}}\right) -\frac{1}{4}\right] -\frac{A\mu ^{4}}{4}\Bigg \}. \end{aligned}$$

(36)

The kinetic term of (36) is similar the no-scale models [37]. Canonically normalizing the scalar field as $\phi =\sqrt{6}M\tanh \left( \frac{\varphi }{\sqrt{6}}\right)$ yields the Einstein frame potential

$$\begin{aligned} V_{E}\left( \varphi \right)= & {} A\tanh ^{4}\left( \frac{\varphi }{\sqrt{6}}\right) \left( \ln \left( \frac{6M^2\tanh ^2\left( \frac{\varphi }{\sqrt{6}}\right) }{\mu ^2} \right) -\frac{1}{4}\right) \nonumber \\&+\frac{A\mu ^{4}}{4}. \end{aligned}$$

(37)

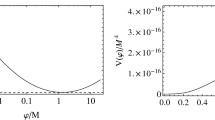
The corresponding VEV of the canonically normalized field is $\langle \varphi \rangle =\sqrt{6}\arctan \left( \frac{\mu }{\sqrt{6}M}\right)$. The potential in (37) is a flattened version of CW potential (20). Concretely, due to SBCS, the shape of the potential above VEV $\phi >\mu$ gets significantly flattened. In Fig. 1 we compare the CW potential of the SV model with the modified form (37) we obtained in our case. The shape of the potential reaches a plateau like in Starobinsky model when $\varphi \gg 1$ i.e., $\phi \rightarrow \sqrt{6}M$. Inflation always starts near the plateau and continues to evolve as $\phi \lesssim \sqrt{6}M$, therefore $f\left( \frac{\phi }{\sqrt{3}M}\right)$ defined in (25) is always positive and consequently that avoids an anti gravity regime. Note that the flat potential (37) is significantly different from the one of CW inflation, studied with positive non-minimal coupling in [17]. In the next subsection we show that the inflationary observables for the potential (37) exactly match those of Starobinsky and Higgs inflation.

Fig. 1

The dashed line denotes the CW potential in SV model. The full line indicates the shape of the potential obtained in (37) which comes from the insertion of conformal symmetry in SU(5). When $\varphi \gg \mu$ the above VEV (AV) branch of the potential approaches the plateau of Starobinsky model

4.1 Inflationary predictions and proton lifetime

We assume the standard Friedmann–Lemaître-Robertson–Walker (FLRW) background. Let us define the general definitions of slow-roll parameters as

$$\begin{aligned} \epsilon =\frac{H^{\prime }}{H},\quad \eta =-\frac{\epsilon ^{\prime }}{\epsilon },\quad \zeta =-\frac{\eta ^{\prime }}{\eta },\quad \delta =-\frac{\zeta ^{\prime }}{\zeta }, \end{aligned}$$

(38)

where H is the Hubble parameter and the prime $^{\prime }$ denotes derivative with respect to e-folding number $N=\ln a\left( t\right)$ before the end of inflation. The scalar power spectrum is given by

$$\begin{aligned} \mathcal{P}_{\mathcal {R}}=\frac{\gamma _{s}H^{2}}{8\pi ^{2}\epsilon }\Biggr |_{k=aH},\quad \gamma _{s}\equiv 2^{2\nu _{s}-3}\frac{\Gamma \left( \nu _{s}\right) {}^{2}}{\Gamma (3/2)^{2}}\left( 1-\epsilon \right) ^{2}. \end{aligned}$$

(39)

The scalar power spectrum amplitude at pivot scale $k=0.002\,Mpc^{-1}$ is measured to be $P_{\mathcal {R}_{*}}=2.2\times 10^{-9}$ [6]. The scalar spectral index up to the first orders in slow roll parameters is given by

$$\begin{aligned} n_{s}=1-2\epsilon -\eta . \end{aligned}$$

(40)

The running and running of running spectral index known as [91]

$$\begin{aligned} \begin{aligned} \alpha _{s}\equiv&\,\frac{dn_{s}}{d\ln k}\Biggr |_{k=aH}\simeq -2\epsilon \eta -\zeta \delta \,,\\ \beta _{s}\equiv&\, \frac{d\alpha _{s}}{d\ln k}\Biggr |_{k=aH}\simeq -2\epsilon \left( \eta +\zeta \right) -\eta \zeta \left( \zeta +\delta \right) . \end{aligned} \end{aligned}$$

(41)

The ratio of tensor to scalar power spectrum is

$$\begin{aligned} r=16\epsilon \Big \vert _{k=aH}. \end{aligned}$$

(42)

The potential (37) when $\varphi \gg 1$ (AV branch) can be approximated as

$$\begin{aligned} V_{E}\left( \varphi \right)\simeq & {} A\left( 1-e^{-\sqrt{2/3}\varphi }\right) ^{4} \ln \left( \frac{\sqrt{6}M\left( 1-e^{-\sqrt{2/3}\varphi }\right) }{\mu }\right) \nonumber \\\approx & {} A\left( 1-e^{-\sqrt{2/3}\varphi }\right) ^{4}\left[ \ln \left( \frac{\sqrt{6}M}{\mu }\right) \right. \nonumber \\&\left. -e^{-\sqrt{2/3}\varphi }+\mathcal {O}\left( e^{-\sqrt{\frac{2}{3}}\varphi }\right) ^2\right] . \end{aligned}$$

(43)

The equation of motion of the canonically normalized field is

$$\begin{aligned} \ddot{\varphi }+3H\dot{\varphi }+V_{E,\varphi }=0\,, \end{aligned}$$

(44)

which during the slow-roll regime reduces to

$$\begin{aligned} \begin{aligned}&\frac{\partial \varphi }{\partial N}\approx \frac{V_{E,\varphi }}{V_{E}}=\sqrt{\frac{2}{3}}\left( 4+\frac{1}{\ln \left( \frac{\sqrt{6}M}{\mu }\right) }\right) e^{-\sqrt{\frac{2}{3}}\varphi }\,\\&\quad \implies e^{\sqrt{\frac{2}{3}}\varphi (N_*)}= \frac{2}{3}\left( 4+\frac{1}{\ln \left( \frac{\sqrt{6}M}{\mu }\right) }\right) N_* \end{aligned} \end{aligned}$$

(45)

where we took $H_{inf}\approx \frac{V_{E}\left( \varphi \right) }{3}$ and $N_*$ is the 60 $e-$ foldings before the end of inflation. Computing the slow-roll parameter using (45) we obtain

$$\begin{aligned} \begin{aligned} \epsilon&= \frac{\partial \ln H}{\partial N}\approx \frac{1}{2}\left( \frac{V_{E,\varphi }}{V_{E}}\right) ^{2} \approx \frac{3}{4N^2}\,\\ \eta&=-\frac{\partial \epsilon }{\partial N}\approx \frac{2}{N}. \end{aligned} \end{aligned}$$

(46)

Using (46) we can write the predictions for the scalar tilt (40) and tensor to scalar ratio (42) as

$$\begin{aligned} n_{s}\approx 1-\frac{2}{N}\,,\quad r=\frac{12}{N^{2}}\,, \end{aligned}$$

(47)

which exactly match with the predictions of Starobinsky and Higgs inflation [1, 32]. We emphasize that the predictions of our model in (47) are almost independent of the VEV of the inflaton field $\langle \phi \rangle =\mu$.

In Table 1 we present the inflationary predictions of the model together with the corresponding X bosons mass and proton life time using (21) and (22). We also show our results for the case when the inflaton field rolls from above VEV (AV) i.e., when $\phi >\mu$. The predictions of below VEV (BV) branch i.e., when $\phi <\mu$ are not very interesting as those are nearly same in the original CW inflation without any conformal symmetry [14]. This is evident from Fig. 1 where we can see only the AV branch of the potential significantly different in our case, whereas the BV branch is nearly same as in the SV model. Therefore, our interest in this paper is restricted to AV branch. For this case, from Table 1 we can see that the inflationary predictions of the model almost remains the same for any value of inflaton VEV. Note that even though the inflaton field values are trans-Planckian, the values of $n_s$, r remain the same. This is due to the fact that when $\varphi \gg \mu$ the shape of the potential is exponentially flat like in Starobinsky model. Therefore, inflationary predictions only depend on the potential plateau rather than the field values (shift symmetry).

Table 1 Inflationary predictions of the AV branch solutions for different parameter values

In Fig. 2 we depict the evolution of field $\phi$ (also for the canonically normalized field $\varphi$) and slow-roll parameter $\epsilon$ for particular parameter values.

5 Type I seesaw mechanism and neutrino masses

In this section, we further extend our model through a type I seesaw mechanism with global lepton number symmetry, whose spontaneous breaking leads to the generation of neutrino masses. In this framework, we suppose the singlet field $\Phi$ carries two units of lepton number and is coupled to the three generation of singlet right handed Majorana neutrinos (RHNs), from [25]

$$\begin{aligned} V_{N}= & {} V\left( \Phi ,\,\bar{X},\,\Sigma \right) +Y_{D}^{ij}\bar{l_{L}^{j}}i \tau _{2}H^{\star }\nu _{R}^{i}\nonumber \\&+\frac{1}{2}Y_{N}^{i}\Phi f\left( \frac{\Phi }{\bar{X}}\right) \overline{\nu _{R}^{ic}}\nu _{R}^{i}+h.c, \end{aligned}$$

(48)

where l is the lepton doublet, $\tau _{2}$ is the second Pauli matrix. Here $Y_{D}$ is the Yukawa coupling matrix of the SM Higgs coupling to the left handed neutrinos and $Y_{N}$ is the coupling matrix of the singlet field to the three generations of Majorana RHNs $\left( \nu _{R}^{i}\right)$. In principle, we can also weakly couple the inflaton with the SM Higgs boson as

$$\begin{aligned} V_{h}=V_{N}+\lambda _{h}f\left( \frac{\Phi }{\bar{X}}\right) \Phi ^{\dagger }\Phi H^{\dagger }H. \end{aligned}$$

(49)

We note that even with the new potential in (49), conformal symmetry in (23) can be preserved by the following additional transformations¹³

$$\begin{aligned} l_{L}^{i}\rightarrow \Omega ^{3/2}l_{L}^{i}\,,\quad \nu _{R}^{i}\rightarrow \Omega ^{3/2}\nu _{R}^{i}\,,\quad H\rightarrow \Omega H \end{aligned}$$

(50)

Applying SBCS via $\bar{X}=\bar{X}^*=\sqrt{3}M$ and computing 1-loop corrections due to the additional couplings to neutrinos (48) and SM Higgs, the effective potential of the field $\phi$ becomes

$$\begin{aligned} V_{f}^{eff}= & {} \frac{36A_{f}M^{4}}{m_\mathrm{P}^{4}}f^{2}\left( \frac{\phi }{\sqrt{3}M}\right) \phi ^{4}\ln \left( \frac{\phi ^{2} f\left( \frac{\phi }{\sqrt{3}M}\right) }{\mu _{f}^{2}} -\frac{1}{4}\right) \nonumber \\&+\frac{A_{f}\mu _{f}^{4}}{4}\,, \end{aligned}$$

(51)

where $A_{f}=\frac{\beta _{f}}{32\pi ^{2}}$ and

$$\begin{aligned} \beta _{f}=20\bar{\lambda }_{2}^{2}+2\lambda _{h}^{2}+2\bar{\lambda }_{2} \sum _{i}\left( Y_{N}^{i}\right) ^{2}-\sum _{i}\left( Y_{N}^{i}\right) ^{4}. \end{aligned}$$

(52)

In (52) we assume the coupling constant $Y_{N}^{i}$ to be at least $\mathcal {O}\left( 10\right)$ smaller than $\bar{\lambda }_{2}$ and $\lambda _{h}\ll Y_{N}^{i}$, such that $\beta _{f}\sim 20\bar{\lambda }_{2}^{2}$ and $\mu _{f}\sim \mu$. Therefore, during inflation the coupling of a singlet field to the adjoint scalar $\Sigma$ dominates. Consequently, the inflationary predictions in Table 1 are unaffected by these additional couplings to Higgs and singlet neutrinos. Moreover, since we impose $\lambda _{h}\ll Y_{N}^{i}$, the inflaton field dominantly decays to RHNs rather than to SM Higgs.

Lets consider that the lepton number violation happens at a scale when $\langle \phi \rangle =\mu$. Computing the mass matrix of singlet and doublet neutrinos in the basis of $\nu _{L},\,\nu _{R}$, using the Einstein frame potential of (48), we have

$$\begin{aligned} \mathcal {M}_{\nu }=\left[ \begin{matrix}0 &{} Y_{D}v_{2}\\ Y_{D}^{T}v_{2} &{} \frac{m_\mathrm{P}^{2}}{M^{2}}\frac{\langle \phi \rangle Y_{N}}{\sqrt{2}} \end{matrix}\right] , \end{aligned}$$

(53)

where $v_{2}=246\,\text {GeV}$ is the electroweak vacuum. The light left handed neutrino mass can be obtained from perturbative diagonalization of (53) as

$$\begin{aligned} m_{\nu _{L}}\simeq \sqrt{2}Y_{D}Y_{N}^{-1}Y_{D}^{T}\frac{v_{2}^{2}}{\mu } \frac{M^{2}}{m_\mathrm{P}^{2}}. \end{aligned}$$

(54)

The mass of heavy RHNs is given by

$$\begin{aligned} m_{\nu _{R}}=\frac{Y_{N}\langle \phi \rangle }{\sqrt{2}}\frac{m_\mathrm{P}^{2}}{M^{2}}. \end{aligned}$$

(55)

The essence of the seesaw mechanism is the generation of neutrino masses, resulting in light left handed neutrinos and heavy right handed neutrinos. Both are related here to the VEV of the inflaton field.

Fig. 2

In the left panel we depict the evolution of the scalar field (in the units of $m_P$) during inflation versus the e-folding number. The solid blue line indicates the evolution of the canonically normalized field $\varphi$, whereas the dotted blue line is for the original field $\phi$. In the right panel we plot the corresponding slow-roll parameters $\epsilon ,\,\eta$ versus N. Inflation ends when $\epsilon ,\,\eta =1$. For both plots, we have taken $\mu =1.12\,m_\mathrm{P}$

The current Planck data indicates the sum of light neutrino masses constrained as $\sum m_{\nu _{i}}<0.23\,eV$ [92]. Therefore considering the light neutrino mass to be $m_{\nu _{L}}\sim \mathcal {O}(0.1)\,\text {eV}$, (54) gives a relation

$$\begin{aligned} Y_{N}\simeq 6\sqrt{2}Y_{D}^{2}\frac{10^{14}\,GeV}{\mu }\frac{M^{2}}{m_\mathrm{P}^{2}}, \end{aligned}$$

(56)

Taking $Y_{D}\sim \mathcal {O}\left( 10^{-1}\right)$ and from Table 1 imposing $\mu \sim 1.2\,m_\mathrm{P}-24.37\,m_\mathrm{P}$, we get $2.5\times 10^{-6}\lesssim Y_{N}^{i}\lesssim 1.0\times 10^{-5}$. This supports our previous assumptions after (52), that the couplings to the RHNs have a negligible effect for inflation. Our generalization of the SV model successfully fits into explaining the origin of neutrino masses. We can also take $Y_{D}<\mathcal {O}\left( 10^{-1}\right)$ which results in smaller values for $Y_{N}<\mathcal {O}\left( 10^{-6}\right)$. Taking $Y_{N}\sim 10^{-6}$, the heavy RHN mass will be around $m_{\nu _{R}}\sim 4\times 10^{12}\,\text {GeV}.$ For $Y_{N}<\mathcal {O}\left( 10^{-6}\right)$ we can lower the masses of RHNs. In the next section we aim to study reheating in our inflationary scenario, taking into account the constraints we have derived so far.

6 Reheating and non-thermal leptogenesis

We consider reheating through a dominant decay of the inflaton into heavy RHNs¹⁴$^{,}$¹⁵which requires $m_{\varphi }\gtrsim 2m_{\nu _{R}}$. The mass of the canonically normalized field $\varphi$ at the minimum of the potential is given by the second derivative of the potential (37)

$$\begin{aligned} m_{\varphi }=\sqrt{V_{\varphi ,\,\varphi }^{E}}\Big \vert _{\varphi =\langle \varphi \rangle }=2\times 10^{-6}\mu , \end{aligned}$$

(57)

where we have taken a value for $A\sim 5\times 10^{-12}$ from Table 1.

We implement the scheme of non-thermal leptogenesis proposed in [24, 98] which can give rise to baryogenesis through CP violating decays of RH Majorana neutrinos. In this section, we closely follow [27,28,29]. We consider:

• Hierarchical masses for RHNs $m_{\nu _{R}^{1}}\ll m_{\nu _{R}^{2}}\sim m_{\nu _{R}^{3}}$. To arrange this we require the coupling constants to be $Y_{N_{1}}\ll Y_{N_{2}}\sim Y_{N_{3}}$. We assume that the inflaton decays equally into the two heavy RHNs $\nu _{R}^{2,3}$ and the corresponding reheating temperature can be computed using [26, 27]

$$\begin{aligned} T_{R}=\left( \frac{90}{\pi ^{2}g_{*}}\right) ^{1/4}\sqrt{\Gamma _{\varphi } \left( \varphi \rightarrow \nu _{R}^{i}\nu _{R}^{i}\right) m_\mathrm{P}}, \end{aligned}$$

(58)

where $g_{*}=105.6$ is the number of relativistic degrees of freedom and the decay rate is given by

$$\begin{aligned} \Gamma _{\varphi }\left( \varphi \rightarrow \nu _{R}^{i}\nu _{R}^{i}\right) \simeq \frac{m_{\varphi }}{4\pi }\sum _{i=1}^{3}c_{i}^{2}\left( \frac{m_{\nu _{R}^{i}}}{m_\mathrm{P}}\right) ^{2}\left( 1-\frac{4m_{\nu _{R}^{i}}^{2}}{m_{\varphi }^{2}}\right) ^{3/2}. \end{aligned}$$

(59)

Fig. 3

In this plot we depict the reheating temperatures $T_{R}$ Vs. $m_{\varphi }$ for the values of couplings $Y_{N}^{2,3}\sim 10^{-8}-10^{-6}$

The masses of heavy RHNs are $m_{\nu _{R}^{2,3}}\sim \frac{Y_{N}^{2,3}}{\sqrt{2}}$, which for $Y_{N}^{2,3}\sim 10^{-8}-10^{-6}$ we have $m_{\nu _{R}^{2,3}}\sim 10^{10}-10^{12}$ GeV. In Fig. 3 we plot the possible reheating temperatures¹⁶ of our case taking $c_{1}\approx 0$ and $c_{2}=c_{3}=1$.

• The decays of RH Majorana neutrinos $\nu _{R}^{i}$ break the lepton number conservation and leads to CP violation. There are two decay channels

$$\begin{aligned} \Gamma _{i}:\nu _{R}^{i}\rightarrow H+l_{i}\,,\quad \bar{\Gamma }_{i}:\nu _{R}^{i}\rightarrow H^{\dagger }+\bar{l}_{i}, \end{aligned}$$

(60)

where H and l denote the Higgs field and the lepton doublets of the SM. The (lepton asymmetry generated by the CP violation) decay of $\nu _{R}^{i}$ is measured by the following quantity

$$\begin{aligned} \epsilon _{i}\equiv \frac{\Gamma _{i}-\bar{\Gamma }_{i}}{\Gamma _{i}+\bar{\Gamma }_{i}} \lll 1. \end{aligned}$$

(61)

CP asymmetry $\epsilon _{i}$ can be computed for the dominant decays of $\nu _{R}^{2,3}$ using [28, 103,104,105]

$$\begin{aligned} \epsilon _{i}= & {} -\frac{1}{8\pi }\frac{1}{\left( Y_{D}Y_{D}^{\dagger }\right) _{11}} \sum _{i=2,3}\text {Im}\left[ \left\{ \left( Y_{D}Y_{D}^{\dagger }\right) _{1i}\right\} ^{2}\right] \nonumber \\&\quad \left[ f\left( \frac{m_{\nu _{R}^{i}}^{2}}{m_{\nu _{R}^{1}}^{2}}\right) +g\left( \frac{m_{\nu _{R}^{i}}^{2}}{m_{\nu _{R}^{1}}^{2}}\right) \right] , \end{aligned}$$

(62)

where

$$\begin{aligned} f\left( y\right) =\sqrt{y}\left[ {-}1{+}\left( y+1\right) \ln \left( 1+\frac{1}{y}\right) \right] , g\left( y\right) {=}\,\frac{\sqrt{y}}{y-1}. \end{aligned}$$

(63)

Here, we only aim to constrain the range of values for $\epsilon _{i}$ leaving for future studies the explicit computation of constraining Yukawa matrix $Y_{D}^{ij}$ [27].

The lepton asymmetry is given by

$$\begin{aligned} \frac{n_{L}}{s}=\sum _{i=1}^{3}\epsilon _{i}\text {Br}_{i}\frac{3T_{R}}{2m_{\varphi }}, \end{aligned}$$

(64)

where $n_{L}$ is the difference between number of leptons and anti-leptons and s indicates the entropy density, $\text {Br}_{i}$ denotes the branching ratio

• The production of RH Majorana neutrinos happens non-thermally and sufficiently late so that the produced lepton asymmetry sources the baryon asymmetry at a later stage. This essentially requires $m_{\nu _{R}^{1}}\gtrsim T_{R}$ so that the later decay of lightest RH Majorana neutrino $\nu _{R}^{1}$ does not wash away the produced lepton asymmetry by the heavy ones. We assume there is an accidental $B-L$ conservation¹⁷ such that sphaleron process is active which brings a part of the above lepton asymmetry into the baryon asymmetry (see Refs. [106,107,108] for details). As the reheating temperature in our case is $T_{R}\sim 10^{6}-10^{9}\,\text {GeV}$ (see Fig. 3), we take $Y_{N}^{1}\sim 10^{-10}-10^{-9}$ such that $m_{\nu _{R}^{1}}\sim 10^{8}-10^{9}\,\text {GeV}$ . Therefore, with values $m_{\nu _{R}^{2,3}}\sim 10^{10}-10^{12}\,\text {GeV}$ , $m_{\nu _{R}^{1}}\sim 10^{8}-10^{9}\,\text {GeV}$ and $T_{R}\sim 10^{6}-10^{9}\,\text {GeV}$, we have met the conditions for successful leptogenesis which are $m_{\nu _{R}^{2}}\sim m_{\nu _{R}^{3}}\gg m_{\nu _{R}^{1}}$ and $m_{\nu _{R}^{1}}\gtrsim T_{R}$.

Baryon asymmetry is proportional to the lepton asymmetry as

$$\begin{aligned} \begin{aligned} \frac{n_{B}}{s}\simeq&\, \frac{28}{79}\frac{n_{L}}{s}\\ \simeq&\, \frac{42}{79}\sum _{i=1}^{3}\epsilon _{i}\text {Br}_{i}\frac{T_{R}}{m_{\varphi }}. \end{aligned} \end{aligned}$$

(65)

The baryon asymmetry which is measured by the ratio of the difference between the number of baryons minus the anti-baryons $n_{B}$ to the entropy density in the present Universe is constrained [92] in the following form

$$\begin{aligned} \frac{n_{B}}{s}=\left( 6.05\pm 0.06\right) \times 10^{-10}. \end{aligned}$$

(66)

Considering branching ratios $\text {Br}_{1}=0$ and $\text {Br}_{2}=\text {Br}_{3}=\frac{1}{2}$ with $\epsilon _{1}\ll \epsilon _{2}\sim \epsilon _{3}$, we have

$$\begin{aligned} \frac{n_{B}}{s}\approx \epsilon _{2}\frac{T_{R}}{m_{\varphi }}. \end{aligned}$$

(67)

From Fig. 3 we can read that $\frac{T_{R}}{m_{\varphi }}\sim 10^{-7}\sim 10^{-4}$ , which indicates the CP violation in the decay of RH Majorana neutrinos $\left( \epsilon _{i}\right)$ must be in the range $6\times 10^{-6}\lesssim \epsilon _{2,3}\lesssim 6\times 10^{-3}$ to have the observed baryon asymmetry.

7 Conclusions

Coleman–Weinberg inflation [11] has been a successful and realistic model based on GUT and is consistent with the current Planck data with $r\gtrsim 0.02$ [15]. In this work, we have further generalized the framework of CW inflation with an additional conformal symmetry. Spontaneous breaking of conformal symmetry is useful to create a hierarchy of mass scales, therefore it is natural to realize this symmetry in GUT models. In this respect, two complex singlet fields of $\text {SU}(5)$ or SO(10) were considered and are coupled to the GUT fields in a suitable manner. We have showed that this setup, upon spontaneous breaking of GUT and conformal symmetry, leads to an interesting inflationary scenario driven by the real part of the singlet field. In our model, the above VEV branch of CW potential gets flattened to a Starobinsky plateau, allowing for $n_{s}\sim 1-\frac{2}{N}$ and $r\sim \frac{12}{N^2}$ for $N\sim 50-60$ number of e-foldings. Therefore, our model is observationally fits with the same predictions of the Starobinsky and Higgs inflation. Moreover, the VEV of the inflaton affects the masses of the superheavy gauge bosons that mediate the proton decay. We calculated the corresponding estimates for the proton life time above the current lower bound from Super-K data as $\tau _{p}\left( p\rightarrow \pi ^{0}+e^{+}\right) >1.6\times 10^{34}$. In the next step, we introduced a coupling between the complex singlet field with the generation of three singlet RHNs, where the singlet field is assumed to carry two units of lepton number. We implemented a type I seesaw mechanism, where spontaneous symmetry breaking of global lepton number results in generating neutrino masses. We put an upper bound to the inflaton couplings to RHNs, assuming inflation is dominated by inflaton couplings to GUT field. For the non-thermal leptogenesis to happen, we have considered a dominant decay of the inflaton into some of the RHNs and obtained the corresponding reheating temperatures as $10^{6}\text { GeV}\lesssim T_{R}<10^{9}$ GeV. Furthermore, our proposed extension of CW inflation can be tested within future CMB and particle physics experiments [109].

In this work, we mainly restricted to a non-supersymmetric construction of GUT inflation with conformal symmetry. It would be interesting to consider this model in GUT based SUGRA framework with superconformal symmetries, which we defer for future investigations.

Geometry of fields space

In the action (23) we have primarily three fields $\left( \phi =\sqrt{2}\mathfrak {Re}\left[ \Phi \right] ,\, \tau =\text {Im}\left[ \Phi \right] ,\,\sigma \right)$ which are non-minimally coupled to the Ricci scalar.¹⁸ After a conformal transformation to the Einstein frame, all their kinetic terms get in general modified, therefore introducing a field space geometry [74]. In more detail, rewriting our action (23) in terms of the three fields $\left( \phi =\sqrt{2}\mathfrak {Re}\left[ \Phi \right] ,\, \text {Im}\left[ \Phi ,\right] , \sigma \right)$, we retrieve

$$\begin{aligned} S_G= & {} \int d^4x\sqrt{-g}\left[ \left( 6M^2-\phi ^2- \sigma ^2-\tau ^2\right) \frac{R}{12}\right. \nonumber \\&\left. -\frac{1}{2}\partial ^\mu \phi \partial _\mu \phi -\frac{1}{2}\partial ^\mu \sigma \partial _\mu \sigma \right. \nonumber \\&\left. -\frac{1}{2}\partial ^\mu \tau \partial _\mu \tau -V\left( \phi ,\,\tau ,\,\sigma \right) \right] , \end{aligned}$$

(A1)

where $V\left( \phi ,\,\tau ,\,\sigma \right)$ is the potential whose details are not relevant here. A conformal transformation of the action (A1) into the Einstein frame yields (expressing in the units of $m_P=1$)

$$\begin{aligned} S_E{=} \int d^4x \sqrt{{-}g} \left[ \frac{1}{2}R_E{-}\frac{1}{2}G_{IJ} \partial ^\mu \phi ^I\partial _\mu \phi ^J{-}\frac{V\left( \phi ,\tau ,\sigma \right) }{\Omega _1^2} \right] \!, \end{aligned}$$

(A2)

where $\Omega _1 = \left( 6M^2-\phi ^2- \sigma ^2-\tau ^2\right)$ and $G_{IJ}$ is the fields space metric

$$\begin{aligned} G_{IJ}= \frac{M^2}{2\Omega _1}\delta _{IJ}+ \frac{3}{2}\frac{M^2}{\Omega _1^2}\Omega _{1,I}\Omega _{1,J}, \end{aligned}$$

(A3)

where $\Omega _{1,I}= \frac{\partial \Omega _1}{\partial \phi ^I}$. The field metric (A3) provides the dynamics of the fields in the Einstein frame. Here we label $I, J= 1,\,2,\,3$ as $\phi , \tau , \sigma$, respectively. It was shown in [74, 75] that if the scalar curvature of fields space is negative it might lead to geometrical destabilization during or after inflation depending on the dynamics of inflaton and the heavy fields.

To make the analysis easy let us first analyse the two fields space $\left( \phi ,\,\tau \right)$ in the direction of

$$\begin{aligned} \sigma ^2 = \frac{2\lambda _{2}}{\lambda _c} \phi ^2 f\left( \frac{\phi }{\sqrt{6}M} \right) . \end{aligned}$$

(A4)

Let us consider $f\left( \frac{\phi }{\sqrt{6}} \right) = \left( 1-\frac{\phi ^2}{6M^2} \right)$. As discussed in Sect. 4 during the inflationary regime $\phi \rightarrow \sqrt{6}M$ and since we have assumed $\lambda _{2} \ll \lambda _c$, then we have $\sigma ^2\ll \phi ^2$. In this phase, action (A1) effectively reduces to

$$\begin{aligned} S_G\approx & {} \int d^4x \sqrt{-g} \left[ \left( 6M^2-\phi ^2-\tau ^2 \right) \frac{R}{12}-\frac{1}{2}\partial _\mu \tau \partial ^\mu \tau \right. \nonumber \\&\left. -\frac{1}{2}\partial ^\mu \phi \partial _\mu \phi - V\left( \phi ,\,\tau \right) \right] . \end{aligned}$$

(A5)

We can re-parametrize the fields as

$$\begin{aligned} \phi = \rho \sin \theta \, \quad \tau = \rho \cos \theta , \end{aligned}$$

(A6)

where $\theta = \tan ^{-1}\left( \frac{\phi }{\tau } \right)$. Note that inflaton trajectory considered in Sect. 4 corresponds to $\theta =0$. Substituting (A6) in the action (A5) we get

$$\begin{aligned} S_G\approx & {} \int d^4x\sqrt{-g}\left[ \left( 6M^2-\rho ^2 \right) -\frac{1}{2}\partial _{\mu }\rho \partial ^\mu \rho \right. \nonumber \\&\left. -\frac{1}{2}\rho ^2\partial ^\mu \theta \partial _\mu \theta - V\left( \rho ,\,\theta \right) \right] . \end{aligned}$$

(A7)

Conformally transforming the above action into the Einstein frame gives (in the units of $m_P=1$)

$$\begin{aligned} S_G\approx & {} \int d^4x\sqrt{-g}\left[ \frac{1}{2}R_E-\frac{1}{2M^2\left( 1-\frac{\rho ^2}{6M^2}\right) ^2}\partial _{\mu }\rho \partial ^\mu \rho \right. \nonumber \\&\left. -\frac{\rho ^2}{2\left( 6M^2-\rho ^2\right) }\partial ^\mu \theta \partial _\mu \theta - \frac{V\left( \rho ,\,\theta \right) }{\left( 6M^2-\rho ^2 \right) ^2} \right] . \end{aligned}$$

(A8)

The above action can be rewritten as the following, by introducing a field metric

$$\begin{aligned} S_G \approx \int d^4x\sqrt{-g}\left[ \frac{1}{2}R_E-\frac{1}{2}G_{IJ}\partial ^\mu \phi ^I\partial _\mu \phi ^J - \frac{V\left( \rho ,\,\theta \right) }{\left( 6M^2-\rho ^2 \right) ^2} \right] , \end{aligned}$$

(A9)

where

$$\begin{aligned} G_{IJ}=\left( \begin{array}{cc} \frac{36M^{2}}{\left( 6M^{2}-\rho ^{2}\right) ^{2}} &{} 0\\ 0 &{} \frac{1}{\left( 6M^{2}-\rho ^{2}\right) } \end{array}\right) . \end{aligned}$$

(A10)

Here $I,\,J=1,2$ for $\rho ,\,\theta$ respectively. Computing the Ricci tensor and Ricci scalar for the metric (A10) we obtain

$$\begin{aligned} \mathcal {R}_{IJ}= \left( \begin{array}{cc} -\frac{1}{2} &{} 0 \\ 0 &{} -\frac{1}{2} \sinh ^2\left( \frac{\rho }{\sqrt{2}}\right) . \end{array} \right) \,,\quad \mathcal {R}=-1. \end{aligned}$$

(A11)

Notice that the Ricci scalar associated to the fields space is negative and unit. It is very similar to several Starobinsky like models of inflation and $\alpha -$ attractor models of SUGRA,¹⁹ for which it was shown that geometrical destabilization could only occur towards the end of inflation [75]. The point to emphasize the following. With a suitable choice of potential for $\theta$, fields space geometrical effects on inflationary epoch can be heavily suppressed (see e.g., [110] for more details). However, in recent studies, effects of heavy fields during preheating epoch have been explored in multifield non-canonical, non-minimal models of inflation [79, 95,96,97, 111]. We opted to ignore such effects in our investigation and assume likewise that inflaton dominantly decays into the RHNs in Sect. 6. We leave for future an analysis of this interesting aspect.

Let us now consider the two fields space $(\phi ,\,\sigma )$ in the direction of $\text {Im}[\Phi ]=0$ (i.e., $\theta =0$)

$$\begin{aligned} S_G= & {} \int d^4x\sqrt{-g}\left[ \left( 6M^2-\phi ^2-\tilde{\sigma }^2\right) \frac{R}{12} - \frac{1}{2}\partial _\mu \phi \partial ^\mu \phi \right. \nonumber \\&\left. -\frac{1}{2}\partial _\mu \tilde{\sigma }\partial ^\mu \tilde{\sigma } -V\left( \phi ,\,\tilde{\sigma } \right) \right] \,, \end{aligned}$$

(A12)

where we have rescaled $\sigma \rightarrow \frac{\sigma }{\sqrt{2}}$. Computing the Ricci scalar associated to fields space $(\phi ,\,\tilde{\sigma })$ we obtain [74]

$$\begin{aligned} \tilde{\mathcal {R}} = \frac{72M^2}{\left[ 2\omega +6\left( \omega _{,\phi }^2+\omega _{,\tilde{\sigma }}^2 \right) \right] ^2}, \end{aligned}$$

(A13)

where $\omega = 6M^2-\phi ^2-\tilde{\sigma }^2$ and $\omega _{,\phi }= \frac{\partial \omega }{\partial \phi },\,\omega _{,\tilde{\sigma }}= \frac{\partial \omega }{\partial \tilde{\sigma }}$. We can clearly see that the Ricci scalar of fields space $\left( \phi ,\,\tilde{\sigma } \right)$ is positive and therefore geometric destabilization may not occur in this case during inflationary regime. Even though efficient particle production can occur in the models with a positive field space with sharp features [95, 96, 112,113,114].