Finite temperature Landau gauge lattice quark propagator

Abstract

The quark propagator at finite temperature is investigated using quenched gauge configurations. The propagator form factors are investigated for temperatures above and below the gluon deconfinement temperature $T_c$ and for the various Matsubara frequencies. Significant differences between the functional behaviour below and above $T_c$ are observed both for the quark wave function and the running quark mass. The results for the running quark mass indicate a link between gluon dynamics, the mechanism for chiral symmetry breaking and the deconfinement mechanism. For temperatures above $T_c$ and for low momenta, our results support also a description of quarks as free quasiparticles.

1 Introduction and motivation

The study of strong interactions including temperature and density effects has been driven both by the tentative to understand the QCD dynamics and a strong experimental program that involves various facilities. From the theory side, this research includes the computation of two-point correlation functions that provide information on spectra, transport properties and other fundamental properties such as the confinement mechanism. Herein, we will not consider the dependence on the density of the hadronic matter.

At low temperatures, quarks and gluons are confined particles and appear only as constituents of mesons and baryons. At sufficiently high temperatures or densities, quark and gluons are expected to become deconfined and behave as free quasiparticles in a new state of matter, the strong coupled quark gluon plasma. At extreme temperatures, due to asymptotic freedom, quarks and gluons can be considered as free particles.

This view of the quark and gluon dynamics for temperatures above the critical temperature $T_c$, where the deconfined phase transition takes place, is motivated by asymptotic freedom and lies at the heart of the quasiparticle description used to investigate the thermodynamical properties of hadronic matter for $T > T_c$. For temperatures above $T_c$ the perturbative approach of the hard thermal loop (HTL) expansion, see e.g. [1, 2] and [3, 4] for recent reviews, seems to be the framework to understand the dynamics of QCD. Furthermore, some of the HTL predictions have been confirmed by first principles non-perturbative lattice QCD simulations; an example being the behaviour of thermal masses with the temperature of the heat bath.

The standard approach to identify the confined and the deconfined phases relies on the Polyakov loop L which is related to the free energy of quarks $F_T$. At $T < T_c$, the renormalised L is small, $F_T$ is large, and quarks are confined particles. For temperatures above $T_c$, L approaches unit, $F_T \approx 0$, and quarks become free quasiparticles. The curve L(T) shows that the nature of the confined-deconfined transition is a cross-over for full QCD and first order for the pure Yang–Mills (quenched QCD) [5, 6]. If for full QCD the critical temperature is $T_c \sim 150$–160 MeV, for its quenched version one get $T_c \sim 270$ MeV. In what concerns gluon dynamics, for the quenched version of the theory, the consideration of quantities other than the Polyakov loop reproduce both the nature of the transition and the quoted value for the critical temperature, see e.g. [7].

One of the interests to study the quark and gluon two-point correlation functions with temperature comes from the connection between the propagators and confinement that can be linked, for example, by computing the corresponding spectral functions. If above $T_c$ quarks and gluons can be viewed as quasiparticles, their propagators should behave differently from the corresponding functions at temperatures below $T_c$.

The Landau gauge gluon propagator has been studied using non-perturbative methods for a wide range of temperatures both for full QCD and for the pure gauge theory [7,8,9,10,11,12]. These studies show that in the quenched theory the gluon propagator is sensitive to the breaking of center symmetry, that electric and magnetic mass scales are generated dynamically and the gluon thermal mass associated with the electric propagator scales with the temperature according to the prediction of hard thermal loop approach to QCD, namely $m_D \propto T$ above the critical temperature. Furthermore, the calculations performed using the continuum formulation of QCD or lattice QCD simulations for the pure gauge sector are in good agreement; see [13] and references therein. Moreover, the non-perturbative approaches suggest that HTL QCD is a good framework to describe the dynamics of QCD for $T \sim T_c$ and above. From these studies one can claim to have now a good picture for the gluon dynamics.

The Landau gauge quark propagator at finite temperature was also studied within the continuum non-perturbative approaches to QCD and using first principles lattice simulations.

The quark gap equation in the Landau gauge was solved relying on gluon propagators obtained from lattice simulations. The lattice data was fitted to a functional form that reproduces the perturbative tail at sufficiently high momenta [14,15,16,17]. In order to solve the Dyson–Schwinger equation for the quarks, the quark-gluon vertex was parameterised keeping only its tree level tensor structure, i.e. assuming $\varGamma _\mu \propto \gamma _\mu$ for the vertex, and, once more, ensuring the right perturbative tail at high momenta. The continuum studies have been focused on dynamical mass generation, through the computation of either the quark condensate [18], the running quark mass, the spectral function [19] at the chiral limit and order parameters for the deconfined phase transition. The form factors appearing in the quark propagator as function of the Matsubara frequencies, momentum and temperature have been only briefly reported but they show quite different behaviours above and below the critical temperature. How the various functions that appear in the quark propagator depend on the parameterisations introduced to solve the quark gap equation is not known and, therefore, these results care for further study or confirmation from independent calculations. The interest in the spectral functions at the chiral limit comes from knowing that at high temperature the quark propagator has two sets of poles, corresponding to an usual mass term and a collective plasmino mode, i.e. two different types of dispersion relations can be associated with this propagator [20]. Some authors also speculate on the presence of a third ultrasoft fermion mode that should appear in the quark propagator [19, 21, 22]. Evidence for a third mode for $T > T_c$ was also observed in Yukawa like models [23], on QED like models where it becomes an ultrasoft mode [24, 25] and in low energy effective models of QCD [26,27,28,29] where, again, the third mode is ultrasoft.

In what concerns continuum methods, the quark spectral function together with the quark self energy was computed within the framework of functional renormalization group [30]. The outcome reveals a spectral function with multiple peaks, whose details and number of maxima depend on the truncation used in the calculation.

The lattice quark propagator at finite temperature, in the Landau gauge, was computed for ${\mathscr {O}}(a)$-improved Wilson fermions using quenched gauge configurations by a number of authors [31,32,33,34,35,36,37,38]. The lattice studies have been focused either on the mass function and on the same spectral function as investigated by the continuum methods. For the quantities studied, at the qualitative level, lattice and continuum results are in good agreement. On the lattice the curve M / T as a function of the temperature, where M is the quark mass, has a discontinuity at $T_c$ but its behaviour for $T > T_c$ has not been resolved [37]. For Wilson fermions, the authors [31] found a linear grow of M / T above the transition temperature. However, given that there is some ambiguity in the definition of the quark mass and the poor agreement between the values of the Wilson fermion mass and the ${\mathscr {O}}(a)$-improved Wilson fermion mass, this result demands for confirmation. Furthermore, in what concerns the computation of the quark mass, a plateau associated to an effective quark mass was not always identified [31, 34] suggesting that instead one should consider a running quark mass. The lattice spectral function was computed and investigated assuming a multiple pole ansatz [32, 33, 35, 36, 38] that favours a pole structure associated with a thermal and a plasmino mode as predicted in [20]. The lattice calculations for the propagator used typically spatial physical volumes under ($\sim 2$ fm)$^3$ with two simulations performed using physical volumes ($\sim 3.5$ fm)$^3$ [35, 38] for $T/T_c = 0.55$ and 1.5 at the chiral limit.¹

In the current work we compute the lattice Landau gauge quark propagator at finite temperature with non-perturbatively ${\mathscr {O}}(a)$-improved Wilson fermions with gauge configurations generated with the Wilson action for the pure gauge theory. These configurations were used to investigate the lattice Landau gauge gluon propagator in [9]. As in this work, we take $T_c = 270$ MeV and consider temperatures above and below the critical temperature to study how different the propagator is in the confined and deconfined phase. Our main focus is in the calculation of the three form factors that determine the quark propagator at finite temperature and the running quark mass as a function of momentum and for the various Matsubara frequencies. By providing the form factors as a function of T, we aim to understand the differences between the two phases and provide information than can also be useful for the continuum approaches to QCD. No attempt is made to investigate any of the spectral functions that can be associated with the quark propagator.

The computations of the quark propagator reported below use lattices whose spatial physical volume is ($\sim 6.5$ fm)$^3$ and various lattice spacings around $a \sim 0.1$ fm. The lattice investigations of the Landau gauge gluon and ghost propagators at zero temperature [39,40,41], suggest that finite volume effects are under control in the sense that they are small and below the statistical precision of the simulations. We take as definition of the temperature the inverse length in the time direction and typically consider ratios of the spatial and time direction $L_s / L_t = 8$. Due to the anti-periodic boundary conditions along the time direction $p_4 = \pi \, T \, ( 2 \, n_t + 1 )$ where $n_t = 0, \, 1,\ldots$ and the spatial momenta are $p_i = 2 \, \pi \, T \, (L_t / L_s) \, n_i \approx 0.785 \, T \, n_i$ for $n_i = 0, \, 1,\ldots$ Furthermore, in order to experience the quark propagator at the chiral limit, we report on simulations using two values of the bare quark mass, namely $m_0 \approx 10$ MeV and 50 MeV.

Our results clearly show that the nature of the quark propagator form factors changes for temperature above $T_c$, compared with temperatures in the confined phase. This is reported with detail for both the quark wave function and the running quark mass. In particular, for the running quark mass we find that it is highly suppressed above $T_c$, with typical infrared values being about half of the corresponding values for the temperatures below $T_c$. Our computation is performed with quenched configurations and this results indicates that the gluon dynamics plays an important role in the mechanism of chiral symmetry breaking. A similar change in the functional form of the finite temperature gluon propagator form factors for temperatures above and below $T_c$ was observed also in lattice simulations [8, 9]. Indeed, these simulations show that the relative importance of its electric and magnetic components are inverted for $T \gtrsim T_c$, relative to confined phase, i.e. for small temperatures the electric form factor is larger than the magnetic one, while above $T_c$ the dominant form factor is associated with the gluon magnetic component.

The paper is organised as follows. In Sect. 2 we set the notation and definitions used throughout the current work and how the various form factors are measured. Furthermore, we detail the setup of the simulations analysed herein. In Sect. 3 we report our results for the various form factors prior to the estimation of the lattice artefacts for the two quark masses considered in the simulations. The study of the lattice artefacts and the definition of the running quark mass are detailed in Sect. 4.

Table 1 Lattice setup for the computation of the quark propagator in the quenched approximation. The coefficient $c_{sw}$ associated with the non-perturbative improvement of the simulations and $\kappa _c$ are taken from [43]. The bare quark mass $m_{bare}$ is computed using Eq. (9). T and $m_{bare}$ are given in MeV, the lattice spacing a is given in fm and the inverse of the lattice spacing 1 / a in GeV

2 The quark propagator and lattice setup

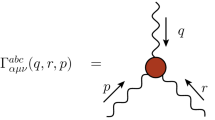
In the continuum, the quark propagator is diagonal in color space. At finite temperature, the presence of a thermal bath breaks rotational invariance, and the inverse of the space-spin quark propagator in momentum space reads

$$\begin{aligned}&S^{-1}(p_4 , \mathbf {p} ) \nonumber \\&\quad = i \gamma _4 \, p_4 ~ \omega (p_4, \mathbf {p}) + i \mathbf {\gamma } \cdot \mathbf {p} ~ Z(p_4 , \mathbf {p} ) + \sigma (p_4 , \mathbf {p} ) \end{aligned}$$

(1)

or, equivalently,

$$\begin{aligned}&S(p_4 , \mathbf {p} ) \nonumber \\&\quad = \frac{ - i \gamma _4 \, p_4 ~ \omega (p_4, \mathbf {p}) - i \mathbf {\gamma } \cdot \mathbf {p} ~ Z(p_4 , \mathbf {p} ) + \sigma (p_4 , \mathbf {p} ) }{ p^2_4 ~ \omega ^2 (p_4, \mathbf {p}) + \left( \mathbf {p}\cdot \mathbf {p} \right) ~ Z^2(p_4 , \mathbf {p} ) + \sigma ^2 (p_4 , \mathbf {p} ) }. \nonumber \\ \end{aligned}$$

(2)

Our analysis of the lattice propagator will assume that we are close to the continuum and, therefore, expressions (1) and (2) can be applied. The form factors $\omega$, Z and $\sigma$ can be accessed by computing traces of the propagator times gamma matrices.

Our calculation of the lattice quark propagator relies on the use of the non-perturbative ${\mathscr {O}}(a)$ improved clover action [42, 43] with tree-level ${\mathscr {O}}(a)$-improved sources [44,45,46]. The lattice quark propagator in real space reads

$$\begin{aligned} S(x,y) = \bigg ( 1 + 2 \, b_q \, a \, m \bigg ) ~ \left\langle ~ L(x) \, M^{-1}_{SW} (x,y) \, R(y) ~ \right\rangle , \end{aligned}$$

(3)

where $M^{-1}_{SW}$ stands for the inverse of the improved fermionic matrix, the rotated sources are given by

(4)

(5)

the left and right derivatives are

(6)

(7)

$U_\mu (x)$ stands for the gauge configuration, ${\hat{\mu }}$ is the unit vector associated with direction $\mu$ and a is the lattice spacing. For the coefficients associated with the improvement coming from the rotated sources we use their tree level values $b_q = c_q = 1/4$.

The momentum space propagator is obtained from Eq. (3) after a Fourier transformation. Recall that on the lattice the fermionic boundary conditions are periodic in the spatial directions and anti-periodic in time and the available space $\mathbf {p}$ and temporal $p_4$ momenta assume the following discrete values

$$\begin{aligned} p_4 = \frac{ \pi }{L_t} \, \left( 2 \, n + 1 \right) \qquad \text{ and } \qquad p_i = \frac{ 2 \, \pi }{L_s} \, n, \end{aligned}$$

(8)

where $n = 0, \, 1, \, 2,\ldots$

On the lattice the bare quark mass is given by

$$\begin{aligned} a \, m = \frac{1}{2} \left( \frac{1}{\kappa } - \frac{1}{\kappa _c} \right) , \end{aligned}$$

(9)

where the critical hopping parameter $\kappa _c$ depends on $\beta$, i.e. on the lattice spacing, and is defined as the value of $\kappa$ corresponding to a vanishing mass for the lightest pseudo-scalar meson. In the following we will use m as an indicator of how close the simulation is to the chiral limit. The $\kappa _c$ are taken from [47], interpolating their reported values when necessary.

The traces of propagator give us the form factors

$$\begin{aligned} \frac{ \omega (p_4, \mathbf {p})}{ p^2_4 ~ \omega ^2 (p_4, \mathbf {p}) + \left( \mathbf {p}\cdot \mathbf {p} \right) ~ Z^2(p_4 , \mathbf {p} ) + \sigma ^2 (p_4 , \mathbf {p} ) }, \end{aligned}$$

(10)

$$\begin{aligned} \frac{ Z(p_4 , \mathbf {p} )}{ p^2_4 ~ \omega ^2 (p_4, \mathbf {p}) + \left( \mathbf {p}\cdot \mathbf {p} \right) ~ Z^2(p_4 , \mathbf {p} ) + \sigma ^2 (p_4 , \mathbf {p} ) }, \end{aligned}$$

(11)

$$\begin{aligned} \frac{\sigma (p_4 , \mathbf {p} ) }{ p^2_4 ~ \omega ^2 (p_4, \mathbf {p}) + \left( \mathbf {p}\cdot \mathbf {p} \right) ~ Z^2(p_4 , \mathbf {p} ) + \sigma ^2 (p_4 , \mathbf {p} ) }, \end{aligned}$$

(12)

and by taking ratios of these functions one gets a continuum-like quark wave function and running quark mass defined by

$$\begin{aligned} Z_c(p_4, \mathbf {p}) = \frac{Z(p_4, \mathbf {p})}{\omega (p_4, \mathbf {p})} , \quad \text{ and } \quad M (p_4, \mathbf {p}) = \frac{\sigma (p_4, \mathbf {p}) }{ \omega (p_4, \mathbf {p})},\nonumber \\ \end{aligned}$$

(13)

respectively. Note that we use $\omega$ and not Z to define the ratios $Z_c$ and M because the simulation does not allow the computation of $Z(p_4, \mathbf {p} = 0)$.

For the computation of the Landau gauge quark propagator we use a subset of the quenched gauge configurations, rotated to the Landau gauge, generated for the work [9]. We refer the read to this paper for the details on the generation of the Wilson action pure gauge configurations, the rotation to the Landau gauge and on the scale setting for the conversion into physical units.² Furthermore, in order to minimise effects due to the breaking of the rotational invariance, we only report functions for momenta that verifies the cuts considered in [9] and introduced in [8]; see also [48]. In order to improve the signal to noise ratio we perform always a $Z_3$ average of the various lattice quantities; for example when reporting a quantity associated F with momenta $(p_4, p, 0, 0)$ it refers to $( F(p_4, p, 0, 0) + (p_4, 0, p, 0) + (p_4, 0, 0, p))/3$.

Fig. 1

The bare lattice form factors (10), (11), (12), in lattice units, as a function of $p = \sqrt{ p^2_4 + \mathbf {p}^2}$ for the various Matsubara frequencies. The $m_{bare} = 11$ MeV data for the smaller momenta has large fluctuations and some of the data points fall outside the range of the axis values. In the legend of the y axis, when reading $\omega$ it refers to definition given in Eq. (10), Z to Eq. (11) and $\sigma$ to Eq. (12)

Fig. 2

The same as in Fig. 1 but for $T = 260$ MeV

The statistical errors reported for the various quantities were computed using the bootstrap method with a confidence level of 67.5%. When reporting the ‘continuum” functions $Z_c$ and M, that are defined as ratios of traces of quark propagator multiplied by gamma matrices, an additional cut in the data surviving the momenta cuts is introduced to have a clear picture of the various functions and only the data whose relative error is below 50% is kept.

Fig. 3

The same as in Fig. 1 but for $T = 275$ MeV

Fig. 4

The same as in Fig. 1 but for $T = 305$ MeV

The lattice setup of the simulations reported below are given in Table 1. In all simulations, the results reported are for computations considering 100 gauge configurations rotated to the Landau gauge. Moreover, to increase the signal to noise ratio for all temperatures, with the exception of the highest, the quark propagator was computed for two point sources located at (0, 0, 0, 0) and $(L_t/2, 0, 0, 0)$ and the results averaged before performing any analysis. For the highest temperature the quark propagator was computed for a single source located at the origin of the lattice.

For pure gauge theory the deconfinement temperature happens at $T_c = 270$ MeV, see e.g. [7] and references therein. Our quark propagator simulations consider two temperatures below $T_c$, a temperature just above the critical temperature and three temperatures clearly above $T_c$. In all cases, with the exception of two temperatures, the quark propagator is computed for two bare quark masses $m_{bare} \approx 10$ and 50 MeV. In this way, one expects to reveal the fundamental properties of quark properties at finite temperature close to the chiral limit.

3 The lattice propagator

The lattice form factors (10), (11) and (12) are measured by taking traces of the lattice propagator times gamma matrices. Their behaviour as a function of $p = \sqrt{p^2_4 + \mathbf {p}^2}$ is illustrated in Figs. 1,  2,  3 and  4 for temperatures below and above the critical temperature $T_c = 270$ MeV and for all the Matsubara frequencies.

For the smallest bare quark mass and for the smallest temperature, the data shows large fluctuations but seems to follow the same pattern as the data for the heaviest bare quark mass. For the smallest $m_{bare}$ and T, due to the large fluctuations observed in particular at the lower momenta, some of data does not appear in the Fig. due our choice for the y scale. Around and above $T_c$ the behaviour of the form factors for the two $m_{bare}$ is quite similar. The Figs. also show a clear violation of the rotational symmetry, that translates into large differences in the various lattice form factors for the same value of four-momentum $p = \sqrt{ p^2_4 + \mathbf {p}^2}$ computed with different Matsubara frequencies, that occurs at all temperatures and that is particularly dramatic for (12).

Fig. 5

Bare lattice quark wave function $Z_c(p_4, \mathbf {p})$ for the first Matsubara frequency as a function of $p = \sqrt{p^2_4 + \mathbf {p}^2}$

Fig. 6

Running quark mass, in GeV, for the first Matsubara frequency as a function of $p = \sqrt{p^2_4 + \mathbf {p}^2}$. Recall that for $Z_c$ and M, besides the momentum cuts defined to reduce the lattice artefacts, all data points whose relative error is greater than 50% are ignored. This explains why some of the running mass plots are empty. It seems that M has larger fluctuations when compared to the quark wave function

The bare lattice quark wave function $Z_c (p_4, |\mathbf {p}|)$ for the full range of momenta, and the running quark mass $M (p_4, |\mathbf {p}|)$ for momenta up to 1.5 GeV can be seen in Figs. 5 and 6 for the first Matsubara frequency. Note that the data in the figures is not corrected for lattice spacing artefacts and that is the reason why for $M (p_4, |\mathbf {p}|)$ we only report data for small $p = \sqrt{ p^2_4 + \mathbf {p}^2}$. Indeed, the bare running quark mass at finite temperature looks like that observed at zero temperature as seen, for example, in Fig. 10 in [49]. This same Fig. also shows that up to momenta $a p \sim 0.5$ the lattice artefacts corrections are negligible or quite small. For the simulations reported here $a p \sim 0.5$ corresponds to a $p \sim 1$ GeV, see Table 1, and that is the reason why we plotted the running mass only up to $p = 1.5$ GeV. In this section, our analysis of the running quark mass refers only to its low momentum behaviour. The function $M (p_4, |\mathbf {p}|)$ for the full range of momenta is discussed in Sect. 4.

As Figs. 5 and 6 show, the quark propagator looks rather different below and above $T_c$. For high momenta, the quark wave function approaches a constant from above for $T < T_c$ and from below at $T > T_c$. Around the critical temperature the results favour a constant $Z_c$ for the full range of momenta accessed in our simulation. Figure 5 also shows that, for sufficiently high momenta, $\omega (p_4, \mathbf {p} ) \cong Z( p_4, \mathbf {p} )$, up to a constant factor close to unity. At low momenta $\omega (p_4, \mathbf {p} )$ exceeds $Z( p_4, \mathbf {p} )$ above the critical temperature, while $Z( p_4, \mathbf {p} )$ exceeds $\omega (p_4, \mathbf {p} )$ for temperatures below $T_c$. Note also that for temperatures above $T_c$ the quark wave function approaches a constant value from below, reproducing the same type of behaviour observed for zero temperature and in agreement with the predictions of perturbation theory.

Fig. 7

The lattice and HTL quark wave function at $T = 305$ MeV. The lattice data was rescaled to reproduce the HTL wave function at 3 GeV for $m_q = 200$ MeV (full symbols) and for $m_q = 400$ MeV (open symbols). Note that the data for $m_q = 50$ MeV and 100 MeV are indistinguishable in the plot

In order to compare our results with the predictions of the hard thermal loop (HTL) for the quark propagator, in Fig. 7 we show the lattice data together with the one loop HTL prediction for $Z_c (p_4, \mathbf {p} )$ and for $T = 305$ MeV, i.e. $T/T_c = 1.13$, for the first Matsubara frequency. We take the one loop HTL quark propagator from [50], and convert it to Euclidean space – see their Eqs. (5), (6) and (7). The exact definition of the quark mass that should appear in the HTL expressions is difficult to read directly from the lattice data, see Figs. 6 and 8, and we have included in the plot for the HTL quark wave function the corresponding numbers for various quark masses. Furthermore, we also show twice the same lattice data rescaled to reproduce the HTL function at $p = 3$ GeV for $m_q = 200$ MeV and for $m_q = 400$ MeV. As can be observed, at higher momenta, i.e. for $p = (\,p^2_4 + \mathbf {p}^2)^{1/2} \gtrsim 2$ GeV, the lattice data is in good agreement with HTL. In particular for $m_q = 400$ MeV the lattice quark wave function and the HTL function are in good agreement for the full range of momenta. Our conclusion being that for $T / T_c = 1.13$, the lattice data is in good qualitative agreement with HTL for the quark wave function.

Fig. 8

Running quark mass at the smallest momenta for the various T considered in the current work. Note that the smallest momenta is temperature dependent and ranges from $\sim 0.8$ GeV up to $\sim 1$ GeV. The vertical blue line identifies the gluon deconfinement transition

Similarly as for the quark wave function, the running quark mass shows the different behaviours above and below the deconfinement temperature (see Fig. 6). For temperatures below the critical temperature $M(p_4, \mathbf {p})$ is a decreasing function of $p = \sqrt{p^2_4 + \mathbf {p}^2}$, while above the deconfinement phase transition it becomes essentially constant. The observed behaviour of M for $T > T_c$ supports the interpretation of quarks as quasiparticles with a constant mass. Note, however, that for the largest temperature $M(p_4, \mathbf {p})$ seems to increase with p; see also the results reported in Sect. 4. For $T > T_c$ the constant quark mass is a function of the temperature and, for the range of T considered here, M decreases when T increases. This can be better viewed in Fig. 8, where $M(p_4, \mathbf {p} = 0)$ for the first Matsubara frequency is shown for the full range of temperatures considered in the current simulations. The values of $M(p_4, \mathbf {p} = 0)$ reported in Fig. 8 were computed using the data from the lowest momentum that fulfill the cuts mentioned before and taking the data of the lattice form factors (10), (11), (12) with the errors computed assuming Gaussian error propagation, i.e. we set $M(p_4, \mathbf {p} = 0) = \sigma (p_4, \mathbf {p} = 0) / \omega (p_4, \mathbf {p} = 0)$ and take for the statistical error

$$\begin{aligned} \varDelta M(p_4, 0)= & {} \sqrt{ \left( \frac{ \varDelta \sigma (p_4, 0) }{ \omega (p_4, 0)} \right) ^2 + \left( \frac{ \sigma (p_4, 0) \, \varDelta \omega (p_4, 0) }{ \omega ^2 (p_4, 0)} \right) ^2}\nonumber \\ \end{aligned}$$

(14)

where $\varDelta \sigma (p_4, 0)$ and $\varDelta \omega (p_4, 0)$ stand for the statistical errors in $\sigma (p_4, 0)$ and $\omega (p_4, 0)$, respectively, and $p_4$ should be understood as the first Matsubara frequency. Note that the values reported in Fig. 8 do not refer exactly to the same $p_4$, that ranges from just above $\sim 0.83$ GeV to just below $\sim 1.1$ GeV. It follows that for $T > T_c$ typical values for the mass of the quasiparticle are about $\sim 100$ MeV.

Although our simulations are not at the chiral limit, the data for the running mass clearly shows a strong mass suppression as the temperature crosses $T_c$, with the values of M given in Fig. 8 above $T_c$ being about half of the values reported when the quarks are in the confined phase.

4 On the correction of the lattice artefacts

As discussed in [45, 46] for the zero temperature case, the lattice form factors computed directly from the inversion of the fermion matrix are contaminated by lattice artefacts. The solutions suggested to remove the lattice artefacts rely on the tree level lattice quark propagator [45, 46], on an expansion in the invariants of the H4 group [54, 55] or on a combination of both methods [49].

In what concerns the quark wave function at finite temperature, i.e. the results reported in Sect. 3 and summarized in Fig. 5, the function $Z_c(p_4,\mathbf {p})$ looks rather flat for momenta above $\sim 2$ GeV for the temperatures investigated. This is precisely the type of functional behaviour predicted by perturbation theory. However, these findings for $Z_c(p_4,\mathbf {p})$ contrast with the results of previous simulations at zero temperature, where for sufficiently high momenta the lattice quark wave function is a decreasing function of p, even after the partial removing of the lattice artefacts based on the rotated tree level quark propagator [45, 46, 49]. These results follow because $Z_c(p_4,\mathbf {p})$ is measured as a ratio of functions that, according to the procedure mentioned above, have exactly the same type of lattice artefacts corrections and, therefore, by taking ratios of these type of functions the lattice artefacts cancel exactly or, at least, are strongly suppressed. Given the good agreement between the lattice $Z_c(p_4,\mathbf {p})$ reported in Fig. 5 and the results of perturbation theory for $p \gtrsim 2$ GeV, we assume that the computed $Z_c(p_4,\mathbf {p})$ are essentially free of lattice artefacts.

On the other hand, the running quark mass at finite temperature is computed as in the zero temperature case. Not surprisingly, the lattice data for $M(p_4, \mathbf {p})$ shows a similar pattern as observed at zero temperature and this function increases at higher momenta as observed in Figs. 1 and 10 of [49] for the uncorrected lattice data. It follows that the computation of the running quark mass requires an estimation and subtraction of the lattice artefacts.

For the estimation of the lattice artefacts for the running mass we use the procedure outlined in [45, 46]. The space-spin components of the rotated tree-level quark propagator are given by

(15)

Expressions for A(m, p) and B(m, p) can be found in [45, 46]. There is no unambiguous way to subtract the lattice artefacts. Typically, two main definitions of the “continuum” running mass are considered where one naïvely subtracts part of the lattice artefacts, defining $m_s ( p_4, \mathbf {p})$, and the so-called hybrid scheme that defines $m_h ( p_4, \mathbf {p})$, where in the subtraction of the lattice artefacts it is taking into consideration if the corrections give either positive or negative contributions to the pole mass. In the definition of $m_h ( p_4, \mathbf {p})$ the negative contributions are subtracted before rescaling the result to take into account the remaining corrections. Details of the procedure and definitions can be found in the above cited works. To illustrate the running quark mass definition, in Fig. 9 we report results obtained with the rotated tree level quark propagator, where the naïve pole mass grows with momenta and $m_h ( p_4, \mathbf {p})$ is constant for all ap.

Fig. 9

Tree level propagator mass for three momenta $\mathbf {p}$ being along the diagonal of the axis of the lattice. The data reported was computed for $T = 305$ MeV in a $80^3 \times 8$ lattice, $\kappa = 0.1348$ that corresponds to $m_{bare} = 53$ MeV, and for the first Matsubara frequency. The data referred as “Pert.” is the naïve tree level pole mass appearing in the rotated quark propagator. The data labelled as “Hyb.” is the tree level corrected result for the so-called hybrid definition of the mass. See [45, 46, 49] for details

Fig. 10

The running quark mass $m_h ( p_4, \mathbf {p})$ for all the T and for the simulations using $m_{bare} \sim 50$ MeV. Only the data corresponding to the first Matsubara frequency is shown

Fig. 11

The running quark mass $m_h ( p_4, \mathbf {p})$ for all the T and for all Matsubara frequencies computed for the simulations using $m_{bare} \sim 50$ MeV

The hybrid running quark mass for the simulations with a $m_{bare} \approx 50$ MeV and all temperatures are given in Fig. 10 for the first Matsubara frequency. The functional form at small momenta for $m_h( p_4, \mathbf {p})$ changes dramatically when the deconfinement transition is approached. At the infrared scales $m_h$ is a decreasing function of p for $T \lesssim T_c$, is essentially constant for T above $T_c$ and in the range 290–305 MeV and for the highest temperature considered here $m_h$ is an increasing function of the momenta. We call the reader’s attention that in the simulation for $T = 324$ MeV the number of lattice points in the time direction, used to define the temperature, is shorter $L_t = 6$ compared with all other cases that use $L_t = 8$. It is not clear if such a short time direction is responsible for the different observed behaviour in the hybrid running quark mass. At sufficiently high p, the data shows that the running masses seem to collapse into a single curve. The data reported in Fig. 10 suggests that at high p and within the range of momenta accessed in our simulation $m_h(p_4, \mathbf {p})$ is a decreasing function of p. We have tried to fit a constant value to the highest momenta and have verified that for $p \gtrsim 10$ GeV the lattice data for $m_h(p_4, \mathbf {p})$ is compatible with a constant just above 50 MeV; for example, for $T = 290$ MeV, we get $m_h = 51.984 \pm 0.030$ MeV with a $\chi ^2/d.o.f = 1.1$ for $p > 9.8$ GeV. This fit value for the mass is within the same range of values for $m_{bare}$ considered here – see Table 1.

For completeness, in Fig. 11 we show $m_h(p_4, \mathbf {p})$ for all temperatures and all the Matsubara frequencies. The data shows, once more, a clear violation of rotational symmetry.

The computed quark wave function $Z_c(p_4, \mathbf {p})$ and running quark mass $m_h(p_4, \mathbf {p})$ imply changes in the functional behaviour of the quark spectral functions below and above the critical temperature. However, given the small number of Matsubara frequencies accessed in our study, we do not attempt to compute any of the components of the quark spectral function.

5 Summary and conclusions

In the current work we report on the computation of the finite temperature Landau gauge lattice QCD quark propagator in the quenched approximation at small quark masses $\sim 10$ MeV and $\sim 50$ MeV for temperatures below and above the deconfinement phase transition. The various quark form factors are investigated as a function of the temperature for the various Matsubara frequencies.

Our results show that both the quark wave function and the running quark mass have different functional forms for $T < T_c$ and for $T > T_c$. Above $T_c$ the quark wave function seems to reproduce the predictions of HTL expansion for $T / T_c \gtrsim 1.1$ being constant for $p \gtrsim 2$ GeV and slightly suppressed at smaller momenta. The suppression of the quark wave function at infrared scales is also observed for the zero temperature case; see [49] and references therein. On the other hand, at low momenta and for $T < T_c$ the quark wave function is enhanced. These results show that $Z_c$ has a non-trivial dependence on the temperature and its suppression or enhancement at low momenta is not enough to identify if the quark is in the confined or deconfined phase.

The running quark mass also shows a non-trivial dependence on the temperature of the heat bath. Indeed, the running quark mass is highly suppressed when T crosses $T_c$ from below, with typical values just above $T_c$ being about half of the corresponding values just below $T_c$. At low momenta $p \lesssim 1.5$ GeV for the temperatures considered here, the running quark mass is nearly constant above $T_c$. This can be viewed as favouring the description of quarks as free quasiparticles with a constant mass, as is used e.g. by the HTL approach. Our simulations also show that at high momenta the running quark mass reproduces the values of the bare quark mass reported in Table 1. For temperatures below $T_c$ the running quark mass increase when one approaches the zero momentum limit, reproducing the observed behaviour for the running quark mass at zero temperature.

Our simulations are based on pure gauge configurations, where the pure gauge sector is solved exactly but without taking into account the dynamics of quarks. The computed quark propagators refer to the propagation of the quark fields in a background of gluons that is solved exactly for the bosonic sector of the theory. The observed significant suppression of the running quark mass for temperatures above $T_c$, the critical temperature for gluon deconfinement, is an indication of a major contribution of the gluons for the mechanism of chiral symmetry breaking. Furthermore, our results suggest an important link between (gluon) confinement and the restoration of chiral symmetry that needs to be further investigated.

The continuum limit of the lattice computation for the quark propagator should be pursued to estimate the finite size effects in this propagator. The experience gained with the lattice computation of the gluon and ghost propagators at zero temperature, in the quenched approximation, suggests that the finite size effects are not a major problem.