1 Introduction

Supergravity is well motivated as the possible theoretical interface between (a) high-energy physics (well) beyond the Standard Model (SM) of elementary particles, (b) gravity beyond the Concordance (\(\Lambda \)CDM) Cosmological Model, and (c) string theory as the theory of quantum gravity whose low-energy effective action is described by supergravity. A phenomenological description of high energy particle physics and cosmology in supersymmetry (SUSY) and supergravity is known to be non-trivial, though many viable models exist, see e.g., the reviews [1,2,3,4] and the references therein. No signs of SUSY at the Large Hadron Collider (LHC) may hint towards a high scale of SUSY phenomena. At such scales (indirect) cosmological probes of SUSY prevail over (direct) experimental probes at particle colliders. The early Universe is, therefore, the natural place for physical applications of supergravity.

A simultaneous description of cosmological inflation and dark energy (as the positive cosmological constant) in supergravity is another challenge due to the huge difference in the relevant scales and the need of (spontaneous) SUSY breaking. The standard approach in supergravity is based on the use of chiral \(N=1\) superfields in four spacetime dimensions with the input given by a Kähler potential K and a superpotential W. Then the scalar potential and the kinetic terms of the scalar field components are uniquely defined, and the phenomenological model building amounts to choosing both K and W in order to achieve a viable single-field inflation consistent with the Cosmic Microwave Background (CMB) observations and a de Sitter (dS) vacuum after inflation. There are several problems with that approach. First, the input given by K and W allows infinitely many choices. Second, it always leads to the multi-scalar framework so that one has to choose the inflaton direction in the field space and suppress the non-inflaton scalars during inflation in order to prevent spoiling of the inflaton slow roll and get enough number of e-foldings. Third, after inflation one has to get the hierarchy between the (high) SUSY breaking scale allowing large masses for the superpartners of the SM particles and the (low) dark energy scale given by the cosmological constant. Getting that hierarchy may require two different mechanisms of spontaneous SUSY breaking.

It is possible to reduce (and minimize) the number of scalars in the inflationary models by employing a massive (irreducible) \(N=1\) vector multiplet as the inflaton supermultiplet, instead of a chiral one [5, 6]. The massive vector multiplet has only one (real) physical scalar that can be identified with inflaton, while its fermionic superpartner can be identified with goldstino in the minimalistic setup for inflation in supergraviity (cf. Refs. [7, 8]). To avoid SUSY restoration after inflation in a Minkowski vacuum (it was the drawback of the first supergravity models with inflaton in a vector multiplet), one may either add the hidden sector described by a chiral (Polonyi) superfield as in Refs. [9,10,11] or introduce the alternative (new) Fayet–Iliopoulos (FI) terms as in Refs. [12, 13].Footnote 1 Moreover, one can also combine both approaches and derive the supergravity-based inflationary models with inflaton in a massive vector multiplet in the presence of the FI term, with both F-type and D-type SUSY breaking needed for the hierarchy of scales [16, 17]. In all those cases, the canonical Kähler potential and a linear superpotential for Polonyi superfield were chosen, like the original Polonyi model [18].

Another approach is based on the use of the “dilaton–axion” superfield T by replacing the canonical (free) Kähler potential by the generalized “no-scale” one as follows [19]:

$$\begin{aligned} K=-\alpha \log (T+\overline{T}), \end{aligned}$$
(1)

The corresponding \(N=1\) non-linear sigma-model has the \(SL(2;\mathbb {R})/SO(2)\) (or \(SU(1,1;\mathbb {C})/U(1)\)) tangent space of Kähler curvature \(R_K=2/\alpha \), and is of particular interest for particle phenomenology because such Kähler potential in the case of \(\alpha =3\) arises in generic heterotic string compactifications and allows for the realistic particle model building [19,20,21,22]. Then T can be identified with the volume modulus of the compactified manifold in heterotic string theory. It is remarkable that the same Kähler potential with \(\alpha =3\) also arises in the modified F(R) supergravity after its dualization [23,24,25].

It is, however, also known that the case of \(\alpha =3\) in Eq. (1) with just a single chiral superfield is not viable for cosmological applications because it does not allow stable dS vacua and cannot be used for realizing Starobinsky inflation [26] with any choice of the superpotential W [3, 27,28,29,30], although there are single field models with generalized \(\alpha \) (\(\alpha \)-attractors) leading to a supersymmetric Minkowski vacuum [31,32,33].

The “no-scale” supergravity was successfully used for describing inflation in Refs. [27,28,29,30, 34, 35] with the help of at least two chiral superfields and the Kähler potential

$$\begin{aligned} K=-3\log \left( T+\overline{T}-\sum _{i=1}^{p-1} |\Phi ^i|^2/3\right) , \end{aligned}$$
(2)

where T is the volume modulus, and \(\Phi ^i\) are the matter chiral superfields parametrizing the non-linear sigma-model tangent space \(SU(p,1;\mathbb {C})/SU(p)\times U(1)\), with the suitable superpotential.

In this paper we use a single “dilaton–axion” chiral superfield T with the Kähler potential (1) but introduce a single vector multiplet in addition. We demonstrate that it leads to the viable set of cosmological models describing inflation, dS vacua and spontaneous SUSY breaking.

We recall that the original Starobinsky model of inflation [26] is based on the modified \((R+R^2)\) gravity, while its extension in the new-minimal formulation of supergravity has the dual description in terms of the standard supergravity coupled to a massive vector multiplet or, equivalently, a massless vector multiplet and a Stückelberg chiral multiplet with the Kähler potential [6]

$$\begin{aligned} K=-3\log (T+\overline{T})+3(T+\overline{T}). \end{aligned}$$
(3)

The last term can be identified with the FI term of the gauged R-symmetry (in a non-R-symmetric frame), because the D-term of this model results in the Starobinsky potential [5, 6, 36].

The authors of Ref. [37] studied even more general models of a single chiral multiplet and an abelian vector multiplet with the gauged R-symmetry and the Kähler potential having two parameters \(\alpha \) and \(\beta \),

$$\begin{aligned} K=-\alpha \log (T+\overline{T})+\beta (T+\overline{T}), \end{aligned}$$
(4)

and found that slow-roll inflation consistent with observations is only possible for \(\alpha =1,2\) after adding some non-perturbative corrections. SUSY is spontaneously broken after inflation in those models, with the gravitino mass in the TeV range.

In this paper we find that a non-vanishing D-term allows us to introduce the new inflationary models based on the Kähler potentials having the form (1) with a single chiral superfield and a single vector superfield. The other examples of the D-term based on the alternative FI terms [14, 15] can be found in Refs. [13, 38,39,40,41]. Those FI terms provide a tunable positive cosmological constant or dS uplifting of the vacuum after inflation [12, 16, 17, 42]. Our inflationary models in this paper have the Kähler potential (1) and the Polonyi-type linear superpotential (without gauging the shift symmetry of K) leading to the spontaneous F-type SUSY breaking. In addition, the simplest alternative FI term leads to another D-type SUSY breaking and uplifts an Anti-dS (AdS) minimum of the F-term scalar potential to a dS minimum.

The paper is organized as follows. Our setup is given in Sect. 2. In Sect. 3 we study vacua and SUSY breaking. In Sect. 4 we study inflation in our framework and analyze in detail the models with integer \(\alpha \). In particular, we derive the explicit values of the dilaton and axion masses and the SUSY breaking parameters by fixing the inflationary observables with the CMB observational data. We conclude in Sect. 5. The basic formulae about the standard \(N=1\) supergravity and the alternative FI term are given in Appendix. We set the reduced Planck mass as \(M_\mathrm{Pl}=\kappa ^{-1}=1\) unless otherwise stated.

2 The setup

Let us consider the following Kähler potential and the superpotential:

$$\begin{aligned} K= & {} -\alpha \log (T+\overline{T}), \end{aligned}$$
(5)
$$\begin{aligned} W= & {} \lambda +\mu T, \end{aligned}$$
(6)

where \(\alpha \) is a positive real constant, \(\lambda \) and \(\mu \) are complex parameters. The T is parametrized as

$$\begin{aligned} T=e^{-\sqrt{\frac{2}{\alpha }}\phi }+it \end{aligned}$$
(7)

in terms of the canonical inflaton \(\phi \) and its axionic partner t. The F-term scalar potential reads

$$\begin{aligned} V_F= & {} e^K\left[ K^{T\overline{T}}(W_T+K_TW)(\overline{W}_{\overline{T}} +K_{\overline{T}}\overline{W})-3|W|^2\right] \nonumber \\= & {} \frac{\alpha -3}{2^\alpha }(|\lambda |^2+\omega _2t+|\mu |^2t^2) e^{\sqrt{2\alpha }\phi }\nonumber \\&+\,\frac{(\alpha -5)\omega _1}{2^\alpha } e^{(\alpha -1)\sqrt{\frac{2}{\alpha }}\phi }\nonumber \\&+\,\frac{(\alpha ^2-7\alpha +4)| \mu |^2}{2^\alpha \alpha } e^{(\alpha -2)\sqrt{\frac{2}{\alpha }}\phi }, \end{aligned}$$
(8)

where we have used the parametrization (7) and the notation

$$\begin{aligned} \omega _1&\equiv \overline{\lambda }\mu +\lambda \overline{\mu } =2\lambda ^{}_R\mu ^{}_R+2\lambda ^{}_I\mu ^{}_I, \end{aligned}$$
(9)
$$\begin{aligned} \omega _2&\equiv i(\overline{\lambda }\mu -\lambda \overline{\mu }) =2\lambda ^{}_I\mu ^{}_R-2\lambda ^{}_R\mu ^{}_I. \end{aligned}$$
(10)

The subscripts R, I stand for the real and imaginary parts. It is convenient to trade the complex parameter \(\lambda \) for the two real ones, \(\omega _1\) and \(\omega _2\) defined above.

A generic vacuum of the F-term potential (8) is AdS. However, after introducing an abelian vector multiplet with the simplest alternative FI term [14, 15] and eliminating the auxiliary field (D) of the vector multiplet, one gets a positive contribution

$$\begin{aligned} V_D=\frac{g^2\xi ^2}{2} \end{aligned}$$
(11)

to the cosmological constant, where g is the gauge coupling, and \(\xi \) is the real FI constant.Footnote 2 More details about the alternative FI term and the bosonic action of the standard \(N=1\) supergravity can be found in Appendix.

3 Vacua and SUSY breaking

Let us analyze minima of the scalar potential (8). The vacuum equations for the critical points and the critical value \(V_0\) of the potential read

$$\begin{aligned} V_0&=Ax^\alpha +Bx^{\alpha -1}+Cx^{\alpha -2} +\frac{g^2\xi ^2}{2}, \end{aligned}$$
(12)
$$\begin{aligned} V_x&=\alpha Ax^{\alpha -1}+(\alpha -1)Bx^{\alpha -2} +(\alpha -2)Cx^{\alpha -3}=0, \end{aligned}$$
(13)
$$\begin{aligned} V_t&=\frac{\alpha -3}{2^\alpha } (\omega _2+2|\mu |^2t_0)x^\alpha =0, \end{aligned}$$
(14)

where we have used the notation

$$\begin{aligned} x&\equiv e^{\sqrt{\frac{2}{\alpha }}\phi _0}~~~\mathrm{with} ~~~\phi _0\equiv \langle \phi \rangle ,\nonumber \\ A&\equiv \frac{\alpha -3}{2^\alpha }(|\lambda |^2 +\omega _2t_0+|\mu |^2t_0^2),\nonumber \\ B&\equiv \frac{(\alpha -5)\omega _1}{2^\alpha }, ~~~C\equiv \frac{(\alpha ^2-7\alpha +4)|\mu |^2}{2^\alpha \alpha }, \end{aligned}$$
(15)

and \(V_x\equiv \partial V/\partial x\).

The special value \(\alpha =3\) yields the identically vanishing A and \(V_t\), thus making the potential t-independent. In the next Section we consider separately the case of \(\alpha =3\) and then turn to \(\alpha \ne 3\). When \(\alpha \ne 3\), we can use the solution to Eq. (14) as \(t_0=-\omega _2/(2|\mu |^2)\) and rewrite A as

$$\begin{aligned} A=\frac{\alpha -3}{2^\alpha } \left( |\lambda |^2-\frac{\omega _2^2}{4|\mu |^2}\right) =\frac{(\alpha -3)\omega _1^2}{2^{\alpha +2}|\mu |^2}, \end{aligned}$$
(16)

where in the last equation we have used the definitions (9) and (10). Since \(\omega _1\) is real, A becomes negative when \(\alpha <3\). Given negative A, the potential (12) is unbounded from below because A multiplies the highest power of x (for \(\alpha <3\) the potential also becomes unstable in the t-direction). Therefore, we restrict ourselves to \(\alpha \ge 3\) in what follows.

3.1 The case \(\alpha =3\)

Given \(\alpha =3\), the scalar potential takes the simple form

$$\begin{aligned} V=-\frac{\omega _1}{4}e^{\sqrt{\frac{8}{3}}\phi } -\frac{|\mu |^2}{3}e^{\sqrt{\frac{2}{3}}\phi }+\frac{g^2\xi ^2}{2}, \end{aligned}$$
(17)

and has a minimum at

$$\begin{aligned} \phi _0&=\sqrt{\frac{3}{2}}\log \left( -\frac{2|\mu |^2}{3\omega _1}\right) , \end{aligned}$$
(18)
$$\begin{aligned} V_0&=\frac{g^2\xi ^2}{2}+\frac{|\mu |^4}{9\omega _1}. \end{aligned}$$
(19)

The minimum exists only if \(\omega _1<0\). The minimum is AdS, Minkowski, or dS, depending on the following relations:

$$\begin{aligned} g^2\xi ^2&<\frac{2|\mu |^4}{9|\omega _1|} ~\longrightarrow ~\mathrm{AdS}, \end{aligned}$$
(20)
$$\begin{aligned} g^2\xi ^2&=\frac{2|\mu |^4}{9|\omega _1|} ~\longrightarrow ~\mathrm{Minkowski}, \end{aligned}$$
(21)
$$\begin{aligned} g^2\xi ^2&>\frac{2|\mu |^4}{9|\omega _1|} ~\longrightarrow ~\mathrm{dS}. \end{aligned}$$
(22)

Hence, by fine-tuning the parameters we can obtain a small positive cosmological constant \(V_0\) for the realistic phenomenology.

Defining \(\varphi \equiv \phi -\phi _0\) as excitation of the inflaton around its Vacuum Expectation Value (VEV), the potential (17) can be brought to the form [after using Eq. (19) to eliminate \(g\xi \) in terms of \(V_0\)]

$$\begin{aligned} V=V_0+\frac{|\mu |^4}{9|\omega _1|} \left( e^{\sqrt{\frac{2}{3}}\varphi }-1\right) ^2 \end{aligned}$$
(23)

that gives the realization of the Starobinsky inflationary model (with the cosmological constant) in our framework. The potential is t-flat.

SUSY is spontaneously broken by the constant non-vanishing D-term, \(D=\langle D \rangle =g\xi \), while \(\langle F_T\rangle \) and the gravitino mass are given by

$$\begin{aligned} \langle F_T\rangle&=\langle -e^{K/2}K^{T\overline{T}} (\overline{W}_{\overline{T}}+K_{\overline{T}}\overline{W})\rangle \nonumber \\&=-\frac{i~\mathrm{sgn}(\mu )}{\sqrt{12|\omega _1|}}(\omega _2+2|\mu |^2t_0), \end{aligned}$$
(24)
$$\begin{aligned} m_{3/2}^2&=\langle e^K|W|^2\rangle =|-2\omega _1+i(\omega _2+2|\mu |^2t_0)|^2 \frac{|\mu |^4}{108|\omega _1|^3}. \end{aligned}$$
(25)

Though \(\langle F_T\rangle \) is arbitrary (and may even vanish), the gravitino mass is bounded from below,

$$\begin{aligned} m_{3/2}^2\ge \frac{|\mu |^4}{27|\omega _1|}. \end{aligned}$$
(26)

The mass of the inflaton is

$$\begin{aligned} m^2_{\varphi }=\frac{4|\mu |^4}{27|\omega _1|}, \end{aligned}$$
(27)

so that we have the relation \(2m_{3/2}\ge m_{\varphi }\).

The bosonic sector also includes a massless axion t and a massless vector. The vector can be made massive via (additional) super-Higgs effect. A massless scalar is phenomenologically problematic, but the mass of t may be generated either by quantum corrections when \(\alpha =3\) (as is usually assumed in the “no-scale” supergravity models), or already at the tree level when \(\alpha >3\), as we are going to show in the next Subsection.

3.2 The case \(\alpha >3\): vacuum solutions

If the axion field is fixed at its VEV, \(t_0=-\omega _2/(2|\mu |^2)\), we can rewrite the scalar potential (8) and (2) for \(\alpha >3\) as

$$\begin{aligned} V= & {} \frac{(\alpha -3)\omega _1^2}{2^{\alpha +2}|\mu |^2} e^{\sqrt{2\alpha }\phi }+\frac{(\alpha -5)\omega _1}{2^\alpha } e^{(\alpha -1)\sqrt{\frac{2}{\alpha }}\phi }\nonumber \\&+\,\frac{(\alpha ^2-7\alpha +4)|\mu |^2}{2^\alpha \alpha } e^{(\alpha -2)\sqrt{\frac{2}{\alpha }}\phi }+\frac{1}{2}g^2\xi ^2, \end{aligned}$$
(28)

assuming \(\omega _1\ne 0\). The vacuum equations (12) and (13) then take the form

$$\begin{aligned} V_0= & {} \frac{(\alpha -3)\omega _1^2}{2^{\alpha +2}|\mu |^2}x^\alpha +\frac{(\alpha -5)\omega _1}{2^\alpha }x^{\alpha -1}\nonumber \\&+\,\frac{(\alpha ^2-7\alpha +4)|\mu |^2}{2^\alpha \alpha }x^{\alpha -2} +\frac{1}{2}g^2\xi ^2, \end{aligned}$$
(29)
$$\begin{aligned} V_x= & {} \frac{\alpha (\alpha -3)\omega _1^2}{2^{\alpha +2}|\mu |^2}x^{\alpha -1} +\frac{(\alpha -1)(\alpha -5)\omega _1}{2^\alpha }x^{\alpha -2}\nonumber \\&+\,\frac{(\alpha -2)(\alpha ^2-7\alpha +4)|\mu |^2}{2^\alpha \alpha } x^{\alpha -3}=0, \end{aligned}$$
(30)

where \(x\equiv e^{\phi _0/\sqrt{2}}\) as before. Equation (30) has two solutions,

$$\begin{aligned} x_+=\frac{2(-\alpha ^2+7\alpha -4)|\mu |^2}{\alpha (\alpha -3)\omega _1}, ~~~x_-=\frac{2(2-\alpha )|\mu |^2}{\alpha \omega _1}, \end{aligned}$$
(31)

that we parametrize as

$$\begin{aligned} x_{\pm }=\gamma _{\pm }\frac{|\mu |^2}{\omega _1}~~{\left\{ \begin{array}{ll} \gamma _+\equiv \frac{2(-\alpha ^2+7\alpha -4)}{\alpha (\alpha -3)},\\ \gamma _-\equiv \frac{2(2-\alpha )}{\alpha }. \end{array}\right. } \end{aligned}$$
(32)

The positivity of x requires \(\gamma /\omega _1\) to be positive. Since we have \(\alpha >3\), the \(\gamma _-\) is always negative, while the sign of \(\gamma _+\) depends on the choice of \(\alpha \). More specifically, we findFootnote 3

$$\begin{aligned} 3<\alpha <\frac{1}{2}(7+\sqrt{33})~\longrightarrow ~\gamma _+>0. \end{aligned}$$
(33)

Hence, if \(\omega _1>0\), the \(x_+\) should be used as the vacuum solution in this parameter region. On the other hand,

$$\begin{aligned} \alpha =\frac{1}{2}(7+\sqrt{33})~\longrightarrow ~\gamma _+=0, \end{aligned}$$
(34)

that invalidates the \(x_+\) as a stable solution for the given value of \(\alpha \). Thus \(\omega _1\) must be negative and \(x_-\) should be used as the minimum. Moreover,

$$\begin{aligned} \alpha >\frac{1}{2}(7+\sqrt{33})~\longrightarrow ~\gamma _+<0. \end{aligned}$$
(35)

This means that \(\omega _1\) should be negative. In this case, both \(x_+\) and \(x_-\) (i.e. \(\phi _+\) and \(\phi _-\)) are the valid stationary points and, in fact, the extrema – not inflection points – because

$$\begin{aligned} \left. \frac{\partial ^2 V(\phi )}{\partial \phi ^2}\right| _{\phi =\phi _{\pm }}\ne 0, \end{aligned}$$
(36)

where \(V(\phi )\) is given by Eq. (28). Setting \(\xi =0\) and using \(\omega _1=-|\omega _1|\), we get

$$\begin{aligned} V_0|_{\phi =\phi _+}&=\frac{|\mu |^{2(\alpha -1)}}{2^{\alpha +2} \alpha |\omega _1|^{\alpha -2}}\left( \frac{\alpha ^2-7\alpha +4}{\alpha (\alpha -3)}\right) ^{\alpha -1}>0, \end{aligned}$$
(37)
$$\begin{aligned} V_0|_{\phi =\phi _-}&=-\frac{3|\mu |^{2(\alpha -1)}}{2^{\alpha +2}|\omega _1|^{\alpha -2}} \left( \frac{1-\frac{2}{\alpha }}{(\alpha -2)^2}\right) <0, \end{aligned}$$
(38)

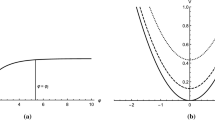
for \(\alpha >(7+\sqrt{33})/2\). It means that \(\phi _+\) is a local maximum, while \(\phi _-\) is a global minimum. The general form of the potential is shown in Fig. 1. The existence of the local maximum at \(\phi _+\) means that the potential is of the hilltop-type and, therefore, we should consider inflation in the cases \(3\le \alpha \le (7+\sqrt{33})/2\) and \(\alpha >(7+\sqrt{33})/2\) separately. Since the value of \(\alpha =(7+\sqrt{33})/2\) is special, we introduce the notation

$$\begin{aligned} \alpha _*\equiv \frac{1}{2}(7+\sqrt{33})\approx 6.37. \end{aligned}$$
(39)

It is noteworthy that the choice of \(\alpha =5\) leads to \(\gamma _+=-\gamma _-=6/5\), so that the scalar potentials in the cases \(\omega _1>0\) and \(\omega _1<0\) exactly coincide.

Fig. 1
figure 1

The form of the scalar potential (28) for \(\alpha >\frac{1}{2}(7+\sqrt{33})\), \(\xi =0\), and negative \(\omega _1\). The \(\phi _{\pm }\) are defined as \(x_{\pm }=e^{\phi _{\pm }/ \sqrt{2}}\), where \(\phi _-=\phi _0\) is the VEV of \(\phi \)

Full size image
Fig. 2
figure 2

The mass ratios \(\Delta _\pm \) and \(\Gamma _\pm \) evaluated at \(3<\alpha <\alpha _*\approx 6.37\). In the plot (a) the dashed lines denote the points on the \(\alpha \)-axis where \(\Delta _+=1\) and \(\Gamma _+=1\), whose values are (from the left to the right) approximately 3.8, 5.27, and 5.37

Full size image

3.3 The case \(\alpha >3\): SUSY breaking and scalar masses

In the case of \(3<\alpha \le \alpha _*\) we use again the axion VEV, \(t_0=-\omega _2/(2|\mu |^2)\), and the general solution \(x=\gamma |\mu |^2/\omega _1\) to find \(F_T\) and the gravitino mass at the minimum,

$$\begin{aligned} \langle F_T\rangle&=\frac{(\gamma \alpha +2\alpha -4)| \mu |^{2-\alpha }}{2^{\alpha /2}\alpha \mu } \left( \frac{\gamma }{\omega _1}\right) ^{\frac{\alpha }{2}-2}, \end{aligned}$$
(40)
$$\begin{aligned} m^2_{3/2}&=\frac{(\gamma +2)^2|\mu |^{2(\alpha -1)}}{4\cdot 2^\alpha } \left( \frac{\gamma }{\omega _1}\right) ^{\alpha -2}. \end{aligned}$$
(41)

Substituting the two solutions from Eq. (32) yields

$$\begin{aligned} \langle F_T\rangle |_{x_+}&=\frac{(\alpha +1)|\mu |^{\alpha -2}}{\alpha ^{\frac{\alpha }{2}-1} (\alpha -3)\mu }\left[ \frac{\alpha ^2-7\alpha +4}{(3-\alpha ) \omega _1}\right] ^{\frac{\alpha }{2}-2}, \end{aligned}$$
(42)
$$\begin{aligned} \langle F_T\rangle |_{x_-}&=0, \end{aligned}$$
(43)

while the gravitino mass in both cases (\(x_+\) and \(x_-\)) is non-vanishing. Now recall that for \(3<\alpha <\alpha _*\) the vacuum solution is \(x_+\) if \(\omega _1\) is positive, and \(x_-\) if \(\omega _1\) is negative, while for \(\alpha \ge \alpha _*\) only \(x_-\) can be a stable vacuum solution and this requires a negative \(\omega _1\). Thus, we conclude that if \(3<\alpha <\alpha _*\), a positive \(\omega _1\) leads to the mixed F- and D-term SUSY breaking, while a negative \(\omega _1\) leads to the pure D-term SUSY breaking. If \(\alpha \ge \alpha _*\), only the pure D-term breaking is possible (we exclude runaway solutions).

As for the mass of the axion t, we first get

$$\begin{aligned} m_t^2=\frac{(\alpha -3)|\mu |^2}{2^{\alpha -1}}e^{\sqrt{2\alpha }\phi _0}. \end{aligned}$$
(44)

However, the t is not canonical at the \(\phi \)-minimum because the \(\phi _0\) is non-vanishing and

$$\begin{aligned} e^{-1}{\mathcal {L}}_\mathrm{kin}(t,\phi _0)=-\frac{\alpha }{4} e^{\sqrt{\frac{8}{\alpha }}\phi _0}(\partial t)^2, \end{aligned}$$
(45)

as can be seen from Eq. (71) in Appendix. Though it is impossible to canonically normalize the kinetic term of t for all values of \(\phi \), it is certainly possible at the reference point \(\phi _0\) by the rescaling

$$\begin{aligned} t=\sqrt{\frac{2}{\alpha }}e^{-\sqrt{\frac{2}{\alpha }}\phi _0}t', \end{aligned}$$
(46)

where \(t'\) is the “canonical” axion. Its mass squared is then given by

$$\begin{aligned} m_{t'}^2= & {} \frac{(\alpha -3)|\mu |^2}{2^{\alpha -2}\alpha } e^{(\alpha -2)\sqrt{\frac{2}{\alpha }}\phi _0}\nonumber \\= & {} \frac{(\alpha -3)|\mu |^{2(\alpha -1)}}{2^{\alpha -2}\alpha } \left( \frac{\gamma }{\omega _1}\right) ^{\alpha -2}, \end{aligned}$$
(47)

where we have used the general vacuum solution \(e^{\sqrt{\frac{2}{\alpha }}\phi _0}\equiv x=\gamma |\mu |^2/\omega _1\).

The inflaton mass can be read off from Eq. (28) after using \(\varphi =\phi -\phi _0\) and substituting the general x solution (32). We find

$$\begin{aligned} m_\varphi ^2= & {} 2\left( \frac{\gamma }{2}\right) ^\alpha \nonumber \\&\times \, \left[ \frac{\alpha (\alpha -3)}{4}+\frac{(\alpha -5) (\alpha -1)^2}{\alpha \gamma }\right. \nonumber \\&\left. +\,\frac{(\alpha ^2-7\alpha +4) (\alpha -2)^2}{\alpha ^2\gamma ^2}\right] \frac{|\mu |^{2(\alpha -1)}}{\omega _1^{\alpha -2}}. \end{aligned}$$
(48)

It is convenient to define the mass ratios

$$\begin{aligned} \Delta _\pm \equiv \left. \frac{m_{t'}}{m_\varphi }\right| _{\gamma =\gamma _\pm }, ~~~\Gamma _\pm \equiv \left. \frac{m_{3/2}}{m_\varphi }\right| _{\gamma =\gamma _\pm }, \end{aligned}$$
(49)

where the \(\gamma _{\pm }\) are defined in Eq. (32). The parameters \(\mu \) and \(\omega _1\) cancel out in \(\Delta \) and \(\Gamma \) that can be readily plotted as the functions of \(\alpha \).

In Fig. 2 we plot the mass ratios for \(3<\alpha <\alpha _*\). Figure 2a shows that with \(\gamma _+\) corresponding to a positive \(\omega _1\) axion is lighter than inflaton if \(\alpha <(5+\sqrt{33})/2\approx 5.37\), whereas beyond this point axion becomes heavier. Gravitino (with \(\gamma _+\)) is slightly lighter than inflaton in the range \(3.8\lessapprox \alpha \lessapprox 5.27\), whereas outside this range gravitino becomes heavier.Footnote 4

In the case of \(\gamma _-\) (see Fig. 2b), i.e. a negative \(\omega _1\), both axion and gravitino are lighter than inflaton. As we already showed, \(x_-\) is the global minimum of the potential even when \(\alpha >\alpha _*\), so that the mass ratios \(\Delta _-\) and \(\Gamma _-\) can be extrapolated for large values of \(\alpha \) as

$$\begin{aligned} \lim _{\alpha \rightarrow \infty }\Delta _-=1, ~~~\lim _{\alpha \rightarrow \infty }\Gamma _-=0, \end{aligned}$$
(50)

i.e. the axion mass approaches the inflaton mass, while the gravitino mass slowly vanishes for large \(\alpha \).

4 Inflation

In order to study inflation, let us restore the gravitational constant \(\kappa \equiv \sqrt{8\pi G}=M_P^{-1}\). We choose the Kähler potential and the chiral field T to be dimensionless, whereas the superpotential has the mass dimension three, \([W]=M^3\). It follows that \([\lambda ]=[\mu ]=M^3\) and \([\omega _1]=M^6\), where \([\ldots ]\) stands for the mass dimension of the corresponding quantity. We also set \([g\xi ]=M^0\) and \([\phi ]=[\varphi ]=M\).

It is convenient to express the FI constant \(g\xi \) in terms of the cosmological constant \(V_0\) by using Eq. (29) and the general x-solution (32). Restoring \(\kappa \) results in the potential

$$\begin{aligned} V= & {} V_0+\kappa ^2\left( \frac{\gamma }{2}\right) ^\alpha \frac{|\mu |^{2(\alpha -1)}}{\omega _1^{\alpha -2}}\nonumber \\&\times \left[ \frac{\alpha -3}{4}e^{\sqrt{2\alpha }\kappa \varphi } +\frac{\alpha -5}{\gamma }e^{(\alpha -1) \sqrt{\frac{2}{\alpha }}\kappa \varphi }\right. \nonumber \\&+ \frac{\alpha ^2-7\alpha +4}{\alpha \gamma ^2}e^{(\alpha -2) \sqrt{\frac{2}{\alpha }}\kappa \varphi }\nonumber \\&\left. - \frac{\alpha (\gamma +2)^2}{4\gamma ^2} +\frac{(\gamma +2)(3\gamma +14)}{4\gamma ^2} -\frac{4}{\alpha \gamma ^2}\right] . \end{aligned}$$
(51)

In what follows we neglect the cosmological constant \(V_0\).

We use the standard definitions of the slow-roll parameters,

$$\begin{aligned} \epsilon \equiv \frac{1}{2\kappa ^2} \left( \frac{V'(\varphi )}{V(\varphi )}\right) ^2, ~~~\eta \equiv \frac{1}{\kappa ^2}\frac{V''(\varphi )}{V(\varphi )}. \end{aligned}$$
(52)

Inflation ends when \(\epsilon =1\) that translates into the value of the inflaton field at the end of inflation, \(\varphi _f\). The scalar spectral index and the tensor-to-scalar ratio are related to the slow-roll parameters as

$$\begin{aligned} n_s=1+2\eta _i-6\epsilon _i,~~~r=16\epsilon _i, \end{aligned}$$
(53)

respectively. Here the subscript i means evaluation at the initial value of the inflaton, \(\varphi _i\) i.e., at the horizon crossing. The number of e-foldings between \(\varphi _i\) and \(\varphi _f\) is given by

$$\begin{aligned} N_e=\kappa ^2\int ^{\varphi _i}_{\varphi _f}d\varphi \frac{V}{V'}. \end{aligned}$$
(54)

Another important observable is the amplitude of scalar perturbations given by

$$\begin{aligned} A_s=\frac{\kappa ^4V(\varphi _i)}{24\pi ^2\epsilon _i}. \end{aligned}$$
(55)
Fig. 3
figure 3

The tilt \(n_s\) as a function of \(\alpha \) for positive and negative \(\omega _1\), and \(50\le N_e\le 60\). The values \(n_s=0.9691\) and \(n_s=0.9607\) are the upper and lower observational limits (\(68\%\hbox {CL}\)), respectively

Full size image

According to the PLANCK data (2018), the observed values of \(n_s\), r, and \(A_s\) are [44]

$$\begin{aligned}&n_s=0.9649\pm 0.0042~\mathrm{(68\% CL)},~~~r<0.064~\mathrm{(95\%CL)}, \end{aligned}$$
(56)
$$\begin{aligned}&\log (10^{10}A_s)=2.975\pm 0.056~\mathrm{(68\% CL)}\nonumber \\&\quad ~\Rightarrow ~A_s \approx 1.96\times 10^{-9}. \end{aligned}$$
(57)

In our models, \(n_s\) and r depend only on \(\alpha \) and \(\mathrm{sgn}(\omega _1)\) (and not on the value of \(\omega _1\)) which determine the shape of the scalar potential. The observed value of \(A_s\) (\(\sim 10^{-9}\)) can be used to fix the composite parameter \(|\mu |^{2(\alpha -1)}/\omega _1^{\alpha -2}\) that is related to the inflaton mass via Eq. (48).

First, we numerically evaluate \(n_s\) as a function of \(\alpha \) for \(N_e=50\) to 60. The results of the evaluation are presented in Fig. 3. Figure 3a shows the tilt \(n_s(\alpha )\) evaluated for a positive \(\omega _1\) and \(3<\alpha <\alpha _*\), while Fig. 3b shows the tilt \(n_s(\alpha )\) evaluated for a negative \(\omega _1\) and \(3\le \alpha \le 7.6\). The \(\omega _1>0\) case, in part due to its limited domain of validity (\(3<\alpha <\alpha _*\)), is fully compatible with the observations of the spectral tilt \(n_s\). However, in the \(\omega _1<0\) case, if \(\alpha \) is greater than the certain value around 7.2 (let us call this value \(\alpha _\mathrm{max}\)), the predicted value of \(n_s\) becomes smaller than the lower observational limit \(n_s=0.9607\).Footnote 5 A more precise value of \(\alpha _\mathrm{max}\) can be derived by finding \(\varphi _i\) that solves the condition \(n_s(\varphi _i)=0.9607\) and substituting this value in Eq. (54) to solve \(N_e(\alpha )=60\). This results in

$$\begin{aligned} \alpha _\mathrm{max}\approx 7.235. \end{aligned}$$
(58)

Therefore, when \(\omega _1<0\) we exclude the models with \(\alpha >\alpha _\mathrm{max}\).

As we show below, the tensor-to-scalar ratio r decreases with increasing \(\alpha \) and is always compatible with the limit \(r<0.064\).

4.1 The case \(3\le \alpha \le \alpha _*\): starobinsky-like inflation

Let us divide our models into two classes for \(3\le \alpha \le \alpha _*\) and \(\alpha _*<\alpha \le \alpha _\mathrm{max}\), respectively. The reason is that in the range \(3\le \alpha \le \alpha _*\) the inflationary potential is truly Starobinsky-like and has a single extremum, namely, the global minimum and the infinite plateau asymptotically approaching a constant positive height. In contrast, if \(\alpha >\alpha _*\) the potential has a local maximum, which means that we get the hilltop inflationary models.

For simplicity, we restrict ourselves to integer \(\alpha \), and proceed with calculating the inflationary parameters \(n_s\) and r for \(3\le \alpha \le \alpha _*\) by setting \(N_e=55\). In this subsection, we take \(\alpha =3,4,5,6\) (\(\alpha =3\) is the Starobinsky case) and, in addition, we include the upper limit \(\alpha =\alpha _* \equiv (7+\sqrt{33})/2\). The results of our numerical calculations of \(n_s\) and r are in Table 1, and the corresponding scalar potentials for the chosen values of \(\alpha \) are in Fig. 4.

Table 1 The predictions for the inflationary parameters (\(n_s\), r), and the values of \(\varphi \) at the horizon crossing (\(\varphi _i\)) and at the end of inflation (\(\varphi _f\)), in the case \(3\le \alpha \le \alpha _*\) with both signs of \(\omega _1\). The \(\alpha \) parameter is taken to be integer, except of the upper limit \(\alpha _*\equiv (7+\sqrt{33})/2\)
Full size table
Fig. 4
figure 4

The scalar potentials for both signs of \(\omega _1\) and the integer values of \(\alpha \) in the range \(3\le \alpha \le \alpha _*\). The inflaton mass (see Eq. 48) and \(\kappa \) are set to be one

Full size image

The relation to the amplitude \(A_s\) of CMB scalar perturbations in Eq. (55) is conveniently described by the composite parameter

$$\begin{aligned} \Lambda ^6\equiv \frac{|\mu |^{2(\alpha -1)}}{|\omega _1|^{\alpha -2}}, \end{aligned}$$
(59)

where \(\Lambda \) has units of mass. When \(\omega _1<0\) and \(3\le \alpha \le \alpha _*\), Eq. (57) yields \(\Lambda \sim 10^{101/6}~\mathrm{GeV}\sim 10^{16.8}~\mathrm{GeV}\), whereas in the case of \(\omega _1>0\) and \(3<\alpha <\alpha _*\) we find

$$\begin{aligned} \lim _{\alpha \rightarrow 3}\Lambda =0, ~~~\lim _{\alpha \rightarrow \alpha _*}\Lambda =\infty , \end{aligned}$$
(60)

due to the behavior of \(\gamma _+(\alpha )\) (see Eq. 32) in the scalar potential (51). Given \(\alpha =4,5,6\), the parameter \(\Lambda \) is of the order \(10^{16.5},10^{16.8}, 10^{17.5}~\mathrm{GeV}\), respectively.

The inflaton mass is \(m_\varphi \sim 10^{13}~\mathrm{GeV}\) irrespectively of the choice of \(\alpha \) and \(\mathrm{sgn}(\omega _1)\).

4.2 The case \(\alpha >\alpha _*\): hilltop inflation

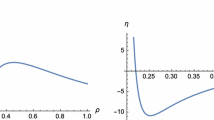
The viable hilltop inflationary models are limited to \(\alpha _*< \alpha \le \alpha _\mathrm{max}\) with \(\alpha _*=(7+\sqrt{33})/2\approx 6.372\) and \(\alpha _\mathrm{max}\approx 7.235\). Let us consider \(\alpha =7\), because it is the only integer between \(\alpha _*\) and \(\alpha _\mathrm{max}\).

Taking \(N_e=60\) (for a better fit of \(n_s\) with PLANCK data), we calculate the parameters as follows: \(n_s\approx 0.9635\), \(r\approx 0.0002\), and \(\Lambda \sim 10^{16.8}~\mathrm{GeV}\). The form of the scalar potential is given in Fig. 5 where the local maximum \(\varphi _+\) and the starting point of inflation \(\varphi _i\) are shown.

Fig. 5
figure 5

The scalar potential (51) for \(\alpha =7\), \(\omega _1<0\), and thus \(\gamma =\gamma _-\) (\(m_\varphi =\kappa =1\)). The solid vertical line shows the local maximum \(\varphi _+\), and the dashed vertical line shows the starting point of inflation \(\varphi _i\) when \(N_e=60\)

Full size image

4.3 SUSY breaking scale

Let us parametrize the SUSY breaking scale by the gravitino mass that can be read off from Fig. 2 after taking into account the inflaton mass fixed by the observed value of \(A_s\) in Eq. (57). For example, if \(\omega _1>0\), \(m_{3/2}\) ranges from the inflationary scale to arbitrarily high scale (as \(\alpha \rightarrow 3\) or \(\alpha \rightarrow \alpha _*\)). If \(\omega _1<0\) and \(3\le \alpha \le \alpha _\mathrm{max}\), the gravitino mass is always lower than \(m_\varphi \) by at most one order of the magnitude. The exception is the value \(\alpha =3\) when \(m_{3/2}\ge m_\varphi /2\) as is shown in Eq. (26).

Table 2 The masses of inflaton, axion and gravitino, and the VEVs of F- and D-fields derived from our models by fixing the amplitude \(A_s\) according to PLANCK data – see Eq. (57). The value of \(\langle F_T\rangle \) for a positive \(\omega _1\) is not fixed by \(A_s\)
Full size table

In Table 2 we provide the explicit values of \(m_\varphi \), \(m_{t'}\), \(m_{3/2}\), \(\langle F_T\rangle \), and \(\langle D\rangle \) for the integer values of \(\alpha \) between 3 and \(\alpha _\mathrm{max}\approx 7.235\), derived from our models by fixing \(A_s\) according to Eq. (57). This fixes \(\langle D\rangle =\kappa ^{-2}g\xi \) [by using Eqs. (29) and (32)], but it is not enough to fix \(\langle F_T\rangle \) in the \(\omega _1>0\) case (when \(\omega _1<0\), the \(\langle F_T\rangle \) identically vanishes except for \(\alpha =3\) where it is undetermined). In particular, for \(\alpha =4,5,6\), Eq. (42) yields

$$\begin{aligned} \langle F_T\rangle =\frac{5}{4}\overline{\mu }\kappa ,~~\langle F_T\rangle =\sqrt{\frac{3}{5}}^{3}\frac{\overline{\mu }|\mu |}{\sqrt{\omega _1}}\kappa , ~~~\langle F_T\rangle =\frac{7\overline{\mu }|\mu |^2}{162\omega _1}\kappa , \end{aligned}$$
(61)

respectively. There is always enough freedom to choose the values of \(\langle F_T\rangle \) independently of the parameter \(\Lambda ^6 =|\mu |^{2(\alpha -1)}/|\omega _1|^{\alpha -2}\) that is fixed by the observed amplitude \(A_s\).

The most important prediction of our models (apart from the existence of the upper limit \(\alpha _\mathrm{max}\)) for integer \(\alpha \) is the very high SUSY breaking scale parametrized by the superheavy gravitino mass \(m_{3/2}\) of the order of \(10^{12}\) to \(10^{13}\ \hbox {GeV}\). For fractional \(\alpha \), if \(\omega _1>0\), the SUSY breaking scale can be arbitrarily high as \(\alpha \) approaches 3 or \(\alpha _*\).

5 Conclusion

In this paper we studied a class of unified models of inflation, spontaneous SUSY breaking, and dark energy (described by the positive cosmological constant) based on the generalized dilaton–axion multiplet coupled to \(N=1\) supergravity with the Kähler potential and superpotential

$$\begin{aligned} K=-\alpha \log (T+\overline{T}),~~~W=\lambda +\mu T, \end{aligned}$$
(62)

in the presence of a single vector multiplet with the gauge kinetic function \(f=1\). In order to uplift the resulting AdS vacuum, we used the alternative FI term introduced in Refs. [14, 15]. This allowed us to get a tunable positive cosmological constant and the D-term contribution to SUSY breaking.

We showed that, unless \(\alpha \ge 3\), the scalar potential is unstable. The choice \(\alpha =3\) leads to the Starobinsky potential for the dilaton \(\varphi \), while the axion direction is flat, i.e. the axion mass has to be generated by quantum corrections. On the other hand, for \(\alpha >3\) the axion has a positive non-vanishing mass squared and is automatically stabilized. Once the axion acquires a VEV, those models lead to the effective single-field inflation where inflaton is identified with dilaton. We found that the shape of the potential, and thus the inflationary observables \(n_s\) and r, are controlled by \(\alpha \) and the sign of the real parameter \(\omega _1\equiv \overline{\lambda }\mu +\lambda \overline{\mu }\), whereas the amplitude of scalar perturbations is related to the value of the composite parameter \(\Lambda ^6=|\mu |^{2(\alpha -1)}/ |\omega _1|^{\alpha -2}\). In particular, when \(3\le \alpha \le \alpha _*\) (\(\alpha _*\approx 6.372\)), the derived inflation is of the Starobinsky type where the inflaton rolls down an infinite plateau, while for \(\alpha >\alpha _*\) the potential has a local maximum (hilltop).

One of our main results is the upper limit on \(\alpha \): by analyzing the dependence of \(n_s\) on \(\alpha \) (Fig. 3), we found that \(\alpha _\mathrm{max}\approx 7.235\) is the maximum value that can reproduce the observed spectral tilt \(n_s=0.9649\pm 0.0042\). More precise observations of \(n_s\) may further reduce the value of \(\alpha _\mathrm{max}\).

Another important prediction of our models is the (very) high-scale SUSY breaking, so that for integer \(\alpha \) the gravitino mass is roughly of the order of the inflaton mass, \(m_{3/2}\sim m_\varphi \sim 10^{13}\ \hbox {GeV}\) (for fractional \(\alpha \), \(m_{3/2}\) can be arbitrarily high). In comparison, the scale of the D-term is \(\sqrt{|\langle D\rangle |}=\kappa ^{-1}\sqrt{g|\xi |}\sim 10^{15.5}\ \hbox {GeV}\). We explicitly derived the masses of dilaton, axion and gravitino, together with the SUSY breaking parameters \(\langle F_T\rangle \) and \(\langle D\rangle \) for \(\alpha =3,4,5,6,7\) (see Table 2). It is interesting that the models with a negative \(\omega _1\) have the vanishing F-terms \(\langle F_T\rangle =0\) (except for \(\alpha =3\)), so that SUSY is broken purely by the D-term. Those models may be interesting in connection to the universality of scalar masses in the Supersymmetric Standard Model due to the vanishing F-terms, see e.g., Refs. [45, 46], though more research is needed in this direction. The axions and gravitinos in our models can be used as the superheavy dark matter along the lines of Refs. [11, 47,48,49,50,51].

Although the origin of the alternative FI terms in superstring theory is not clear, the generalized dilaton–axion superfield with the Kähler potential given by Eq. (62) with \(\alpha =1,2,\ldots ,7\) may be derived from M-theory compactified on a \(G_2\) manifold [52,53,54], where the effective \(N=1\), \(D=4\) supergravity has seven complex scalars parametrizing the \(SL(2;\mathbb {R})^7/SO(2)^7\) manifold with the Kähler potential

$$\begin{aligned} K=-\sum _{i=1}^7\log (\Phi _i+\overline{\Phi }_i). \end{aligned}$$
(63)

Then various integer values of \(\alpha \) can be obtained by selecting a desired number of \(\Phi _i\) superfields and setting the others to be constants. For example, in order to obtain \(\alpha =5\), we can choose \(\Phi _1=\Phi _2=\cdots =\Phi _5\) and \(\Phi _6=\Phi _7=\mathrm{const}\).