Abstract
In this paper, we analyze deflection angle of photon from magnetized black hole within non-linear electrodynamics with parameter \(\beta \). In doing so, we find the corresponding optical spacetime metric and then we calculate the Gaussian optical curvature. Using the Gauss–Bonnet theorem, we obtain the deflection angle of photon from magnetized black hole in weak field limits and show the effect of non-linear electrodynamics on weak gravitational lensing. We also analyzed that our results reduces into Maxwell’s electrodynamics and Reissner–Nordström (RN) solution with the reduction of parameters. Moreover, we also investigate the graphical behavior of deflection angle w.r.t correction parameter, black hole charge and impact parameter.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In 1916, Einstein cleverly predicted the existence of gravitational waves and gravitational lensing as part of the theory of general relativity [1]. In 2015, the gravitational waves were detected by LIGO [2], which shows that the theoretical predictions are well fitted with experimental observations. Hence, this new detection of gravitational waves marks not only a culmination of a decades-long search, but also the beginning of a new way to look at the universe. After detection of gravitational waves by LIGO, there is renewed interest in the topic of gravitational lensing [3]. Gravitational lensing first proposed by Soldner in 1801 in context of Newtonian theory [4]. Many useful results for cosmology have come out of using this property of matter and light. Then using data taken during a solar eclipse in 1919, Eddington measured a value close to that of the GR prediction [5, 6]. Then gravitational lensing has been worked in various space-times using different methods [7,8,9,10,11,12,13,14,15].
Moreover, over the years, there have been many studies linking gravitational lensing with the Gauss–Bonnet theorem (GBT) after Gibbons and Werner (GW) elegantly showed that the possible way of calculation the deflection angle using the GBT for asymptotically flat static black holes [16]:
Here \({\mathcal {K}}\) and \(\mathrm {d}\sigma \) are the Gaussian curvature and surface element of optical metric.
Afterwards, Werner extended this method for stationary black holes [17]. Next, Ishihara et al. [18] showed that it is possible to find deflection angle for the finite-distances (large impact parameter) because the GW only found the deflection angle using the optical Fermat geometry of the black hole’s spacetime in weak field limits and for the observers at asymptotically flat region. Recently, Crisnejo and Gallo have studied the deflection of light in a plasma medium [19]. Since then, there is a continuously growing interest to the weak gravitational lensing via the method of GW and GBT of black holes, wormholes or cosmic strings [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40].
The main aim of this paper is to investigate the effect of the nonlinear electrodynamics (magnetized) charge on the deflection angle where we use the GBT in which the deflection of light become a global effect [41]. Because we only focus the nonsingular region outside of a photon rays.
Gravitational singularities are mainly considered within general relativity, where density apparently becomes infinite at the center of a black hole, and within astrophysics and cosmology as the earliest state of the universe during the Big Bang. In general theory of gravity, spacetime singularities raise a number of problems, both mathematical and physical [42,43,44,45,46,47,48,49,50]. Using the nonlinear electrodynamics it is possible to remove these singularities by constructing a regular black hole solution [51,52,53,54,55]. Recently, Kruglov has proposed a new model of nonlinear electrodynamics with two parameters \(\beta \) and \(\gamma \) where the the specific range of magnetic field, the causality and unitary principles are satisfied [41]. Moreover, it is shown that there is no singularity of the electric field strength at the origin for the point-like particles and it has a magnetic charge. Moreover, AN Aliev et al. showed the effect of the magnetic field on the black hole space time [56,57,58,59,60].
This paper is organized as follows. In Sect. 2, we briefly review the solution of magnetized black hole and then we calculate its optical geometry and the optical curvature. In Sect. 3, deflection angle of photon using the GBT is studied in the case of magnetized black hole. In Sect. 4, we analysis the deflection angle in details using the graphical analysis. And we concludes in Sect. 4 with a discussion regarding the results obtained from the present work.
2 Weak gravitational lensing and magnetized black hole
The action for the Einstein with a nonlinear electrodynamics (NLED) is given as [41]
where \(k^{2}=8\pi G\equiv M^{-2}_{pl}\), \(M_{pl}\) is for reduced planck mass, G is Newtonian constant and R is Ricci scalar. From above equation we derived the Einstein equations as
Now, we derive the equation of motion for electromagnetic fields by varying (1)
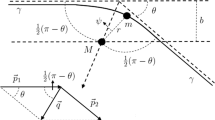
Now, we analyze the static magnetic black hole solution by using the Einstein field equation and equation of motion for electromagnetic field with above equations. In the case of pure magnetic field, Bronnikov showed [51] that when spherical symmetry holds, the invariant is \({\mathcal {F}}=q^{2}/(2r^{2})\), where q is a magnetic charge. In this case, the line element of the static and spherical symmetric space-time is
by assuming both the source and observer are in the equatorial plane likewise trajectory of the null photon is also on the same plane with\((\theta =\frac{\pi }{2})\), we obtain the optical metric as follows
For moving photon in the equatorial plane and null geodesics, \(d s^{2}=0\), we get
Subsequently, we make the transformation into new coordinate u, the metric function \(\zeta (u)\) as
Then the optical metric tensor \({\bar{g}}_{ab}\) is as follows
It is to be noted that \((a,b)\rightarrow (r,\varphi )\) and determinant is \(det{\bar{g}}_{ab}=\frac{r^{2}}{f(r)^{3}}\). Now using Eq.(8), the non-zero Christopher symbols are \(\Gamma ^{r}_{rr}=-\frac{f'(r)}{f(r)}\), \(\Gamma ^{r}_{\varphi \varphi }= \frac{r(rf'(r)-2f(r))}{2}\), \(\Gamma ^{\varphi }_{r\varphi }= \frac{-rf'(r)+2f(r)}{2rf(r)}=\Gamma ^{\varphi }_{\varphi r}\). Hence, we can find the Gaussian optical curvature \({\mathcal {K}}\) [16] as follows
Now, we rewrite Gaussian optical curvature in terms of Schwarzschild radial coordinate r [61]:
By applying Eq. (10) into our metric (6) we obtain the Gaussian optical curvature of photon from magnetized black hole, which yields that
where the function f(r) is [41]
After substituting the value of f(r), we get the value of optical curvature up to leading orders
3 Deflection angle of photon and Gauss–Bonnet theorem
Now, we use the Gauss–Bonnet theorem to derive the deflection angle of photon for magnetized black hole. We apply the Gauss–Bonnet theorem to the region \({\mathcal {M}}_{R}\), stated as [16]
Here \({\mathcal {K}}\) is for Gaussian curvature and the geodesic curvature is k, given as \(k={\bar{g}}(\nabla _{{\dot{\alpha }}}{\dot{\alpha }},\ddot{\alpha })\) in such a way that \({\bar{g}}({\dot{\alpha }},{\dot{\alpha }})=1\), where \(\theta _{j}\) is the representation for exterior angle at the j th vertex and \(\ddot{\alpha }\) is unit acceleration vector. The jump angles become \(\pi /2\) as \(R\rightarrow \infty \) and we get \(\theta _{O}+\theta _{S}\rightarrow \pi \). The Euler characteristic is \({\mathcal {X}}({\mathcal {M}}_{R})=1\), as \({\mathcal {M}}_{R}\) is non singular. Therefore we get
where \(\theta _{j}=\pi \) shows the total jump angle and \(\alpha _{{\bar{g}}}\) is a geodesic; since the Euler characteristic number \({\mathcal {X}}\) is 1. As \(R\rightarrow \infty \) the remaining part yield that \(k(D_{R})=\mid \nabla _{{\dot{D}}_{R}}{\dot{D}}_{R}\mid \). The radial component of the geodesic curvature is given by
At very large R, \(D_{R}:=r(\varphi )=R=const\). Therefore, the first term of equation (17) vanish and \(({\dot{D}}^{\varphi }_{R})^{2}=\frac{1}{\zeta }\). Recalling \(\Gamma ^{r}_{\varphi \varphi }=\frac{r(r f'(r)-2f(r))}{2}\), we get
and it shows that the geodesic curvature is independent of topological defects, \(k(D_{R})\rightarrow R^{-1}\). But from the optical metric (8), we can say that \(dt=Rd\varphi \). Therefore we find that
Taking into account the above results, we obtain
In the weak deflection limit, by assuming that at the zeroth order the light ray is given by \(r(t)=b/\sin \varphi \). Thus by using (14) and (20), the deflection angle becomes [16]
where,
After substituting the leading order term of Gaussian curvature (14) into equation(21), the deflection angle up to second order term is calculated as follows:
4 Graphical analysis
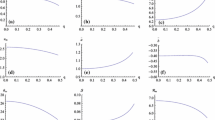
This section is devoted to discuss the graphically behavior of deflection angle \(\Theta \). We also demonstrate the physical significance of these graphs to analyze the impact of correction parameter \(\beta \), BH charge q, and impact parameter b on deflection angle by examining the stability and instability of BH.
4.1 Deflection angle with Impact parameter b
This subsection gives the analysis of deflection angle \(\Theta \) with impact parameter b for different values of correction parameter \(\beta \) and BH charge q in geometrized unit \(8\pi G = 1\).
-
Figure 1 shows the behavior of \(\Theta \) with b for varying q and for fixed value for correction parameter.
-
1.
In figure (i), we examined that the deflection angle exponentially decreases for small variation of q.
-
2.
In figure (ii), we analyzed that the deflection angle gradually decreasing and then eventually goes to infinity for large variation of q which is the unstable state of magnetized BH. Therefore, we conclude that for small values of q the magnetized BH is stable but as q increases it shows the unstable behavior of magnetized BH.
In Fig. 2, indicates the behavior of deflection angle with impact parameter by varying correction parameter \(\beta \).
-
1.
In figure (i), we noticed that the deflection angle decreasing constantly for small values of \(\beta \) but in
-
2.
In figure (ii), as \(\beta \) increases the deflection angle gradually decreasing and then goes to infinity.
-
1.
-
Figure 3 shows the behavior of \(\Theta \) with correction parameter \(\beta \).
-
1.
In figure (i), shows the behavior of \(\Theta \) with \(\beta \), for varying b and fixed q. This shows that when \(b<0\) it gives the uniform negative behavior but for \(b>0\) it behave as a positive slope. We also conclude that for \(4\le b<15\) the behavior is negative slope but for \(b\ge 15\) it gives positive slope.
-
2.
In figure (ii), indicate the behavior of \(\Theta \) with \(\beta \), for the variation of q and fixed b. We examined that the deflection angle is positively increasing with increase of q but for \(5\le q \le 10\) the behavior is negative and then it becomes positive.
In Figure 4, represent the behavior of deflection angle with BH charge q.
-
1.
In figure (i), represents the behavior of \(\Theta \) with q, by varying \(\beta \) and fixed b. We analyzed that the deflection angle initially decreases but as \(\beta \) increases the deflection angle firstly decreases and then increases. We also observe that for \(\beta >20\) the behavior is increasing.
-
2.
In figure (ii), shows the behavior of \(\Theta \) with q, by varying b and fixed \(\beta \). We observed that the deflection angle is increasing for smaller values of b but as b increases the deflection angle become negatively decreasing.
-
1.
The photon lensing in weak field approximation has been studied by many authors [62,63,64,65]. Frolov [66] discussed the collision of particles in the vicinity of horizon of weekly magnetized non-rotating black hole in the presence of the magnetic field Innermost Stable Circular Orbits (ISCO) of charged particles. He demonstrated that for a collision of two particles, one of which is charged and revolving at ISCO and the other is neutral and falling from infinity, the maximal collision energy can be high in the limit of strong magnetic field. He also illustrated that for realistic astrophysical black holes, their ability to play the role of accelerators is in fact quite restricted. Liang [67] calculated the deflection angle in the strong deflection limit and also obtained the angular positions and magnifications of relativistic images as well as the time delay between different relativistic images. He also discussed the influence of the magnetic charge on the black hole gravitational lensing. Recently, Turimov et al. [68] have considered the magnetic field around a gravitational source and illustrated that the split of the Einstein ring, as the counterpart of the Zeeman effect. When the cyclotron frequency approaches to the plasma frequency, the size and the form of the ring change because of the presence of a resonance state. This is a pure magnetic effect and can potentially help to study magnetic fields through gravitational lensing effects. Moreover, they found the deflection angle of a photon moving in an inhomogeneous magnetized plasma in the background of a static compact object and the obtained deflection angle is
where \(\Gamma (x)\) is the gamma function
In our analysis, we study the weak gravitational lensing and obtain the deflection angle of photon in the background of magnetized black hole and analyze the effects of non-linear electrodynamics by means of Gauss–Bonnet theorem. To this end, initially, we set the photon rays on the equatorial plane in the axisymmetric spacetime and evaluate the corresponding optical metric. After that we calculate the Gaussian optical curvature for Gauss–Bonnet theorem. Furthermore, we investigate the impact of correction parameter, black hole charge and impact parameter on deflection angle of photon for magnetized black hole and investigate the effect of non-linear electrodynamics graphically. We conclude that the mass m decreases the deflection angle, while the correction parameter \(\beta \) increases the deflection angle. Also, we prove that the impact parameter b is directly proportional to the deflection angle.
In comparison with the deflection angle computed by Turimov et al. [68], they found the deflection angle of a light ray passing near a magnetized static compact object surrounded by weak inhomogeneous plasma while we have evaluated the deflection angle by using GBT in a weak gravitational lensing for spherically symmetric spacetime incorporating magnetic field and correction parameter \(\beta \).
5 Conclusion
In this paper, we have analyze a model of NLED with parameter \(\beta \). Then, we study the magnetized black hole and obtained the regular black hole solution. After that we calculate the optical Gaussian curvature for magnetized black hole. Then by using Gauss–Bonnet theorem, we calculate the weak gravitational lensing. We obtain the following angle of deflection for magnetized black hole
We conclude that for f(r) if \(r\rightarrow \infty \) the space-time becomes flat, if \(\beta =0\) the NLED model converted into Maxwell’s electrodynamics and the solution becomes RN solution. We have analyzed the behavior of deflection angle w.r.t impact parameter b, correction parameter \(\beta \) and BH charge q.
The results obtained from the analysis of deflection angle given in the paper are summarized as follows:
Deflection angle with respect to impact parameter:
-
In our analysis we have to discussed the behavior of deflection angle, for this we choose different values of BH charge q and fixed correction parameter. For smaller values, the deflection angle gradually decreasing but for large values of q the deflection angle gradually decreases and then goes to infinity.
-
While for fixed q and different values of \(\beta \), the deflection angle constantly decreases for small range of \(\beta \) and gradually decreases for greater values.
-
Thus, we conclude that for smaller values, BH indicates the stability and for large values shows the instability of BH.
Deflection angle with respect to correction parameter:
-
The behavior of \(\Theta \) w.r.t \(\beta \), for fixed q and varying b, positive behavior can be observed only for \(b>0\) except \(4\le b<15\).
-
The behavior of \(\Theta \) w.r.t \(\beta \), for fixed b and varying q, the behavior is positively increasing for \(q>0\) except \(5\le q\le 10\).
Deflection angle with respect to black hole charge:
-
The behavior of \(\Theta \) w.r.t q, for fixed b and varying \(\beta \), the deflection angle initially decreases but with the increase of \(\beta \), the deflection angle firstly decreases and then increases. For \(\beta >20\) the deflection angle positively increases.
-
The behavior of \(\Theta \) w.r.t q, for fixed \(\beta \) and choose different values of b, the deflection angle positively increases for small b and negatively decreases for greater b.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ Comment: This is a theoretical study and no experimental data has been listed.]
References
A. Einstein, Lens-like action of a star by the deviation of light in the gravitational field. Science 84, 506 (1936)
B.P. Abbott et al. [LIGO Scientific and Virgo Collaborations], Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 116(6), 061102 (2016)
S.S. Li, S. Mao, Y. Zhao, Y. Lu, Gravitational lensing of gravitational waves: a statistical perspective. Mon. Not. R. Astron. Soc. 476(2), 2220 (2018)
J. Soldner, Ueber die Ablenkung eines Lichtstrals von seiner geradlinigen Bewegung, durch die Attraktion eines Weltkörpers, an welchem er nahe vorbei geht. Berliner Astronomisches Jahrbuch, 161–172.cc (1804)
F.W. Dyson, A.S. Eddington, C. Davidson, A determination of the deflection of light by the sun’s gravitational field, from observations made at the total eclipse of May 29, 1919. Phil. Trans. R. Soc. Lond. A 220, 291 (1920)
D. Valls-Gabaud, The conceptual origins of gravitational lensing. AIP Conf. Proc. 861(1), 1163 (2006)
M. Bartelmann, P. Schneider, Weak gravitational lensing. Phys. Rep. 340, 291 (2001)
M. Bartelmann, Gravitational lensing. Class. Quant. Gravit. 27, 233001 (2010)
C.R. Keeton, C.S. Kochanek, E.E. Falco, The optical properties of gravitational lens galaxies as a probe of galaxy structure and evolution. Astrophys. J. 509, 561 (1998)
E.F. Eiroa, G.E. Romero, D.F. Torres, Reissner–Nordstrom black hole lensing. Phys. Rev. D 66, 024010 (2002)
S. Mao, B. Paczynski, Gravitational microlensing by double stars and planetary systems. Astrophys. J. 374, L37 (1991)
V. Bozza, Gravitational lensing in the strong field limit. Phys. Rev. D 66, 103001 (2002)
E. Gallo, O.M. Moreschi, Gravitational lens optical scalars in terms of energy-momentum distributions. Phys. Rev. D 83, 083007 (2011)
G. Crisnejo, E. Gallo, Expressions for optical scalars and deflection angle at second order in terms of curvature scalars. Phys. Rev. D 97(8), 084010 (2018)
M. Sharif, S. Iftikhar, Strong gravitational lensing in non-commutative wormholes. Astrophys. Space Sci. 357(1), 85 (2015)
G.W. Gibbons, M.C. Werner, Applications of the Gauss–Bonnet theorem to gravitational lensing. Class. Quant. Gravit. 25, 235009 (2008)
M.C. Werner, Gravitational lensing in the Kerr–Randers optical geometry. Gen. Relat. gravit. 44, 3047 (2012)
A. Ishihara, Y. Suzuki, T. Ono, T. Kitamura, H. Asada, Gravitational bending angle of light for finite distance and the Gauss–Bonnet theorem. Phys. Rev. D 94(8), 084015 (2016)
G. Crisnejo, E. Gallo, Weak lensing in a plasma medium and gravitational deflection of massive particles using the Gauss–Bonnet theorem. A unified treatment. Phys. Rev. D 97(12), 124016 (2018)
K. Jusufi, M.C. Werner, A. Banerjee, A. Övgün, Light deflection by a rotating global monopole spacetime. Phys. Rev. D 95(10), 104012 (2017)
I. Sakalli, A. Ovgun, Hawking radiation and deflection of light from rindler modified schwarzschild black hole. EPL 118(6), 60006 (2017)
K. Jusufi, A. Övgün, Gravitational lensing by rotating wormholes. Phys. Rev. D 97(2), 024042 (2018)
T. Ono, A. Ishihara, H. Asada, Gravitomagnetic bending angle of light with finite-distance corrections in stationary axisymmetric spacetimes. Phys. Rev. D 96(10), 104037 (2017)
K. Jusufi, A. Övgün, A. Banerjee, Light deflection by charged wormholes in Einstein-Maxwell-dilaton theory. Phys. Rev. D 96(8), 084036 (2017)
A. Övgün, G. Gyulchev, K. Jusufi, Weak gravitational lensing by phantom black holes and phantom wormholes using the Gauss–Bonnet theorem. Ann. Phys. 406, 152 (2019)
K. Jusufi, I. Sakalli, A. Övgün, Effect of lorentz symmetry breaking on the deflection of light in a cosmic string spacetime. Phys. Rev. D 96(2), 024040 (2017)
H. Arakida, Light deflection and GaussBonnet theorem: definition of total deflection angle and its applications. Gen. Relat. Gravit. 50(5), 48 (2018)
T. Ono, A. Ishihara, H. Asada, Deflection angle of light for an observer and source at finite distance from a rotating wormhole. Phys. Rev. D 98(4), 044047 (2018)
K. Jusufi, A. Övgün, Effect of the cosmological constant on the deflection angle by a rotating cosmic string. Phys. Rev. D 97(6), 064030 (2018)
A. Övgün, K. Jusufi, I. Sakalli, Exact traversable wormhole solution in bumblebee gravity. Phys. Rev. D 99(2), 024042 (2019)
K. Jusufi, A. Övgün, J. Saavedra, Y. Vasquez, P.A. Gonzalez, Deflection of light by rotating regular black holes using the Gauss–Bonnet theorem. Phys. Rev. D 97(12), 124024 (2018)
A. Övgün, Light deflection by Damour–Solodukhin wormholes and Gauss–Bonnet theorem. Phys. Rev. D 98(4), 044033 (2018)
A. Övgün, K. Jusufi, I. Sakalli, Gravitational lensing under the effect of Weyl and bumblebee gravities: applications of Gauss–Bonnet theorem. Ann. Phys. 399, 193 (2018)
A. Övgün, Deflection angle of photon through dark matter by black holes and wormholes using the Gauss–Bonnet theorem. Universe 5(5), 115 (2019)
A. Övgün, I. Sakalli, J. Saavedra, Weak gravitational lensing by Kerr–MOG black hole and Gauss–Bonnet theorem. arXiv:1806.06453 [gr-qc]
A. Övgün, I. Sakalli, J. Saavedra, Shadow cast and deflection angle of Kerr–Newman–Kasuya spacetime. JCAP 1810(10), 041 (2018)
T. Ono, A. Ishihara, H. Asada, Deflection angle of light for an observer and source at finite distance from a rotating global monopole. Phys. Rev. D 99(12), 124030 (2019)
A. Övgün, Weak gravitational lensing of regular black holes with cosmic strings using the Gauss–Bonnet theorem. Phys. Rev. D 99(10), 104075 (2019)
Wajiha Javed, Rimsha Babar, A. Övgün, The effect of the Brane–Dicke coupling parameter on weak gravitational lensing by wormholes and naked singularities. Phys. Rev. D 99(8), 084012 (2019)
A. Övgün, İ. Sakallı, Deriving Hawking radiation via Gauss-Bonnet Theorem: an alternative way. arXiv:1902.04465 [hep-th]
S.I. Kruglov, Magnetized black holes and nonlinear electrodynamics. Int. J. Mod. Phys. A 32(23n24), 1750147 (2017)
S.I. Kruglov, On a model of magnetically charged black hole with nonlinear electrodynamics. Universe 4(5), 66 (2018)
S.I. Kruglov, Nonlinear electrodynamics and magnetic black holes. Ann. Phys. 529(8), 1700073 (2017)
S.I. Kruglov, BornInfeld-type electrodynamics and magnetic black holes. Ann. Phys. 383, 550 (2017)
S.I. Kruglov, Black hole as a magnetic monopole within exponential nonlinear electrodynamics. Ann. Phys. 378, 59 (2017)
S.I. Kruglov, Notes on BornInfeld-type electrodynamics. Mod. Phys. Lett. A 32(36), 1750201 (2017)
S.I. Kruglov, Asymptotic Reissner–Nordstrm solution within nonlinear electrodynamics. Phys. Rev. D 94(4), 044026 (2016)
S.I. Kruglov, Nonlinear arcsin-electrodynamics and asymptotic Reissner–Nordstrm black holes. Ann. Phys. 528, 588 (2016)
M. Novello, V.A. De Lorenci, J.M. Salim, R. Klippert, Geometrical aspects of light propagation in nonlinear electrodynamics. Phys. Rev. D 61, 045001 (2000)
M. Novello, J.M. Salim, V.A. De Lorenci, E. Elbaz, Nonlinear electrodynamics can generate a closed space—like path for photons. Phys. Rev. D 63, 103516 (2001)
K.A. Bronnikov, Regular magnetic black holes and monopoles from nonlinear electrodynamics. Phys. Rev. D 63, 044005 (2001)
E. Ayon-Beato, A. Garcia, Regular black hole in general relativity coupled to nonlinear electrodynamics. Phys. Rev. Lett. 80, 5056 (1998)
E. Ayon-Beato, A. Garcia, Nonsingular charged black hole solution for nonlinear source. Gen. Relat. Gravit. 31, 629 (1999)
M.E. Rodrigues, MVdS Silva, Bardeen regular black hole with an electric source. JCAP 1806(06), 025 (2018)
S.A. Hayward, Formation and evaporation of regular black holes. Phys. Rev. Lett. 96, 031103 (2006)
A.N. Aliev, D.V. Galtsov, Magnetized black holes. Sov. Phys. Usp. 32, 75 (1989)
A.N. Aliev, Rotating black holes in higher dimensional Einstein–Maxwell gravity. Phys. Rev. D 74, 024011 (2006)
A.N. Aliev, Gyromagnetic ratio of charged Kerr-Anti-de sitter black holes. Class. Quant. Gravit. 24, 4669 (2007)
A.N. Aliev, V.P. Frolov, Five-dimensional rotating black hole in a uniform magnetic field: the gyromagnetic ratio. Phys. Rev. D 69, 084022 (2004)
A.N. Aliev, N. Ozdemir, Motion of charged particles around a rotating black hole in a magnetic field. Mon. Not. R. Astron. Soc. 336, 241 (2002)
D. Bao, S. Chern, Z. Shen, An introduction to Riemann–Finsler geometry (Springer, New York, 2000)
B. Paczynski, Gravitational microlensing by the galactic halo. Astrophys. J. 304, 1 (1986)
C. Alcock et al. [Supernova Cosmology Project Collaboration], Possible Gravitational Microlensing of a Star in the Large Magellanic Cloud. Nature 365, 621 (1993)
E. Aubourg et al., Evidence for gravitational microlensing by dark objects in the galactic halo. Nature 365, 623 (1993)
A. Udalski, M. Szymanski, J. Kaluzny, M. Kubiak, W. Krzeminski, M. Mateo, G.W. Preston, B. Paczynski, The optical gravitational lensing experiment. Discovery of the first candidate microlensing event in the direction of the Galactic Bulge. Acta Astron. 43, 289 (1993)
V.P. Frolov, Weakly magnetized black holes as particle accelerators. Phys. Rev. D 85, 024020 (2012)
J. Liang, Regular magnetic black hole gravitational lensing. Chin. Phys. Lett. 34(5), 050401 (2017)
B. Turimov, B. Ahmedov, A. Abdujabbarov, C. Bambi, Gravitational lensing by magnetized compact object in the presence of plasma. arXiv:1802.03293 [gr-qc]
Acknowledgements
This work was supported by Comisión Nacional de Ciencias y Tecnología of Chile through FONDECYT Grant \(N^\mathrm {o}\) 3170035 (A. Ö.).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Javed, W., Abbas, J. & Övgün, A. Deflection angle of photon from magnetized black hole and effect of nonlinear electrodynamics. Eur. Phys. J. C 79, 694 (2019). https://doi.org/10.1140/epjc/s10052-019-7208-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-019-7208-3