1 Introduction

In this paper we would like to study holographic complexity for Jackiw–Teitelboim (JT) gravity [1, 2] using the “complexity = action” proposal (CA) [3, 4]. According to this proposal the holographic complexity of a holographic state is given by the on-shell action evaluated on a bulk region known as the “Wheeler-De Witt” (WDW) patch

$$\begin{aligned} {{{\mathcal {C}}}}(\Sigma )=\frac{I_{\mathrm{WDW}}}{\pi \hbar }. \end{aligned}$$
(1.1)

Here the WDW patch is defined as the domain of dependence of any Cauchy surface in the bulk whose intersection with the asymptotic boundary is the time slice \(\Sigma \).

We note that the holographic complexity for JT gravity has been recently studied in [5] where the authors have observed that a naive computation of the complexity leads to a counterintuitive result. Namely the complexity approaches a constant at the late time, though one would expect to get a linear growth at the late time. To overcome the problem the authors of [5] have considered the case where the corresponding JT gravity was obtained from a four dimensional Maxwell–Einstein gravity admitting charged black hole solutions. Therefore the desired result was obtained with the cost of adding charge to the model.

Actually the problem arises due to the fact that in the near extremal limit of charged black holes one usually has to deal with geometries containing an \({\hbox {AdS}}_2\) factor. In this case a naive computation of complexity gives raise to a constant at the late time. A remedy to resolve the problem has been also proposed in [6] where it was shown that setting a UV cutoff at the boundary would automatically induce a cutoff behind the horizon that removes some part of the space time inside the horizon. This indeed naturally leads to complexity that has desired linear growth at the late time for a model admitting \({\hbox {AdS}}_2\) solution with constant Dilaton.

It is important to mention that the result of [6] leading to the behind the horizon cutoff relies on two facts. The first one is that according to explicit computations using CA proposal the late time behavior is not sensitive to the UV cutoff. The second one is that according to Lloyd’s bound [7] the late time behavior is given by twice of energy of the system. In fact we should emphases that in order to reach our conclusion the actual value of bound is not crucial. The important fact is that the late time behavior is governed by the physical charges defined at the boundary; such as mass or energy that are affected by UV cutoff.

The aim of the present paper is to compute holographic complexity for JT gravity using the procedure of [6]. The model has a solution with an \({\hbox {AdS}}_2\) geometry supported by a linear Dilation. Unlike the cases studied in [6] in the present case where the Dilaton is not constant the complexity has non-trivial time dependence that leads to violation of Lloyld’s bound [7] (see e.g. [8]). It is worth noting that the JT gravity we will be considering does not necessarily have a higher dimensional counter part.

It has been proposed (see for example [9,10,11]) that this model could provide a holographic dual for the nearly conformal dynamics of the Sachdev–Ye-Kitaev model [12, 13]. Therefore it might be interesting to study holographic complexity for JT gravity which in turns could enrich our knowledge on gravity dual of Sachdev–Ye-Kitaev model.

The organization of the paper is as follows. In the next section we shall study complexity for JT gravity. In section three we will compute complexity for a general two dimensional Dilaton-gravity for the case where the solution consists of small fluctuations above an \({\hbox {AdS}}_2\) geometry with constant Dilaton. We will see that in order to get the desired results it is crucial to consider the contribution of certain counter terms evaluated on the behind the horizon cutoff. The last section is devoted to conclusions.

2 CA complexity for Jackiw–Teitelboim gravity

In this section we study holographic complexity for JT gravity whose action may by written as followsFootnote 1

$$\begin{aligned} I= & {} \frac{1}{8 G}\int d^{2}x\sqrt{-g}\,\phi \left( R+\frac{2}{\ell ^2} \right) \nonumber \\&+\frac{1}{4G}\int dt \sqrt{-h}\,\phi \left( K-\frac{1}{\ell }\right) \,, \end{aligned}$$
(2.1)

where K is extrinsic curvature of the time like boundary whose trace of induced metric is \( -h\). The first term in the boundary part of the action is required to maintain the variational principle well imposed, while the second there is needed to get quantities, such as free energy, finite. Although this term does not alter the equations of motion, as we will see has a crucial role in the holographic complexity.

The equations of motion of JT gravity obtained from the above action are

$$\begin{aligned} R=-\frac{2}{\ell ^2},\quad \nabla ^2 \phi =\frac{2}{\ell ^2}\phi . \end{aligned}$$
(2.2)

These equations admit the following linear Dilaton \(AdS_2\) solution

$$\begin{aligned} ds^2=-f(r)\,dt^2+\frac{dr^2}{f(r)}, \quad \phi (r)=\frac{r}{\ell }, \end{aligned}$$
(2.3)

where \(f(r)=\frac{1}{\ell ^2}(r^2-r_h^2)\). This might be thought of as a two dimensional black hole whose entropy and Hawking temperature are given by

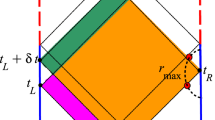
$$\begin{aligned} S=\frac{\pi }{2G} \frac{r_h}{\ell }, \quad T=\frac{r_h}{2\pi \ell ^2}. \end{aligned}$$
(2.4)

Now the aim is to compute complexity for this model. To do so, one should evaluate on shell action on the WDW patch shown in the Fig. 1. The null boundaries of the corresponding WDW patch are given by

$$\begin{aligned} {\mathrm{right \,side}}&t=t_R+r^*(r_{\mathrm{Max}})-r^*(r), \nonumber \\&t=t_R-r^*(r_{\mathrm{Max}})+r^*(r), \nonumber \\ {\mathrm{left \,side}}&t=-t_L+r^*(r_{\mathrm{Max}})-r^*(r), \nonumber \\&t=-t_L-r^*(r_{\mathrm{Max}})+r^*(r), \end{aligned}$$
(2.5)

where \(t_L, t_R\) the time coordinates associated with the left and right boundaries. Here \(r_{\mathrm{Max}}\) is a UV cutoff. We would like to compute complexity for a state given at the time \(\tau =t_L+t_R\). In this notation the joint point \(r_m\) shown in the Fig. 1 is determined by

$$\begin{aligned} \tau =2(r^*(r_{\mathrm{Max}})-r^*(r_{m})). \end{aligned}$$
(2.6)
Fig. 1
figure 1

Penrose diagram of \({\hbox {AdS}}_2\) geometry. The green area is covered by global coordinate while the diamond shown by dashed lines is covered by Rindler coordinates.The WDW patch is shown by blue color. The inside cutoff \(r_0\) is given by in terms of UV cutoff by \(r_0 r_{\mathrm{Max}}^2=r_h^3\) at leading order. This figure is taken from the Ref. [6]

Full size image

Actually in general one could have had two joint points associated with the WDW patch under consideration; one at \(r_m\) and the other at \(r_{m'}\) shown by dashed lines in the Fig. 1. We note, however, that as soon as we set the UV cutoff to regularize the on shell action, there will be a cutoff behind the horizon whose value is fixed by the UV cutoff [6]. More precisely at leading order one has \(r_0 \sim \frac{{r_h^3}}{r_{\mathrm{Max}}^2}\). This cutoff prevents us to have access to the joint point \(r_{m'}\) and the corresponding WDW patch is cut at \(r=r_0\).

To proceed to compute the on shell action we note that from the equations of motion the bulk part of the action (2.1) gives zero contribution to the on shell action. Moreover, using the Affine parameter for the null directions, there is no contribution from the null boundaries either. Therefore as far as the boundary term is concerned we are left with one space like boundary at \(r=r_0\)Footnote 2

$$\begin{aligned} I^{\mathrm{surf}}= & {} -\frac{1}{4G}\int _{-t_L-r^*(r_\mathrm{Max})+r^*(r)}^{t_R+r^*(r_{\mathrm{Max}})-r^*(r)} dt \sqrt{-h}\,\phi \left( K-\frac{1}{\ell }\right) \bigg |_{r_0} \nonumber \\= & {} \frac{r_0(r_0+r_h)}{4G \ell ^3} \bigg (\tau +2 (r^*(r_{\mathrm{Max}})-r^*(r_0))\bigg )\,. \end{aligned}$$
(2.7)

It is important to note that the overall minus sign is due to the fact that the boundary we are considering is a space like surface [18].

There is also certain terms associated with joint points where a null boundary intersects with other null, space like or time like boundaries [18, 19]. In the present case we have five joint points two of which at the UV cutoff surface, two at the cutoff behind the horizon and, one at the joint point \(r_m\). The corresponding contributions are given by

$$\begin{aligned} I^{\mathrm{joint}}=\frac{1}{4G}\sum _{\mathrm{joint}} \mathrm{Sign(joint)}\,\phi (r)\log \eta , \end{aligned}$$
(2.8)

where \(\eta \) is the inner product of normal vectors of the corresponding intersecting boundaries. Denoting the null vectors and normal vector to the space like boundary \(r_0\), respectively, by

$$\begin{aligned} k_1= & {} \alpha \left( \partial _t-\frac{1}{f(r)}\partial _r\right) ,\quad k_2 =\beta \left( \partial _t+\frac{1}{f(r)}\partial _r\right) , \nonumber \\ k_0= & {} \frac{1}{\sqrt{f(r_0)}}\partial _r \end{aligned}$$
(2.9)

the contribution of joint points reads

$$\begin{aligned} I^{\mathrm{joint}}= & {} \frac{1}{4G}\left( \phi (r_m)\log \bigg |\frac{\alpha \beta }{f(r_m)}\bigg |+\phi (r_0) \log \bigg |\frac{\alpha }{ \sqrt{f(r_{0})}}\bigg | \right. \nonumber \\&+\phi (r_0) \log \bigg |\frac{\beta }{ \sqrt{f(r_{0})}}\bigg | \nonumber \\&\left. -2\phi (r_{\mathrm{Max}}) \log \bigg |\frac{\alpha \beta }{f(r_{\mathrm{Max}})}\bigg |\right) \nonumber \\= & {} \frac{1}{4G\ell }\left( r_m\log \bigg |\frac{\alpha \beta }{ f(r_m)}\bigg |+r_0 \log \bigg |\frac{\alpha \beta }{{f(r_{0})}}\bigg | \right. \nonumber \\&\left. -2r_{\mathrm{Max}} \log \bigg |\frac{\alpha \beta }{ f(r_{\mathrm{Max}})}\bigg |\right) \nonumber \\= & {} \frac{1}{4G\ell }\bigg (2r_{\mathrm{Max}} \log |f(r_{\mathrm{Max}})|-r_m\log | f(r_m)|\bigg ) \nonumber \\&+\frac{1}{4G\ell } (r_m-2r_{\mathrm{Max}})\log {\alpha \beta }\,. \end{aligned}$$
(2.10)

Here \(\alpha \) and \(\beta \) are two free parameters appearing due to the ambiguity of normalization of null vectors. Of course there is a boundary term that should be added to remove this ambiguity [18]. In the present case the corresponding boundary term is given by

$$\begin{aligned} I^{\mathrm{amb}}=\frac{1}{4G}\int d\lambda \, \partial _\lambda \phi \log |\ell \partial _\lambda \phi |. \end{aligned}$$
(2.11)

where \(\lambda \) is the null coordinate defined on the null direction. Using the Affine parameter for the null direction and taking into account the contribution of all null boundaries one finds

$$\begin{aligned} I^{\mathrm{amb}}=-\frac{1}{4G\ell } (r_m-2r_{\mathrm{Max}})\log {\alpha \beta }\,, \end{aligned}$$
(2.12)

that cancels the last term in the above equation leading to the following expression for the total on shell action

$$\begin{aligned} I^{\mathrm{total}}=-\frac{1}{4G\ell } r_m\log | f(r_m)|\,. \end{aligned}$$
(2.13)

Note that to find the final result we have also taken the \(r_0\rightarrow 0\) limit that is equivalent to the limit of \(r_\mathrm{Max} \rightarrow \infty \). It is then easy to compute the time derivative of the on shell action

$$\begin{aligned} \frac{dI^{\mathrm{total}}}{d\tau }=\frac{1}{4G\ell ^3} \left( r_m^2+\frac{r_m^2-r_h^2}{2}\log | f(r_m)| \right) , \end{aligned}$$
(2.14)

that may be recast into the following form

$$\begin{aligned} \frac{dI^{\mathrm{total}}}{d\tau }=2M \left( \frac{r_m^2}{r_h^2}+\frac{r_m^2-r_h^2}{2r_h^2}\log | f(r_m)| \right) \,, \end{aligned}$$
(2.15)

where \(M=\frac{r_h^2}{8G\ell ^3}\). It is worth mentioning that the above complexity rate of growth becomes 2M at two points given by \(r_m=r_h\sqrt{|1-\frac{\ell ^2}{e^2 r_h^2}|}\) and \(r=r_h\) and has a maximum between these two values (here e is the Euler number defined by \(\log e=1\)). Therefore the Lloyd’s bound defined by 2M will be violated as the growth rate approaches the Lloyd’s bound from above at the late time.

3 CA complexity for a general 2D gravity

In this section we shall study holographic complexity for a general two dimensional Dilaton-Einstein gravity whose action is given by (see for example [20])

$$\begin{aligned} I= & {} \frac{1}{8G}\int d^2x\,\sqrt{-g}\,\bigg (\Phi R+V(\Phi )\bigg ) \nonumber \\&+\frac{1}{4G}\int dt\,\sqrt{-h} \Phi \left( K-\frac{1}{\ell }\right) , \end{aligned}$$
(3.1)

where \(V(\Phi )\) is a general potential for the Dilaton field. This is an action which may be obtained from higher dimensional Maxwell–Einstein gravities by dimensional reduction into two dimensions.

We are interested in a solution that is nearly \({\hbox {AdS}}_2\) geometry with constant Dilaton. This may be found by expanding the Dilaton field around a constant value \(\phi _0\). In order to guarantee an \({\hbox {AdS}}_2\) geometry one should have

$$\begin{aligned} \ell ^2=\frac{2}{V'(\phi _0)}, \end{aligned}$$
(3.2)

where \(\ell \) is a constant that is the radius of the corresponding AdS geometry. Note also that the constant \(\phi _0\) is a solution of \(V(\phi _0)=0\). Let us now consider solutions of the model for small fluctuation above the constant Dilaton solution

$$\begin{aligned} \Phi =\phi _0+\phi \,. \end{aligned}$$
(3.3)

Expanding the action above the constant Dilaton at leading order in \(\phi \) one findsFootnote 3

$$\begin{aligned} I= & {} \frac{1}{8G}\int d^2x\,\sqrt{-g}\,\phi _0 R \nonumber \\&+ \frac{1}{4G}\int _{\mathrm{boundary}} dt \sqrt{-h}\,\phi _0\bigg (K-\frac{1}{\ell }\bigg ) \nonumber \\&+\frac{1}{8G}\int d^2x\sqrt{-g}\,\phi \left( R+\frac{2}{\ell ^2}\right) \nonumber \\&+\frac{1}{4G}\int _{\mathrm{boundary}} dt \sqrt{-h}\,\phi \bigg (K-\frac{1}{\ell }\bigg )\,. \end{aligned}$$
(3.4)

It is then clear that the part controlling the dynamics of the fluctuations above the constant Dilaton is given by JT gravity we have considered in the previous section. The first part of the action is topological that does not contribute to the equations of motion, though has non-trivial contribution to the physical quantities such as entropy. In the following we will also see that this topological term give an important contribution to the complexity when its counter term is evaluated on the cutoff surface behind the horizon.

The equations of motion of the above action are given by (2.2) and therefore the linear Dilaton solution (2.3) is also a solution of the model under consideration. Now the aim is to compute complexity for this solution. It is, however, evident that the contribution of the dynamical part is exactly the same as that we have obtained in the previous section. Therefore in what follows we just need to compute the contribution of topological terms given in the first line of the Eq. (3.4).

To proceed let us again start with the bulk part. In this case, setting \(R=-\frac{2}{\ell ^2}\), one gets

$$\begin{aligned} I^{\mathrm{bulk}}_0= & {} -\frac{\phi _0}{4G\ell ^2}\bigg (\int _{r_{0}}^{r_h} dr \left( \tau +2(r^*(r_{\mathrm{Max}}) -r^*(r))\right) \nonumber \\&+2\int ^{r_{\mathrm{Max}}}_{r_h} dr \, 2\left( r^*(r_{\mathrm{Max}})-r^*(r)\right) \nonumber \\&+\int _{r_{m}}^{r_h} dr \left( -\tau +2(r^*(r_\mathrm{Max})-r^*(r))\right) \bigg ), \end{aligned}$$
(3.5)

that can be recast to the following form by making use of an integration by parts

$$\begin{aligned} I^{\mathrm{bulk}}_0= & {} -\frac{\phi _0}{4G}\bigg (2\log | f(r_{\mathrm{Max}})|-\log | f(r_m)|-\log | f(r_{0})| \nonumber \\&\quad -r_0\left( \tau +2(r^*(r_\mathrm{Max})-r^*(r_0))\right) \bigg )\,. \end{aligned}$$
(3.6)

The boundary contributions associated with null boundaries are still zero when Affine parametrization is used. Of course in the present case we have a apace like boundary whose contribution is

$$\begin{aligned} I^{\mathrm{surf}}_0= & {} -\frac{\phi _0}{4G}\int dt \sqrt{-h}\left( K_s-\frac{1}{\ell }\right) \bigg |_{r_0} \nonumber \\= & {} \frac{\phi _0}{4G\ell ^2} ( r_0+r_h)\left( \tau +2 (r^*(r_{\mathrm{Max}})-r^*(r_0))\right) . \end{aligned}$$
(3.7)

As for joint points we have

$$\begin{aligned} I^{\mathrm{joint}}_0= & {} \frac{\phi _0}{4G}\left( \log \bigg |\frac{\alpha \beta }{ f(r_m)}\bigg | + \log \bigg |\frac{\alpha }{ \sqrt{f(r_{0})}}\bigg | \right. \nonumber \\&\left. +\log \bigg |\frac{\beta }{ \sqrt{f(r_{0})}}\bigg | -2\log \bigg |\frac{\alpha \beta }{f(r_{\mathrm{Max}})}\bigg |\right) \nonumber \\= & {} \frac{\phi _0}{4G}\bigg (2\log | f(r_{\mathrm{Max}})| -\log | f(r_m)| \nonumber \\&-\log | f(r_0)|\bigg ). \end{aligned}$$
(3.8)

Now putting all terms together and taking \(r_0\rightarrow 0\) limit one arrives at

$$\begin{aligned} I_0=\frac{\phi _0r_h}{4G\ell ^2} \left( \tau +2 (r^*(r_\mathrm{Max})-r^*(r_0))\right) , \end{aligned}$$
(3.9)

as the contribution of the topological terms. Therefore to find the total on shell action one should add this term to that we have obtained in the previous section for the JT gravity

$$\begin{aligned} I^{\mathrm{total}}= & {} -\frac{1}{4G\ell } r_m\log | f(r_m)| \nonumber \\&+\frac{\phi _0r_h}{4G\ell ^2} \left( \tau +2 (r^*(r_\mathrm{Max})-r^*(r_0))\right) . \end{aligned}$$
(3.10)

Thus we get

$$\begin{aligned} \frac{dI^{\mathrm{total}}}{d\tau }= & {} \frac{\phi _0r_h}{4G\ell ^2} +\frac{1}{4G\ell ^3} \nonumber \\&\times \left( r_m^2+\frac{r_m^2-r_h^2}{2}\log | f(r_m)|\right) , \end{aligned}$$
(3.11)

that approaches a constant at the late time

$$\begin{aligned} \frac{dI^{\mathrm{total}}}{d\tau }=\frac{r_h}{4G\ell ^2} \left( \phi _0+\frac{r_h}{\ell }\right) . \end{aligned}$$
(3.12)

The first term is indeed the contribution of near extremity and the second term comes from the fluctuations above it.

To further explore the result, it is illustrative to consider an explicit example where the form of potential is known. To proceed let us consider the following potential [21]

$$\begin{aligned} V(\Phi )=\frac{1}{L^2}\left( (2\Phi )^{-\frac{1}{2}}-Q^2(2\Phi )^{-\frac{3}{2}}\right) , \end{aligned}$$
(3.13)

where Q and L are free dimensionless and dimensionful parameters, respectively. Indeed if one thinks of the model as a two dimensional gravity obtained from a four dimensional Maxwell–Einstein gravity by a dimensional reduction, Q is related to the charge of a four dimensional charged black hole and L is related to the four dimensional Newton constant. It is then easy to see that

$$\begin{aligned} \phi _0=\frac{Q^2}{2},\quad \ell =L Q^{\frac{3}{2}}. \end{aligned}$$
(3.14)

Therefore from (3.12) one gets the following rate of growth

$$\begin{aligned} \frac{dI}{d\tau }=S_0T+\frac{\pi \ell }{G} T^2. \end{aligned}$$
(3.15)

where \(S_0=\frac{\pi Q^2}{4G}\) is the entropy of extremal black hole. Indeed this is the complexity for a near extremal black hole. We note that up to a numerical factor the result is in agreement with that found in [5].

4 Conclusions

In this paper we have studied holographic complexity for JT gravity, where we have seen that the corresponding complexity exhibits linear growth at the late time. Of course to get the consistence results we have considered certain crucial points.

The first point we have considered was the observation that a UV cutoff would set a cutoff behind the horizon. In other words as soon as we regularized the UV modes with a cutoff, this will automatically remove certain models behind the horizon. In particular in the present case the contribution of the joint point associated with \(r_{m'}\) ( shown by dashed lines in Fig. 1) will be removed from the on shell action. Instead we will have to consider the contribution of a surface term associated with the space like boundary sets by the behind the horizon cutoff. Indeed this point was crucial to get the right late times linear growth.

Another observation we have made is the fact that boundary terms (including counter terms) are important in order to get a consistent result. Actually complexity is a quantity that is sensitive to boundary terms. In fact the counter term given in the topological part of the action (3.4), when evaluated on the space like surface, was needed in order to get the extremal contribution to the complexity. Without this term we would not have gotten the term proportional to \(\phi _0\) in the growth rate of complexity. It is worth noting that, indeed, this was also the observation made in [5], where the authors have shown that the contribution of a certain boundary term is crucial to get the physically expected result.Footnote 4

Actually it seems that the boundary term considered in the reference [5] might be related to what we have considered in the present paper. To be more concrete, note that the extra boundary term taken into account in [5] may be written as follows (see equation (7.61) of the cited paper)

$$\begin{aligned} \frac{Q^2}{L^2}\int d^2x \,\sqrt{-g}\,(2\Phi )^{-\frac{3}{2}}, \end{aligned}$$
(4.1)

that, for the extremal limit where \(\Phi =\phi _0\) using the Eq. (3.14), can be recast into the following form

$$\begin{aligned} 2\phi _0 \int d^2x\sqrt{-g} \frac{1}{\ell ^2}. \end{aligned}$$
(4.2)

It is then easy to compute this term over the WDW patch depicted in the Fig. 1. Doing so, one arrives at

$$\begin{aligned} -\frac{\phi _0}{4G}\log |f(r_m)|, \end{aligned}$$
(4.3)

which at the late time leads to the complexity growth \(\frac{\phi _0r_h}{4G\ell ^2}\), in agreement with the first term in (3.12). Note that in order to compare this term with our result we have used our convention by restoring the factor 4G in the above equation. It would be interesting to further explore this comparison in more details.