Full NLO corrections to 3-jet production and $\mathbf {R_{32}}$ at the LHC

Abstract

We present the evaluation of the complete set of NLO corrections to three-jet production at the LHC. To this end we consider all contributions of $\mathcal{{O}}(\alpha _s^n\alpha ^m)$ with $n+m=3$ and $n+m=4$. This includes in particular also subleading Born contributions of electroweak origin, as well as electroweak virtual and QED real-radiative corrections. As an application we present results for the three- over two-jet ratio $R_{32}$. While the impact of non-QCD corrections on the total cross section is rather small, they can exceed $-10\%$ for high jet transverse momenta. The $R_{32}$ observable turns out to be very stable against electroweak corrections, receiving absolute corrections below $5\%$ even in the high-$p_T$ region.

1 Introduction

Jet-production processes make up the most abundant final states in hadron–hadron collisions, as carried out at the Large Hadron Collider (LHC). They are of great importance for the determination of the strong-coupling constant and provide a central ingredient to precise determinations of parton density functions (PDFs). At the same time pure-jet final states constitute promising search grounds for physics beyond the Standard Model, when looking for resonance peaks or an excess of events in the tails of transverse-momentum-type distributions.

Besides being of high phenomenological relevance, jet-production processes serve as benchmark for various types of perturbative calculations including fixed-order evaluations, all-orders resummations and parton-shower simulations. Already the two-jet production channel features quarks and gluons in the initial and final states and correspondingly various types of spin- and color-correlations. Beyond the leading order there arise infrared singularities both in the virtual and real corrections that need to be properly treated. Further, sensitivity to the actual jet criterion used to define the cross section emerges. Beyond perturbation theory, there are important corrections from the fragmentation of final-state partons into hadrons and beam-remnant interactions such as multi-parton scatterings.

For hadro-production the next-to-leading order (NLO) QCD corrections are known to up to five-jet final states [1,2,3,4,5]. The computation of the QCD next-to-next-to leading order (NNLO) corrections to dijet production has recently been completed [6], resulting in significantly reduced scale uncertainties in the predictions, paving the way to precision analyses of LHC dijet data. Dedicated studies on the combination of NLO QCD calculations with parton-shower simulations for dijet production have been presented in [7, 8].

To further improve the theoretical accuracy besides QCD also electroweak (EW) corrections need to be considered. A first evaluation of the leading weak corrections to dijet production has been presented in [9]. These included the tree-level contributions of $\mathcal{{O}}(\alpha _s\alpha )$ and $\mathcal{{O}}(\alpha ^2)$ and weak loop corrections of $\mathcal{{O}}(\alpha _s^2\alpha )$. Only recently the complete set of NLO corrections, further including QED virtual and real contributions, was completed [10]. While these corrections are rather small for total cross sections, they can reach 10–20% for jet transverse momenta in the TeV range.

A first evaluation of the full set of NLO corrections, of QCD and EW origin, for the three-jet inclusive cross section has been quoted in [11]. In this paper we present results for the fully differential calculation of three-jet production at the LHC to NLO, including all contributions proportional to $\alpha _s^n\alpha ^m$ with $n+m=3$ and $n+m=4$. As a first application we consider the observable $R_{32}$, the ratio of the three-jet and two-jet cross sections, differential in $H_\mathrm {T}^{(2)}$, i.e. the scalar sum of the two leading-jets transverse momenta.

Our paper in organised as follows, in Sect. 2 we present our calculational methods and specify our input parameters. In Sect. 3 we present our results for the full NLO calculation of the three-jet process and the $R_{32}$ observable in particular. We give a summary of our findings in Sect. 4.

2 Setup

To obtain the results presented in Sect. 3 we use the Sherpa Monte-Carlo event generator [12] and interface [13] it to Recola¹ [14, 15]. Therein, the tree-level matrix elements, infrared subtractions, process management and phase-space integration are provided by Sherpa for all contributions to all processes using its tree-level matrix-element generator Amegic [16]. It also implements the infrared subtraction [13, 17,18,19,20,21,22,23,24,25] in the QCD+QED generalisation of the Catani–Seymour scheme [26,27,28,29], including the appropriate initial state mass factorisation counter terms. Recola, on the other hand, using the Collier library [30] for the evaluation of its scalar and tensor integrals, provides the renormalised virtual corrections.

Fig. 1

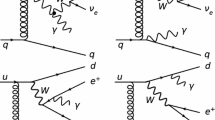
Representative leading and subleading tree-level diagrams for ${{\mathrm {pp}}}\rightarrow 3j$ production. The occurrence of QCD and electroweak interferences, internal electroweak bosons and external photons (wavy lines) in the initial and final state are exemplified. While QCD vertices are marked by a black dot, EW interactions are indicated in red

Fig. 2

Representative leading and subleading virtual correction diagrams for ${\mathrm {pp}}\rightarrow 3j$ production. The occurrence of interferences, QCD and EW loops, gauge boson (wavy line), Higgs boson (dashed line) and top quark (double line) exchange as well as external photons are exemplified. While QCD vertices are marked by a black dot, EW interactions are indicated in red

All calculations are performed in the framework of the Standard Model, assuming a diagonal CKM matrix, and using the five-flavour scheme, i.e. treating the bottom quark as massless. The complex mass scheme [31, 32] is used to consistently treat intermediate resonances in the contributing amplitudes. All electroweak Standard Model parameters are defined in the $G_\mu$-scheme, and virtual amplitudes are renormalised correspondingly. Consequently, the following set of input parameters is used throughout

$$\begin{aligned} \begin{array}{rclrcl} G_\mu &{}=&{} 1.16639\times 10^{-5}\; \text {GeV}^{-2} &{}&{}&{} \\ m_W &{}=&{} 80.385\; \text {GeV} &{} \varGamma _W &{}=&{} 2.085\; \text {GeV} \\ m_Z &{}=&{} 91.1876\; \text {GeV} &{} \varGamma _Z &{}=&{} 2.4952\; \text {GeV} \\ m_h &{}=&{} 125.0\; \text {GeV} &{} \varGamma _h &{}=&{} 0.00407\; \text {GeV}\\ m_t &{}=&{} 173.21\; \text {GeV} &{} \varGamma _t &{}=&{} 1.3394\; \text {GeV}. \end{array} \end{aligned}$$

All other masses and widths are set to zero. In the above,

$$\begin{aligned} \alpha =\left| \frac{\sqrt{2}\;G_\mu \;\mu ^2_W\,\sin ^2\theta _\text {w}}{\pi } \right| , \end{aligned}$$

(1)

defines the electromagnetic coupling. The complex mass of particle i and the weak mixing angle are defined according to

$$\begin{aligned} \mu _i^2=m_i^2-{\mathrm {i}}m_i\varGamma _i \quad \text {and}\quad \sin ^2\theta _\text {w}=1-\frac{\mu _W^2}{\mu _Z^2}, \end{aligned}$$

(2)

respectively.

For the parton density functions we use the NNPDF3.1 NLO PDF set [33] with $\alpha _s(m_Z)=0.118$ and including QED effects (at $\mathscr {O}(\alpha )$, $\mathscr {O}(\alpha _s\alpha )$ and $\mathscr {O}(\alpha ^2)$) in the parton evolution employing the LUXqed scheme [34, 35].² They are interfaced through Lhapdf [36]. The renormalisation and factorisation scales are defined as

$$\begin{aligned} \mu _R=\mu _F=\tfrac{1}{2}\,\hat{H}_\mathrm {T}. \end{aligned}$$

(3)

The variable $\hat{H}_\mathrm {T}$ is thereby given by the scalar sum of all final-state particles’ transverse momenta without applying any jet clustering. To estimate the uncertainty on our computation from uncalculated higher-order contributions, we vary the renormalisation and factorisation scales independently by the customary factor two, keeping $\tfrac{1}{2}\le \mu _R/\mu _F\le 2$. All scale variations were calculated on-the-fly using the event-reweighting algorithm detailed in [37].

3 Results

In this section numerical results for the production of a three-jet final state at next-to-leading order accuracy in proton-proton collisions at a centre-of-mass energy of 13 TeV are presented. We generate the respective matrix elements at all contributing orders for all partonic processes with massless three (Born and virtual corrections) and four body final states (real corrections). As final-state particles we consider five quark flavours and gluons, as well as photons, leptons and neutrinos. Jets are then defined through the anti-$k_t$ algorithm [38] using FastJet [39], with $R=0.4$ as radial parameter. All massless particles of our calculation, except for the neutrinos, are considered as jet constituents. Jets with a net lepton number³ and within $|\eta |<2.5$ are removed from the list of jets. The final state then has to contain at least three surviving jets with $|\eta (j)|<2.8$, of which the leading jet, ordered in transverse momentum, must have $p_\mathrm {T}(j_1)>80\,\text {GeV}$ and all subleading jets $p_\mathrm {T}(j_i)>60\,\text {GeV}$ ($i>1$). This ensures that a jet definition with inherent lepton rejection, which is both infrared-safe at NLO and close to experimental analysis strategies, is used. Nonetheless, it is worth pointing out that lepton final states may survive this lepton-anti-tagged jet definition if either a collinear lepton pair is contained in a single jet (possibly coming from a collinear $\gamma \rightarrow \ell ^+\ell ^-$ splitting), or the jet containing the lepton is outside the rapidity range in which the lepton can be identified. To analyse our results we use the Rivet package [40].

The full NLO n-jet production cross section can be decomposed into contributions of varying power of the strong and electromagnetic coupling. In what follows we employ the convention:

$$\begin{aligned} \sigma _{nj}= & {} \sigma _{nj}^\text {LO}+ \sigma _{nj}^{\varDelta \text {NLO}},\nonumber \\ \sigma _{nj}^\text {LO}= & {} \sum \limits _{i=0}^{n} \sigma ^{\text {LO}_{i}}_{nj},\quad \mathscr {O}\left( \sigma ^{\text {LO}_{i}}_{nj} \right) =\alpha _s^{n-i} \alpha ^{i},\nonumber \\ \sigma _{nj}^{\varDelta \text {NLO}}= & {} \sum \limits _{i=0}^{n+1} \sigma ^{\varDelta \text {NLO}_{i}}_{nj},\quad \mathscr {O}\left( \sigma ^{\varDelta \text {NLO}_{i}}_{nj} \right) =\alpha _s^{n+1-i} \alpha ^{i}, \end{aligned}$$

(4)

such that $\varDelta \text {NLO}_i$ accounts for the virtual and real QCD corrections while $\varDelta \text {NLO}_{i+1}$ accounts for the virtual and real electroweak corrections to $\text {LO}_i$. Representative diagrams for the various tree-level and virtual contributions can be found in Figs. 1 and 2, respectively. It is worth noting that our full NLO calculation in the five-flavour scheme is indeed sensitive to the full Standard Model spectrum, including the top-quark, the Higgs boson and all lepton and neutrino flavours.

Table 1 Full NLO fiducial cross section for two- and three-jet production in the phase space detailed in the text, i.e. $p_\mathrm {T}(j_1)>80\; \text {GeV}$ and $p_\mathrm {T}(j_i)>60\; \text {GeV}$ ($i>1$). Besides the total cross section the relative contributions for the terms specified in Eq. (4) are given

Table 2 As Table 1 but with the additional requirement of $p_\mathrm {T}(j_1)>2\; \text {TeV}$

Table 3 Fiducial cross sections for two- and three-jet production and their corresponding scale uncertainties for a leading-jet selection of $p_\mathrm {T}(j_1)>80\; \text {GeV}$. The respective cross section definitions are given in Eqs. (5) and (6)

Table 4 As Table 3 but with the additional requirement of $p_\mathrm {T}(j_1)>2\; \text {TeV}$

Based on the above decomposition we can furthermore define the pure QCD LO and NLO cross sections as

$$\begin{aligned} \begin{aligned} \sigma _{nj}^{\text {LO}\;\text {QCD}}&=\sigma _{nj}^{\text {LO}_{0}},\\ \sigma _{nj}^{\text {NLO}\;\text {QCD}}&=\sigma _{nj}^{\text {LO}_{0}}+\sigma _{nj}^{\varDelta \text {NLO}_{0}}, \end{aligned} \end{aligned}$$

(5)

respectively. The pure NLO EW corrections and their additive and multiplicative combination with the QCD process are defined as

$$\begin{aligned} \begin{aligned} \sigma _{nj}^{\text {NLO}\;\text {EW}}&=\sigma _{nj}^{\text {LO}_{0}}+\sigma _{nj}^{\varDelta \text {NLO}_{1}}, \phantom {\frac{\sigma _{nj}^{\varDelta \text {NLO}_{0}}}{\sigma _{nj}^{\text {LO}_{0}}}} \\ \sigma _{nj}^{\text {NLO}\;\text {QCD}+\text {EW}}&=\sigma _{nj}^{\text {LO}_{0}}+\sigma _{nj}^{\varDelta \text {NLO}_{0}}+\sigma _{nj}^{\varDelta \text {NLO}_{1}}, \\ \sigma _{nj}^{\text {NLO}\;\text {QCD}\times \text {EW}}&=\sigma _{nj}^{\text {LO}_{0}} \left( 1+\frac{\sigma _{nj}^{\varDelta \text {NLO}_{0}}}{\sigma _{nj}^{\text {LO}_{0}}}\right) \left( 1+\frac{\sigma _{nj}^{\varDelta \text {NLO}_{1}}}{\sigma _{nj}^{\text {LO}_{0}}}\right) . \end{aligned} \end{aligned}$$

(6)

The difference between the additive and multiplicative combination provides an estimate of uncalculated mixed QCD-EW NNLO corrections of $\mathscr {O}(\alpha _s\alpha )$, wrt. LO QCD.

We start our discussion of results by listing the inclusive two- and three-jet cross sections for leading-jet selections of $p_\mathrm {T}(j_1)>80\,\text {GeV}$ and $p_\mathrm {T}(j_1)>2\,\text {TeV}$ in Tables 1 and 2, respectively. We quote results at full NLO accuracy in the Standard Model and list their decomposition into all contributing orders. The numbers quoted in parentheses indicate the statistical error estimate on the last digit given. For a leading jet requirement of $p_\mathrm {T}(j_1)>80\,\text {GeV}$ corrections of EW origin are generally rather small, reaching for the three-jet case at most a relative contribution to the full NLO result of $-0.7\%$ for $\varDelta \text {NLO}_{1}$. The dominant corrections are of QCD nature and account for $+33\%$ and $-48\%$ for two- and three-jet production, respectively.

Requiring $p_\mathrm {T}(j_1)>2\,\text {TeV}$ changes the picture. While for the two-jet process the QCD NLO corrections are still dominating, amounting to $+37\%$, QCD-EW mixed Born and EW one-loop contributions clearly become sizeable, though they largely cancel. For three-jet production in this selection and scale choice the NLO QCD corrections are, accidentally, miniscule, below $-1\%$. However, the Born contributions of EW origin reach a total of $+11\%$ but largely get cancelled by the $\varDelta \text {NLO}_{1}$ terms that contribute $-10\%$ to the total NLO result.

In Tables 3 and 4 we quote two- and three-jet cross sections at full NLO, LO QCD, NLO QCD, NLO EW and $\text {NLO}$ $\text {QCD}+\text {EW}$ for the leading-jet selections of $p_\mathrm {T}(j_1)>80\,\text {GeV}$ and $p_\mathrm {T}(j_1)>2\,\text {TeV}$, respectively. Besides the nominal cross sections we give their scale uncertainty estimates obtained from 7-point variations around the central scale choice $\mu _R\,=\,\mu _F\,=\,\tfrac{1}{2}\,\hat{H}_\mathrm {T}$. A significant reduction in particular of the upward variations wrt. LO QCD is observed for predictions including the $\varDelta \text {NLO}_{0}$ terms. Adding the $\varDelta \text {NLO}_{1}$ corrections, however, has no sizeable effect on the scale uncertainties. Furthermore, no systematic reduction of the scale uncertainties of the full NLO results in comparison to the $\text {NLO}$ $\text {QCD}+\text {EW}$ predictions is observed.

In principle, the addition of a $p_\mathrm {T}>2\,\text {TeV}$ requirement on the leading jet, while leaving the subleading jets at $p_\mathrm {T}>60\,\text {GeV}$ only, introduces a large scale hierarchy to cross section results presented in Tables 2 and 4. In principle, this mandates the inclusion of a resummation of the corresponding potentially large logarithms. However, no perturbative instabilities were encountered in this region and we, thus, consider the results reliable. Similar considerations, of course, also apply to the tails of the distributions shown in the following.

Fig. 3

Leading jet transverse momentum in three-jet production. Left: Theoretical uncertainties at LO, NLO QCD, NLO QCD+EW and full NLO. Right: Decomposition of the full NLO result in its contributions defined in Eq. (4)

Fig. 4

Subleading jet transverse momentum in three-jet production. Left: Theoretical uncertainties at LO, NLO QCD, NLO QCD+EW and full NLO. Right: Decomposition of the full NLO result in its contributions defined in Eq. (4)

Fig. 5

Third jet transverse momentum in three-jet production. Left: Theoretical uncertainties at LO, NLO QCD, NLO QCD+EW and full NLO. Right: Decomposition of the full NLO result in its contributions defined in Eq. (4)

Fig. 6

The $H_\mathrm {T}^{(2)}$distribution in two- and three-jet production at the LHC shown in the left and right panel, respectively. Besides the full NLO prediction the central results and scale uncertainty bands for LO and NLO QCD, NLO $\text {QCD}+\text {EW}$ and NLO $\text {QCD}+\text {EW}$ are shown

Fig. 7

Scalar sum of leading and subleading jet transverse momentum, $H_\mathrm {T}^{(2)}$, in two (top panel) and three (bottom panel) jet production, decomposed into contributions from several ranges of $\eta =|\eta _1-\eta _2|/2$. Shown are the NLO QCD, NLO $\text {QCD}+\text {EW}$ and full NLO result as well as the subleading Born contributions $\text {LO}_{1}$ and $\text {LO}_{2}$

Figures 3, 4 and 5 show the three-jet cross section differential in the transverse momentum of the leading, subleading and third hardest jet, respectively. The left hand side panel details the scale uncertainties and relative magnitudes of the LO QCD, the NLO $\text {QCD}+\text {EW}$, the NLO $\text {QCD}\times \text {EW}$ and the complete NLO (full NLO) result in comparison to the NLO QCD prediction. Similarly, the right hand side panel details the relative contributions from the various LO and NLO contributions to the full NLO result for the central scale choice. Note, while positive sub-contributions are represented by a solid line, negative parts are indicated by a dashed line and their corresponding absolute value is displayed here.

In all three distributions we confirm the substantial shape correction and improvement on the scale uncertainty through the NLO QCD corrections observed in earlier calculations of these quantities [3]. The NLO EW corrections themselves lead to the well-known negative corrections of EW Sudakov-type in the high-transverse momentum regime, reaching $-10\%$ for the leading, $-15\%$ for the second and $-15\%$ for the third hardest jet at $p_\mathrm {T}=2\,\text {TeV}$. The very good agreement of the additive and multiplicative combination of QCD and electroweak corrections indicates a negligible size of the relative $\mathscr {O}(\alpha _s\alpha )$ corrections. The remaining subleading LO and NLO contributions, however, cancel the effect of the next-to-leading order electroweak corrections almost completely. In fact, at $p_\mathrm {T}>2.5\,\text {TeV}$ they grow larger and increase the full NLO result beyond the NLO QCD one. The driving ingredients here are the $\mathscr {O}(\alpha _s^3\alpha )$ $\varDelta \text {NLO}_{1}$ terms, the tree-level interference $\mathscr {O}(\alpha _s^2\alpha )$ ($\text {LO}_{1}$) contributions, followed by the interference at $\mathscr {O}(\alpha _s\alpha ^2)$ ($\text {LO}_{2}$) and their respective EW and QCD corrections at $\mathscr {O}(\alpha _s^2\alpha ^2)$ ($\varDelta \text {NLO}_{2}$). All other contributions to the full NLO result remain marginal. It has to be stressed that this cancellation is accidental and highly observable dependent and cannot be inferred to hold for any other observable, or indeed for the same observable in a different fiducial phase space. Lastly we note, that by the inclusion of NLO EW corrections the uncertainty estimates obtained by QCD scale variations increases wrt. the NLO QCD result, however, still being significantly smaller than for the LO QCD prediction.

Figure 6 now displays the results for the scalar sum of the leading and subleading jet transverse momenta, $H_\mathrm {T}^{(2)}$, in two- and three-jet events. While the latter represents a novel result from our full NLO three-jet calculation, the first is obtained from a dijet computation with identical parameter settings, scale choices and PDFs. Qualitatively, the $H_\mathrm {T}^{(2)}$ distributions exhibit the same features as the leading and subleading jet transverse momentum distributions presented before. While the scale uncertainties are shrunk going from LO to NLO QCD, the electroweak corrections show the expected Sudakov behaviour. The relative electroweak corrections are of nearly the same magnitude for both the two- and the three-jet case. This can be understood from the fact that with $H_\mathrm {T}^{(2)}$ in the TeV region, where the electroweak corrections become sizeable, the additional third jet in the three-jet case is predominantly soft and near the jet threshold. In this limit, higher order QCD and EW corrections should factorise. Further, we note that for both distributions the additive and multiplicative combination of NLO QCD and EW corrections give compatible results. As has been observed before in the jet transverse momenta, including electroweak contributions somewhat increases the uncertainty wrt. NLO QCD.

Upon inclusion of the additional subleading LO and NLO contributions NLO EW effects get cancelled and the full NLO result gets very close to the NLO QCD prediction. Interestingly, this is true both for the two- and three-jet case. However, this cancellation is accidental and highly dependent on the observable and the phase space considered. To illustrate this observation, Fig. 7 shows the same observable, $H_\mathrm {T}^{(2)}$, in different regions of absolute pseudorapidity of the leading two-jet system, i.e. $\eta =|\eta _1-\eta _2|/2$. In the central region, which dominates the inclusive result, the subleading contributions, dominated by $\text {LO}_{1}$ in both the two- and three-jet case, have a large positive effect on the cross section. The more forward $H_\mathrm {T}^{(2)}$ is considered, however, the smaller especially the $\text {LO}_{1}$ terms become and the closer the full NLO result is to the NLO $\text {QCD}+\text {EW}$ one. This was already observed in [9]. In this region, also qualitative differences between the two- and three-jet case are apparent. While the further subleading contributions are negative wrt. the NLO $\text {QCD}+\text {EW}$ result in the dijet case, they are positive wrt. the NLO $\text {QCD}+\text {EW}$ result in the three-jet case.

Fig. 8

The $R_{32}$ observable differential in $H_\mathrm {T}^{(2)}$. Upper panel: Predictions at LO and NLO QCD, NLO $\text {QCD}+\text {EW}$, NLO $\text {QCD}\times \text {EW}$ and full NLO in the Standard Model. Lower panel: Related relative corrections w.r.t. the central NLO QCD result

With full NLO calculations for two- and three-jet production at hand we turn to the central observable of this letter, the three-jet-over-two-jet ratio, $R_{32}$. This particular observable has attracted interest, as large parts of the experimental and theoretical uncertainties in the inclusive three- and two-jet cross sections cancel in the ratio, allowing for a competitive measurement of the strong coupling $\alpha _s$ [41, 42]. Here we consider $R_{32}$ differential in $H_\mathrm {T}^{(2)}$, the scalar sum of the leading- and subleading-jet transverse momenta presented above, i.e.

$$\begin{aligned} \begin{aligned} R_{32}(H_\mathrm {T}^{(2)}) \,=\,\frac{\mathrm {d}\sigma _{3j}/\mathrm {d}H_\mathrm {T}^{(2)}}{\mathrm {d}\sigma _{2j}/\mathrm {d}H_\mathrm {T}^{(2)}}. \end{aligned} \end{aligned}$$

(7)

The scale uncertainties are computed by synchronous variations of numerator and denominator. Our results are presented in Fig. 8.

We find that as the individual input distributions receive only minute EW corrections, resulting in the NLO QCD predictions to agree with the full NLO, also their ratio is very stable. However, as emphasised before, accidental cancellations of individually much larger terms is in action for this observable. Therefore, we present in Fig. 9 results differential in various pseudorapidity regions, with $\eta =|\eta _1-\eta _2|/2$. As before, the inclusive result is dominated by the most central pseudorapidity slices, and they exhibit the same characteristics. In the slightly more forward regions, between $0.5\le \eta \le 2$, the input distributions of Fig. 7 do not exhibit this almost complete cancellation of corrections any longer.

For the cross-section ratio $R_{32}$ the net effect is nonetheless the same and the residual corrections of electroweak and subleading origin are very small. Their contributions largely factorise in the numerator and denominator and, thus, cancel in the ratio. Hence, the full NLO result is in very good agreement with the NLO QCD prediction for this observable. This very much confirms the particular usefulness of $R_{32}$ for the determination of the strong coupling.

Fig. 9

The $R_{32}$ observable at NLO $\text {QCD}+\text {EW}$ and full NLO differential in $H_\mathrm {T}^{(2)}$for different pseudo-rapidity selections and in comparison to the corresponding NLO QCD result

4 Conclusions

In this letter we have presented the evaluation of the full set of Standard Model NLO corrections to three-jet production at the LHC. Besides the dominating QCD corrections of $\mathscr {O}(\alpha _s^4)$ this comprises all (mixed) electroweak tree-level contributions up to $\mathscr {O}(\alpha ^3)$ as well as all (mixed) one-loop and real-corrections up to $\mathscr {O}(\alpha ^4)$. As jet constituents we consider besides quarks and gluons also photons and charged leptons. However, for the considered event selections contributions from final states containing leptons are practically irrelevant. All calculations have been performed in an automated manner within the Sherpa event generation framework, with Recola providing the renormalised virtual corrections.

For the jet transverse momentum distributions and the related $H_\mathrm {T}^{(2)}$ variable we observe a compensation of the electroweak Sudakov-type suppression of high-$p_\mathrm {T}$ events when including subleading electroweak tree-level and one-loop contributions. In fact, for leading jet transverse momenta above $2.5\,\text {TeV}$ a resulting positive correction of $10-15\%$ wrt. the NLO QCD prediction is observed. However, the mentioned compensation is specific for the fiducial phase-space region considered. In particular for jet production away from central rapidity we observe sizeable effects upon inclusion of the full set of (mixed) electroweak corrections. This nicely illustrates the importance of considering the complete set of NLO Standard Model corrections in predictions for the three-jet production process at the LHC.

As a first application of our calculation we have considered the ratio of three- over two-jet production differential in $H_\mathrm {T}^{(2)}$. This variable proves to be very stable against electroweak corrections, confirming its particular usefulness in the determination of the strong coupling constant $\alpha _s$.