1 Introduction

Though we have a well understood QCD Lagrangian, predicting scattering processes involving hadrons is a difficult task. The interaction of a high energy probe with quarks or gluons in a hadron requires us to understand physics which is non-perturbative. While a separation of the perturbative and non-perturbative parts of hadronic processes using factorization exists for processes like deep inelastic scattering, when such simplifications are applied in deriving the scaling laws for exclusive processes [1,2,3,4,5] they are found to be problematic [6]. Theoretical models aimed at explaining exclusive processes have existed for decades now and the ideas can be spilt into two major camps: Methods involving hard gluon exchanges within the constituents (short distance model) and methods without hard exchanges (soft or Feynman mechanism). The Endpoint Model (EP), developed for exclusive hadronic processs at large s and |t|, combines the idea of soft mechanism with a model of hadron wavefunction which constrains the transverse momenta of confined quarks. In [7, 8], the Endpoint model was developed and used to obtain the scaling laws for Dirac and Pauli form factor of the proton (for \(Q^2 > 5.5\,\mathrm{GeV}^2\)) and pp scattering. These successes motivated the author to search for other proton exclusive processes which could be studied using the Endpoint Model.

Pioneering measurements for Compton scattering were made at Cornell [9], where the differential cross section \(d\sigma /dt\) was measured and found to show a scaling of \(1/s^6\) (s, t are the Mandelstam variables). However more recent measurements at JLab [10] have shown that the scaling goes more like \(1/s^{8.0 \pm 0.2}\) where \(s \in [5,11] \, \mathrm{GeV}^2\). Early theoretical predictions for the scaling behaviour of Compton scattering appeared in [11, 12]. They predicted that \( d\sigma /dt|_{\mathrm {fixed\, t}} \propto 1/s^{6} f(t/s)\) using simple constituent counting ideas. Recent calculations in perturbative QCD (short distance model) [13, 14] give predictions smaller than the experimental data. However, it is understood that the perturbative calculations are at best applicable only at asymptotically high momentum transfers not achievable in existing experimental facilities. A soft mechanism was used in [15, 16] in calculations involving generalized parton distribution functions (GPD), while Miller [17] calculated the handbag diagram in the constituent quark model (CQM). While the GPD based analysis agrees with some features of the data, the scaling behaviour is not consistent with the latest data. The former work was shown to be equivalent to a sum of overlap of light cone wave functions for all Fock states. For the leading Fock state, the pole structure leads to a endpoint dominance similar to our model. Recent work by Kivel and Vanderhaeghen [18, 19] on Compton scattering combined the short distance and the soft mechanism using Soft collinear effective theory.

In recent years, the experiments using polarization transfer [20, 21] have also given measurements of transverse polarization transfer \(K_{LS}\) and longitudinal polarization transfer \(K_{LL}\). The latest results on polarization transfer measurements [21] show that, while the \(K_{LS}\) agrees well with the results of pQCD[14], GPD’s [22], CQM [17] and SCET [19], the \(K_{LL}\) measurements have been unexpectedly larger and do not agree with any of the theoretical predictions. Further work will be required to extract these observables in the Endpoint Model.

Fig. 1
figure 1

Two diagrams from Compton scattering of proton in the Endpoint Model

Full size image

1.1 Endpoint Model for hadronic processes

The idea of an endpoint dominated contribution to the exclusive processes was introduced in the papers [23,24,25]. However, the program of using perturbative QCD techniques in exclusive processes overshadowed these ideas till they were reconsidered in [7]. The Endpoint model was the result of an attempt to understand the scaling laws of the pion form factor by assuming that the dominant contribution to the processes comes from the region where one quark carries most of the pion’s momenta. The framework relates the \(x_i\) (momentum fraction of struck quark) dependence of the hadron wavefunction in the endpoint region to the scaling behaviour \(F_{\pi } \sim 1/Q^2\). This allows one to obtain the \(x_i\) dependence of the wavefunction and apply it in the EP calculations of other processes involving the hadron. Specifically for the proton, the study of the Dirac form factor in the Endpoint model [7] led to a model of the wavefunction of the proton. This was then used in [8] to understand the experimentally observed ratio of Pauli and Dirac form factors \(F_2(Q^2)/F_1(Q^2) \sim 1/Q\). Considering hadrons states with soft non-valence partons, in EP calculations of exclusive processes, lead to an additional integration over its momentum fraction \(x_i\in (0,\Lambda / Q)\) causing the contributions to be suppressed by 1 / Q [7].

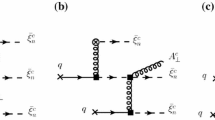
The basic assumption when studying Compton scattering (\(\gamma p \rightarrow \gamma p\)) in the framework of EP is that the dominant contribution comes from the process in which each quark in the end point region absorbs a real photon and then emits it while the remaining quarks act as spectators as shown in Fig. 1. This allows us to proceed along the lines of the calculation in [7] for the proton form factors. Introducing the light cone wavefunction with constrained transverse momenta leads to a dominant contribution from the endpoint region of \(x_{i}\). Carrying out this endpoint dominated calculation for Compton scattering, we will see in Sect. 2 that \(d\sigma / dt\) obeys scaling laws of [11, 12] at large s in the \(s \sim |t| \gg \Lambda _{QCD}\) limit and also the experimentally observed scaling of \(1/t^4\) in the fixed s much larger than |t| region. Detailed numerical calculations in Sect. 3 help us determine the range of s, |t| where the scaling behaviour, for the case \(s \sim |t| \gg \Lambda _{QCD}\), will be valid. We will also extend the model’s prediction into a lower \(Q^2\) region to compare with data. While short distance contributions may dominate at asymptotic energies, the thrust of our analysis is that the Endpoint model can be used to understand data which lies within experimental reach.

2 Compton scattering using the Endpoint Model

The diagrams for Compton scattering in the Endpoint Model are given in Fig. 1, as explained above the photons interact only with the struck quark. It can be noticed that the interaction between the struck quark and the photon mirrors the diagrams of the Compton scattering with electrons.

2.1 Kinematics

In the diagrams shown, the incoming proton can be taken to be deflected by spacelike momentum transfer \(q^{\mu } = (0,Q,0,0)\), where \(q^{\mu } = q_{1}^{\mu } - q_{2}^{\mu }\). This allows us to use the same frame and kinematics for the proton, as was used for the analysis of Dirac and Pauli form factors [7, 8] with initial and final proton momentum \( P=(\sqrt{Q^{2}/2+M_{P}^{2}},-Q/2,0,Q/2), P'=(\sqrt{Q^{2}/2+M_{P}^{2}},Q/2,0,Q/2)\). We can choose \(q_1,q_2\) appropriately so that \(\theta _{cm} \in [64^{\circ }, 130^{\circ }]\), which is the range of the data obtained at Jlab [10]. For \(\theta _{cm} \approx 90^{\circ }\), using momentum conservation and the onshell photon condition, we can obtain \(q_1=\left( Q/\sqrt{2},Q/2,0,-Q/2\right) , q_2=\left( Q/\sqrt{2},-Q/2,0,-Q/2\right) .\)

To describe the various quark momenta, we define a basis for transverse momenta: \( \hat{y}^{\mu } =(0, 0, 1,0) = \hat{y}^{'\mu }\) such that \( \hat{P}\cdot \hat{y}=\hat{P}'\cdot \hat{y}'=0\) and \(\hat{n}^{\mu } = (1/\sqrt{2}) (0, -1, 0, -1)\) such that \( \hat{P}\cdot \hat{n}= 0\) and \(\hat{n}'^{\mu } = (1/\sqrt{2}) (0, 1, 0,-1)\) such that \(\hat{P}'\cdot \hat{n}'=0.\) Here \(\hat{P} = \left( 0,-1/\sqrt{2},0,1/\sqrt{2}\right) \) and \(\hat{P}' = \left( 0,1/\sqrt{2},0,1/\sqrt{2}\right) \) are the unit vectors along the direction of propagation of the incoming photon and incoming proton respectively. The four momenta of the quarks are then given by,

$$\begin{aligned} k_{i}^{\mu }&=\left( k_{i}^{0},-x_{i}\frac{Q}{2}-\frac{k_{in}}{\sqrt{2}},k_{iy},x_{i}\frac{Q}{2}-\frac{k_{in}}{\sqrt{2}}\right) \nonumber \\ k_{i}^{'\mu }&=\left( k_{i}^{'0},x'_{i}\frac{Q}{2}+\frac{k'_{in}}{\sqrt{2}},k'_{iy},x'_{i}\frac{Q}{2}-\frac{k'_{in}}{\sqrt{2}}\right) . \end{aligned}$$
(1)

2.2 Endpoint model calculation

The amplitude for the process can be written as

$$\begin{aligned}&{i}\mathcal {M} = \int \prod \limits _{i} \frac{d^4 k_i}{(2\pi )^4}\frac{d^4 k'_i}{(2\pi )^4} \nonumber \\&\quad \times (2\pi )^4\delta (k_1+k_2+k_3-P) (2\pi )^4\delta (k'_1+k'_2+k'_3-P') \nonumber \\&\quad \times \epsilon ^{*\mu }(q_{2})\epsilon ^{\nu }(q_{1})\left[ \overline{\Psi '}_{\alpha '\beta '\gamma '}(k^{'}_{i}) \times \mathcal {M}_{\alpha '\beta '\gamma '\alpha \beta \gamma }^{\mu \nu }\times \Psi _{\alpha \beta \gamma }(k_{i}) \right] , \end{aligned}$$
(2)

where \(\Psi _{\alpha \beta \gamma }\) is the 3 quark Bethe–Salpeter wavefunction, where indices \(\alpha ,\beta ,\gamma \) refer to the u, u, d carrying momentum \(k_1,k_2,k_3\) respectively. The primed quantities refer to the outgoing proton.

The \(\mathcal {M}^{\mu \nu }\) in the above expression is taken as,

(3)

where we have taken into account both diagrams in Fig. [1] and the three terms represent the photon’s interactions with u,u,d quarks respectively.

In order to replace the Bethe Salpter wavefunctions by Light cone wavefunctions using the approximations developed in [26], we need to integrate over the \(k_i^-, k_i^{'-}\) momenta in the Eq. 2 (where \(k^-\) represents the − component of the light cone momenta). We note that in our case the integrand has \(k_i^-, k_i^{'-}\) dependence due to the propagators associated with the Bethe Salpeter wavefunction and from the spectator quarks. The spectator quarks interact through soft gluons and can be modelled as an effective diquark propagator. In order to model this system one has to do an detailed analysis of the physics in this non-perturbative system. As a simple approximation, we could assume an overlap model in which the spectator quarks propagate as free particles of effective mass m. With this model, the complete expression for \(\mathcal {M}^{\mu \nu }\) is assumed to be dominated by a region where the quarks are on-shell which allows us to make the substitution \(\kappa _i^- = (k^0 - x_i Q/\sqrt{2})(P^0+Q/\sqrt{2})= (m_i^2+\mathbf {k}^2_{\perp \, i})(P^0+Q/\sqrt{2})/(k^{0} + x_i Q/\sqrt{2})\). This substitution, takes into account the energy scale dependence of the quark mass which causes the effective mass to be \(m^2_i\sim \Lambda ^2\) for the spectator quarks and \(m^2_i \sim \) few MeV for the struck quark. The above spectator model is only a simple approximation and, in future, it will be useful to explore a more general structure for the diquark propagator.

After these steps, the amplitude Eq. 2 becomes

$$\begin{aligned}&{i}\mathcal {M} = \int \prod \limits _{i} dx_{i}d\mathbf {k}_{\perp i} dx^{'}_{i}d\mathbf {k}'_{\perp i} \delta (x_{1}+x_{2}+x_{3}-1)\delta ^{2}\nonumber \\&\quad \times (k_{\perp 1}+k_{\perp 2}+k_{\perp 3})\delta (x'_{1}+x'_{2}+x'_{3}-1)\nonumber \\&\quad \times \delta ^{2}(k'_{\perp 1}+k'_{\perp 2}+k'_{\perp 3})\epsilon ^{*\mu }(q_{2})\epsilon ^{\nu }(q_{1})\nonumber \\&\quad \left[ \overline{Y^{\prime }}_{\alpha ^{'}\beta ^{'}\gamma ^{'}}(x'_{i},\mathbf {k}'_{\perp i})\times \mathcal {M}_{\alpha '\beta '\gamma '\alpha \beta \gamma }^{\mu \nu }\times Y_{\alpha \beta \gamma }(x_{i},\mathbf {k}_{\perp i})\right] . \end{aligned}$$
(4)

The light cone wave function for the proton \(Y(k_i)\) at leading power of large P is modelled as [27,28,29,30,31],

(5)

Here \(\mathcal {V,A,T}\) are scalar wavefunctions of the quark momenta, N is the proton spinor, \(N_{c}\) the number of colors, C the charge conjugation operator, \(\sigma _{\mu \nu }= \frac{{i}}{2}[\gamma _{\mu },\gamma _{\nu }]\), and \(f_{N}\) is a normalization. The simplest form of the wavefunction has been chosen for our analysis, additional terms which involve sub-leading momenta could be added to the above wavefunction but are not expected to change the scaling behaviour of the cross section. Note that the x dependence of the wave function is chosen in order to reproduce the scaling behaviour of the hadron form factor. Hence each of these additional terms will either contribute to the dominant term in the form factor which survives in the large \(Q^2\) limit or give a subdominant contribution. Once such a choice is made, we believe that it will necessarily lead to the correct scaling behaviour of all exclusive processes including Compton scattering [7]. A calculation with a general form for the Dirac structure of the wavefunction may be pursued in future work. As discussed in [7], the scalar wave functions \(\mathcal {V,A,T} \) are constructed by first assuming an exponential ansatz \( \sim \phi (x_i) exp(-\mathbf {k}^2_{T}/\Lambda _{QCD}^2)\). The exponential dependence represents our understanding that the transverse momenta \(\mathbf {k}_T\) of the quark is understood to be cut off sharply for \(|\mathbf {k}_T| > \Lambda _{QCD}\). Due to the form of \(k_{in}\) after momentum conservation, as derived below, we obtain a integral dominated by the endpoint region of the \(x_i\). The x-dependence of the wavefunction in this region was extracted from data in [7] where EP was applied to the problem of the Dirac form factor. This leads to the following form of the scalar functions

$$\begin{aligned}&\mathcal {V} = v (1-x_i)\mathrm {e}^{- k_{T}^{2}/\Lambda ^{2}};\quad \mathcal {A} = a (1-x_i)\mathrm {e}^{- k_{T}^{2}/\Lambda ^{2}};\quad \nonumber \\&\quad \mathcal {T} = t (1-x_i)\mathrm {e}^{- k_{T}^{2}/\Lambda ^{2}} , \end{aligned}$$
(6)

where v, a, t are the normalization constants

2.3 Scaling in Endpoint Model

Before presenting the Endpoint Model’s prediction for Compton scattering, we analytically evaluate a part of the entire expression to extract the scaling behaviour to be expected for fixed \(\theta _{CM}\) and fixed s cases.

Let us concentrate on the diagram shown in Fig. 1, in which d quark is struck. The delta functions in the last term of Eqs. 3 and 4 imply, \( x_{1} = 1 - x_{2} - x_{3}; x'_{1} = 1 - x'_{2} - x'_{3}; k_{1n} = -k_{2n} - k_{3n}; k_{1y} = -k_{2y} - k_{3y} ; k'_{1n} = -k'_{2n} - k'_{3n}; k'_{1y} = -k'_{2y} - k'_{3y} ; k_{2y} = k'_{2y}; k_{3y} = k'_{3y} ;\, x'_{2}= x_{2}; x'_{3}= x_{3}; k_{3n}=Q(1-x'_{3})/\sqrt{2} ;\, k'_{3n}=Q(1-x_{3})/\sqrt{2}; k_{2n}=Q(-x'_{2})/\sqrt{2} ;\, k'_{2n}= Q(-x_{2})/\sqrt{2}. \) Integrating over the delta functions also leads to a factor of \(1/Q^2\).

Using only the first term of the wavefunction Eq. 5, the amplitude is obtained as,

(7)

The experimentally measured quantity is the unpolarized differential cross section \(d\sigma /dt= 1/16\pi (s-m_p^2)^2 1/4\sum |M|^2\),

(8)

We can integrate over the variables after plugging in the wavefunction from Eq. 6. This step changes the limits of integration making the contribution endpoint dominant: \(x_1, x_2\in (0,\Lambda / Q)\). Our calculation shows scaling behaviour in two limits, for \(s \sim |t| \gg \Lambda _{QCD}\) and for fixed s much larger than |t|. In the \(s \sim |t| \gg \Lambda _{QCD}\) limit, the scaling can be extracted from Eq. 8 by picking out the leading order contributions from the traces and the denominators combined with the integration of the x-dependence of the wavefunction in the endpoint region. For example, considering the following traces from the Eq. 8,

(9)

we obtain

$$\begin{aligned}&\frac{d\sigma }{dt} \sim \int dx_1 dx_2 dk_{1y} dk_{2y} \int d\widetilde{x}_1 d\widetilde{x}_2 d\widetilde{k}_{1y} d\widetilde{k}_{2y} \frac{1}{16\pi (s-m_p^2)^2}\nonumber \\&\quad \left( \frac{1}{Q^2}\right) ^2\left( 4 m_1 m_2 (P\cdot P')+\dots \right) \nonumber \\&\quad \times \left( 4 m_1 m_2 (P\cdot P')+\dots \right) \frac{\left( 16(k_3\cdot P)(\widetilde{k}_{3}\cdot P')+\dots \right) }{(k_3\cdot q_1)(\widetilde{k}_3 \cdot q_1)}\nonumber \\&\quad (1-x_3)^2 (1-\widetilde{x}_{3})^2 + \cdots \nonumber \\&\quad \sim \frac{1}{s^2}\left( \frac{1}{Q^2}\right) ^2(Q^2)^2\frac{(Q^2)^2}{(Q^2)^2}\frac{1}{Q^4}\frac{1}{Q^4}\sim \frac{1}{s^2}\times \frac{1}{s^2}\times \frac{1}{s^2} \sim \frac{1}{s^6}. \end{aligned}$$
(10)

Thus in the large s limit, we can see that we obtain a scaling behavior of \(1/s^6\), as expected from the quark counting rules.

To analyse the differential cross section for fixed s when \(s>> t\), we must alter the photon momenta defined specifically for \(\theta _{CM} = 90^{\circ }\) above and instead use \( q_1=\left( Q/\sqrt{2}, Q/2,0,f(s,Q)\right) \), \( q_2=\left( Q/\sqrt{2},-Q/2,0,f(s,\right. \left. Q)\right) \). The definition of \(s = (P+q_1)^2\) can be used to find the functional form of f(s, Q). To the leading order in s, it can be shown that \(f(s,Q) \sim \pm s/Q\). In the \(s>> t \) limit, the leading order contributions are now,

$$\begin{aligned}&\frac{d\sigma }{dt} \sim \int dx_1 dx_2 dk_{1y} dk_{2y} \int d\widetilde{x}_1 d\widetilde{x}_2 d\widetilde{k}_{1y} d\widetilde{k}_{2y} \frac{1}{16\pi (s-m_p^2)^2}\nonumber \\&\quad \left( \frac{1}{Q^2}\right) ^2(4 m_1 m_2(P\cdot P')+\dots )\nonumber \\&\quad \times (4 m_1 m_2 (P\cdot P')+\dots ) \frac{(16(q_1\cdot P)(q_1\cdot P')+\dots )}{(k_3\cdot q_1)(\widetilde{k}_3 \cdot q_1)}\nonumber \\&\quad (1-x_3)^2 (1-\widetilde{x}_{3})^2 + \cdots \nonumber \\&\quad \sim \frac{1}{s^2}\left( \frac{1}{Q^2}\right) ^2(Q^2)^2\frac{s^2}{s^2}\frac{1}{Q^4}\frac{1}{Q^4} \sim \frac{1}{Q^4}\times \frac{1}{Q^4} \sim \frac{1}{Q^8} \sim \frac{1}{t^4} \end{aligned}$$
(11)

The scaling observed in the above cases depends on the endpoint nature of the dominant contribution. A change in the model for the spectator quark system may change the magnitude of the result, however the scaling behaviour observed in this section will remain unchanged.

3 Comparing Compton scattering in Endpoint Model with experimental data

In order to obtain the numerical prediction for Compton scattering, we first need to fix the parameters of the Endpoint model. Previous work on EP [7] obtained a specific model for the \(x_{i}\) dependence of the wavefunction using the scaling behaviour of exclusive processes. Here, we extend the above work by using \(\chi ^2\) minimization to extract the free parameters of the model: the constants in the wavefunction v, a, t.

We do a \(\chi ^2\) minimization using the expressions for \(F_1\) and \(F_2\) developed in [8], based on the above model, and the data for \(F_1\)[32] and \(F_2/F_1\)[33, 34](at \(Q^2 \gtrsim 5.5 \,\mathrm{GeV}^2\)). With this exercise we are able to achieve, not only a agreement with the scaling behaviour of the proton form factors but also an agreement with the magnitudes of the experimental observations for \(Q^2 \gtrsim 5.5 \,\mathrm{GeV}^2\). The minimization gives us a range of v, a, t for different values of the spectator mass \(m_i\), which we will use in obtaining a fit with the magnitude of the Compton scattering data.

Fig. 2
figure 2

Plot of \(d\sigma / dt\) nbarns/GeV\(^2\) vs t for s = 6.79, 8.90, 10.92 GeV\(^2\) and m=0.11  GeV; v = 41.25, a = 0, t = 38.26 (\(\mathrm{GeV}^{-2}\))

Full size image

The prediction of the Endpoint Model for Compton scattering comes from combining the full expressions Eqs.  3, 5 in  8. It is easy to see that the expression will become cumbersome due to the traces over multiple gamma matrices and can be handled by using the Mathematica package FEYNCALC [35]. The resulting expression contains many terms for each combination of wavefunction \(\mathcal {V,A,T}\) making an analytic evaluation difficult. The integration is then done using a Monte Carlo routine for integration (VEGAS [36]) to obtain a numerical prediction for Compton scattering. The only input to these calculations are the co-efficients of the wave function v, a, t from the \(\chi ^2\) analysis described above. In our analysis, we observed that for a range of masses, the fitting to the form factor data does not change significantly allowing us the freedom to use the mass as a parameter to obtain an agreement with the data of Compton scattering. We observe that the choice of mass \( m = 0.11 \, \mathrm{GeV}\) and corresponding wavefunction co-efficients : \(v = 41.24, a = 0, t = 38.26 \) (\(\mathrm{GeV}^{-2}\)) give an agreeable fit as seen the Figs. 2, 3 below. These constants should now carry over to all the processes that EP may be applied to. The numerical results for the two regimes of s, t that we study show that:

Fig. 3
figure 3

EP evaluation of \(d\sigma /dt\) \(\mathrm {nbarns}/\mathrm{GeV}^2\) vs s \(\hbox {GeV}^2\) for m = 0.11 GeV; v = 41.25, a = 0, t = 38.26 (\(\mathrm{GeV}^{-2}\))

Full size image
  1. (i)

    For fixed s, experiments were done for s = 6.79, 8.90, 10.92 \(\,\mathrm{GeV}^2\) and we observe that the data shows a scaling behaviour of \(1/t^4\) for |t| much smaller than s. We carry out EP calculations for the above values of s and find good agreement with data. The scaling is correctly reproduced by the complete numerical calculation as was also seen in the analytic calculation in Sect. 2.3, valid at large values of s and |t|. We can see in Fig. 2 that there is a good agreement between the data and our EP prediction at the above energies, which improves as we increase the s of the data. As seen in Fig. 2 for \(s=8.90 \,\mathrm{GeV}^2\) and \(Q^2 \gtrsim 3.5 \,\mathrm{GeV}^2\), the EP model at fixed s does not correctly predict rise in the \(d\sigma / dt\). The angular dependence suggests that a different subprocess becomes important at larger angles. We also observe that for large angles the predictions of the Endpoint model become vulnerable to a singularity from the u channel propagator. This could have interesting implications on the form of the interaction kernel that we plan on exploring in further detail in future work.

  2. (ii)

    Experimentally, cross section was measured at values of \(\theta _{CM} \in [64^{\circ }, 130^{\circ }]\) and it was observed that the cross section scales as \(1/s^8\). We do a numerical calculation for \(d\sigma /dt\) in the \(s \sim t\) limit at \(\theta _{CM}=90 ^{\circ }\) for a wide range of s. As is obtained analytically in Sect. 2.3, we expect that at sufficiently high energies \(d\sigma /dt \propto 1/s^6\) in agreement with the constituent counting rules. Our numerical calculation shows that this behaviour sets in only for \(s>25 \,\mathrm{GeV}^2\). This energy scale has so far not be explored experimentally. At lower values of s, we find that the cross section falls much faster and shows good agreement with the experimentally observed scaling of \(1/s^8\). The predicted magnitude of the cross section also shows good agreement with data. Future experiments at higher energies will allow us to verify our predicted value of s at which the asymptotic scaling behaviour sets in.

4 Conclusions

The Endpoint model combines the soft mechanism and the nature of transverse momenta of a quark in a hadron to predict scaling behaviour in its exclusive processes. Using the model to calculate exclusive processes leads to expressions dominated by the endpoint region of the wavefunction, this helps us extract the form of the wavefunction. For the proton, using \(F_1\) data to obtain the wavefunction, the scaling behaviour of the form factor ratio \(F_2/F_1\) of proton as well as pp scattering were successfully predicted. The successes of the Endpoint model lead us to investigate the problem of real Compton scattering of the proton.

The experimental data for Compton scattering [10] show a scaling behaviour for the differential scattering cross section in two regions of s, t: a \(1/s^8\) scaling for fixed \(\theta _{CM}\) and \(s \sim |t| \gg \Lambda _{QCD}\) and a \(1/t^4\) scaling at fixed s much larger than |t|. Fixing the free parameters in the Endpoint Model at mass \( m = 0.11 \, \mathrm{GeV}^2\) using the data for \(F_1\) and \(F_2/F_1\), we carried out numerical calculation for Compton scattering in these limits. For fixed s larger than |t|, the Endpoint calculations show the \(1/t^4\) scaling observed in data and has a good match with the data for smaller angles. In the fixed \(\theta _{CM}\) and \(s \sim |t| \gg \Lambda _{QCD}\) region, the Endpoint Model calculation for the Compton scattering shows the elusive \(1/s^6\) scaling, that is expected from constituent counting rules [11, 12]. Moreover, the Endpoint model also suggests that the \(1/s^6\) scaling can be expected to be dominant only for \(s \gtrsim 25 \, \mathrm{GeV}^2\). This paper provides a first prediction of the energy scale for the onset of this scaling regime. At the experimental values of s, a good agreement with experimental observations can be seen when extending the calculation to lower s (lower  \(Q^2\)).

With the current work, we have shown once again that the Endpoint model is capable of explaining a range of scaling laws for exclusive hadronic processes at high s and |t|. It is capable of generating the quark counting rules [11, 12] and also suggests the energy scales at which one can expect these scaling laws to dominate for Compton Scattering. Fixing the parameters of the model using existing data, the Endpoint model is also able to give an good match with experimental data over a broad regime.