1 Introduction

The chiral and gauge symmetry breaking in quantum field theories can be promoted by fundamental scalar bosons through the Higgs boson mechanism. If this particle is a composite or an elementary scalar boson is still an open question. Many models have considered the possibility of a light composite Higgs based on effective Higgs potentials as reviewed in Ref. [1]. Nambu and Jona-Lasinio proposed one of the first field theoretical models based on the ideas of superconductivity, where all the most important aspects of chiral symmetry breaking and mass generation, as known nowadays, were explored at length [2]. The model of Ref. [2] contains only fermions possessing invariance under chiral symmetry, although this invariance is not respected by the vacuum of the theory and the fermions acquire a dynamically generated mass. As a consequence of the chiral symmetry breaking by the vacuum the analysis of the Bethe–Salpeter equation (BSE) shows the presence of Goldstone bosons. These bosons, when the theory is assumed to be the effective theory of strongly interacting hadrons, are associated to the pions. Besides these aspects Nambu and Jona-Lasinio also verified that the theory presents a scalar bound state (the sigma meson), which plays the role of the Higgs boson in their strong interaction model.

In Quantum Chromodynamics (QCD) the same mechanism is observed, where the quarks acquire a dynamically generated mass (\(\mu \)). This dynamical mass is usually expected to appear as a solution of the SDE for the fermion propagator when the coupling constant is above a certain critical value. The same condition that leads to chiral symmetry breaking is also responsible to generate a bound-state massless pion, and a scalar p-wave state of the BSE, indicating the presence of a scalar state with mass \(m_\sigma = 2 \mu \). This scalar meson is the elusive sigma meson [4,5,6], that is assumed to be the Higgs boson of QCD. This scenario is the accomplishment of Nambu and Jona-Lasinio proposal in the context of renormalizable gauge theories.

The possibility of spontaneous gauge and chiral symmetry breaking promoted by a composite scalar boson in the context of the Standard Model (SM) was formulated in the seventies by Weinberg [7] and Susskind [8]. The most popular version of these models was dubbed as technicolor (TC), where new fermions (or technifermions) condensate and may be responsible for the chiral and SM gauge symmetry breaking [9,10,11,12,13]. However the phenomenology of these models depend crucially on these new fermions (or technifermions) self-energy. In the early models this self-energy was considered to be given by the result [14, 15]

$$\begin{aligned} \varSigma _{TC} (p^2) \propto \frac{\left\langle {{\bar{T}}_f}T_f\right\rangle _{\mu }}{p^2}, \end{aligned}$$
(1)

where \(\left\langle {{\bar{T}}_f}T_f\right\rangle _\mu \sim \mu ^3\) is the TC condensate and \(\mu \) is the characteristic TC dynamical mass scale, which is of order of a few hundred GeV, i.e. the order of the SM vacuum expectation value. Unfortunately early technicolor models suffered from problems like flavor changing neutral currents (FCNC) and contributions to the electroweak corrections not compatible with the experimental data [9, 11,12,13]. These problems occur when new extended technicolor interactions (ETC) are introduced in order to provide masses to the standard quarks. Equation (1) leads to quark masses that vary with the ETC mass scale (\(M_E\)) as \(1/M_E^2\).

A possible way out of this dilemma was proposed by Holdom [16] many years ago, remembering that the self-energy behaves as

$$\begin{aligned} \varSigma _{TC} (p^2)\approx \frac{\left\langle {{\bar{T}}_f}T_f\right\rangle _{\mu }}{p^2} \left( \frac{p}{\mu }\right) ^{\gamma _m} \,\, \end{aligned}$$
(2)

where \(\gamma _m\) is the mass anomalous dimension associated to the fermionic condensate. As can be verified from Eq. (2) a large anomalous dimension leads to a hard asymptotic self-energy (or quasi-conformal technicolor theories) and this may solve the many problems of the SM symmetry breaking promoted by composite bosons [17,18,19,20,21,22,23,24]. Quark masses will be less dependent on the ETC interactions in the case of a hard TC self-energy, leading to a less problematic phenomenology.

There are different ways of obtaining a large \(\gamma _m\) value in Eq. (2), in what is known as extreme walking (or quasi-conformal) TC theories. (1) It is possible to obtain an almost conformal TC theory when the fermions are in the fundamental representation introducing a large number of TC fermions (\(n_{TF}\)), leading to an almost zero \(\beta \) function and flat asymptotic coupling constant. The cost of such procedure may be a large S parameter [25, 26], such behavior can also be obtained when the fermions are in larger representations other than the fundamental one [27,28,29]; or (2) by inclusion of four-fermion interactions [30,31,32,33,34,35]. We should note that in the last years there has been an increased application of lattice gauge theory to models other than QCD, particularly to field theories that may find application in describing physics beyond the SM [36,37,38]. Considering applications to TC models, in Ref. [39] the authors consider QCD with 2 colour-sextet quarks as a possible walking-Technicolor candidate and the discussion presented in this work and, in particular, the one of Ref. [40] is fully compatible with the lattice results, because any change of the fermionic content and respective Casimir eigenvalues will also modify the SDE boundary conditions leading to a slower decrease of the TC self-energy with the momenta.

Most of these studies were performed looking at SDE solutions of the technifermion propagator. In particular, after a work by Takeuchi [41], it became clear that the technifermion self-energy may vary between the behavior of Eq. (1) and the extreme behavior, that in the past was called irregular solution [14], that is giving by

$$\begin{aligned} \varSigma _{TC} (p^2)\approx \mu \left[ 1 + bg^2 (\mu ^2) \ln \left( p^2/\mu ^2 \right) \right] ^{-\delta }, \end{aligned}$$
(3)

where in Eq. (3) g is the TC running coupling constant, b is the coefficient of \(g^3\) term in the renormalization group \(\beta (g)\) function, \(\delta = \frac{3c}{16\pi ^2 b}\) , and c is the quadratic Casimir operator given by

$$\begin{aligned} c = \frac{1}{2}\left[ C_{2}(R_{1}) + C_{2}(R_{2}) - C_{2}(R_{3})\right] , \end{aligned}$$

and \(C_{2}(R_{i})\), are the Casimir operators for fermions in the representations \(R_{1}\) and \(R_{2}\) that form a composite boson in the representation \(R_{3}\). The behavior of Eq. (3) happens when the theory is totally dominated by a four-fermion interaction, like in the Nambu–Jona-Lasinio model, and it is quite interesting because it may lead to a composite TC scalar boson much lighter than the TC characteristic scale [42,43,44,45,46]. Equation (3) leads to quark masses that vary with the ETC mass scale as \([\ln (\mu ^2/M_E^2)]^{-\delta }\).

It is important to remark that the behavior of Eq. (3) was obtained by Takeuchi[34] with the “ad hoc” addition of an effective four-fermion interaction. Here we shall show that this hypothesis is not necessary. Inverting the diagram that gives mass to ordinary fermions (see Fig. 1b2), we obtain a diagram (Fig. 1a2) that gives a tiny mass to technifermions, changing the TC self-energy to the form of Eq. (3), and this happens only as a function of QCD parameters. The coupled SDE system that we shall discuss is at the origin of the hard self-energies, without appealing to any new effect (like an arbitrary four-fermion interaction, a large number of fermions or a non-trivial fixed point).

It is not surprising that the introduction of a four-fermion interaction may change the ultraviolet SDE behavior. As observed by Cohen and Georgi [47] much of the information about chiral symmetry breaking resides into the boundary conditions, and the introduction of new interactions change these conditions. Recently we discussed how the boundary conditions of the anharmonic oscillator representation of the SDE for SU(N) gauge theories are directly related to, and may change, the mass anomalous dimensions [48]. Motivated by this we studied how the introduction of radiative corrections into the SDE may change the self-energy solutions [40], and verified that when TC is embedded into a larger theory including also QCD, radiative corrections couple the different strongly interacting Dyson equations (TC and QCD) and change completely the ultraviolet behavior of the gap equation solution. The work of Ref. [40] was performed numerically and we just commented, without presenting the details of the calculation, that the effect of the radiative corrections in the coupled equations was similar to a change in the anomalous mass dimension of the theory. The purpose of this work is to show in detail how the coupled TC and QCD have their boundary conditions changed by the ETC radiative corrections, in such a way that the self-energies ultraviolet behavior turn out to be of the form that we may call extreme walking or irregular one, i.e. the behavior of Eq. (3), what may indicate a new way to build TC models as described in Ref. [40].

This work is organized as follows, in Sect. 2 we present the TC and QCD coupled SDE system discussed in Ref. [40], we transform the integral SDE equations into a pair of differential equations, and considering some approximate analytical expressions we recover the numerical result of Ref. [40], where the quark mass is totally dominated by the irregular solution given by Eq. (3), and in Sect. 3 we verify how the boundary conditions of the gap equations are changed and are, consequently, responsible by the different asymptotic self-energies behavior. In Sect. 4 we draw our conclusions.

Fig. 1
figure 1

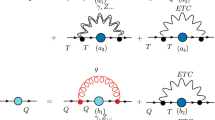
The Schwinger–Dyson equations [40] for QCD (q\(\,\equiv \,\)quark) and TC (Q\(\,\equiv \,\)technifermion) including ETC and electroweak or other corrections (\(\gamma ,Z\ldots \)). In the above figure \(G \,(g)\) indicate technigluons (gluons) propagators

Full size image

2 TC and QCD coupled SDE system by ETC interactions

In Ref. [40] we discussed a coupled SDE system where two strongly interacting theories, TC and QCD, are interconnected by corrections due to ETC and other interactions. These SDE are displayed in Fig. 1. These diagrams appear naturally when QCD and TC are embedded into a larger gauge group, like, for instance, the \(SU(5)_S\) Farhi–Susskind model [49] which plays the role of the ETC group. These gap equations may also contain electroweak corrections and, as we are not specifying a model, other possible interactions, which may contribute to the last diagram on the right-hand side of Fig. 1.

In the work of Ref. [40] the SDE equations were solved numerically and we just commented, without presenting the details of the calculation, that the effect of the radiative corrections in the coupled equations change the (UV) boundary conditions of the TC gap equation. As we comment in the introductory section, the purpose of this work is to show in detail how the coupled system (TC and QCD) have their boundary conditions changed by the ETC radiative corrections in such a way that the self-energies ultraviolet behavior turn out to be of the form that we may call extreme walking or irregular one. With this purpose in this section we show that the set of coupled equations obtained in Ref. [40], Eqs. (4) and (5), assuming the approximation shown in Eq. (6), lead to a set of coupled differential equations, and, independently of the numerical solution obtained in [40] , in the present work we show, considering the analytical solution of this coupled system, that the dynamic effect of including the QCD degrees of freedom lead to a change in the boundary conditions of the TC gap equation, in the same way that TC changes the boundary conditions of the ordinary fermions gap equations generating their current masses.

The diagrams denoted by \(a_i\) and \(b_i\) with \(i=1\) in Fig. 1 are respectively the known SDE for techniquarks and quarks. These equations become coupled through the ETC interactions as indicated by the diagrams \(a_2\) and \(b_2\). We shall not discuss the effect of diagrams \(a_3\) and \(b_3\), which were briefly discussed in Ref. [40]. The TC SDE (diagram \(a_1\)), whose self-energy, coupling constant and respective Casimir operator will be indicated by the index (1), receives a correction (diagram \(a_2\)) due to the quarks self-energy indicated by the index (2) with charge \(C_E\alpha _E\) and gauge boson mass \(M_E\) related to the ETC group, leading to the following equation [40]

$$\begin{aligned} \varSigma _1(p)= & {} \frac{3C_1\alpha _1}{2\pi ^2}\int dk^2 dA \frac{k^2\varSigma _1(k^2)}{(p-k)^2[k^2+\varSigma ^2_1(k^2)]} \nonumber \\&+\frac{3C_E\alpha _E}{2\pi ^2}\int dk^2 dA \frac{k^2\varSigma _{2}(k^2)}{k^2+\varSigma ^2_{2}(k^2)}\frac{1}{(p-k)^2 + M^2_E},\nonumber \\ \end{aligned}$$
(4)

whereas for the quarks self-energy we have a similar equation just changing the index \(1 \leftrightarrow 2\)

$$\begin{aligned} \varSigma _2(p)= & {} \frac{3C_2\alpha _2}{2\pi ^2}\int dk^2 dA \frac{k^2\varSigma _2(k^2)}{(p-k)^2[k^2+\varSigma ^2_2(k^2)]}\nonumber \\&+\frac{3C_E\alpha _E}{2\pi ^2} \int dk^2 dA \frac{k^2\varSigma _1(k^2)}{[(p-k)^2+M_E^2]\cdot [k^2+\varSigma ^2_1 (k^2)]},\nonumber \\ \end{aligned}$$
(5)

where \(dA=d\theta \sin ^2{\theta }\).

We can easily identify the second term in right-hand side of Eq. (5) as the usual quark mass obtained through TC interaction. With the appropriate QCD values for \(C_2 \alpha _2\) and ETC values for \(C_E \alpha _E\) and \(M_E\) we obtain a solution that is the sum of the dynamical quark mass with its effective “bare mass”. Also Eq. (4) provides the dynamical techniquark mass with a very tiny mass generated by the QCD correction.

The above equations were solved numerically in Ref. [40]. Here they will be transformed into a coupled system of differential equations, therefore we will need to make a few simplifications and the first one is to perform the angular integration using the angle approximation [50], transforming the following terms as

$$\begin{aligned} \frac{1}{(p - k)^2 + M^2} = \frac{\pi }{2}\left\{ \frac{\theta (p - k)}{p^2 + M^2} + \frac{\theta (k - p)}{k^2 + M^2}\right\} , \end{aligned}$$
(6)

where in the sequence we may take \(M = M_E\) or \(M = 0 \).

Note that the approximations that we perform are reasonable. Even the fact that we do not consider more sophisticated vertices is justifiable because the extra contributions to the SDE are essentially perturbative contributions.

Continuing with the notation \((1\equiv TC)\) and \( (2\equiv QCD) \) we obtain the following form for the system of coupled integral equations

$$\begin{aligned}&f_1(x)= \sigma _1(x)I^a_1(x) {+} \theta _1I^b_1(x) {+} \zeta _{12}(x)I^a_2(x) {+} \eta _{12}I^b_{E2}(x) \nonumber \\&f_2(x)= \sigma _2(x)I^a_2(x) {+} \theta _2I^b_2(x) {+} \zeta _{21}(x)I^a_1(x) {+} \eta _{21}I^b_{E1}(x).\nonumber \\ \end{aligned}$$
(7)

To arrive at the last expression we introduced the following set of new variables and auxiliary functions

$$\begin{aligned}&p^2 = M^2_ix,\,\,\, \varSigma _i(p^2) = M_i f_i(x),\,\,\, \omega _{i} =\frac{m^2_i}{M^2_i}\nonumber \\&k^2 = M^2_iy,\,\,\,\varSigma _i(k^2) = M_i f_i(y),\,\,\, \beta _{i} =\frac{M^2}{M^2_i}\nonumber \\&\sigma _i(x) = \frac{\theta _i}{x + \omega _i},\,\,\,\theta _i =\frac{3C_i\alpha _i}{4\pi },\,\,\,\theta _E =\frac{3C_E\alpha _E}{4\pi } \nonumber \\&I^a_i(x) = \int ^{x}_{0}dy\frac{yf_i(y)}{y+f^2_i(y)},\,\,\,g_i(x) = \frac{xf_i(x)}{x+f^2_i(x)} \nonumber \\&I^b_i(x) = \int ^{\frac{\varLambda ^2}{M^2_i}}_{x} dy\frac{yf_i(y)}{y+f^2_ i(y)}\frac{1}{y +\omega _i} \nonumber \\&I^b_{Ei}(x) = \int ^{\frac{\varLambda ^2}{M^2_i}}_{x} dy\frac{yf_i(y)}{y+f^2_ i(y)}\frac{1}{y +\beta _i} \nonumber \\&\zeta _{ij}(x) = \frac{\theta _E}{x+\beta _i}\left( \frac{M_j}{M_i}\right) ^3,\,\,\,\eta _{ij} = \theta _E\left( \frac{M_j}{M_i}\right) . \end{aligned}$$
(8)

In the above expressions \(M=M_{E}\), \(i,j=1(2)\) denote the contributions of TC(QCD) to the coupled gap equation. Note that \(M_1 = \mu _{{}_{1}}\), and \(M_2 = \mu _{{}_{2}}\), where \(\mu _i\) correspond respectively to the dynamical TC and QCD fermionic mass scales, \(m_i\) represents technigluons(or gluons) dynamical mass scale [51,52,53,54], which were not considered in Ref. [40].

In order to transform the coupled system of integral equations described by Eq. (7) into a system of coupled differential equations for \(f_i(x)\) we also introduce new functions \(\delta _1(x)\) and \(\delta _2(x)\) , where

$$\begin{aligned} \delta _1(x)= & {} \frac{\zeta '_{12}(x) \left( f'_2(x) + \frac{\eta _{21}g_1(x)}{x+\beta _1} - \zeta _{21}(x)g_1(x)\right) }{\zeta '_{12}(x)\zeta '_{21}(x) - \sigma '_2(x)\sigma '_1(x)} \nonumber \\&- \frac{\sigma '_2(x)\left( f'_1(x) + \frac{\eta _{12}g_2(x)}{x+\beta _2} - \zeta _{12}(x)g_2(x)\right) }{\zeta '_{12}(x)\zeta '_{21}(x) - \sigma '_2(x)\sigma '_1(x)} \end{aligned}$$
(9)
$$\begin{aligned} \delta _2(x)= & {} \frac{ \zeta '_{21}(x) \left( f'_1(x) + \frac{\eta _{12}g_2(x)}{x+\beta _2} - \zeta _{12}(x)g_2(x)\right) }{\zeta '_{12}(x)\zeta '_{21}(x) - \sigma '_2(x)\sigma '_1(x)} \nonumber \\&-\frac{\sigma '_1(x)\left( f'_2(x) + \frac{\eta _{21}g_1(x)}{x+\beta _1} - \zeta _{21}(x)g_1(x)\right) }{\zeta '_{12}(x)\zeta '_{21}(x) - \sigma '_2(x)\sigma '_1(x)}, \end{aligned}$$
(10)

in such a way that now we can write

$$\begin{aligned} f''_1(x)+ & {} \frac{\eta _{12}g'_2(x)}{x +\beta _2} + \frac{\zeta _{12}(x)g_2(x)}{x+\beta _1} = \frac{\eta _{12}g_2(x)}{(x+\beta _2)^2} \nonumber \\&+ \,\zeta _{12}(x)g'_2(x) + \sigma ''_1(x)\delta _1(x) + \sigma '_1(x)\delta '_1(x) \nonumber \\&+ \frac{{}^{}}{{}^{}}\zeta ''_{12}(x)\delta _2(x) + \zeta '_{12}(x)\delta '_2(x) \end{aligned}$$
(11)
$$\begin{aligned} f''_2(x)+ & {} \frac{\eta _{21}g'_1(x)}{x +\beta _1} + \frac{\zeta _{21}(x)g_1(x)}{x+\beta _2} = \frac{\eta _{21}g_1(x)}{(x+\beta _1)^2} \nonumber \\&+ \, \zeta _{21}(x)g'_1(x) + \sigma ''_2(x)\delta _2(x) + \sigma '_2(x)\delta '_2(x) \nonumber \\&+ \frac{{}^{}}{{}^{}}\zeta ''_{21}(x)\delta _1(x) + \zeta '_{21}(x)\delta '_1(x). \end{aligned}$$
(12)

It is an exercise the verification that Eqs. (11) and (12) can be solved by a linear combination of two solutions. One that is called regular, where the self-energies behave at large momenta as 1 / x, and another one, called irregular, where the self-energies decrease as \([\ln x ]^{-\epsilon }\), where \(\epsilon \) is a function of the quantities b and c. Only when the boundary conditions are applied to these equations the actual self-energy ultraviolet behavior is selected. This is the central point of the work of Ref. [40] and the one that we present here: The ETC radiative corrections cause the selection of the irregular solution and not the one behaving as 1 / x!

How the ETC corrections will change the SDE boundary conditions and the solution behavior will be shown in the next section. However, in a very naive approximation for Eq. (5) we can show in the sequence that quark masses vary logarithmically with the ETC mass scale (i.e. \(M_E\)), which is a consequence of a TC self-energy with a logarithmic ultraviolet (UV) behavior [40]. As can be seen from Eq. (5) the full quark mass (\(m_q\)) is a sum of the dynamical mass generated within QCD, with the one generated through TC mediated by the ETC interaction. Using Eq. (6) and approximating \(m_q\) by \(\varSigma _2(0)\) we can simplify Eq. (5) and obtain

$$\begin{aligned} m_q\approx & {} \varSigma _2 (0) \approx \frac{3C_2\alpha _2}{4\pi }\int _{0}^\varLambda dk^2\frac{\varSigma _2(k)}{k^2 +\varSigma ^2_2(k)} \nonumber \\&+\frac{3C_E\alpha _E}{4\pi }\int _{0}^\varLambda dk^2\frac{\varSigma _1(k)}{k^2+\varSigma ^2_1(k)}\frac{1}{k^2 + M^2_E} \nonumber \\&+\frac{3C_2\alpha _2}{4\pi }\frac{1}{M^2_E}\int _{0}^\varLambda dk^2\frac{\varSigma _2(k)}{k^2 +\varSigma ^2_2(k)} \nonumber \\&+\frac{3C_E\alpha _E}{4\pi }\frac{1}{2M^2_E}\int _{0}^\varLambda dk^2\frac{\varSigma _1(k)}{k^2+\varSigma ^2_1(k)} \end{aligned}$$
(13)

This is an oversimplified equation compared to Eq. (5) and gives \(m_q\) as a function of \(M_E\). We can now input the solutions of Eqs. (11) and (12) into Eq. (13) and solve it up to the convergence. The convergence is obtained only with the solution that has a logarithmic UV behavior.

Even within the simplified approach shown above it is possible to compare the calculation of Eq. (13) with the full numerical result obtained in Ref. [40]. Therefore, assuming \(\varLambda = 500\)  TeV, \(M_1 = \mu _{1}= 1\) TeV, \(M_2 =\mu _{2} = 0.3\) GeV, \(C_1 \alpha _1=6\) and \(C_2 \alpha _2=1.16\) values such that isolated techniquark and quark masses were equal respectively to \(\mu _1\) and \(\mu _2\) as in Ref. [40], and \(C_E \alpha _E = 0.032\), we plot \(m_q\) as a function of \(M_E\) in Fig. 2.

Fig. 2
figure 2

Behavior of \(m_q\) as a function of \(M_E\) obtained from Eq. (13) using the solutions of Eqs. (12) and (11) (red curve ()). The blue curve () corresponds to the result obtained in [40]. The dot-dash lines represents the Fit(1) (blue dot-dash line) and Fit(2) (red dot-dash line) , the parameters are described in the text

Full size image

The blue curve () corresponds to the result obtained in [40], while the red curve () is the numerical one obtained with Eqs. (11)–(13). The dot-dash lines represent the fit

$$\begin{aligned} m_q^{fit} \propto a_1 [ln(M^2_E/M^2_{2})]^{-a_2}, \end{aligned}$$
(14)

where for the Fit(1) (blue dot-dash) we obtain , \(a_1= 203.92\)GeV and \(a_2= 2.53\) with \(R^2=0.99\) and for Fit(2) (red dot-dash) , \(a_1= 1620\) GeV and \(a_2=3.6\) with \(R^2=0.93\). The behavior exhibited by the curves in Red depicted in Fig. 2 are very similar to the one obtained in the Ref. [40]. The small discrepancy between these different results can be credited to the angle approximation and the simple approximation made here to calculate \(m_q\).

In ETC models, as the one-family Farhi–Susskind model [49], a consequence of the breaking of an approximate \(SU(8)_L \times SU(8)_R\) chiral symmetry, is the appearance in the spectrum of a wide variety of pseudo-Goldstone bosons. Therefore, we may wonder what happens with pseudo-Goldstone bosons in the scenario we are proposing here. The diagram \((a_1)\) of Fig. 1 will generate a dynamical TC mass at a TeV scale. Assuming that technifermions have an electroweak or other similar charge, the diagrams \((a_2)\) and \((a_3)\) of Fig. 1 will generate effective “bare” masses \(m_T\) of order of GeV, definitively raising the pseudo-Goldstone boson masses (\(m_\varPi \)), what may be concluded using simply the Gell–Mann–Oakes–Renner relation, \(m_\varPi ^2 \approx m_T {\left\langle { {\bar{\psi }}_T}\psi _T\right\rangle }/2F_{\varPi }^2\), where \(F_\varPi \) is the technipion decay constant, leading to \(m_\varPi \approx O(100) GeV\). Moreover, the main point in this work and in the one of Ref. [40] is to stress the logarithmic behavior of the TC and QCD self-energies. Since the radiative corrections due to electroweak (or other) interactions to the pseudo-Goldstone boson masses involve the coupling of the pseudo-Goldstone bosons to the the technifermions (i.e. the technipion vertex) and this vertex is proportional to the self-energy, which does not decrease anymore as \(1/p^2\), therefore the corrections to the pseudo-Goldstone masses are larger. In Ref. [40] these corrections were estimated to be \(m_\varPi \propto g_A^2(\mu ^2_{TC}/F_\varPi ^2)M_A^2\), where \(g_A\) is the coupling constant of the radiative correction induced by the electroweak (or other) boson A with mass \(M_A\). Although the calculation is model dependent the resulting mass values may evade the existent experimental limits.

3 UV boundary conditions induced by ETC radiative corrections

In order to determine the boundary conditions of our SDE coupled system we can differentiate Eq. (7) obtaining

$$\begin{aligned}&f'_1(x) = \sigma '_1(x)I^a_1(x) + \zeta '_{12}(x)I^a_2(x) \nonumber \\&f'_2(x) = \sigma '_2(x)I^a_2(x) + \zeta '_{21}(x)I^a_1(x), \end{aligned}$$
(15)

from these expressions and reconsidering Eq. (7) in the asymptotic UV limit, such that \((\frac{\varLambda ^2}{M^2_i} = \frac{M^2_E}{M^2_i}>> 1)\) we end up the following set of coupled equations

$$\begin{aligned}&f_1(x) + xf'_1(x) = \zeta _{12}(x)I^a_2(x)\nonumber \\&f_2(x) + xf'_2(x) = \zeta _{21}(x)I^a_1(x) \end{aligned}$$
(16)

which correspond to the UV boundary conditions that should be satisfied by Eqs. (11) and (12). Reconsidering the definitions of variables and auxiliary functions described in Eq. (8) the above expressions above lead to

$$\begin{aligned}&\left[ \varSigma _1(p^2) + p^2\varSigma '_1(p^2)\right] _{p^2\rightarrow \infty } = m_2 ,\nonumber \\&\left[ \varSigma _2(p^2) + p^2\varSigma '_2(p^2)\right] _{p^2\rightarrow \infty } = m_1 , \end{aligned}$$
(17)

where

$$\begin{aligned} m_{1(2)}=\frac{3C_E\alpha _E}{4\pi }\int dk^2\frac{k^2\varSigma _{1(2)}(k^2)}{k^2+\varSigma ^2_{1(2)}(k^2)}\frac{1}{k^2 + M^2_E} . \end{aligned}$$
(18)

It is easy to recognize that Eq. (17) when \(\alpha _E =0\), i.e. when the equations are decoupled, we have

$$\begin{aligned}&\left[ \varSigma _1(p^2) + p^2\varSigma '_1(p^2)\right] _{p^2\rightarrow \infty } = 0,\nonumber \\&\left[ \varSigma _2(p^2) + p^2\varSigma '_2(p^2)\right] _{p^2\rightarrow \infty } = 0 , \end{aligned}$$
(19)

and it has long been known that the asymptotic behavior of \(\varSigma _1(p^2)\) (or \(\varSigma _2(p^2)\)) is described by [14]

$$\begin{aligned} \varSigma _{1(2)}(p^2 \rightarrow \infty )\propto \frac{\mu ^3_{1(2)}}{p^2} \end{aligned}$$
(20)

which lead to quark masses \(m_q\approx \varSigma _2 (0)\) of order

$$\begin{aligned} m_q \approx C_E\alpha _E\frac{M^3_1}{M_E^2}, \end{aligned}$$
(21)

which is at the origin of all known problems of TC models [9].

When we turn on the ETC interaction, i.e. \(\alpha _E \ne 0\), the Eq. (17) differ only by their infrared (IR) boundary conditions, which are usually set as \(\varSigma _1 (0)=M_1\) and \(\varSigma _2 (0)=M_2\). If, apart only from different numerical scales, we set \(\varSigma _1 (0)=\varSigma _2 (0)\equiv M \) Eq. (17) will give

$$\begin{aligned}&\left[ \varSigma _1(p^2) + p^2\varSigma '_1(p^2)\right] _{p^2\rightarrow \infty } = M(p^2\rightarrow \infty ) , \nonumber \\&\left[ \varSigma _2(p^2) + p^2\varSigma '_2(p^2)\right] _{p^2\rightarrow \infty } = M(p^2\rightarrow \infty ) , \end{aligned}$$
(22)

where \( M(p^2\rightarrow \infty ) \propto M[\ln p^2/M^2 ]^{-\epsilon }\) and there is no doubt that \(\varSigma _1(p^2)\) and \(\varSigma _2(p^2)\) have exactly the same IR and UV behavior, and when \(M_1\ne M_2\) they just differ numerically in the IR but have the same functional expression. This is a confirmation of the statement in Ref. [40] that in the scenario proposed there the TC and QCD self-energies have exactly the same UV asymptotic behavior.

If we do not assume the same IR conditions for both self-energies we can again verify that \(\varSigma _1(p^2)\) and \(\varSigma _2(p^2)\) have formally the same UV behavior. Initially we can observe that in the deep Euclidean region we have

$$\begin{aligned} f_i (x \rightarrow \infty ) \approx \frac{\theta _i}{x} \delta _i (x), \end{aligned}$$
(23)

but in the same limit and after some algebra we can see that \(\delta _1 (x)\) and \(\delta _2 (x)\) have also the same expression apart from a constant, therefore

$$\begin{aligned} \left. f_1 (x)\right| _{x\rightarrow \infty } \propto \left. f_2 (x)\right| _{x\rightarrow \infty }, \end{aligned}$$
(24)

indicating that both self-energies decrease equally in the UV region.

The main difference in the UV boundary conditions in the decoupled and coupled SDE, assuming that \(\varSigma _1 (p^2)\) and \(\varSigma _2 (p^2)\) have the same formal expression and both can be substituted by an expression \(\varSigma (p^2)\), is an effective mass term

$$\begin{aligned} m=\frac{3C_E\alpha _E}{4\pi }\int dk^2\frac{k^2\varSigma (k^2)}{k^2+\varSigma ^2 (k^2)}\frac{1}{k^2 + M^2_E} , \end{aligned}$$
(25)

and this term is going to act like a “bare” mass, whose effect is to generate a logarithmically decreasing self-energy for quarks and techniquarks. The fact that the self-energies are logarithmically decreasing with momenta and technifermions also acquire a small mass, can also explain how the pseudo Nambu–Goldstone mesons obtain a large mass and may evade constraints from LHC data (see Ref. [40]). The hard self-energies may also be responsible for the decrease of the scalar composite mass [42, 43].

4 Conclusions

In the Ref. [40] we have given evidences that radiative corrections to TC(QCD) change the UV technifermion(quark) self-energy behavior. This happens when TC and QCD are embedded into an unified theory as in the Farhi–Susskind model (or an ETC model). In this work we verify that in these cases the radiative corrections that couple the different strongly interacting Dyson equations induce new boundary conditions for the gap equations and change the UV behavior compared to the isolated equations.

We transformed the coupled TC and QCD coupled equations into a pair of differential equations. These two equations may have as a solution a linear combination of the known regular and irregular self-energies. When these solutions are applied to a quite simplified mass equation (Eq. (13)), derived from the original gap equation, we verified that quark masses vary logarithmically with the ETC scale, what is a consequence of a TC self-energy that also decreases logarithmically with the momentum. This is a simple confirmation of the more complete numerical calculation of Ref. [40]. The simple quark mass (Eq. (13)) acts as a constraint for the differential equations solution, appearing as an effective mass boundary condition.

In Sect. 3 we discussed how the ETC interaction induce a change into the boundary conditions, and this change is equivalent to the addition of an effective bare mass to the gap equation, which leads naturally to a self-energy logarithmically decreasing with the momentum. Moreover, as stated in Ref. [40], we also discussed that both self-energies have the same formal expression and, along with the discussion of that same reference, may lead to a new way to build TC models.