A new decay mode of higher charmonium

Abstract

We calculate the $\Lambda _c{\bar{\Lambda }}_c$ partial decay width of the excited vector charmonium states around 4.6 GeV with the quark pair creation model. We find that the partial decay width of the $\Lambda _c{\bar{\Lambda }}_c$ mode can reach up to several MeV for $\psi (4S,~5S,~6S)$. In contrast, the partial $\Lambda _c{\bar{\Lambda }}_c$ decay width of the states $\psi (3D,~4D,~5D)$ is less than one MeV. If the enhancement Y(4630) reported by the Belle Collaboration in $\Lambda _c{\bar{\Lambda }}_c$ invariant-mass distribution is the same structure as Y(4660), the Y(4660) resonance is most likely to be a S-wave charmonium state.

1 Introduction

Since the Belle Collaboration reported the first member of the family of the charmonium-like states, X(3872), in 2003 [1], a series of charmonium-like states [2], called collectively XYZ states, have been observed by several major experimental collaborations such as Babar, BESIII, LHCb, CLEO-c and so on. To date, dozens of charmonium-like states [2] have been discovered. The charmonium systems may provide unique clues to the nonperturbative behavior of QCD in the low energy regime and have attracted a great deal of attention from the hadron physics community; see Ref. [3] for a review and references.

The Y(4660) resonance, as the most massive state among the charmonium-like states at present, was first reported by the Belle Collaboration [4] in the process $e^+e^-\rightarrow \gamma _{\text {ISR}}\pi ^+\pi ^-\psi (2S)$ associated with the Y(4360) resonance in 2007. Its mass and width were determined to be $M=(4664\pm 16)$ MeV and $\Gamma =(48\pm 18)$ MeV, respectively. Later, this state was confirmed by BaBar Collaboration [5] in the $\pi ^+\pi ^-\psi (2S)$ invariant-mass distribution with new data on the $e^+e^-\rightarrow \gamma _{\text {ISR}}\pi ^+\pi ^-\psi (2S)$ progress with the mass $M=(4669\pm 24)$ MeV and width $\Gamma =(104\pm 58)$ MeV. Since the Y(4660) resonance was produced from the $e^+e^-$ annihilation, the quantum number is $J^{PC}=1^{--}$. Besides, the Belle Collaboration reported an enhancement, Y(4630), in the cross section of the $e^+e^-\rightarrow \Lambda ^+_c\Lambda ^-_c$ in 2008 [6], whose mass and width are consistent within the errors with those of Y(4660). Hence, these two states may be the same structure although they were observed in different processes [7,8,9].

Table 1 The possible assignments of the Y(4660) with the predicted masses (MeV) from various models

Over the past decade, the properties of the charmonium-like state Y(4660) were extensively explored with various theoretical methods. In the framework of the screened potential model by Li and Chao [10], Y(4660) was a good candidate of the $\psi (6S)$ state. However, Ding et al. [11] interpreted Y(4660) as the $\psi (5S)$ state in the flux tube model, which is consistent with the prediction in Refs. [12, 13]. Besides the interpretation of the conventional charmonium states, Y(4660) was also interpreted as a tetraquark state [14,15,16,17,18,19,20,21,22,23], $f_0(980)\psi '$ bound state [24,25,26,27], baryonium [8, 28] and hadro-charmonium state [29] and so on. In addition, van Beveren et al. [30] argued that Y(4660) should not be associated with a resonance pole of the $c\bar{c}$ propagator by analyzing the published Babar data for the reaction $e^+e^-\rightarrow D^*{\bar{D}}^*$  [31]. For the properties of Y(4630), there are many theoretical interpretations as well [32,33,34,35,36,37,38].

According to the mass and spin-parity, the possible assignments of Y(4660) as a charmonium state are $\psi (4S)$, $\psi (5S)$, $\psi (6S)$, $\psi (3D)$, $\psi (4D)$, or $\psi (5D)$, which have been listed in Table 1. In the framework of the quark pair creation model (QPC model), we calculate the decay width of the $\Lambda _c{\bar{\Lambda }}_c$ mode for those vector charmonium states and obtain that (1) if the Y(4660) is a S-wave charmonium state, the partial decay width of the $\Lambda _c{\bar{\Lambda }}_c$ mode can reach several MeV. However, if the Y(4660) is a D-wave charmonium state, the partial decay width of the $\Lambda _c{\bar{\Lambda }}_c$ mode should be less than one MeV. (2) If the enhancement Y(4630) reported by Belle Collaboration in $\Lambda _c{\bar{\Lambda }}_c$ invariant-mass distribution is the same structure as Y(4660), the Y(4660) resonance is most likely to be a S-wave charmonium state.

This paper is organized as follows. In Sect. 2 we give a brief introduction of the QPC model. Then, we present our numerical results and discussions in Sect. 3 and summarize our results in Sect. 4.

2 An introduction of the $^3P_0$ model

The QPC model is known as $^3P_0$ model, which was first proposed by Micu [39], Carlitz and Kislinger [40], and further developed by the Orsay group [41,42,43,44]. This model is widely used to study the OZI-allowed strong decays of hadrons. In the model, a quark pair $q\bar{q}$ is created from the vacuum and then regroups with the quarks within the initial hadron to produce two outgoing hadrons. In particular, the interaction Hamiltonian for one quark pair creation was assumed as [45,46,47]

$$\begin{aligned} H_{q\bar{q}}=\gamma \sum _f2m_f\int d^3x\bar{\psi }_f\psi _f, \end{aligned}$$

(1)

where $m_f$ is the constituent quark mass of flavor f, $\psi _f$ denotes a Dirac quark field, and $\gamma$ is a dimensionless parameter describing the $q\bar{q}$ pair-production strength, which is usually fixed by fitting to the well measured decay widths.

Fig. 1

The charmonium system decays into a $\Lambda _c{\bar{\Lambda }}_c$ pair

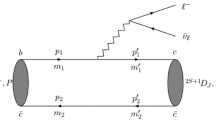
In this work, we extend the $^3P_0$ model to study the charmonium system decaying into a $\Lambda _c{\bar{\Lambda }}_c$ pair. For this type of reaction, it is necessary to create two light quark pairs, which is shown in Fig. 1. In the framework of the $^3P_0$ model, the helicity amplitude $M^{M_{J_A}M_{J_B}M_{J_B}}$ for the process of $Y(4660)(A)\rightarrow \Lambda _c(B)+{\bar{\Lambda }}_c(C)$ reads

$$\begin{aligned}&\delta ^3(\mathbf {p}_A-\mathbf {p}_B-\mathbf {p}_C)M^{M_{J_A}M_{J_B}M_{J_B}}\nonumber \\&\quad =\frac{\sum _k\langle BC|H_{q\bar{q}}|k\rangle \langle k|H_{q\bar{q}}|A\rangle }{E_k-E_A}. \end{aligned}$$

(2)

Here, $\mathbf {p}_A(\mathbf {p}_B/\mathbf {p}_C)$ represents the momentum of the hadron A(B / C). $E_k$ and $E_A$ stand for the energy of the intermediate state k and initial state A, respectively. To simplify the calculations, we take $E_k-E_A$ as a constant, namely $E_k-E_A\equiv 2m_{q}$. This approximation is reasonable because the intermediate state just have two more created quarks compared to the initial state at the quark level. On the other hand, the allowed intermediate states with the spin parity $J^{PC}=1^{--}$ are $D{\bar{D}}_1$, $D^*{\bar{D}}_1$, $D^*{\bar{D}}_0$, $D^*{\bar{D}}_2$, $J/\Psi f_0(500)/f_0(600)$, $h_c(1P)\eta$, $h_c(1P)\pi$, $\chi _{c0}(1P)\omega (782)$ and $\chi _{c2}(1P)\omega (782)$ and tetraquark states [14] and so on. Their masses are about $\sim 4.0$ GeV. Thus, we use $E_k-E_A\sim 0.6$ GeV $\sim 2m_q$. Under the above approximation, we can rewrite the Eq. (2) as

$$\begin{aligned} \delta ^3(\mathbf {p}_A-\mathbf {p}_B-\mathbf {p}_C)M^{M_{J_A}M_{J_B}M_{J_B}}=\frac{\langle BC|H_{q\bar{q}}H_{q\bar{q}}|A\rangle }{2m_{q}}, \end{aligned}$$

(3)

where $m_{q}$ is the mass of the created quark pair.

In the nonrelativistic limit, the transition operator for the two quark pairs creation under the $^3P_0$ model is given by

$$\begin{aligned} T= & {} \frac{9\gamma ^2}{4m_{\mu }} \sum _{m,m'}\langle 1m;1-m|00\rangle \langle 1m';1-m'|00\rangle \nonumber \\&\times \int d^3\mathbf {p}_3d^3\mathbf {p}_4d^3\mathbf {p}_5d^3\mathbf {p}_6\delta ^3(\mathbf {p}_3 +\mathbf {p}_4)\delta ^3(\mathbf {p}_5+\mathbf {p}_6)\nonumber \\&\times \varphi ^{34}_0\omega ^{34}_0\chi ^{34}_{1,-m} \mathcal {Y}_1^m\left( \frac{\mathbf {p}_3-\mathbf {p}_4}{2}\right) a^{\dagger }_{3i} b^{\dagger }_{4j}\nonumber \\&\times \varphi ^{56}_0\omega ^{56}_0\chi ^{56}_{1,-m'} \mathcal {Y}_1^{m'}\left( \frac{\mathbf {p}_5-\mathbf {p}_6}{2}\right) a^{\dagger }_{5i} b^{\dagger }_{6j}, \end{aligned}$$

(4)

where $\mathbf {p}_i$ ($i=3$, 4, 5, 6) corresponds to the three-vector momentum of the ith quark within the two created quark pairs. $\varphi _0=(u\bar{u}+d\bar{d}+s\bar{s})/\sqrt{3}$ and $\omega _0=\delta _{ij}$ correspond to the flavor function and color singlet, respectively. The solid harmonic polynomial $\mathcal {Y}_1^{m(m')}(\mathbf {p})\equiv |\mathbf {p}|Y^{m(m')}_1(\theta _p,\phi _p)$ stand for the P-wave quark pairs, and $\chi _{1,-m(m')}$ are the spin triplet states for the created quark pairs. $a^{\dagger }_{i}b^{\dagger }_{j}$ is the creation operator denoting the quark pairs creation in the vacuum.

Adopting the definition of the mock state [54], the meson (A) and baryon (B) states are defined as, respectively,

$$\begin{aligned}&|A(N_A~^{2S_A+1}L_A{J_AM_{J_A}})(\mathbf {p}_A)\rangle =\sqrt{2E_A}\varphi ^{12}_A\omega ^{12}_A\nonumber \\&\quad \times \sum _{M_{L_A},M_{S_A}}\langle L_AM_{L_A};S_AM_{S_A}|J_AM_{J_A}\rangle \nonumber \\&\quad \times \int d^3\mathbf {p}_1d^3\mathbf {p}_2\delta ^3(\mathbf {p}_1+\mathbf {p}_2-\mathbf {p}_A)\nonumber \\&\quad \times \Psi _{N_AL_AM_{L_A}(\mathbf {p}_1,\mathbf {p}_2)}\chi ^{12}_{S_AM_{S_A}}|q_1 (\mathbf {p}_1)q_2(\mathbf {p}_2)\rangle , \end{aligned}$$

(5)

$$\begin{aligned}&|B(N_B~^{2S_B+1}L_B{J_BM_{J_B}})(\mathbf {p}_B)\rangle =\sqrt{2E_B}\varphi ^{135}_B\omega ^{135}_B\nonumber \\&\quad \times \sum _{M_{L_B},M_{S_B}}\langle L_BM_{L_B};S_BM_{S_B}|J_BM_{J_B}\rangle \nonumber \\&\quad \times \int d^3\mathbf {p}_1d^3\mathbf {p}_3d^3\mathbf {p}_5\delta ^3(\mathbf {p}_1 +\mathbf {p}_3+\mathbf {p}_5-\mathbf {p}_B)\nonumber \\&\quad \times \Psi _{N_BL_BM_{L_B}(\mathbf {p}_1,\mathbf {p}_3,\mathbf {p}_5)} \chi ^{135}_{S_BM_{S_B}} |q_1(\mathbf {p}_1)q_3(\mathbf {p}_3)q_5(\mathbf {p}_5)\rangle . \end{aligned}$$

(6)

The $\mathbf {p}_i~(i=1,2,3,5)$ denotes the momentum of quarks in hadrons A and B. Since the $^3P_0$ model obtains a reasonable description of the decay properties of many mesons with the simple harmonic oscillator (SHO) wave functions, which are a de facto standard for many nonrelativistic quark model calculations [45, 46, 55,56,57], we adopt the SHO wave functions to describe the space-wave functions of the baryons in this work. Meanwhile, with the simple SHO wave functions the decay amplitudes can be calculated analytically, which are helpful to understand the general decay behavior. The SHO wave function of a meson without radial excitations reads

$$\begin{aligned} \psi ^0_{lm}(\mathbf {p})= & {} (-i)^l\Bigg [\frac{2^{l+2}}{\sqrt{\pi }(2l+1)!!} \Bigg ]^{\frac{1}{2}}\Bigg (\frac{1}{\beta }\Bigg )^{l+\frac{3}{2}}\nonumber \\&\times \text {exp}\Bigg (-\frac{\mathbf {p}_R^2}{2\beta ^2}\Bigg )\mathcal {Y}_l^m(\mathbf {p}), \end{aligned}$$

(7)

and the ground state space-wave function of a baryon reads

$$\begin{aligned} \psi _{0,0}=3^{\frac{3}{4}}\Bigg (\frac{1}{\pi \alpha _{\rho }^2}\Bigg )^{\frac{3}{4}} \Bigg (\frac{1}{\pi \alpha _{\lambda }^2}\Bigg )^{\frac{3}{4}} \text {exp}\Bigg (-\frac{\mathbf {p}_{\rho }^2}{2\alpha _{\rho }^2} -\frac{\mathbf {p}_{\lambda }^2}{2\alpha _{\lambda }^2}\Bigg ). \end{aligned}$$

(8)

Fig. 2

The $\rho$- and $\lambda$-mode excitations of the cqq system where $\rho$ and $\lambda$ are the jacobi coordinates defined as $\rho =\frac{\mathbf {r}_1-\mathbf {r}_2}{\sqrt{2}}$ and $\lambda =\frac{\mathbf {r}_1+\mathbf {r}_2-2\mathbf {r}_3}{\sqrt{6}}$, respectively. $q_1$ and $q_2$ represent the light (u, d) quark, and $Q_3$ represents the charm quark

Here the $\mathbf {p}_R$ stands for the relative momentum between the quark and antiquark within the meson. $\mathbf {p}_{\rho }$ and $\mathbf {p}_{\lambda }$ stand for the momentum corresponding to $\rho$ and $\lambda$ jacobi coordinates (see Fig. 2), respectively. Thus, we can obtain the helicity amplitude in the center of mass frame,

$$\begin{aligned}&{\mathcal {M}}^{M_{J_A}M_{J_B}M_{J_C}}(A\rightarrow B+C) =\frac{9\gamma ^2}{4m_{\mu }}\sqrt{8E_AE_BE_C}\nonumber \\&\quad \times \prod _{A,B,C}\langle \chi ^{135}_{S_BM_{S_B}} \chi ^{246}_{S_CM_{S_C}}|\chi ^{12}_{S_AM_{S_A}}\chi ^{34}_{1-m}\chi ^{56}_{1-m'}\rangle \nonumber \\&\quad \times \langle \omega ^{135}_B\omega ^{246}_C|\omega ^{12}_A\omega ^{34}_0\omega ^{56}_0\rangle \langle \varphi ^{135}_B\varphi ^{246}_C|\varphi ^{12}_A\varphi ^{34}_0\varphi ^{56}_0\rangle I^{M_{L_A},m,m'}_{M_{L_B},M_{L_C}}(\mathbf {p}).\nonumber \\ \end{aligned}$$

(9)

Here, $I^{M_{L_A},m,m'}_{M_{L_B},M_{L_C}}(\mathbf {p})$ stands the spatial integral and more detailed calculations are shown in the Appendix. The $\prod _{A,B,C}$ corresponds to the Clebsch–Gorden coefficients for the two created quark pairs, initial and final hadrons, which come from the couplings among the spin, orbital, and total angular momentum. Its specific expression is

$$\begin{aligned}&\sum \langle L_AM_{L_A};S_AM_{S_A}|J_AM_{J_A}\rangle \langle 1m;1-m|00\rangle \langle 1m'; 1-m'|00\rangle \nonumber \\&\quad \times \langle L_BM_{L_B};S_BM_{S_B}|J_BM_{J_B}\rangle \langle L_CM_{L_C};S_CM_{S_C}|J_CM_{J_C}\rangle . \end{aligned}$$

(10)

Finally, with the relativistic phase space, the hadronic decay width $\Gamma [A\rightarrow BC]$ reads

$$\begin{aligned} \Gamma [A\rightarrow BC]= & {} \pi ^2\frac{|\mathbf {p}|}{M_A^2}\frac{1}{2J_A+1}\nonumber \\&\times \sum _{M_{J_A},M_{J_B},M_{J_C}}| {\mathcal {M}}^{M_{J_A}M_{J_B}M_{J_C}}|^2. \end{aligned}$$

(11)

In the equation, the momentum $\mathbf {p}$ of the daughter baryon in the center of mass frame of the parent baryon A is

$$\begin{aligned} |\mathbf {p}|=\frac{\sqrt{\left[ M_A^2-(M_B-M_C)^2\right] \left[ M_A^2-(M_B+M_C)^2\right] }}{2M_A}. \end{aligned}$$

(12)

In the present calculation, we adopt $m_u$ = $m_d$ = 330 MeV and $m_c=1628$ MeV for the constituent quark masses. The masses of the baryons $\Lambda _c$ and ${\bar{\Lambda }}_c$ are taken as $m_{\Lambda _c}$ = $m_{\overline{\Lambda }_c}$ = 2286.46 MeV, which are from the Particle Data Group [2]. The harmonic oscillator strength $\beta$ for the excitation between the two charm quarks in initial charmonium system (see Fig. 2) is adopted as 500 MeV  [52]. The parameter $\alpha _{\rho }$ of the $\rho$-mode excitation between the two light quarks in final single-heavy baryons is taken the average value as $\alpha _{\rho }=400$ MeV, and the other harmonic oscillator parameter $\alpha _{\lambda }$ is obtained with the following relation [58,59,60]:

$$\begin{aligned} \alpha _{\lambda }=\Bigg (\frac{3m_Q}{2m_q+m_Q}\Bigg )^{1/4}\alpha _{\rho }. \end{aligned}$$

(13)

In this equation, $m_Q$ stands for the constituent quark mass of charmed quark, and $m_q$ responds the constituent quark mass of light quark ($q=u,~d$).

For the strength of the quark pair creation from the vacuum, we adopt the definition from Ref. [61], where $\gamma$ is a scale-dependent form,

$$\begin{aligned} \gamma (\mu )=\frac{\gamma _0}{\text {log}(\frac{\mu }{\mu _0})}. \end{aligned}$$

(14)

Here, $\mu$ is the reduced mass of the quark-antiquark in the decaying meson, and $\gamma _0=0.81\pm 0.02$ and $\mu _0=(49.84\pm 2.58)$ MeV. According to Eq. (14), we get $\gamma (\mu )=0.29$ with the mass of $m_c=1628$ MeV. So, the strength of the quark pair creation employed in this work is $\gamma =5.04$ which is $\sqrt{96\pi }$ times of that in Ref. [61] due to a different definition [46, 52, 62]. The uncertainty of the strength $\gamma$ is around $30\%$ [47, 62,63,64] and the partial decay width is proportional to $\gamma ^4$, so the uncertainty of our theoretical results may be quite large.

3 Calculations and results

The quantum number of the Y(4660) resonance is determined to be $J^P=1^{--}$ from the $e^+e^-$ annihilation. The average values of mass and width listed in PDG [2] are $M=(4643\pm 9)$ MeV and $\Gamma _{\text {total}}=72\pm 11$ MeV, respectively. Around 4660 MeV, there are six vector charmonium states, which are $\psi (4S)$, $\psi (5S)$, $\psi (6S)$, $\psi (3D)$, $\psi (4D)$, and $\psi (5D)$. In the following, we will discuss the decay properties of these states.

3.1 S wave

The theoretical mass of $\psi (5^3S_1)$ is about 4.64 GeV (see Table 1), which is in good agreement with the mass of Y(4660) in PDG [2]. In addition, via evaluating the open flavor strong decays, some people interpreted Y(4660) as a $\psi (5S)$ state in the flux tube model [11] and QPC model [12], respectively. As the possibel assignment of Y(4660), it is crucial to study the decay properties of the $\psi (5^3S_1)$.

Table 2 The $\Lambda _c{\bar{\Lambda }}_c$ partial decay widths (MeV) of the vector charmonium with a mass of $M=4643$ MeV

Fig. 3

The variation of the $\Lambda _c\overline{\Lambda }_c$ decay width with the mass of the S-wave vector charmonium. The blue, black, and red lines correspond to the predictions with different values of the harmonic oscillator strength $\beta =450$, 500, and 550 MeV, respectively

Fig. 4

The variation of the $\Lambda _c\overline{\Lambda }_c$ decay width with the mass of the D-wave vector charmonium. The blue, black, and red lines correspond to the predictions with different values of the harmonic oscillator strength $\beta =450$, 500, and 550 MeV, respectively

According to our calculations, we get

$$\begin{aligned} \Gamma [\psi (5^3S_1)\rightarrow \Lambda _c{\bar{\Lambda }}_c]\sim 2.44~\text {MeV} \end{aligned}$$

(15)

with a mass of $M=4643$ MeV (see Table 2). Combing the measured width of Y(4660), we further predict the branching ratio

$$\begin{aligned} {\mathcal {B}}[\psi (5^3S_1)\rightarrow \Lambda _c{\bar{\Lambda }}_c]\sim 3\%. \end{aligned}$$

(16)

The sizeable branching ratio indicates that this state has a good potential to be observed in the $\Lambda _c{\bar{\Lambda }}_c$ decay channel.

Meanwhile, considering the uncertainties of the predicted mass, we plot the variation of the partial decay width of the $\Lambda _c{\bar{\Lambda }}_c$ mode as a function of the mass of the state $\psi (5^3S_1)$ in Fig. 3. The decay width of the $\Lambda _c{\bar{\Lambda }}_c$ mode increases with the mass increasing in the range of (4580–4602) MeV, and the width can reach up to $\Gamma \sim 3.4$ MeV. However, when the mass increases in the range of (4603–4800) MeV, the partial decay width decreases.

Besides $\psi (5^3S_1)$, we also investigate the decay properties of the states $\psi (4^3S_1)$ and $\psi (6^3S_1)$. The predicted masses of these two states are listed in Table 1. From the Table 1 it is seen that the possibility of Y(4660) taken as the state $\psi (4^3S_1)$ or $\psi (6^3S_1)$ can’t be excluded completely. Fixing the masses at $M=4643$ MeV, we obtain

$$\begin{aligned} \Gamma [\psi (4^3S_1)\rightarrow \Lambda _c{\bar{\Lambda }}_c]\sim 6.57~\text {MeV}, \end{aligned}$$

(17)

and

$$\begin{aligned} \Gamma [\psi (6^3S_1)\rightarrow \Lambda _c{\bar{\Lambda }}_c]\sim 0.84~\text {MeV}. \end{aligned}$$

(18)

The predicted decay widths are large enough to be observed in experiments. Moreover,

$$\begin{aligned} \frac{\Gamma [\psi (4^3S_1)\rightarrow \Lambda _c{\bar{\Lambda }}_c]}{\Gamma [\psi (5^3S_1)\rightarrow \Lambda _c{\bar{\Lambda }}_c]}\sim 2.7. \end{aligned}$$

(19)

The branching ratio of $\psi (4^3S_1)$ decaying into $\Lambda _c{\bar{\Lambda }}_c$ pair is larger than that of $\psi (5^3S_1)$.

Meanwhile, if the Y(4660) resonance corresponds to $\psi (6^3S_1)$, the branching ratio is predicted to be

$$\begin{aligned} {\mathcal {B}}[\psi (6^3S_1)\rightarrow \Lambda _c{\bar{\Lambda }}_c]\sim 1\%. \end{aligned}$$

(20)

This branching ratio is the smallest, while it is quite large compared to the ratio (${\mathcal {O}}(10^{-3})\sim {\mathcal {O}}(10^{-5})$) of other charmonium states decaying into the baryon-antibaryon pair [2].

In addition, we also plot the decay width of the $\psi (4^3S_1)$ and $\psi (6^3S_1)$ as a function of the mass in the range of $M=(4580{-}4800)$ MeV in Fig. 3. The variation curves between the partial decay width and the mass for these two states are similar to that for $\psi (5^3S_1)$.

In brief, we have calculated the $\Lambda _c{\bar{\Lambda }}_c$ partial decay widths of the three S-wave states $\psi (4^3S_1)$, $\psi (5^3S_1)$, and $\psi (6^3S_1)$ with the QPC model. According to our predictions, the $\Lambda _c{\bar{\Lambda }}_c$ decay width can reach up to a few MeV. If Y(4660) is a vector charmonium, it is very likely to be found in the $\Lambda _c{\bar{\Lambda }}_c$ channel.

3.2 D wave

The predicted mass of the state $\psi (4^3D_1)$ is listed in Table 1. This state is a good candidate of the Y(4660) resonance. So it is necessary to investigate the decay properties of $\psi (4^3D_1)$.

In the same way, we fix the mass of $\psi (4^3D_1)$ at $M=4643$ MeV firstly. Then, we obtain the partial decay width

$$\begin{aligned} \Gamma [\psi (4^3D_1)\rightarrow \Lambda _c{\bar{\Lambda }}_c]\sim 0.19~\text {MeV}. \end{aligned}$$

(21)

This width seems not large, but it is enough to be observed in this decay channel in experiments. Moreover, the branching ratio is predicted to be

$$\begin{aligned} {\mathcal {B}}[\psi (4^3D_1)\rightarrow \Lambda _c{\bar{\Lambda }}_c]\sim 0.3\%. \end{aligned}$$

(22)

We also plot the variation of the $\Lambda _c{\bar{\Lambda }}_c$ decay width as a function of the mass in Fig. 4. From the Fig. 4, the partial decay width for $\psi (4^3D_1)$ decaying into the $\Lambda _c{\bar{\Lambda }}_c$ pair is less than $\sim 1.3$ MeV in the range of $(4580-4800)$ MeV.

Furthermore, we analyze the decay properties of the states $\psi (3^3D_1)$ and $\psi (5^3D_1)$, and collect their predicted masses in Table 1. From the Table 1, the theoretical masses are either about ($100\sim 200$) MeV lighter or heavier than the mass of Y(4660) in PDG [2]. We also study the decay properties of the two states in this work.

Taking the masses of the $\psi (3^3D_1)$ and $\psi (5^3D_1)$ as $M=4643$ MeV, we get that the partial decay widths are

$$\begin{aligned} \Gamma [\psi (3^3D_1)\rightarrow \Lambda _c{\bar{\Lambda }}_c]\sim 0.33~\text {MeV} \end{aligned}$$

(23)

and

$$\begin{aligned} \Gamma [\psi (5^3D_1)\rightarrow \Lambda _c{\bar{\Lambda }}_c]\sim 0.09~\text {MeV}. \end{aligned}$$

(24)

If the Y(4660) were the state $\psi (5^3D_1)$, one would be very hard to observe Y(4660) in the $\Lambda _c{\bar{\Lambda }}_c$ channel.

The predicted masses of the states $\psi (3^3D_1)$ and $\psi (5^3D_1)$ certainly have a large uncertainty, which may bring uncertainties to our theoretical results. To investigate this effect, we plot the partial decay widths of these two states as functions of the masses in Fig. 4 as well.

The $\Lambda _c{\bar{\Lambda }}_c$ decay widths of the D-wave states are less than one MeV. The $\Lambda _c{\bar{\Lambda }}_c$ decay width ratio between the S-wave states and D-wave states is ${\mathcal {O}}(10)$. If Y(4660) turns out to be a S-wave state, it has a good potential to be observed in the $\Lambda _c{\bar{\Lambda }}_c$ channel.

3.3 The effect of $\beta$

We have considered six excited vector charmonium states around 4.6 Gev and investigated their $\Lambda _c{\bar{\Lambda }}_c$ partial decay width. In the present work, all of the theoretical predictions are obtained with the parameter $\beta =500$ MeV. However, the harmonic oscillator parameter $\beta$ for the excitation between the charm quarks in initial charmonium system is not determined precisely, which bares a large uncertainty. To investigate the uncertainties of the parameter $\beta$, we further consider the decay properties as a function of the mass with two different $\beta$ values: $\beta =450$, 550 MeV. The numerical results are shown in Figs. 3 and 4. One notes that the bigger $\beta$ value leads to a larger decay width. Our main predictions hold in a reasonable range of the parameter $\beta$.

4 Summary

In the present work, we calculate the $\Lambda _c{\bar{\Lambda }}_c$ partial decay width of the excited vector charmonium around 4.6 GeV, including $\psi (4S,~5S,~6S)$ and $\psi (3D,~4D,~5D)$. The $\Lambda _c{\bar{\Lambda }}_c$ mode is not kinematically allowed for the charmonium states below 4.6 GeV. This OZI allowed mode provides a new tool to explore the higher charmonium, which will be produced abundantly at Belle-II. We extend the original $^3P_0$ model and consider the creation of two light $q\bar{q}$ pairs from the vacuum, which is the first attempt along this direction in literatures up to our knowledge.

Based on our calculations, the decay widths of the S-wave states decaying into the $\Lambda _c{\bar{\Lambda }}_c$ pair are about a few MeV, while the $\Lambda _c{\bar{\Lambda }}_c$ decay widths of the D-wave states are less than one MeV. The $\Lambda _c{\bar{\Lambda }}_c$ decay width ratio between the S-wave states and the D-wave states is ${\mathcal {O}}(10)$. If the Y(4660) is one of the S-wave states considered in this work, it may be observed in the $\Lambda _c{\bar{\Lambda }}_c$ channel. Moreover, if the enhancement Y(4630) reported by Belle collaboration in $\Lambda _c{\bar{\Lambda }}_c$ invariant-mass distribution is the same structure as the Y(4660), the Y(4660) is very likely to be a S-wave charmonium state. On the other hand, it will be very difficult to observe the excited D-wave vector charmonium in the $\Lambda _c{\bar{\Lambda }}_c$ channel. In other words, the $\Lambda _c{\bar{\Lambda }}_c$ mode can be used to pin down the internal structure of the vector charmonium.

Appendix A: The amplitude calculations

The harmonic oscillator wave functions for the ground charmed baryons B(C) in our calculation are

$$\begin{aligned} \psi ^{B(C)}(0,~0,~0,~0)= & {} 3^{\frac{3}{4}}\Bigg (\frac{1}{\pi \alpha _{\rho }^2}\Bigg )^{\frac{3}{4}}\Bigg (\frac{1}{\pi \alpha _{\lambda }^2}\Bigg )^{\frac{3}{4}} \nonumber \\&\times \exp \Bigg [-\frac{P_{\rho }^2}{2\alpha _{\rho }^2}-\frac{P_{\lambda }^2}{2\alpha _{\lambda }^2}\Bigg ], \end{aligned}$$

(A1)

where $\mathbf {p}^{B(C)}_{\rho }=\frac{1}{\sqrt{2}}(\mathbf {p}_{3(2)}-\mathbf {p}_{5(4)})$ and $\mathbf {p}^{B(C)}_{\lambda }=\frac{1}{\sqrt{6}}(\mathbf {p}_{3(2)} +\mathbf {p}_{5(4)}-2\mathbf {p}_{1(2)})$.

The ground state wave function of the meson is

$$\begin{aligned} \Psi (0,~0)=\Bigg (\frac{1}{\pi \beta ^2}\Bigg )^{\frac{3}{4}} \exp \Bigg [-\frac{(\mathbf {p}_1-\mathbf {p}_2)^2}{8\beta ^2}\Bigg ] \end{aligned}$$

(A2)

Since all the final states are in the S-wave states in this calculations, the momentum space integration $I^{M_{L_A},m,m'}_{M_{L_B}M_{L_C}}(\mathbf {p})$ can be further expressed as $\prod (M_{L_A},m,m')$.

For the 1S charmonium state decay:

$$\begin{aligned} \Pi (0,~0,~0)= & {} \Bigg (\frac{1}{\pi \alpha _{\rho }^2}\Bigg )^{\frac{3}{2}}\Bigg (\frac{1}{\pi \alpha _{\lambda }^2}\Bigg )^{\frac{3}{2}}\Bigg (\frac{1}{\pi \beta ^2}\Bigg )^{\frac{3}{4}}\nonumber \\&\times \exp \Bigg [-\Bigg (\lambda _4-\frac{\lambda ^2_3}{4\lambda _2}\Bigg )P^2_B\Bigg ] \nonumber \\&\times \frac{\pi ^2}{16}\left( \frac{1}{\lambda _1\lambda _2}\right) ^{\frac{3}{2}} \left( 12\varpi ^2P_B^2-\frac{3}{\lambda _1}+\frac{1}{\lambda _2}\right) , \nonumber \\ \end{aligned}$$

(A3)

$$\begin{aligned} \Pi (0,1,-1)= & {} \Bigg (\frac{1}{\pi \alpha _{\rho }^2}\Bigg )^{\frac{3}{2}}\Bigg (\frac{1}{\pi \alpha _{\lambda }^2}\Bigg )^{\frac{3}{2}}\Bigg (\frac{1}{\pi \beta ^2}\Bigg )^{\frac{3}{4}}\nonumber \\&\times \exp \Bigg [-\Bigg (\lambda _4 -\frac{\lambda ^2_3}{4\lambda _2}\Bigg )P^2_B\Bigg ] \nonumber \\&\times \frac{\pi ^2}{16}\Bigg (\frac{1}{\lambda _1\lambda _2} \Bigg )^{\frac{3}{2}}\Bigg (\frac{3}{\lambda _1}-\frac{1}{\lambda _2}\Bigg )\nonumber \\= & {} \Pi (0,-1,1). \end{aligned}$$

(A4)

For the 1D charmonium state decay:

$$\begin{aligned} \Pi (0,~0,~0)= & {} \Bigg (\frac{1}{\pi \alpha _{\rho }^2}\Bigg )^{\frac{3}{2}}\Bigg (\frac{1}{\pi \alpha _{\lambda }^2}\Bigg )^{\frac{3}{2}}\Bigg (\frac{1}{\beta ^2}\Bigg )^{\frac{7}{4}}\nonumber \\&\times \exp \Bigg [-\Bigg (\lambda _4 -\frac{\lambda ^2_3}{4\lambda _2}\Bigg )P^2_B\Bigg ] \nonumber \\&\times \pi ^{\frac{5}{4}}\Bigg (\frac{1}{\lambda _1\lambda _2}\Bigg )^{\frac{3}{2}} \Bigg (\frac{\sqrt{3}}{2}\zeta ^2\varpi ^2P^4_B +\frac{\zeta ^2P^2_B}{8\sqrt{3}\lambda _2}\nonumber \\&-\frac{\sqrt{3}\zeta ^2P^2_B}{8\lambda _1}-\frac{\zeta \varpi P^2_B}{\sqrt{3} \lambda _2}+\frac{\sqrt{3}}{36\lambda ^2_2}\Bigg ), \end{aligned}$$

(A5)

$$\begin{aligned} \Pi (0,~1,-1)= & {} \Bigg (\frac{1}{\pi \alpha _{\rho }^2}\Bigg )^{\frac{3}{2}}\Bigg (\frac{1}{\pi \alpha _{\lambda }^2}\Bigg )^{\frac{3}{2}}\Bigg (\frac{1}{\beta ^2}\Bigg )^{\frac{7}{4}}\nonumber \\&\quad \times \exp \Bigg [-\Bigg (\lambda _4-\frac{\lambda ^2_3}{4\lambda _2}\Bigg )P^2_B\Bigg ] \nonumber \\&\quad \times \pi ^{\frac{5}{4}}\Bigg (\frac{1}{\lambda _1\lambda _2}\Bigg )^{\frac{3}{2}} \Bigg ( \frac{\sqrt{3}\zeta ^2P^2_B}{8\lambda _1}-\frac{\zeta ^2P^2_B}{8\sqrt{3}\lambda _2} +\frac{\sqrt{3}}{72\lambda ^2_2}\Bigg )\nonumber \\= & {} \Pi (0,-1,1), \end{aligned}$$

(A6)

$$\begin{aligned} \Pi (1,-1,0)= & {} \Bigg (\frac{1}{\pi \alpha _{\rho }^2}\Bigg )^{\frac{3}{2}}\Bigg (\frac{1}{\pi \alpha _{\lambda }^2}\Bigg )^{\frac{3}{2}}\Bigg (\frac{1}{\beta ^2}\Bigg )^{\frac{7}{4}}\nonumber \\&\quad \times \exp \Bigg [-\Bigg (\lambda _4-\frac{\lambda ^2_3}{4\lambda _2}\Bigg )P^2_B\Bigg ] \nonumber \\&\quad \times \pi ^{\frac{5}{4}}\Bigg (\frac{1}{\lambda _1\lambda _2}\Bigg )^{\frac{3}{2}} \Bigg ( \frac{\zeta \varpi P^2_B}{4\lambda _2}-\frac{1}{24\lambda ^2_2}\Bigg )\nonumber \\= & {} \Pi (1,0,-1), \end{aligned}$$

(A7)

$$\begin{aligned} \Pi (2,-1,-1)= & {} \Bigg (\frac{1}{\pi \alpha _{\rho }^2}\Bigg )^{\frac{3}{2}}\Bigg (\frac{1}{\pi \alpha _{\lambda }^2}\Bigg )^{\frac{3}{2}}\Bigg (\frac{1}{\beta ^2}\Bigg )^{\frac{7}{4}}\nonumber \\&\quad \times \exp \Bigg [-\Bigg (\lambda _4-\frac{\lambda ^2_3}{4\lambda _2}\Bigg )P^2_B\Bigg ] \end{aligned}$$

(A8)

$$\begin{aligned}&\quad \times \pi ^{\frac{5}{4}}\Bigg (\frac{1}{\lambda _1\lambda _2}\Bigg )^{\frac{3}{2}} \frac{\sqrt{2}}{24\lambda ^2_2}. \end{aligned}$$

(A9)

Here,

$$\begin{aligned} \lambda _1= & {} \frac{1}{\alpha ^2_{\rho }}, \end{aligned}$$

(A10)

$$\begin{aligned} \lambda _2= & {} \frac{1}{\alpha ^2_{\lambda }}+\frac{1}{3\beta ^2}, \end{aligned}$$

(A11)

$$\begin{aligned} \lambda _3= & {} -\frac{\sqrt{6}}{9\beta ^2}, \end{aligned}$$

(A12)

$$\begin{aligned} \lambda _4= & {} \frac{1}{18\beta ^2}, \end{aligned}$$

(A13)

$$\begin{aligned} \varpi= & {} \frac{1}{3}-\frac{\lambda _3}{2\sqrt{6}\lambda _2}, \end{aligned}$$

(A14)

$$\begin{aligned} \zeta= & {} \frac{1}{3}+\frac{\lambda _3}{\sqrt{6}\lambda _2}, \end{aligned}$$

(A15)

for the above expressions. $|P_B|$ reads as

$$\begin{aligned} |P_B|=\frac{\sqrt{\big [m^2_A-(m_B+m_C)^2\big ]\big [m^2_A-(m_B-m_C)^2\big ]}}{2m_A}.\nonumber \\ \end{aligned}$$

(A16)

With the amplitudes for the 1S states decaying into two S-wave final states, we can obtain the radially and orbitally excited states’ amplitudes which are related to the lowest radial or orbital states by differentiation [65],

$$\begin{aligned} {\mathcal {M}}_{4S}= & {} \frac{1}{3\sqrt{35}}\Bigg (15\beta \frac{\partial }{\partial \beta }+6\beta ^2\frac{\partial ^2}{\partial \beta ^2} +2\beta ^3\frac{\partial ^3}{\partial \beta ^3}\Bigg ){\mathcal {M}}_{1S}, \end{aligned}$$

(A17)

$$\begin{aligned} {\mathcal {M}}_{5S}= & {} \frac{1}{18\sqrt{70}}\Bigg (63+72\beta \frac{\partial }{\partial \beta }+96\beta ^2\frac{\partial ^2}{\partial \beta ^2} +24\beta ^3\frac{\partial ^3}{\partial \beta ^3}\nonumber \\&+4\beta ^4\frac{\partial ^4}{\partial \beta ^4}\Bigg ){\mathcal {M}}_{1S}, \end{aligned}$$

(A18)

$$\begin{aligned} {\mathcal {M}}_{6S}= & {} \frac{1}{45\sqrt{77}}\Bigg (\frac{675}{2}\beta \frac{\partial }{\partial \beta }+240\beta ^2\frac{\partial ^2}{\partial \beta ^2} +120\beta ^3\frac{\partial ^3}{\partial \beta ^3}\nonumber \\&+20\beta ^4\frac{\partial ^4}{\partial \beta ^4}+2\beta ^5\frac{\partial ^5}{\partial \beta ^5}\Bigg ){\mathcal {M}}_{1S}, \end{aligned}$$

(A19)

$$\begin{aligned} {\mathcal {M}}_{3D}= & {} \frac{1}{3\sqrt{14}}\Bigg (7+2\beta \frac{\partial }{\partial \beta }+2\beta ^2\frac{\partial ^2}{\partial \beta ^2} \Bigg ){\mathcal {M}}_{1D}, \end{aligned}$$

(A20)

$$\begin{aligned} {\mathcal {M}}_{4D}= & {} \frac{1}{3\sqrt{231}}\Bigg (27\beta \frac{\partial }{\partial \beta }+6\beta ^2\frac{\partial ^2}{\partial \beta ^2} +2\beta ^3\frac{\partial ^3}{\partial \beta ^3}\Bigg ){\mathcal {M}}_{1D}, \end{aligned}$$

(A21)

$$\begin{aligned} {\mathcal {M}}_{5D}= & {} \frac{1}{6\sqrt{6006}}\Bigg (231+120\beta \frac{\partial }{\partial \beta }+144\beta ^2\frac{\partial ^2}{\partial \beta ^2} +24\beta ^3\frac{\partial ^3}{\partial \beta ^3}\nonumber \\&+4\beta ^4\frac{\partial ^4}{\partial \beta ^4}\Bigg ){\mathcal {M}}_{1D}. \end{aligned}$$

(A22)