Inclusive study of bottomonium production in association with an $\eta$ meson in $e^+e^-$ annihilations near $\varUpsilon (5S)$

Abstract

We study bottomonium production in association with an $\eta$ meson in $e^+e^-$ annihilations near the $\varUpsilon (5S)$, at a centre-of-mass energy of $\sqrt{s}=10.866$ GeV. The results are based on the 121.4 fb$^{-1}$ data sample collected by the Belle experiment at the asymmetric-energy KEKB collider. Only the $\eta$ meson is reconstructed and the missing-mass spectrum of $\eta$ candidates is investigated. We observe the $e^+e^-\rightarrow \eta \varUpsilon _J(1D)$ process and find evidence for the $e^+e^-\rightarrow \eta \varUpsilon (2S)$ process, while no significant signals of $\varUpsilon (1S)$, $h_b(1P)$, nor $h_b(2P)$ are found. Cross sections for the studied processes are reported.

The treatment of the non-perturbative regime of Quantum Chromodynamics represents one of the major open problems in particle physics [1]. Quarkonia – bound states of either b and $\bar{b}$ or c and $\bar{c}$ quarks – are regarded as one of the most fertile environments in which new theoretical approaches to this quandary can be tested [2], thanks to the intrinsic multiscale nature of their dynamics, which are characterized by the coexistence of hard and soft processes [3]. The richness of this sector has been shown by the wave of new discoveries from the BaBar, Belle and CLEO experiments, and then BESIII and LHCb, that challenged the prevailing theoretical models for quarkonium spectra and transitions. Unexpected neutral and charged states have been observed in both charmonium and bottomonium, together with striking violations of the Okubo–Zweig–Iizuka (OZI) rule [4,5,6] and Heavy Quark Spin Symmetry (HQSS). These have demonstrated that the light-quark degrees of freedom play a crucial role in the description of spectral properties [7] and transitions [8]. For a recent review of the theoretical models of quarkonia, see Refs. [9, 10].

The study of transitions that violate HQSS, like those on which this work is focused, is therefore part of a broader topic of studying exotic quarkonium-like states. HQSS and the models based on it, like the QCD Multipole Expansion  [11,12,13,14,15,16], have been long considered reliable for describing hadronic transitions in bottomonium. In this approach, the transitions can be classified into favoured non-spin flipping, like $\varUpsilon (nS) \rightarrow \pi \pi \varUpsilon (mS)$, and disfavoured spin-flipping, like $\varUpsilon (nS) \rightarrow \eta \, \varUpsilon (mS)$, which are suppressed by a factor of $(\varLambda _{\mathrm {QCD}}/m_b)^2$. As a result of this suppression, the small ratio of branching fractions

$$\begin{aligned} \mathcal {R}^{\eta S}_{\pi \pi S}(n,m)= \frac{\mathcal {B}[\varUpsilon (nS)\rightarrow \eta \varUpsilon (mS)]}{\mathcal {B}[\varUpsilon (nS)\rightarrow \pi ^+\pi ^-\varUpsilon (mS)]} \approx 10^{-3} \end{aligned}$$

is predicted [17, 18], providing a simple, sensitive and experimentally accessible test of HQSS. HQSS has been verified at $\varUpsilon (2S)$ and $\varUpsilon (3S)$, with $\mathcal {R}^{\eta S}_{\pi \pi S}(2,1)= (1.64\pm 0.23)\times 10^{-3}$ [19,20,21] and $\mathcal {R}^{\eta S}_{\pi \pi S}(3,1)<2.3\times 10^{-3}$ [20] but not at $\varUpsilon (4S)$: BaBar unexpectedly observed the HQSS-violating transition $\varUpsilon (4S)\rightarrow \eta \varUpsilon (1S)$ with a branching fraction of $(1.96\pm 0.28)\times 10^{-4}$, $2.41\pm 0.42$ larger than the one for the favoured transition $\varUpsilon (4S)\rightarrow \pi \pi \varUpsilon (1S)$ [22]. A recent Belle measurement [23] then confirmed this result. This strong disagreement with the HQSS prediction was explained by the contribution of B meson loops or, equivalently, by the presence of a four-quark $B\bar{B}$ component within the $\varUpsilon (4S)$ wave function [24, 25]. In the case of transitions to spin-singlet states, there is still no evidence of $\varUpsilon (4S) \rightarrow \pi \pi h_b(1P)$, while the $\varUpsilon (4S) \rightarrow \eta h_b(1P)$ has been observed recently by Belle to be the largest hadronic transition from the $\varUpsilon (4S)$ [26], with a branching fraction in agreement with theoretical arguments [27, 28] based on various treatments of the light-quark contributions. At the $\varUpsilon (5S)$ energy [29, 30], the $\varUpsilon (5S) \rightarrow \pi \pi h_b(mP)$ transitions, which were expected to be suppressed by the HQSS violation, have been observed by Belle to be enhanced by the presence of intermediate exotic, four-quark states [31, 32]. Finally, the $\varUpsilon (5S) \rightarrow \omega \chi _{b1}(1P)$ transition has been observed by Belle to be enhanced with respect to the $\varUpsilon (5S) \rightarrow \omega \chi _{b2}(1P)$ [33], contrary to the HQSS expectation if the $\varUpsilon (5S)$ were a pure $b\bar{b}$ state [34].

Fig. 1

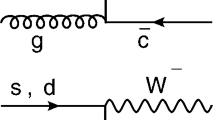
Example of triangular B meson loops diagram expected to contribute to the $\varUpsilon (5S) \rightarrow \eta \varUpsilon _J(1D)$ transition, from [37]

This paper is devoted to the study of one of the missing experimental pieces in the puzzle of the hadronic transitions in bottomonium: the single-$\eta$ emission from the $\varUpsilon (5S)$ region to $\varUpsilon (1S)$, $\varUpsilon (2S)$, $\varUpsilon _J(1D)$, $h_b(1P)$ and $h_b(2P)$. The final states with $\varUpsilon (1S)$ and $\varUpsilon (2S)$ have been studied by theorists using rescattering models [24] or by considering intermediate hybrids [35]. The predictions are affected by large uncertainties but agree within one order of magnitude with a preliminary result reported by Belle [36] that was obtained via the exclusive reconstruction of the $\varUpsilon (1S, 2S)$ decay into muons. In a recent work [37], the case of $\varUpsilon (5S) \rightarrow \eta \varUpsilon _J(1D)$ is analyzed in the context of a rescattering model where the $\varUpsilon (5S)$ decays via triangular $B^{(\star )}$ meson loops, as shown in Fig. 1. The branching fractions are calculated to be of the order of $10^{-3}$, and precise predictions for the contributions due to the three components of the 1D triplet are given:

$$\begin{aligned} f_1 = \frac{\mathcal{B}[\varUpsilon (5S) \rightarrow \eta \varUpsilon _1(1D)]}{\mathcal{B}[\varUpsilon (5S) \rightarrow \eta \varUpsilon (1D_2)]} = 0.68 \end{aligned}$$

and

$$\begin{aligned} f_3 = \frac{\mathcal{B}[\varUpsilon (5S) \rightarrow \eta \varUpsilon _3(1D)]}{\mathcal{B}[\varUpsilon (5S) \rightarrow \eta \varUpsilon (1D_2)]} = 0.13. \end{aligned}$$

Our analysis is performed using the 121.4 fb$^{-1}$ sample of $e^+e^-$ collisions collected by the Belle experiment nearby the $\varUpsilon (5S)$ energy. Following the approach used for the study of $h_b(nP)$ production in $e^+e^-$ collisions at the $\varUpsilon (5S)$ [29] and $\varUpsilon (4S)$ [26] energies, we investigate the missing-mass spectrum of $\eta$ mesons in hadronic events. The missing mass is defined as the Lorentz-invariant quantity $M_\mathrm{miss}(\eta ) c=\sqrt{(P_{e^+e^-}-P_{\eta })^2}$, where $P_{e^+e^-}$ and $P_{\eta }$ are, respectively, the four-momenta of the colliding $e^+e^-$ pair and the reconstructed $\eta$ meson.

The Belle experiment [38] at the KEKB asymmetric $e^+e^-$ collider [39,40,41] is a $4\pi$ spectrometer optimized for the study of $CP-$violation effects in B meson decays. We highlight here the main characteristics of the apparatus, which is described in detail elsewhere [42]. The tracking of charged particles is provided by four layers of double-sided silicon strip detectors (SVD) and a 50-layer drift chamber (CDC). The energy of photons and electrons is measured by an electromagnetic calorimeter (ECL), while particle identification is obtained by combining the specific ionization measured in the CDC, the time of flight measured by a double layer of plastic scintillators (TOF) and the yield of Cherenkov radiation detected by the Aerogel Cherenkov Counter (ACC). These devices are embedded in a 1.5T axial magnetic field provided by a cylindrical superconducting solenoid. The iron return yoke of the magnet is instrumented with resistive plate chambers to track and identify muons and $K_L$ mesons. The ECL, which is pivotal for the present measurement, is constructed of CsI(Tl) crystals arranged in a nearly projective geometry to maximize the hermeticity. The central cylindrical barrel covers the polar angle range of $32.2^{\circ }< \theta < 128.7^{\circ }$ while the forward and backward endcap extend the coverage to $\theta = 12^{\circ }$ and $\theta = 158^{\circ }$, respectively. The z axis is opposite to the positron beam.

Studies of the background, optimization of the selection criteria, and estimation of the efficiency are performed using Monte Carlo (MC) samples of the signal processes (signal MC), and of the $e^+e^- \rightarrow B^{(*)}\bar{B^{(*)}}(\pi )$, $e^+e^- \rightarrow B^{(*)}_s\bar{B}^{(*)}_s$ and $e^+e^- \rightarrow q \bar{q}$ ($q= u,d,s,c$) reactions (generic MC). The samples are generated using EvtGen [43], while the detector response is simulated with GEANT3 [44]. The annihilation of bottomonium into light hadrons, as well as the hadronization of the quarks produced in continuum processes, is simulated by Pythia6  [45]. The angular distributions of the signal processes are generated assuming the lower angular momentum amplitudes to be dominant. Separate MC samples are generated for each run period to account for evolution in the detector performance and accelerator conditions. Each selection criterion is optimized separately, maximizing the figure of merit $F = N_{S}/\sqrt{N_B}$, where $N_{S(B)}$ is the number of signal (background) events passing the selection. To ensure that the selection is independent of the $\eta$ meson momentum, most of the optimization is performed using as signal all the $\eta$ mesons present in the generic MC samples. The signal MC is used only to optimize the suppression of $e^+e^- \rightarrow q \bar{q}$ events and to estimate the reconstruction efficiency.

The analysis procedure is similar to the one described in Ref. [26], where the process $\varUpsilon (4S) \rightarrow \eta \, b\bar{b}$ is considered. An $\eta$ candidate is reconstructed in the $\gamma \gamma$ channel only; the 3$\pi$ modes, both charged and neutral, are not considered due to the low reconstruction efficiency and larger combinatorial background. The $\gamma$ candidates are selected from energy deposits in the ECL not associated with charged tracks. ECL clusters induced by neutral hadrons are suppressed by requiring the shower’s transverse-profile radius to be less than 5.1 cm and the ratio of the energy deposits in a 3 $\times$ 3 and 5 $\times$ 5 crystal matrix around the cluster center to be greater than 0.9. Since the beam-induced background produces low-energy clusters mostly in the endcap regions, we apply a minimum photon energy threshold that varies as a function of the cluster polar angle: $E_{\gamma } > 75$ MeV in the backward ECL endcap, $E_{\gamma } > 50$ MeV in the backward half of the barrel, $E_{\gamma } > 60$ MeV in the forward barrel, and $E_{\gamma } > 95$ MeV in the forward endcap. The absolute photon energy and the ECL resolution are calibrated by comparing, respectively, the peak position and the widths of three calibration signals, $\pi ^0 \rightarrow \gamma \gamma$, $\eta \rightarrow \gamma \gamma$, and $D^{*0} \rightarrow D^{0}\gamma$, in the MC sample and the data [30]. Averaging the results from the different samples, we obtain an energy-scale correction $\mathcal{F}_{en}(E) = (0.67 \pm 0.25)\%$ at $E_{\gamma } = 0.1$ GeV, that first decreases to $(0.05 \pm 0.23)\%$ at $E_{\gamma } = 0.7$ GeV, and then increases again up to $(0.30 \pm 0.20)\%$ at $E_{\gamma } = 1.4$ GeV. The resolution correction factor decreases smoothly with the photon energy $E_{\gamma }$, from $\mathcal{F}_{res}(E) = (25 \pm 10)\%$ at $E_{\gamma } = 0.1$ GeV to $(1 \pm 3)\%$ at $E_{\gamma } = 1.4$ GeV. These are used to calibrate the simulated events. An iterative $\pi ^0$-veto procedure removes from the $\eta$-candidate daughter list the photons that are associated with a $\pi ^0 \rightarrow \gamma \gamma$ decay. Such photons are selected from pairs with an invariant mass $M(\gamma \gamma )$ within 17 MeV/$c^2$ of the nominal $\pi ^0$ mass $m_{\pi ^0}$ [46]. At each iteration, we remove from the $\eta$ daughter list the photon pair with mass closest to $m_{\pi ^0}$, and we update the $\pi ^0$ list so that the excluded photons are not used to construct further $\pi ^0$ candidates. Finally, we exploit the scalar nature of the $\eta$ to further suppress the combinatorial background, by requiring the photon helicity angle (i.e., the angle $\theta$ between the photon direction and that of the $\varUpsilon (5S)$ in the $\eta$ rest frame) to satisfy $\cos \theta < 0.94$. The distribution of the two-photon invariant mass in the $\eta$ region, at different stages of the selection, is shown in Fig. 2. The resolution on the $\eta$ invariant mass is 13 MeV/$c^2$. Candidates with invariant mass within 26 MeV/$c^2$ of the nominal $\eta$ mass $m_{\eta }$ [46] are selected for the signal sample, while those in the regions 39 MeV/$c^2$ $<|M(\gamma \gamma ) - m_{\eta }| < 52$ MeV/$c^2$ are used as control samples (sidebands). In both cases, we constrain the $\gamma \gamma$ invariant mass to the world-average $\eta$ mass to improve the resolution on the missing mass. To reduce QED backgrounds $e^+e^- \rightarrow (n\gamma ) + e^+e^-, \mu ^+\mu ^-,\tau ^+\tau ^-$, we apply the Belle standard selection for hadronic events [47] by requiring each event to have more than two charged tracks pointing towards the primary interaction vertex, a total visible energy greater than $0.2\sqrt{s}$ (where $\sqrt{s}$ is the center-of-mass energy of the $e^+e^-$ pair), a total energy deposit in the ECL between $0.1\sqrt{s}$ and $0.8\sqrt{s}$, and a total momentum balanced along the beam axis. Continuum $e^+e^- \rightarrow q\bar{q}$ events, which are the largest contributor to the background, are characterized by a distinct event topology and are suppressed with the requirement on the ratio of Fox–Wolfram moments $R_2 = H_2/H_0$ [48] to be less than 0.3. Fitting the $M(\gamma \gamma )$ distribution, we estimate the purity of the selected $\eta$ candidates to be $13\%$. The comparison between the MC simulation and the data is shown in Fig. 3. The MC simulation underestimates the number of events in the $\eta$ invariant mass window by a factor of 1.49, and does not accurately describe the shape of the distribution observed in the data. We attribute this effect to a non-optimal tuning of the Pythia6 parameters controlling the $SU(3)_{\mathrm {flavour}}$ breaking effects and the production rates of $\eta$ and $\eta ^{\prime }$ mesons.

Fig. 2

Two photon invariant mass at different stages of the $\eta$ selection, from the $\varUpsilon (5S)$ collison data: before the selection (black solid), after the photon selection (black hatched), and after all the selections, including the $\pi ^0$ veto (blue solid)

Fig. 3

Missing mass of the $\eta$ candidate after the selection. The distribution obtained in the data (red solid histogram) is compared with the MC expectation (black shaded histogram), rescaled by a factor 1.49. The binning shown here is 50 times larger than the one used in the fitting procedure

Fig. 4

$M_{\mathrm {miss}}(\eta )$ distribution after the subtraction of the fitted background component. The blue solid line shows the signal component of the global fitting function, while the red dashed line represents the background-only component. The binning shown here is 50 times larger than the one used in the fitting procedure

The signal transitions appear as narrow peaks in the $M_{\mathrm {miss}}(\gamma \gamma )$ distribution, whose widths are determined by the resolution on the photon energy reconstruction and the resolution on the beam energy, which is about 5 MeV. The resulting missing mass resolution decreases almost linearly with $M_{\mathrm {miss}}(\gamma \gamma )$, from 14.1 MeV/$c^2$ at $M_{\mathrm {miss}}(\gamma \gamma ) = m_{\varUpsilon (1S)}$ to 6.3 MeV/$c^2$ at $M_{\mathrm {miss}}(\gamma \gamma ) = m_{h_b(2P)}$. At

$M_{\mathrm {miss}}(\gamma \gamma ) = m_{\varUpsilon (1D)}$, the resolution is 7.6 MeV/$c^2$. The $\varUpsilon (nS)$ and $h_b(nP)$ signals probability density functions (PDFs) are modeled by Crystal Ball [49] whose resolutions are fixed to the MC simulation values. The non-Gaussian tail of this PDF captures the effects of the soft initial state radiation (ISR). A simulation method based on the next-to-leading order formula for the ISR emission probability [50] is used to determine the tail parameters of each signal PDF, which are fixed in the fit. For this calculation, we assume that the energy dependence of the signal cross section is described by a non-relativistic Breit-Wigner function with the parameters of the $\varUpsilon (5S)$ resonance [46]. The $\varUpsilon _J(1D)$ signal is comprised of three possible states, with unknown fractions and mass splittings. Therefore, we model its PDF as the sum of three separate Crystal Ball functions $\mathcal{C}_{J}(m_J)$ with the two scale factors $f_1$ and $f_3$ defined earlier:

$$\begin{aligned} \mathcal{F}_{1D} = \frac{N_{1D}}{1+f_1+f_3}\cdot [\mathcal{C}_{2}(m_{2}) + f_1 \mathcal{C}_{1}(m_1) + f_3 \mathcal{C}_{3}(m_3)], \end{aligned}$$

where $N_{1D}$ is the overall yield of $\varUpsilon _J(1D)$, $m_2$ is the $\varUpsilon _2(1D)$ mass and the $\varUpsilon _{1,3}(1D)$ masses are parametrized as $m_1 = m_2 - \varDelta M_{12}$ and $m_3 = m_2 + \varDelta M_{23}$, with $\varDelta M_{ij}$ representing the fine splitting between the $J=1,3$ and $J = 2$ members of the triplet. To ensure the convergence and stability of the fit, some of the $\mathcal{F}_{1D}$ parameters are fixed. Theoretical calculations [51,52,53,54,55,56,57,58] and experimental observations [59, 60] suggest that $\varDelta M_{ij} < 10$ MeV/$c^2$; therefore, we fix these to 5 MeV/$c^2$. Similarly $m_2$ is fixed to the world average value of $10163.7 \pm 1.4$ MeV/$c^2$ [46]. The parameters $f_1$, $f_3$ and $N_{1D}$ are allowed to vary. The fit is performed in a single region from 9.2 to 10.3 GeV/$c^2$ of the binned $M_{\mathrm {miss}}(\gamma \gamma )$ distribution, with a bin width of 0.1 MeV/$c^2$. The background is modeled with the sum of an ARGUS PDF [61] and a seventh-order polynomial. The cut-off parameter of the ARGUS PDF is fixed by the MC simulation, while all the other parameters are allowed to float. The order of the polynomial is chosen to maximize the fit probability. The result of the fit is shown in Fig. 4, where the background PDF has been subtracted to enhance the visibility of the signals. The fit has 17 free parameters ($f_1$ and $f_2$, 10 for the background shape and yield, and 5 signal yields) and a probability of $11\%$. The numerical results are summarized in Table 1. We observe the $e^+e^- \rightarrow \eta \varUpsilon _J(1D)$ process and provide evidence for $e^+e^- \rightarrow \eta \varUpsilon (2S)$. No significant $h_b(nP)$ nor $\varUpsilon (1S)$ signals are observed.

Table 1 Results of the fit of $M_{\mathrm {miss}}(\eta )$. Significance ($\varSigma$), measured signal yield ($N_{\mathrm {meas}}$), and $\varUpsilon _J(1D)$ triplet fractions are reported. The errors on $N_{\mathrm {meas}}$ and $f_J$ are statistical only, while the fit-related systematic uncertainties are taken into account in the significance estimation

We perform several cross-checks of the fit procedure. First, we verify that the polynomial component has no ripples nor local maxima in the signal regions by studying its first and second derivatives. The fit is then performed on both the MC background-only dataset and a subset of the real data in which the $\gamma \gamma$ pair belongs to the $\eta$ mass sidebands. In both cases, all the signal yields are compatible with zero and the background PDF properly describes the data shape, disfavoring the presence of unaccounted peaking backgrounds. Second, we test a few obvious alternative background models. We replace the ARGUS component with the missing-mass distribution obtained in the background-only MC, then we split the fit range into two sub-ranges above and below $M_{\mathrm {miss}} = 9.8$ GeV/$c^2$, and finally we remove completely the ARGUS component. In all cases, we cannot match the performance of the nominal model without introducing additional free parameters. With the first alternative, we obtain a fit probability of $1\%$ if we increase the polynomial order to 8. With the second alternative we obtain a $10\%$ probability in the upper range, using PDF with an eighth-order polynomial component, and a $5\%$ probability in the lower one using a third-order polynomial. The third alternative gives a $0.5\%$ fit probability when the polynomial order is increased to 15. We therefore do not regard these as credible alternative models to describe the data.

Table 2 Efficiency $\epsilon$, visible cross section $\sigma _v$, ISR correction factor $(1+\delta _{\mathrm {ISR}})$, and Born-level cross section $\sigma _B$ for the processes considered in this analysis. Upper limits are calculated at $90\%$ confidence level as described in the text

Table 3 Systematic uncertainties, in percentage, on the measurement of the Born-level cross sections of the $e^+e^- \rightarrow \eta b\bar{b}$ processes

The visible cross section $\sigma _{v}$ is calculated starting from the fitted yields as $\sigma _{v} = N_{\mathrm {meas}}/\epsilon \mathcal{B}[\eta \rightarrow \gamma \gamma ]\mathcal{L}$, where $N_{\mathrm {meas}}$ is the measured number of signal events, $\mathcal{L}$ is the integrated luminosity, and $\epsilon$ is the reconstruction efficiency. This quantity can be related to the Born cross section ($\sigma _B$) by de-convolving the ISR effects [50]:

$$\begin{aligned} \sigma _{v}(\sqrt{s}) = \frac{\int _{0}^{\frac{2E_{m}}{\sqrt{s}}} \sigma _{B}(x) W(\sqrt{s}, x) dx}{|1- \varPi |^2} = \sigma _{B}(\sqrt{s})\frac{1 + \delta _{\mathrm {ISR}}}{|1- \varPi |^2}, \end{aligned}$$

where $|1- \varPi |^2 = 0.929$ is the vacuum-polarization factor [33, 62], $(1 + \delta _{\mathrm {ISR}})$ is the ISR correction factor and x can be interpreted as the fractional energy lost to ISR radiation. The maximum radiated energy is related to the minimum invariant mass of the final hadronic state $M_{\mathrm {min}} = m_{\eta } + m_{(b\bar{b})}$, as $E_m = (s-M^2_{\mathrm {min}})/2\sqrt{s}$. To calculate the value of $(1+\delta _{\mathrm {ISR}})$, we assume that the Born cross section follows a non-relativistic Breit-Wigner shape, and we numerically integrate the expression above. To determine its uncertainty, we repeat the calculation several times, sampling randomly and simultaneously the $\varUpsilon (5S)$ parameters and the center of mass energy from Gaussian distributions. The uncertainty on the ISR correction factor is then determined by the spread in the distribution of the $(1 + \delta _{\mathrm {ISR}})$ values. In the process, we assume no correlation among the $\varUpsilon (5S)$ mass and width uncertainties.

A summary of the results, including the values of $(1+\delta _{\mathrm {ISR}})$, is presented in Table 2. To evaluate the upper limits (UL), we use the CL$_s$ modified frequentist method [63] with the profile likelihood ratio as the test statistic. Systematic uncertainties are included by the generation of pseudo-experiments. The significances reported in Table 1 are evaluated using the asymptotic formulae for the profile likelihood ratio, treating the fit-related systematic uncertainties by including an extra nuisance parameter [64]. To perform the fits and the statistical analysis, we use the RooFit [65] and RooStats [66] packages.

We investigate several sources of systematic uncertainty, as summarized in Table 3. The luminosity collected at the $\varUpsilon (5S)$ energy has been measured with an uncertainty of $1.4\%$. The reconstruction efficiency includes several contributions. The photon reconstruction efficiency is known with a $\pm \,2.8\%$ uncertainty per photon, corresponding to $\pm \,5.6\%$ per $\eta$, and has been estimated using $D \rightarrow K^{\pm }\pi ^{\mp }\pi ^{0}$ events. The uncertainty arising from the continuum rejection procedure is estimated to be $3.5\%$ by selecting $e^+e^- \rightarrow \pi ^+\pi ^- \varUpsilon (2S)$ events and comparing the efficiency of the continuum suppression measured in the data with the one expected from the MC simulation [29]. The uncertainty due to the photon energy calibration affects both the signal resolution and the $\eta$ invariant-mass selection. To estimate these effects, we repeat the analysis while varying the calibration factors within their errors. The background-related uncertainty is obtained by changing simultaneously the polynomial order between 5 and 9, the lower fit-range edge between 9.1 and 9.3 GeV, the upper edge between 10.27 and 10.31 GeV and the bin width between 0.1 and 0.5 MeV. The standard deviation of the distribution of the fit results is then used as the systematic uncertainty. The signal model uncertainty is related to the choice of the fixed parameters of the fit. The masses of $\varUpsilon (1S,2S)$ and $h_{b}(1P,2P)$ are varied within their uncertainties and the fit is repeated, obtaining a fluctuation in the signal yields from 2.5 to $5.5\%$, depending on the channel. For the $\varUpsilon _J(1D)$, we repeat the fit, changing both the $\varUpsilon _J(1D)$ mass within its uncertainties and the values of the splittings between 2 and 15 MeV/c${^2}$. To account for possible correlations, we vary all these three parameters independently and simultaneously, repeating the fit under 1960 different configurations. Also, in this case, the standard deviation of the fit result is assumed as a systematic uncertainty. The $(1+ \delta _{\mathrm {ISR}})$ factor is calculated with a $\approx 1\%$ precision, according to the channel. Nevertheless, the same parameters that determine the error on $(1+ \delta _{\mathrm {ISR}})$ are also responsible for the uncertainty on the radiative tail in the signal PDF. To estimate the global ISR-related uncertainty, we randomly sample the $\varUpsilon (5S)$ parameters and the beam energy as previously described. For each set of parameters, we calculate the ISR correction factor and the signal fit parameters, and then repeat the fit. We find a strong anti-correlation between the fitted signal yields and $1/(1+\delta _{\mathrm {ISR}})$, which means that most of the uncertainty cancels out, leaving only a residual uncertainty of $\approx 0.6\%$. Finally, we include an uncertainty arising from the precision of the world-average value of the $\eta \rightarrow \gamma \gamma$ branching fraction [46].

The behaviour of the hadronic cross section in the $\varUpsilon (5S)$ region is not yet entirely understood [67]. However, assuming that a process proceeds entirely through the $\varUpsilon (5S)$ (i.e., there is no continuum contribution, as we assume for the calculation of the ISR correction factor), and that $\sigma [e^+e^- \rightarrow \varUpsilon (5S)] = \sigma [e^+e^- \rightarrow b \bar{b}] = (0.340 \pm 0.016)$ nb [68], an estimation of the branching fraction can be obtained from the visible cross section with the formula $\mathcal{B}[\varUpsilon (5S) \rightarrow \eta X] = \sigma _v[e^+e^- \rightarrow \eta X] / \sigma [e^+e^- \rightarrow b \bar{b}].$ Under these assumptions, we calculate the branching fraction $\mathcal{B}[\varUpsilon (5S) \rightarrow \eta \varUpsilon _J(1D)] = (4.82 \pm 0.92 \pm 0.67) \times 10^{-3}$. Theoretical calculations that account for the effect of virtual B meson loops are in agreement with our result [37].

Our measurements of $f_1$ and $f_3$, the fraction of transitions to $\varUpsilon _J(1D)$ that produce the $J=1$ and $J=3$ members of the triplet, respectively, with $\varDelta M_{ij} = 5$ MeV/$c^2$, are both compatible with 0. We repeat the fit for other values of the fine splittings in the favoured range of 3 to 15 MeV/$c^2$ and, again, do not find significant signals of $J=1$ or $J=3$ states. Possible explanations are that either $\varDelta M_{12}$ and $\varDelta M_{23}$ are comparable within our experimental resolution, as previous analyses and theoretical predictions suggest, or the $\eta$ transition preferentially produces only one member of the triplet, or both. We set $90\%$ confidence level (C.L.) upper limits on $f_1$ and $f_3$ as function of $\varDelta M_{12}$ and $\varDelta M_{23}$, as shown in Fig. 5 and 6. The predictions [37] for $f_1$, namely $f_1 = 0.65$, exclude the region where $\varDelta M_{23} \lesssim 7$ MeV/$c^2$ and $\varDelta M_{12} \gtrsim 14$ MeV/$c^2$ (Fig. 5), while the predictions for $f_3$ provide no constraint on either quantity (Fig. 6).

Fig. 5

$90\%$ C.L. upper limit on $f_1$, as function of the chosen $\varUpsilon _J(1D)$ fine splitting values. The black lines represent the curves at fixed values of the UL in steps of 0.5. The corresponding UL value is reported next to each line. Dashed and solid line styles are alternated for clarity. The thick gray dashed line demarcates the region excluded by the theoretically-favored value $f_1 = 0.68$ [37]

Fig. 6

$90\%$ C.L. upper limit on $f_3$, as function of the chosen $\varUpsilon _J(1D)$ fine splitting values. The black lines represent the curves at fixed values of the UL in steps of 0.5. The corresponding UL value is reported next to each line. Dashed and solid line styles are alternated for clarity

In summary, we report here the first observation of the process $e^+e^- \rightarrow \eta \, \varUpsilon _J(1D)$ and the first search for $e^+e^- \rightarrow \eta h_b(1P, 2P)$ in the vicinity of the $\varUpsilon (5S)$ resonance. The measured visible cross section at $\sqrt{s} = 10.865$ GeV for the former process is $\sigma _{v}[e^+e^- \rightarrow \eta \varUpsilon _J(1D)] = (1.14 \pm 0.22 \pm 0.15)$ pb. Taking into account the radiative corrections, we measure the Born-level cross section $\sigma _{B}[e^+e^- \rightarrow \eta \varUpsilon _J(1D)] = (1.64 \pm 0.31 \pm 0.21)$ pb. We also find evidence for the process $e^+e^- \rightarrow \eta \varUpsilon (2S)$ and we measure the cross section $\sigma _{v}[e^+e^- \rightarrow \eta \varUpsilon (2S)] = (0.70 \pm 0.21 \pm 0.12)$ pb, corresponding to $\sigma _{B}[e^+e^- \rightarrow \eta \varUpsilon (2S)] = (1.02 \pm 0.30 \pm 0.17)$ pb. We do not have significant evidence of $e^+e^- \rightarrow \eta h_b(1P, 2P)$ nor $e^+e^- \rightarrow \eta \varUpsilon (1S)$. A much larger statistics data set, like the one obtainable with the Belle II experiment [69], is needed to perform such measurements. We do not have direct evidence of the presence of the three states of the $\varUpsilon _J(1D)$ triplet, and we derive $90\%$ CL upper limits on the fraction of the $J=1$ and $J=3$ state with respect to the $J=2$ state. Our results for the $e^+e^- \rightarrow \eta \varUpsilon (nS)$ process agree with a preliminary Belle study in which the exclusive reconstruction of $\varUpsilon (1S, 2S)$ into lepton pairs was used [36].

We thank the KEKB group for the excellent operation of the accelerator; the KEK cryogenics group for the efficient operation of the solenoid; and the KEK computer group, the National Institute of Informatics, and the PNNL/EMSL computing group for valuable computing and SINET5 network support. We acknowledge support from the Ministry of Education, Culture, Sports, Science, and Technology (MEXT) of Japan, the Japan Society for the Promotion of Science (JSPS), and the Tau-Lepton Physics Research Center of Nagoya University; the Australian Research Council; Austrian Science Fund under Grant No. P 26794-N20; the National Natural Science Foundation of China under Contracts No. 10575109, No. 10775142, No. 10875115, No. 11175187, No. 11475187, No. 11521505 and No. 11575017; the Chinese Academy of Science Center for Excellence in Particle Physics; the Ministry of Education, Youth and Sports of the Czech Republic under Contract No. LTT17020; the Carl Zeiss Foundation, the Deutsche Forschungsgemeinschaft, the Excellence Cluster Universe, and the VolkswagenStiftung; the Department of Science and Technology of India; the Istituto Nazionale di Fisica Nucleare of Italy; the WCU program of the Ministry of Education, National Research Foundation (NRF) of Korea Grants No. 2011-0029457, No. 2012-0008143, No. 2014R1A2A2A01005286,

No. 2014R1A2A2A01002734,

No. 2015R1A2A2A01003280, No. 2015H1A2A1033649, No. 2016R1D1A1B01010135, No. 2016K1A3A7A09005603, No. 2016K1A3A7A09005604, No. 2016R1D1A1B02012900, No. 2016K1A3A7A09005606,

No. NRF-2013K1A3A7A06056592; the Brain Korea 21-Plus program, Radiation Science Research Institute, Foreign Large-size Research Facility Application Supporting project and the Global Science Experimental Data Hub Center of the Korea Institute of Science and Technology Information; the Polish Ministry of Science and Higher Education and the National Science Center; the Ministry of Education and Science of the Russian Federation under contract 14.W03.31.0026, the Slovenian Research Agency; Ikerbasque, Basque Foundation for Science and the Euskal Herriko Unibertsitatea (UPV/EHU) under program UFI 11/55 (Spain); the Swiss National Science Foundation; the Ministry of Education and the Ministry of Science and Technology of Taiwan; and the U.S. Department of Energy and the National Science Foundation.