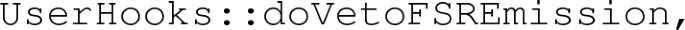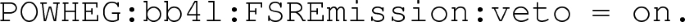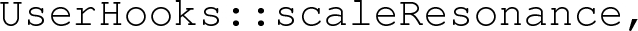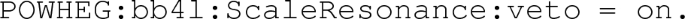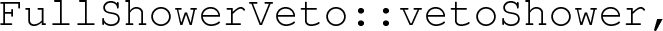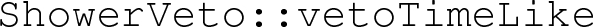Abstract
In this paper we study the theoretical uncertainties in the determination of the top-quark mass using next-to-leading-order (NLO) generators interfaced to parton showers (PS) that have different levels of accuracy. Specifically we consider three generators: one that implements NLO corrections in the production dynamics, one that includes also NLO corrections in top decay in the narrow width approximation, and one that implements NLO corrections for both production and decay including finite-width and interference effects. Since our aim is to provide an assessment of the uncertainties of purely theoretical origin, we consider simplified top-mass related observables that are broadly related to those effectively used by experiments, eventually modelling experimental resolution effects with simple smearing procedures. We estimate the differences in the value of the extracted top mass that would occur due to the use of the three different NLO generators, to the variation of scales, to the choice of parton distribution functions and to the matching procedure. Furthermore, we also consider differences due to the shower and to the modelling of non-perturbative effects by interfacing our NLO generators to both Pythia8.2 and Herwig7.1, with various settings. We find very different results depending upon the adopted shower model. While with Pythia8.2 we find moderate differences between the different NLO+PS generators, with Herwig7.1 we find very large ones. Furthermore, the differences between Pythia8.2 and Herwig7.1 generators are also remarkably large.
Similar content being viewed by others
1 Introduction
The abundant production of top pairs at the Large Hadron Collider (LHC) provides an opportunity for detailed studies of top-quark properties, for tests of the Standard Model (SM) in the top sector, and for measurements of fundamental parameters such as the top-quark mass. With the Higgs boson mass now known with high precision, the W-boson and top-quark masses have become strongly correlated, and an accurate determination of both would lead to a SM test of unprecedented precision [1, 2]. The present value of the indirect top-mass determination from electroweak precision data (\(176.7\pm 2.1\) GeV, see [1]) is in slight tension, at the \(1.6\,\sigma \) level, with the direct measurements. The latest combination of the Tevatron and the LHC results [3] yields \(173.34\pm 0.76\) GeV, but more recent results favour even smaller values, close to 172.5 GeV, see [4,5,6,7]. Recent reviews of top-mass measurements by the ATLAS and CMS collaborations can be found in Refs. [8, 9].
It has been shown that in the Standard Model as is (i.e. assuming no new physics effects up to the Planck scale), the vacuum is stable if the top mass, \(m_{t}\), is below 171 GeV (i.e. very close to its present value), metastable up to 176 GeV, and unstable above this value [10,11,12,13]. The current value is safely below the instability region. However, it should not be forgotten that the absence of new physics up to the Planck scale is a very strong assumption. The only conclusion we can draw from these results is that there is no indication of new physics below the Planck scale coming from the requirement of vacuum stability. On the other hand, the fact that the Higgs boson quartic coupling almost vanishes at the Planck scale may have some deep meaning that we are as yet unable to unveil.
Besides the issues related to electroweak tests and the stability of the vacuum, the question on how precisely we can measure the top mass at hadron colliders also has its own significance, related to our understanding of QCD and collider physics. In view of the large abundance of top-pair production at the LHC, it is likely that precise measurements will be performed with very different methods, and that comparing them will give us confidence in our ability to handle hadron-collider physics problems.
Top-mass measurements are generally performed by fitting \(m_{t}\)-dependent kinematic distributions to Monte Carlo predictions. The most precise ones, generally called direct measurements, rely upon the full or partial reconstruction of the system of the top-decay products. The ATLAS and CMS measurements of Refs. [4, 5], yielding the value \(172.84 \pm 0.34~{\mathrm{(stat)}} \pm 0.61\) (syst) GeV and \(m_{t}=172.44 \pm 0.13~{\mathrm{(stat)}} \pm 0.47\) (syst) GeV respectively, fall into this broad category.
The top mass cannot be defined in terms of the mass distribution of the system of its decay products: since the top quark is a coloured object, no final-state particle system can be unambiguously associated with it. On the other hand, the top mass is certainly related to the mass distribution of the system of objects arising from top decay, i.e. hard leptons, neutrinos and hard, b-flavoured hadronic jets. The mass distribution of this system can be computed and measured, and the top mass enters this computation as a parameter. By extracting its value from a fit to the measured distributions, we are unavoidably affected by theoretical errors that must be carefully assessed. In particular, these errors will depend upon the accuracy of the modelling of these distributions.
The absence of a “particle truth level” for the top-decay products has led to speculations that the top mass cannot be extracted reliably in the direct measurements. The extracted mass is unavoidably a parameter in the theoretical calculation or in the Monte Carlo generator that is used to compute the relevant distributions. It has thus been argued that, because of this, and since shower Monte Carlo (SMC) models are accurate at leading order (LO) only, the extracted mass cannot be identified with a theoretically well-defined mass, such as the pole mass or the \(\overline{\mathrm{MS}}\) mass (that differ among each other only at the NLO level and beyond).
In the present work, we use NLO-accurate generators, so that the previously mentioned objection does not actually apply. Moreover, it can be argued that, in the narrow width approximation and at the perturbative level, the mass implemented in Monte Carlo generators corresponds to the pole mass [14] even if we do not use NLO-accurate generators.
It was also argued in Ref. [15] that the Monte Carlo mass parameter differs from the top pole mass by an amount of the order of a typical hadronic scale, that was there quantified to be near 1 GeV. It was further argued that this difference is, in fact, intrinsic in the uncertainty with which the pole mass can even be defined, because of the presence of a renormalon in the relation of the pole to the \(\overline{\mathrm{MS}}\) mass [16, 17].
Recent studies [18, 19] have shown that the renormalon ambiguity in the top-mass definition is not as large as previously anticipated, being in fact well below the current experimental error.Footnote 1 The fact remains, however, that non-perturbative corrections to top-mass observables (not necessarily related to the mass renormalon) are present, can affect a top-mass determination, and are likely to be parametrically of the order of a typical hadronic scale. We believe, however, that this does not justify the introduction of a “Monte Carlo mass” concept, since it is unlikely that non-perturbative effects, affecting top-mass observables, can be parametrized as a universal shift of the top-mass parameter. The real question to answer is whether these non-perturbative effects are of the order of 100 MeV, 1 GeV, or more. While a top-mass determination from threshold production at an \(e^+e^-\) collider would be free of such uncertainties [22, 23],Footnote 2 at hadron colliders, non-perturbative effects of this order are likely to affect, to some extent, most top-mass observables that have been proposed so far.Footnote 3
The theoretical problems raised upon the top-quark mass measurement issues have induced several theorists to study and propose alternative methods. The total cross section for \(t\bar{t}\) production is sensitive to the top mass, and has been computed up to the NNLO order in QCD [25], and can be used to extract a top mass value [26,27,28].
In Ref. [29], observables related to the \(t{\bar{t}}+{\mathrm{jet}}\) kinematics are considered. The authors of Ref. [30] presented a method based upon the charged-lepton energy spectrum, that is not sensitive to top production kinematics, but only to top decay, arguing that, since this has been computed at NNLO accuracy [31, 32], a very accurate measurement may be achieved. Some authors have advocated the use of boosted top jets (see Ref. [33] and references therein). In Ref. [34], the authors make use of the \(b\)-jet energy peak position, that is claimed to have a reduced sensitivity to production dynamics. In Ref. [35], the use of lowest Mellin moments of lepton kinematic distributions is discussed. In the leptonic channel, it is also possible to use distributions based on the “stransverse” mass variable [36], which generalizes the concept of transverse mass for a system with two identical decay branches [37, 38].
Some of these methods have in fact been exploited [36, 39,40,41,42] to yield alternative determinations of \(m_{t}\). It turns out, however, that the direct methods yield smaller errors at the moment, and it is likely that alternative methods, when reaching the same precision level, will face similar theoretical problems.
1.1 Goals of this work
In this work, we exploit the availability of the new POWHEG BOX [43,44,45] generators for top-pair production, i.e. the \(t\bar{t}dec\) [46] and \(b\bar{b}4\ell \) [47] ones, in order to perform a theoretical study of uncertainties in the top-mass determination. In particular, we are in a position to assess whether NLO corrections in top decay, that are implemented in both the \(t\bar{t}dec\) and \(b\bar{b}4\ell \) generators, and finite width effects, non-resonant contributions and interference of radiation generated in production and decay, that are implemented in \(b\bar{b}4\ell \), can lead to sizeable corrections to the extracted value of the top mass. Since the \(hvq\) generator [48], that implements NLO corrections only in production, is widely used by the experimental collaborations in top-mass analyses, we are particularly interested in comparing it with the new generators, and in assessing to what extent it is compatible with them.Footnote 4 We will consider variations in the scales, parton distribution functions (PDFs) and the jet radius parameter to better assess the level of compatibility of the different generators.
We are especially interested in effects that can be important in the top-mass determination performed in direct measurements. Thus, the main focus of our work is upon the mass of a reconstructed top, that we define as a system comprising a hard lepton, a hard neutrino and a hard b jet. We will assume that we have access to the particle truth level, i.e. that we can also access the flavour of the b jet, and the neutrino momentum and flavour. We are first of all interested in understanding to what extent the mass peak of the reconstructed top depends upon the chosen NLO+PS generator. This would be evidence that the new features introduced in the most recent generators are mandatory for an accurate mass extraction.
We will also consider the inclusion of detector effects in the form of a smearing function applied to our results. Although this procedure is quite crude, it gives a rough indication of whether the overall description of the process, also outside of the reconstructed resonance peak, affects the measurement.
Besides studying different NLO+PS generators, we have also attempted to give a first assessment of ambiguities associated with shower and non-perturbative effects, by interfacing our NLO+PS generators to two shower Monte Carlo programs: Pythia8.2 [49] and Herwig7.1 [50, 51]. Our work focuses upon NLO+PS and shower matching. We thus did not consider further variations of parameters and options within the same parton shower, nor variations on the observables aimed at reducing the dependence upon those.Footnote 5
We have also considered two alternative proposals for top-mass measurements: the position of the peak in the b-jet energy [34] and the leptonic observables of Ref. [35]. The first proposal is an example of a hadronic observable that should be relatively insensitive to the production mechanism, but may be strongly affected by NLO corrections in decay. The second proposal is an example of observables that depend only upon the lepton kinematics, and that also depend upon production dynamics, thus stronger sensitivity to scale variations and PDFs may be expected. It is also generally assumed that leptonic observables should be insensitive to the b-jet modeling. One should remember, however, that jet dynamics affects lepton momenta via recoil effects, so it is interesting to study whether there is any ground to this assumption.
The impact of NLO corrections in decays and finite-width effects were also considered in Ref. [55] for a number of top-mass related observables, and in Ref. [56] for the method relying upon the \(t\bar{t}j\) final state. Here we are more interested in observables related to direct measurements, that are not considered there. Furthermore, we focus our studies upon the differences with respect to the widely-used \(hvq\) generator.
1.2 Preamble
The study presented in this work was triggered by the availability of new NLO+PS generators describing top decay with increasing accuracy. As such, its initial aim was to determine whether and to what extent these new generators, and the associated new effects that they implement, may impact present top-mass measurements. As we will see, had we limited ourselves to the study of the NLO+PS generators interfaced to Pythia8.2, we would have found a fairly consistent picture and a rather simple answer to this question.
Since another modern shower generator that can be interfaced to our NLO+PS calculation is available, namely Herwig7.1, we have developed an appropriate interface to it, and have also carried out our study using it as our shower model. Our results with Herwig7.1 turn out to be quite different from the Pythia8.2 ones, to the point of drastically altering the conclusions of our study. In fact, variations in the extracted top mass values due to switching between Pythia8.2 and Herwig7.1 prevail over all variations that can be obtained within Pythia8.2 by switching among different NLO+PS generators, or by varying scales and matching parameters within them. Moreover, the comparison of the various NLO+PS generators, when using Herwig7.1, does not display the same degree of consistency that we find within Pythia8.2. If, as it seems, the differences found between Pythia8.2 and Herwig7.1 are due to the different shower models (the former being a dipole shower, and the latter an angular-ordered one), the very minimal message that can be drawn from our work is that, in order to assess a meaningful theoretical error in top-mass measurements, the use of different shower models, associated with different NLO+PS generators, is mandatory.
Our results are collected in tables and figures that are presented and discussed by giving all details that are necessary to reproduce them. We present a large number of results that show the effect of changing parameter settings and matching methods in the NLO+PS calculations, some of which are very technical. Since this may obscure the logical development of our work, we have written our Summary (Sect. 9) in such a way that the main logical developments and findings are presented in a concise way. In fact, the summary section can be read independently of the rest of the paper, and may be used to navigate the reader through the rest of the material.
1.3 Outline
The paper is organized as follows. In Sect. 2 we briefly review the features of the \(hvq\), \(t\bar{t}dec\) and \(b\bar{b}4\ell \) generators. We also discuss the interfaces to the parton-shower programs Pythia8.2 and Herwig7.1.
In Sect. 3, we detail the setup employed for the phenomenological studies presented in the subsequent sections.
In Sect. 4, we perform a generic study of the differences of our generators focusing upon the mass distribution of the \(W\, b\)-jet system. The aim of this section is to show how this distribution is affected by the different components of the generators by examining results at the Born level, after the inclusion of NLO corrections, after the parton shower, and at the hadron level.
In Sect. 5 we describe how we relate the computed value of our observables to the corresponding value of the top mass that would be extracted in a measurement.
In Sect. 6 we consider as our top-mass sensitive observable the peak position in the mass distribution of the reconstructed top, defined as the mass of the system comprising the hardest lepton and neutrino, and the jet with the hardest b-flavoured hadron, all of them with the appropriate flavour to match a t or a \(\bar{t}\). We study its dependence upon the NLO+PS generator being used, the scale choices, the PDFs, the value of \(\alpha _{\mathrm{S}}\) and the jet radius parameter. Furthermore, we present and compare results obtained with the two shower Monte Carlo generators Pythia8.2 and Herwig7.1.
We repeat these studies for the peak of the b-jet energy spectrum [34] in Sect. 7, and for the leptonic observables [35] in Sect. 8.
In Sect. 9 we summarize our results, and in Sect. 10 we present our conclusions. In the appendices we give some technical details.
2 NLO+PS generators
In this section we summarize the features of the POWHEG BOX generators used in the present work, i.e. the \(hvq\), the \(t\bar{t}dec\) and the \(b\bar{b}4\ell \) generators.
The \(hvq\) program [48] was the first top-pair production generator implemented in POWHEG. It uses on-shell matrix elements for NLO production of \(t\bar{t}\) pairs. Off-shell effects and top decays, including spin correlations, are introduced in an approximate way, according to the method presented in Ref. [57]. Radiation in decays is fully handled by the parton-shower generators. The ones that we consider, Pythia8.2 and Herwig7.1, implement internally matrix-element corrections for top decays, with Herwig7.1 also optionally including a POWHEG-style hardest-radiation generation. In these cases, their accuracy in the description of top decays is, for our purposes, equivalent to the NLO level.
The \(t\bar{t}dec\) code [46] implements full spin correlations and NLO corrections in production and decay in the narrow-width approximation. Off-shell effects are implemented via a reweighting method, such that the LO cross section includes them exactly. As such, it also contains contributions of associated top-quark and W-boson production at LO. It does not include, however, interference of radiation generated in production and decay.
In \(t\bar{t}dec\) the POWHEG method has been adapted to deal with radiation in resonance decays. Radiation is generated according to the POWHEG Sudakov form factor both for the production and for all resonance decays that involve coloured partons. This feature also offers the opportunity to modify the standard POWHEG single-radiation approach. Rather than picking the hardest radiation from one of all possible origins (i.e. production and resonance decays), the POWHEG BOX can generate simultaneously the hardest radiation in production and in each resonance decay. The LH events generated in this way can thus carry more radiated partons, one for production and one for each resonance. Multiple-radiation events have to be completed by a shower Monte Carlo program, that has to generate radiation from each origin without exceeding the hardness of the corresponding POWHEG one, thus requiring an interface that goes beyond the simple Les Houches standard [58].
A general procedure for dealing with decaying resonances that can radiate by strong interactions has been introduced and implemented in a fully general and automatic way in a new version of the POWHEG BOX code, the POWHEG BOX RES [59]. This framework allows for the treatment of off-shell effects, non-resonant subprocesses including full interference, and for the treatment of interference of radiation generated in production and resonance decay.Footnote 6 In Ref. [47] an automated interface of the POWHEG BOX RES code to the OpenLoops [61] matrix-element generator has been developed and used to build the \(b\bar{b}4\ell \) generator, that implements the process \(pp\rightarrow b\bar{b}\,e^+\nu _{e}\, \mu ^-\bar{\nu }_{\mu }\), including all QCD NLO corrections in the 4-flavour scheme, i.e. accounting for finite b-mass effects. So, double-top, single-top and non-resonantFootnote 7 diagrams are all included with full spin-correlation effects, radiation in production and decays, and their interference.
As for the \(t\bar{t}dec\) generator, \(b\bar{b}4\ell \) can generate LH events including simultaneous radiation from the production process and from the top and anti-top decaying resonances. It thus requires a non-standard interface to parton-shower Monte Carlo programs, as for the case of the \(t\bar{t}dec\) generator.
2.1 Interface to shower generators
According to the POWHEG method, the PS program must complete the event only with radiation softer than the POWHEG generated one. In the standard Les Houches Interface for User Processes (LHIUP) [58], each generated event has a hardness parameter associated with it, called scalup. This parameter is set in POWHEG to the relative transverse momentum of the generated radiation and each emission attached by the parton shower must have a \(p_{T} \) smaller than its value. The LHIUP treats all emissions on an equal footing, and has no provision for handling radiation from decaying resonances. This drives a standard PS to allow showering to start from scales of the order of the resonance mass.
2.1.1 Generic method
References [46, 47] introduce a generic method for interfacing POWHEG processes that include radiation in decaying resonances with PS generators. According to this method, shower radiation from the resonance is left unrestricted, and a veto is applied a posteriori: if any radiation in the decaying resonance shower is harder than the POWHEG generated one, the event is discarded, and the same LH event is showered again. We also stress that the standard PS implementations conventionally preserve the mass of the resonance, as long as the resonance decay products, including eventually the radiation in decay, have the resonance as mother particle in the LH event record.
The hardness of the radiation associated with the decaying top (\(t\rightarrow W\,b\,g\)) in POWHEG is given by
where \(p_{g/b}\) and \(E_{g/b}\) are the four momentum and energy of the gluon and of the bottom quark, \(\beta _b\) is the velocity of the bottom quark and \(\theta _{bg}\) is the angle between the bottom and gluon momenta, all evaluated in the top rest frame. This hardness definition is internally used to define the corresponding Sudakov form factor. The same should be also used to limit the transverse momentum generated by the PS in the resonance decay.
The practical implementation of the veto procedure depends on whether we are using a dipole, as in Pythia8.2, or an angular-ordered shower, as in Herwig7.1. If we are using a dipole (\(p_{T} \)-ordered) shower, it is sufficient to check the first shower-generated emission from the bottom quark and (if present at the LH level) from the gluon arising in top decay. The hardness \(t_b\) of the shower-generated emission from the bottom is evaluated using Eq. (1), while the one from the gluon is taken to be
where \(E_{1,2}\) are the energies of the two gluons arising from the splitting, and \(\theta _{12}\) is the angle between them. Both \(t_g\) and \(t_b\) are computed in the top frame. If they are smaller than t, the event is accepted, otherwise it is showered again.
In the case of angular-ordered showers, as in Herwig7.1, it is not enough to examine the first emission, because the hardest radiation may take place later. As shown in Ref. [43], in the leading logarithmic approximation, the hardest emission in an angular-ordered shower can be always found by following either the quark line in a \(q \rightarrow q g\) splitting, or the most energetic line in a \(g \rightarrow gg\) splitting. Thus, when inspecting the sequence of splittings, in order to find the hardest radiation, if the parton that generates the shower is a fermion (in our case, the \(b/\bar{b}\) quark), we simply follow the fermionic line; in case of a gluon splitting, we follow the most energetic gluon. We go on until either the shower ends, or we reach a \(g\rightarrow q \bar{q}\) splitting. Since this last process is not soft-singular, configurations with the hardest emission arising after it are suppressed.
2.1.2 Standalone implementations in Pythia8.2
The Pythia8.2 generator provides facilities for implementing the above-described method to internally veto radiation in resonance decays. We prepared two implementations, each based on a different facility, and now we describe them in turn.
-
1.
At every radiation generated by Pythia8.2, a function is called internally using the UserHooks facility. The function inspects the radiation kinematics. If the radiation comes from top decays, it computes its transverse momentum, according to Eqs. (1) and (2). If the transverse momentum is larger than the one of the radiation generated by POWHEG in the resonance decay, the emission is vetoed, and Pythia8.2 tries to generate another splitting. The process is repeated until an acceptable splitting is generated. This behaviour is achieved by implementing the method
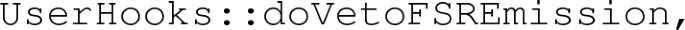
whose description can be found in the Pythia8.2 manual [62]. It is activated by setting the Pythia8.2 flag
-
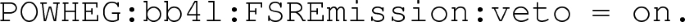
2.
The UserHooks facility also allows us to set the initial scale of final-state shower evolution (for the shower arising from the decaying resonances) equal to the transverse momentum of the top radiation in decay. This is achieved using the method
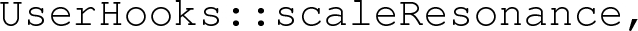
and is activated by setting the Pythia8.2 flag
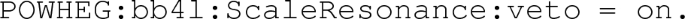
This method has the disadvantage of relying upon the assumption that the hardness definition used by Pythia8.2 is compatible with the POWHEG one.
Both methods are implemented in the file
in the \(b\bar{b}4\ell \) subprocess directory.
We have chosen implementation 1 as our default, and compared it with the other implementations in order to validate it and estimate matching uncertainties.
2.1.3 Standalone implementations in Herwig7.1
Also in the case of Herwig7.1 we have prepared two implementations that use the MC internal facilities to perform the veto:
-
1.
After the whole time-like shower has been developed, but before hadronization has been carried out, the showers from the b and from the POWHEG radiated gluon in top decay are examined. In the case of the b, the quark line is followed, and the transverse momentum of the radiation is computed (in the top frame) according to Eq. (1). In the case of the gluon, the hardest line is followed, and the transverse momentum of the radiation is computed according to Eq. (2). If a radiation is found with transverse momentum harder than the POWHEG generated one, the full event is reshowered, starting from the same LH event. The corresponding method is called
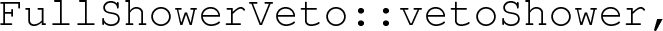
and we have implemented it in the files
-
2.
We veto each radiation in resonance decay if its transverse momentum is harder than the POWHEG generated one. In this case, Herwig7.1 tries again to generate radiation starting from the (angular ordering) hardness parameter of the vetoed one. As in Pythia8.2 second method, we have to rely in this case upon the Herwig7.1 definition of the radiation transverse momentum. The corresponding method is called
and we implemented it in the files
We will adopt implementation 2 as our Herwig7.1 default, and compare with the other one in order to validate it, and also in order to get an indication of the size of matching uncertainties.
3 Phenomenological analysis setup
We simulate the process \(p\,p \rightarrow b\, \bar{b}\,e^+\nu _{e}\, \mu ^-\bar{\nu }_{\mu }\), which is available in all three generators. It is dominated by top-pair production, with a smaller contribution of Wt topologies. For the observables we consider, the decay of one of the two top quarks is mostly irrelevant, so that our result will also hold for semileptonic decays.
In the \(hvq\) and \(t\bar{t}dec\) generators we renormalize the top mass in the pole-mass scheme, while in the \(b\bar{b}4\ell \) one we adopt the complex mass scheme [47], with the complex mass defined as \(\sqrt{m_{t}^2-i\,m_{t}\,\Gamma _t}\).
We perform our simulations for a center-of-mass energy of \(\sqrt{s}=8\) TeV. We have used the MSTW2008nlo68cl PDF set [63] and we have chosen as central renormalization and factorization scale (\(\mu _{\mathrm {R}}\) and \(\mu _{\mathrm {F}}\)) the quantity \(\mu \), defined, following Ref. [47], as the geometric average of the transverse masses of the top and anti-top
where the top and anti-top energies \(E_{t/\bar{t}}\) and longitudinal momenta \(p_{z,t/\bar{t}}\) are evaluated at the underlying-Born level.
In the \(b\bar{b}4\ell \) case, there is a tiny component of the cross section given by the topology
In this case we define \(\mu \) as
where \(p_{Z}=p_{\mu ^-}+p_{\bar{\nu }_\mu } + p_{e^+} +p_{\nu _{e}}\). This case is however very rare and unlikely to have any significance.
The parameter hdamp controls the separation of remnants (see “Appendix A”) in the production of \(t\bar{t}\) pairs with large transverse momentum. We set it to the value of the top mass.
3.1 Physics objects
In our simulations we make the B hadrons stable, in order to simplify the definitions of b jets. Jets are reconstructed using the Fastjet [64] implementation of the anti-\(k_{\mathrm{T}}\) algorithm [65] with \(R=0.5\). We denote as B (\({\bar{B}}\)) the hardest (i.e. largest \(p_{\mathrm{T}}\)) b (\(\bar{b}\)) flavoured hadron. The b (\(\bar{b}\)) jet is the jet that contains the hardest B (\(\bar{B}\)).Footnote 8 It will be indicated as \(j_B\) (\(j_{\bar{B}}\)). We discard events where the b jet and \(\bar{b}\) jet coincide. The hardest \(e^+\) (\(\mu ^-\)) and the hardest \(\nu _e\) (\(\bar{\nu }_{\mu }\)) are paired to reconstruct the \(W^+\) (\(W^-\)). The reconstructed top (anti-top) quark is identified with the corresponding \(W^+j_B\) (\(W^-j_{\bar{B}}\)) pair. In the following we will refer to the mass of this system as \(m_{Wb_j}\).
We require the two b jets to have
These cuts suppress the single-top topologies. The hardest \(e^+\) and the hardest \(\mu ^-\) must satisfy
3.2 Generated sample
For each generator under study, we have produced three samples of events, each sample computed with a top mass of 169.5, 172.5 and 175.5 GeV, respectively, with the corresponding decay width computed at NLO. Using the reweighting feature of the POWHEG BOX, we have computed the event weights obtained by varying the parton distribution functions and the renormalization and factorization scales, for a total of 12 weights (see Sects. 6.1.1 and 6.1.2 for more details).
In the reweighting procedure, only the inclusive POWHEG cross section is recomputed. The Sudakov form factor is not recomputed, so that the radiated partons retain the same kinematics. For this reason, the change of the renormalization and factorization scales do not affect the emission of radiation. Thus, in order to investigate the sensitivity of the result on the intensity of radiation, where we are particularly concerned with emissions from the final-state b quarks, we have also generated samples with the NPDF30_nlo_as115 and NNPDF30_nlo_as121, with \(\alpha _{\mathrm{S}}(m_{Z})=0.115\) and \(\alpha _{\mathrm{S}}(m_{Z})=0.121\) respectively, for each generator, for the central value of the top mass, i.e. 172.5 GeV. The number of events for each generated sample, together with an indicative computational time, are reported in Table 1.
4 Anatomy of the reconstructed top mass distribution at NLO+PS
In this section we investigate the impact of individual ingredients in a typical NLO+PS calculation on the kinematic distribution of the reconstructed top mass \(m_{Wb_j}\). On the perturbative side, we examine the impact of the different level of accuracy in the treatment of top production and decay provided by the three generators we are considering, and the impact of parton-shower effects. On the non-perturbative side, we illustrate the effect of including hadronization and underlying event in the simulation.
4.1 Les Houches event level comparison of the generators
We begin by comparing the three generators at the Les Houches event (LHE) level.
\({d\sigma }/{d m_{Wb_j}}\) distribution at LO (blue) and at NLO (red) obtained with the \(hvq\) generator, normalized to 1 in the displayed range. In the bottom panel the ratio with the LO prediction is shown
\({d\sigma }/{d m_{Wb_j}}\) distribution at LO (blue) and at NLO (red) obtained with the \(b\bar{b}4\ell \) generator, normalized to 1 in the displayed range. In the bottom panel the ratio with the LO prediction is shown
In Figs. 1 and 2 we compare \(m_{Wb_j}\), normalized to 1 in the displayed range, at LO and NLO accuracy using the \(hvq\) and the \(b\bar{b}4\ell \) generators respectively. The \(hvq\) generator includes NLO corrections only in the production process. Thus the \(m_{Wb_j}\) distributions at LO and NLO are very similar. On the other hand, in the case of the \(b\bar{b}4\ell \) generator (Fig. 2), we observe large differences below the peak region. These differences are easily interpreted as due to radiation outside the \(b\)-jet cone in the top-decay process.
The \(t\bar{t}dec\) generator allows us to specify whether NLO accuracy is required both in production and decay (default behaviour), or just in production (by using the nlowhich 1 option). In Fig. 3 we compare the two options. We see that our previous observation is confirmed: the impact of NLO corrections in production leads to a roughly constant K-factor, while the radiation from top decay affects the shape of the distribution below the peak region.
\({d\sigma }/{d m_{Wb_j}}\) distribution with NLO accuracy in production and decay (red), only in production (green) and with LO accuracy (blue) obtained with the \(t\bar{t}dec\) generator, normalized to 1 in the displayed range. In the bottom panel the ratio with the LO prediction is shown
A remaining important difference between the \(hvq\) and the other two generators has to do with the way the distribution of the top virtuality is modeled. The \(b\bar{b}4\ell \) and \(t\bar{t}dec\) generators are guaranteed to yield the correct virtuality distribution at the NLO and LO level, respectively. This is not the case for the \(hvq\) generator, where the resonance structure is recovered by a reweighting procedure that does not guarantee LO accuracy.
\({d\sigma }/{d m_{Wb_j}}\) distribution at LO obtained with \(b\bar{b}4\ell \) (red), \(t\bar{t}dec\) (blue) and \(hvq\) (green), normalized to 1 in the displayed range. In the bottom panel the ratio with the \(b\bar{b}4\ell \) prediction is shown
This is illustrated in Fig. 4, where we see that a non-negligible (although not dramatic) difference in shape is present also at the LO level between the \(hvq\) and the other two generators.
4.2 Shower effects
We now examine how the shower, i.e. the radiation beyond the hardest one, affects our distributions. First of all, we anticipate an important effect in \(hvq\), since in this case radiation in decay is fully generated by the shower. We thus expect a raise of the low mass tail in the \(m_{Wb_j}\) distribution, comparable in size to the one observed in the \(b\bar{b}4\ell \) and \(t\bar{t}dec\) generators at the LHE level. Conversely, in the \(b\bar{b}4\ell \) and \(t\bar{t}dec\) cases, we expect smaller shower corrections, since the hardest radiation in decay is already included at the LHE level.
\({d\sigma }/{d m_{Wb_j}}\) distribution obtained with \(hvq\) (upper pane) and \(b\bar{b}4\ell \) (lower pane) at the NLO LHE level (green), and at NLO+shower (in red Pythia8.2 and in blue Herwig7.1), normalized to 1 in the displayed range. In the bottom panel the ratio with the NLO LHE is shown
This is illustrated in Fig. 5, where we clearly see that in the \(hvq\) case there is an important increase of the cross section below the peak. On the other hand, in the \(b\bar{b}4\ell \) case this increase is minor or even absent, depending upon which shower program is used. In both cases, we see an enhancement in the region above the peak. This is attributed to shower radiation that is captured by the \(b\)-jet cone. We observe that, after shower, the \(hvq\) result becomes qualitatively very similar to the \(b\bar{b}4\ell \) one, as shown in Fig. 6.
\({d\sigma }/{d m_{Wb_j}}\) distribution, normalized to 1 in the displayed range, obtained with \(b\bar{b}4\ell \) (red) and \(hvq\) (blue) at the NLO+PS level using Pythia8.2
The inclusion of the shower in \(t\bar{t}dec\) leads to effects similar to those observed in \(b\bar{b}4\ell \).
4.3 Hadronization and underlying events
In Fig. 7 we show the effect of hadronization and multi-parton interactions (MPI), as modeled by Pythia8.2 and Herwig7.1, when interfaced to the \(hvq\) generator. We can see the large effect of the hadronization on the final distribution. This effect is also considerably different between Pythia8.2 and Herwig7.1. There are two main features that emerge in these plots. First of all, as expected, the MPI raise the tail of the distributions above the peak. In fact, MPI-generated particles are deposited in the \(b\)-jet cone, thus increasing the \(b\)-jet energy. Hadronization widens the peak for both generators. However, in the Pythia8.2 case, we also observe a clear enhancement of the low mass region, that is not as evident in the Herwig7.1 case. In the combined effect of hadronization and MPI, Herwig7.1 has a wider peak. On the other hand, the high tail enhancement seems similar in the two generators.
\({d\sigma }/{d m_{Wb_j}}\) distribution obtained with \(hvq\) interfaced with Pythia8.2 (upper panel) and Herwig7.1 (lower panel). In green, the NLO+PS results; in red, hadronization effects are included; in blue, NLO+PS with multi-parton interactions (MPI); and in black, with hadronization and MPI effects. The curves are normalized using the NLO+PS cross section in the displayed range
We remark that the different mechanisms that lead to an increased cross section above and below the top peak depend on the jet radius parameter R. By increasing (or decreasing) R, the peak position is shifted to the left (or right). Furthermore, differences in the implementation of radiation from the resonances, the hadronization model and the underlying events can also shift the peak, leading eventually to a displacement of the extracted top mass, that should be carefully assessed.
5 Methodology
In the following sections we will examine various sources of theoretical errors in the top-mass extraction, focusing upon three classes of observables: the reconstructed mass peak, the peak of the \(b\)-jet energy spectrum [34], and the leptonic observables of Ref. [35].
The reconstructed mass observable bears a nearly direct relation with the top mass. If two generators with the same \(m_{t}\) input parameter yield a reconstructed mass peak position that differ by a certain amount, we can be sure that if they are used to extract the top mass they will yield results that differ by roughly the same amount in the opposite direction. Of course, this is not the case for other observables. In general, for an observable O sensitive to the top mass, we will have
where \(m_{t}\) is the input mass parameter in the generator, and \(m_{t,\, c}=172.5\) GeV is our reference central value for the top mass. \(O_c\) and B differ for different generators or generator setups. Given an experimental result for O, \(O_{\mathrm{exp}}\), the extracted mass value is
By changing the generator setup, \(O_{\mathrm{c}}\) and B will assume the values \(O_{\mathrm{c}}'\) and \(B'\), and will yield a different extracted mass \(m'_t\). We will thus have
The second term is parametrically smaller, of one order higher in the deviation between the two generators, if we assume that at least one of them yields a \(m_{t}\) value sufficiently close to \(m_{t,\, c}\). We thus have
In practice, in the following, we will compute the B parameter using the \(hvq\) generator, that is the fastest one. We also checked that using the other generators for this purpose yields results that differ by at most 10%.
6 Reconstructed top mass distribution \(\varvec{m_{Wb_j}}\)
The peak of the reconstructed mass \(m_{Wb_j}\), defined in Sect. 3.1, is a representative of all the direct measurement methods. Our simplifying assumptions, that the b jets are unambiguously identified and the neutrinos are fully reconstructed, including their sign, lead to an ideal resolution on the top peak that is not realistic. We thus compute these distributions also introducing a smearing that mimics the experimental systematics. This very crude approach allows us to concentrate more on theoretical issues rather then experimental ones. For example, if by using two different generators (or the same generator with different settings) we find differences in the extracted mass using our ideal \(m_{Wb_j}\) observable, we would be forced to conclude that there is an irreducible theoretical error (i.e. an error that cannot be reduced by increasing the experimental accuracy) on the mass measurement. The same problem in case of the smeared distribution should instead be considered less severe, since the corresponding error may be reduced if the experimental resolution is improved.
We remark that also “irreducible” errors (according to the definition given above) may in fact be reduced in practice. This is the case if one of the generators at hand does not fit satisfactorily measurable distributions related to top production. As an example, a generator may not fit reasonably the profile of the b jet, and we may be forced to change the allowed range for the parameters that control it, possibly reducing the error.
In the following, we will compare our three generators interfaced to Pythia8.2, and consider scale variation effects and PDF dependence. In order to investigate the sensitivity to the intensity of radiation from the b quark, we also consider different values of \(\alpha _{\mathrm{S}}\) as input. We will then investigate the Herwig7.1 and Pythia8.2 differences.Footnote 9
It is quite obvious that the coefficient B of Eq. (8) should be very near 1 for the \(m_{Wb_j}\) observable. The values for the B coefficients that we have obtained with the three generators showered with Pythia8.2, by a linear fit of the \(m_{t}\) dependence of the \(m_{Wb_j}\) distribution, are collected in Table 2, and confirm our expectation.
6.1 Comparison among the different NLO+PS generators
We begin by showing comparisons of our three generators, interfaced with Pythia8.2, for our reference top-mass value of 172.5 GeV.
\({d\sigma }/{d m_{Wb_j}}\) distribution obtained with the \(b\bar{b}4\ell \) and \(t\bar{t}dec\) generators interfaced with Pythia8.2, for \(m_{t}=172.5\) GeV
We show in Fig. 8 the \(m_{Wb_j}\) distribution for the \(b\bar{b}4\ell \) and \(t\bar{t}dec\) generators. We see that the two generators yield a very similar shape. We have extracted the position of the maximum by fitting the distribution with a skewed Lorentzian function of the form
The peak \(m_{Wb_j}^{\max }\) is defined by
The fitting procedure is described in “Appendix B”.
As we can see from Fig. 8, the \(b\bar{b}4\ell \) and \(t\bar{t}dec\) results are very close to each other. We take this as an indication that interference effects in radiation and other off-shell effects, that are included in \(b\bar{b}4\ell \) but not in \(t\bar{t}dec\), have a very minor impact on the peak position, at least if we consider a measurement with an ideal resolution.
In order to mimic experimental resolution effects, we smear our distribution with a Gaussian of width \(\sigma =15\) GeV (that is the typical experimental resolution on the reconstructed top mass)
where \(\mathscr {N}\) is a normalization constant.
Smeared \({d\sigma }/{d m_{Wb_j}}\) distribution obtained with the \(b\bar{b}4\ell \) and \(t\bar{t}dec\) generators interfaced with Pythia8.2, for \(m_{t}=172.5\) GeV
The results, obtained with the same fitting procedure, are shown in Fig. 9. Smearing effects are such that more importance is given to the region away from the peak, where there are larger differences between the two generators, leading to a difference in the peak position of \( 140\) MeV.
\({d\sigma }/{d m_{Wb_j}}\) distribution obtained with the \(b\bar{b}4\ell \) and \(hvq\) generators interfaced with Pythia8.2, for \(m_{t}=172.5\) GeV
In Figs. 10 and 11, we compare the \(b\bar{b}4\ell \) and the \(hvq\) generators in the non-smeared and smeared case respectively. We see a negligible difference in the peak position in the non-smeared case, while, in the smeared case, the \(hvq\) generator differs from \(b\bar{b}4\ell \) by \(-147\) MeV, similar in magnitude to the case of \(t\bar{t}dec\), but with opposite sign. These findings are summarized in Table 3, where we also include results obtained at the shower level.
Smeared \({d\sigma }/{d m_{Wb_j}}\) distribution obtained with the \(b\bar{b}4\ell \) and \(hvq\) generators interfaced with Pythia8.2, for \(m_{t}=172.5\) GeV
We notice that \(hvq\), in spite of the fact that it does not implement NLO corrections in top decay, yields results and distributions that are quite close to those of the most accurate \(b\bar{b}4\ell \) generator. This is due to the fact that Pythia8.2 includes matrix-element corrections (MEC) in top decay by default, and MEC are equivalent, up to an irrelevant normalization factor, to next-to-leading order corrections in decay. This observation is confirmed by examining, in Table 4, the impact of the MEC setting on our predictions. When MEC are switched off, we see a considerable shift, near 1 GeV, in the \(hvq\) result for the peak position in the smeared distribution, and a very minor one in the \(b\bar{b}4\ell \) and \(t\bar{t}dec\) generators, that include the hardest emission off b quarks. Thus, we conclude that the MEC in Pythia8.2 do a decent job in simulating top decay as far as the \(m_{Wb_j}\) distribution is concerned. The remaining uncertainty of roughly \( 140\) MeV in the case of both \(hvq\) and \(t\bar{t}dec\) generators, pulling in opposite directions, is likely due to the approximate treatment of off-shell effects.
6.1.1 Renormalization- and factorization-scale dependence
In this section, we study the dependence of our results on the renormalization and factorization scales (\(\mu _{\mathrm {R}}\) and \(\mu _{\mathrm {F}}\)), that gives an indication of the size of higher-orders corrections. We varied \(\mu _{\mathrm {R}}\) and \(\mu _{\mathrm {F}}\) around the central scale \(\mu \) defined in Eqs. (3) and (5) according to
where \((K_{\mathrm {R}},K_{\mathrm {F}})\) are varied over the following combinations
We take \(K_{\mathrm {R}}=K_{\mathrm {F}}=1\) as our central prediction. We find that for \(b\bar{b}4\ell \) there is a non-negligible scale dependence, that in the smeared case yields a theoretical uncertainty of \({}^{+ 86}_{- 53}\) MeV. For \(t\bar{t}dec\) and \(hvq\) this uncertainty is smaller than \( 7\) MeV. This is due to the fact that, in the last two generators, the NLO corrections are performed for on-shell tops, and the top width is subsequently generated with a smearing procedure. Thus, NLO corrections remain constant around the top peak, leading to a constant scale dependence. This leads to an underestimate of scale uncertainties in \(t\bar{t}dec\) and \(hvq\).
6.1.2 PDF set dependence
We evaluated the dependence from the PDFs by considering the central member of the following PDF sets:
-
MSTW2008nlo68cl (\(\alpha _{\mathrm{S}}(m_{Z})=0.120179\)) (default) [63],
-
PDF4LHC15_nlo_30_pdfas (\(\alpha _{\mathrm{S}}(m_{Z})=0.118\)) [66] ,
-
CT14nlo (\(\alpha _{\mathrm{S}}(m_{Z})=0.118\)) [67] ,
-
MMHT2014nlo68cl (\(\alpha _{\mathrm{S}}(m_{Z})=0.120\)) [68] ,
-
NNPDF30_nlo_as_0118 (\(\alpha _{\mathrm{S}}(m_{Z})=0.118\)) [69] .
We generated the events by using the MSTW2008nlo68cl set, and obtained all other predictions using the internal reweighting facility of the POWHEG BOX. We find that the corresponding differences in the \(m_{Wb_j}\) peak position are typically below \( 9\) MeV and the variations are very similar for all the NLO+PS generators.
We also generated a sample using the central parton-distribution function of the PDF4LHC15_nlo_30_pdfas set, and, by reweighting, all its members, within the \(hvq\) generator. In this case, our error is given by the sum in quadrature of all deviations. We get a variation of \( 3\) MeV in the non-smeared case, and \( 5\) MeV for the smeared distribution. We find that the variation band obtained in this way contains the central value results for the different PDF sets that we have considered. It thus makes sense to use this procedure for the estimate of PDF uncertainties. On the other hand, reweighting for the 30 members of the set in the \(b\bar{b}4\ell \) case is quite time consuming, since the virtual corrections are recomputed for each weight. We thus assume that the PDF uncertainties computed in the \(hvq\) case are also valid for the \(b\bar{b}4\ell \) and \(t\bar{t}dec\) cases, since the dependence on the PDF is mostly due to the implementation of the production processes, and all our generators describe it at NLO accuracy, and since we have previously observed that by reweighting to several PDF sets we get very similar variations for all generators.
In general, PDF uncertainties are rather small. This is probably due to the fact that, in order to shift the position of the peak, some differences must be present in the modeling of final-state radiation (FSR). These differences may arise from differences in \(\alpha _{\mathrm{S}}\). However, reweighting in POWHEG only affects the inclusive cross section, and not the radiation, and thus final-state radiation is not modified by these changes.
6.1.3 Strong-coupling dependence
In POWHEG BOX the scale used to generate the emissions is the transverse momentum of the radiation (with respect to the emitter). At the moment, facilities to study uncertainties due to variations of this scheme are not available. On the other hand, these uncertainties would lead to a different radiation pattern around the b jet, that can in turn have a non-negligible effect on the reconstructed mass.
The simplest way at our disposal for studying the sensitivity of the reconstructed mass to the intensity of radiation from the b quark is by varying the value of \(\alpha _{\mathrm{S}}\). To this end we use the NNPDF30_nlo_as115 and NNPDF30_nlo_as121 sets, where \(\alpha _{\mathrm{S}}(m_{Z})\)=0.115 and \(\alpha _{\mathrm{S}}(m_{Z})\)=0.121, respectively. As stated earlier, we cannot use the POWHEG reweighting facility in order to study this effect, and thus we generated two dedicated samples (see Table 1).
We found that the extracted peak positions in the smeared \(m_{Wb_j}\) distributions for the two extreme values of \(\alpha _{\mathrm{S}}\) differ by \( 128\) MeV for the \(b\bar{b}4\ell \) generator, by \( 108\) MeV for the \(t\bar{t}dec\) generator and by \( 18\) MeV for \(hvq\). The small \(\alpha _{\mathrm{S}}\)-sensitivity in the \(hvq\) case is expected, since, in this case, radiation in decays is handled by the shower, and thus should be studied by varying shower parameters. In the \(b\bar{b}4\ell \) and \(t\bar{t}dec\) case, the variation is very similar, since they both include NLO radiation in decay, and the direction of the variation is as expected, i.e. the peak position is larger for the smaller \(\alpha _{\mathrm{S}}\) value, due to the reduced loss of energy outside the jet cone. Differences in the case of non-smeared distributions are in all cases not larger than \( 8\) MeV.
We can estimate the typical scale of radiation in top decay as being of the order of 30 GeV, i.e. one-half of the typical b energy in the top rest frame. The ratio of the upper to lower \(\alpha _{\mathrm{S}}(m_{Z})\) values that we have considered is 1.052, and it becomes 1.06 at a scale of 30 GeV. On the other hand, a scale variation of a factor of two above and below 30 GeV yields a variation in \(\alpha _{\mathrm{S}}\) of about 26%. This can be taken as a rough indication that a standard scale variation would yield to a variation in the peak position that is more than a factor four larger than the one obtained by varying \(\alpha _{\mathrm{S}}\).
6.1.4 Matching uncertainties
The FSREmission veto procedure (i.e. implementation 1 of Sect. 2.1.2) represents the most accurate way to perform the vetoed shower on the POWHEG BOX generated events, because it uses the POWHEG definition of transverse momentum rather than the Pythia8.2 one. The ScaleResonance procedure (i.e. method 2) introduces a mismatch (see Sect. 2.1.2) that we take as an indication of the size of the matching uncertainties. The extracted peak position for the \(b\bar{b}4\ell \) and \(t\bar{t}dec\) with the two matching procedures are summarized in Table 5.
We can see that these differences are roughly 20 MeV in \(b\bar{b}4\ell \) for both the no-smearing and smearing case, and in \(t\bar{t}dec\) they are a few MeV for the no-smearing case, and 20 MeV with smearing. When using the generic veto method of Sect. 2.1.1 we find differences of comparable size.
6.1.5 Summary of scale, PDF and \(\varvec{\alpha _{\mathrm{S}}}\) variations
In Table 6 we summarize the uncertainties due to scale, PDF and strong-coupling variations, connected with the extraction of the \(m_{Wb_j}\) peak position, for the input mass \(m_{t}=172.5\) GeV, for all the generators showered with Pythia8.2.
The upper (lower) error due to scale variation reported in the table is obtained by taking the maximum (minimum) position of the \(m_{Wb_j}\) peak for each of the seven scales choices of Eq. (16), minus the one obtained for the central scale.
In the PDF case, as discussed in Sect. 6.1.2, we compute the PDF uncertainties only for the \(hvq\) generator, and assume that they are the same for \(b\bar{b}4\ell \) and \(t\bar{t}dec\).
We consider a symmetrized strong-coupling dependence uncertainty, whose expression is given by
We stress that these variations have only an indicative meaning. In a realistic analysis, experimental constraints may reduce these uncertainties. We also stress that these are not the only theoretical uncertainties. Others may be obtained by varying Monte Carlo parameters. Here we focus specifically on those uncertainties that are associated with the NLO+PS generators.
As we have already discussed, the use of the \(hvq\) and the \(t\bar{t}dec\) generators would lead to a negligible bias in the \(m_{Wb_j}\) distribution if we were able to measure it without any resolution effects. However, if we introduce a smearing to mimic them, the description of the region away from the peak plays an important role, and the \(hvq\) and \(t\bar{t}dec\) generators yield predictions for the mass peak position that are shifted by roughly \( 140\) MeV in the downward and upward direction respectively with respect to \(b\bar{b}4\ell \).
We also notice that the \(b\bar{b}4\ell \) generator is the most affected by theoretical uncertainties. In particular, the \(t\bar{t}dec\) and \(hvq\) generators have an unrealistically small scale dependence of the peak shape, due to the way in which off-shell effects are approximately described. The \(t\bar{t}dec\) generator displays a non-negligible sensitivity only to the strong-coupling constant. The theoretical errors that we have studied here lead to very small effects for the \(hvq\) generator, since it does not include radiative corrections in the top decay. On the other hand, the \(hvq\) generator is bound to be more sensitive to variation of parameters in Pythia8.2, that in this case fully controls the radiation from the b quark.
6.1.6 Radius dependence
In this section we investigate the stability of the previous results with respect to the choice of the jet radius. The results are summarized in Table 7.
For the distributions without smearing, the differences between the three generators are small and decrease as R increases. For the smeared distributions, the differences between \(t\bar{t}dec\) and \(b\bar{b}4\ell \) decrease as the radius increases, while the difference between the \(hvq\) and the \(b\bar{b}4\ell \) generator increases.
The small differences in R dependence among the three generators in the non-smeared case can be understood if we consider that differences in the b radiation do not affect much the peak position in the non-smeared distribution, but rather they affect the strength of the tail on the left side of the peak. On the other hand, the peak position is affected by radiation in production and by the underlying-event structure, that is very similar in the three generators.
It should be noticed that the difference between the displacements of the \(t\bar{t}dec\) and \(hvq\) with respect to \(b\bar{b}4\ell \) is less than \( 55\) MeV and \( 34\) MeV, respectively, below the current statistical precision of top-mass measurements. Thus, the good agreement found among the three generators persists also for different R values.
6.2 Comparison with Herwig7.1
In order to assess uncertainties due to the showering program, in this section we compare the results obtained using Herwig7.1 and Pythia8.2.
In Table 8 we compare the \(m_{Wb_j}\) peak position extracted for the input mass \(m_{t}= 172.5\) GeV using the three generators showered with Pythia8.2 and Herwig7.1. For the \(hvq\) generator, the differences are of the order of \( 240\) MeV for both the smeared and non-smeared cases, but with opposite signs. In the smeared case, both the \(t\bar{t}dec\) and \(b\bar{b}4\ell \) generators yield much larger differences, of more than 1 GeV.
In Table 9 we report the differences between the Herwig7.1 and Pythia8.2 predictions for all the generators, at the NLO+PS level and at the full hadron level. We notice that at the NLO+PS level and without smearing, the differences between the two parton-shower programs are negligible. For the smeared distributions, at both the NLO+PS and full level, the differences are roughly 1 GeV for the \(b\bar{b}4\ell \) and the \(t\bar{t}dec\) generator. For \(hvq\) the differences are considerably smaller, although not quite negligible. Furthermore, accidental compensation effects seem to emerge in this case if we compare the peak displacement in the distributions with and without smearing.
\({d\sigma }/{d m_{Wb_j}}\) distribution obtained by showering the \(b\bar{b}4\ell \) results with Pythia8.2 and Herwig7.1, at parton-shower level (left) and with hadronization and underlying events (right)
The origin of these large differences are better understood by looking at the differential cross sections plotted in Figs. 12 and 13. In Fig. 12 we plot the results for the non-smeared case, at the NLO+PS level (left) and at the full hadron level (right): while the peak position is nearly the same for both Pythia8.2 and Herwig7.1, the shape of the curves is very different around the peak, leading to a different mass peak position when smearing is applied, as displayed in Fig. 13. We notice that in this last case we see a difference in shape also after smearing. This suggests that at least one of the two generators may not describe the data fairly.
Since we observe such large differences in the value of \(m_{Wb_j}^{\max }\) in Herwig7.1 and Pythia8.2, we have also studied whether sizeable differences are also present in the \(m_{Wb_j}^{\max }\) dependence upon the jet radius R. The results are shown in Table 10, and displayed in Fig. 14.
In the case of the \(b\bar{b}4\ell \) generator, the difference between Pythia8.2 and Herwig7.1 goes from \( 830\) to \( 1267\) MeV. Thus, assuming for instance that Pythia8.2 fits the data perfectly, i.e. that it extracts the same value of the mass by fitting the \(m_{Wb_j}^{\max }\) values obtained with the three different values of R, Herwig7.1 would extract at \(R=0.6\) a mass value that is larger by \( 437\) MeV from the one extracted at \(R=0.4\). We stress that the differences in the R behaviour of \(m_{Wb_j}^{\max }\) may have the same origin as the difference in the reconstructed mass value, since both effects may be related to the amount of energy that enters the jet cone, and it is not unlikely that, by tuning one of the two generators in such a way that they both have the same R dependence, their difference in \(m_{Wb_j}^{\max }\) would also be reduced.Footnote 10 It is unlikely, however that this would lead to a much improved agreement, since the difference in slope is much less pronounced than the difference in absolute value.
6.2.1 Alternative matching prescriptions in Herwig7.1
We have examined several variations in the Herwig7.1 settings, and in the interface between POWHEG and Herwig7.1, in order to understand whether the Herwig7.1 results are reasonably stable, or depend upon our particular settings.
Smeared \({d\sigma }/{d m_{Wb_j}}\) distribution obtained by matching the \(b\bar{b}4\ell \) generator with Pythia8.2 and Herwig7.1
Differences of \(m_{Wb_j}^{\max }\) between the Pythia8.2 and the Herwig7.1 showers, for the three generators, as a function of the jet radius
6.2.2 MEC and POWHEG options in Herwig7.1
Herwig7.1 applies matrix-element corrections by default, but it also offers the possibility to switch them off. In addition, it allows to optionally replace the MEC with its internal POWHEG method, when available, to achieve NLO accuracy in top decays.Footnote 11 We have verified that, as expected, switching off the matrix-element corrections does not significantly affect the \(b\bar{b}4\ell \) and \(t\bar{t}dec\) results. In the case of the \(hvq\) generator, we can compare the default case, where MEC is on, with the cases where POWHEG replaces MEC, and with the case where neither MEC nor POWHEG is implemented. The results are shown in Table 11.
We notice that the inclusion of MEC enhances by more than 1.3 GeV the peak position of the smeared distribution. A similar result was found in Pythia8.2 (see Table 4), where the difference was slightly less than 1 GeV. The difference between the POWHEG and MEC results is much below the 1 GeV level but not negligible. This fact is hard to understand, since the POWHEG and MEC procedures should only differ by a normalization factor.
We have seen previously that the three NLO+PS generators interfaced to Pythia8.2 yield fairly consistent results for the reconstructed top mass peak. The same consistency is not found when they are interfaced to Herwig7.1. However, the best agreement is found when the internal POWHEG option for top decay is activated in Herwig7.1, as can be seen in Table 12.
The difference between the POWHEG and MEC or POWHEG Herwig7.1 results is puzzling, since they have the same formal accuracy. We will comment about this issue later on.
6.2.3 Alternative veto procedures in Herwig7.1
As discussed in Sect. 2.1.3, Herwig7.1 offers two different classes that implement the veto procedure: the ShowerVeto, our default one, and the FullShowerVeto class. The corresponding results are summarized in Table 13. For both the \(b\bar{b}4\ell \) and the \(t\bar{t}dec\) the two procedures lead to a 200 MeV difference in the peak position for the smeared distributions. The origin of such difference is not fully clear to us. In part it may be ascribed to the fact that when using the ShowerVeto class we mix two different definitions of transverse momentum (the Herwig7.1 and the POWHEG one), and in part may be due to the fact that in the FullShowerVeto class the vetoing is done on the basis of the shower structure after reshuffling has been applied. We have also checked that the generic procedure of Sect. 2.1.1, although much slower, leads to results that are statistically compatible with the FullShowerVeto method.
6.2.4 Truncated showers
It was shown in Ref. [43] that, when interfacing a POWHEG generator to an angular-ordered shower, in order to compensate for the mismatch between the angular-ordered scale and the POWHEG hardness, that is taken equal to the relative transverse momentum in radiation, one should supply appropriate truncated showers. None of our vetoing algorithms take them into account, but it turns out that Herwig7.1 provides facilities to change the settings of the initial showering scale according to the method introduced in Ref. [71], that, in our case, are equivalent to the inclusion of truncated showers (see “Appendix D”). This is done by inserting the following instructions in the Herwig7.1 input file:
The effects of these settings for the \(b\bar{b}4\ell \) and \(t\bar{t}dec\) generators are shown in Table 14.
The inclusion of the truncated shower does not introduce dramatic changes in the peak position: in fact the differences are negligible in the distributions without smearing, and are roughly \( 130\) MeV when smearing is applied. It should be noticed that these settings slightly increase the difference with respect to the results obtained with Pythia8.2.
7 The energy of the \(\varvec{b}\) jet
In Ref. [34] it was proposed to extract \(m_{t}\) using the peak of the energy spectrum of the b jet. At leading order, the b jet consists of the b quark alone, and its energy in the top rest frame, neglecting top-width effects, is fixed and given by
i.e. the spectrum is a delta function in the energy. In the laboratory frame, because of the variable boost that affects the top, the delta function is smeared into a wider distribution, but it can be shown that its peak position remains at \(E_{b_j}^{\max }\). On the basis of this observation we are led to assume that also after the inclusion of off-shell effects, radiative and non-perturbative corrections, the relation between \(E_{b_j}^{\max }\) and the top pole-mass \(m_{t}\) should be largely insensitive to production dynamics.
We performed a study of the \(E_{b_j}^{\max }\) observable along the same lines adopted for \(m_{Wb_j}\) in the previous section. If the range of variations of the top mass around a given central value \(m_{t,\, c}\) is small enough, a linear relation between \(E_{b_j}^{\max }\) and the top mass must hold, so that we can write
It was suggested in Ref. [40] that the \(E_{b_j}\) distribution \(\mathrm {d}\sigma /\mathrm {d}E_{b_j}\) is better fitted in terms of \(\log E_{b_j}\). Thus, in order to extract the peak position, we fitted the energy distribution with a fourth order polynomial
where \(x=\log E_{b_j}\).
The parameter B of Eq. (20), extracted from a linear fit of the three \(E_{b_j}^{\max }\) values corresponding to the three different values of \(m_{t}\) that we have considered (see Table 1) using the \(hvq\) generator showered by Pythia8.2, was found to be
compatible with the expected value of 0.5 from Eq. (19).Footnote 12
7.1 Comparison among different NLO+PS generators
In Fig. 15 we plot the logarithmic energy distribution for the three generators interfaced to Pythia8.2, together with their polynomial fit. The extracted \(E_{b_j}\) peaks from the \(b\bar{b}4\ell \) and the \(t\bar{t}dec\) generators are compatible within the statistical errors. On the other hand, the \(hvq\) generator yields a prediction which is roughly \( 460\) ± \( 100\) MeV smaller than the \(b\bar{b}4\ell \) one. We thus observe that the jet modeling implemented by Pythia8.2 with MEC seems to yield slightly less energetic jets. An effect going in the same direction was also observed for the \(m_{Wb_j}\) observable (see Table 6, the first column of the results with smearing), although to a smaller extent.
Logarithmic energy distribution obtained with the three generators interfaced to Pythia8.2, together with their polynomial fit, in the range displayed in the figure. The value of \(E_{b_j}^{\max }\) for each generator is also reported
In Table 15 we have collected the values of \(E_{b_j}^{\max }\) computed with MEC, and the differences between the results with and without MEC. We notice that the MEC setting has little impact in the \(b\bar{b}4\ell \) and \(t\bar{t}dec\) cases. On the other hand, in the \(hvq\) case the absence of MEC would have lead to an \(E_{b_j}^{\max }\) value about 2 GeV smaller than with MEC. We take this as another indication that the implementation of radiation in top decay using MEC leads to results that are much closer to the NLO+PS ones.
In Table 16 we summarize our results together with the scale, PDF and \(\alpha _{\mathrm{S}}\) uncertainties, that are extracted with a procedure analogous to one described for the \(m_{Wb_j}\) observable. We also report the corresponding statistical errors of our results. We see that scale and PDF variations have negligible impact on our observable, the only important change being associated with the choice of the NLO+PS generator.
We notice that our errors on scale and PDF variations are much smaller than our statistical errors. On the other hand, these variations are performed by reweighting techniques, that, because of correlations, lead to errors in the differences that are much smaller than the error on the individual term. In view of the small size of these variations, we do not attempt to perform a better estimate of their error. On the other hand, the variation of \(\alpha _{\mathrm{S}}\) does not benefit from this cancellation, and are all below the statistical uncertainties.
As previously done for \(m_{Wb_j}\), we have also investigated the dependence of the \(b\)-jet peak positions on the jet radius. The results are summarized in Table 17.
While we observe a marked change in \(E_{b_j}^{\max }\), that grows by \( 3.4\) and \( 3.3\) GeV when going from \(R=0.4\) to 0.5 and from 0.5 to 0.6 respectively, \(t\bar{t}dec\) and \(hvq\) differ by \(b\bar{b}4\ell \) by much smaller amounts. It is not clear whether such small differences could be discriminated experimentally.
According to Eqs. (11) and (22), the uncertainties that affect the value of the extracted top mass are nearly twice the uncertainties on the \(b\)-jet energy. Considering the difference for \(R=0.5\) between \(hvq\) and \(b\bar{b}4\ell \) in Table 17, we see that, by using \(hvq\) instead of \(b\bar{b}4\ell \), the extracted top mass would be roughly 900 MeV larger. This should be compared with the corresponding difference of about 150 MeV, that is shown in Table 7, for the smeared \(m_{Wb_j}\) case.
As before, we have checked the sensitivity of our result to variations in the matching procedure in Pythia8.2, by studying the difference between ScaleResonance and FSREmission options. The differences turn out to be of the order of the statistical error.
7.2 Comparison with Herwig7.1
In this section, we study the dependence of our results on the shower MC program, comparing Herwig7.1 and Pythia8.2 predictions. We extract the differences in the \(E_{b_j}^{\max }\) position for three values of the jet radius: \(R=0.4\), 0.5 and 0.6. The results are summarized in Table 18, where we also show the results at the PS-only level, and in Fig. 16.
Differences of \(E_{b_j}^{\max }\) between the Pythia8.2 and the Herwig7.1 showers, for the three generators, as a function of the jet radius
From Table 18 we clearly see that the \(b\bar{b}4\ell \) and the \(t\bar{t}dec\) generators display larger discrepancies. For example, for the central value \(R=0.5\), we would get \(\Delta E_{b_j}^{\max }{}\approx 2\) GeV, that roughly corresponds to \(\Delta m_{t}=-4\) GeV. In the case of the \(hvq\) generator the difference is near 1 GeV, implying that the extracted mass using \(hvq\)+Herwig7.1 would be 2 GeV bigger than the one obtained with \(hvq\)+Pythia8.2.
We find that the differences between Herwig7.1 and Pythia8.2 increases for larger jet radii. Furthermore, by looking at Fig. 16, we notice that the \(b\bar{b}4\ell \) generator displays a different R dependence, as we have already observed from Table 17. Figure 16 indicates that \(b\bar{b}4\ell \) and \(t\bar{t}dec\) are in better agreement for larger values of the jet radius. This was also observed for the peak of the \(m_{Wb_j}\) smeared distribution (Table 7).
We notice that, as in the case of the reconstructed mass peak, the predominant contribution to the difference arises at the parton shower level.
As for the previous cases, we have examined the variations due to a different choice of the matching scheme in Herwig7.1, that we found to be below the 200 MeV level, and thus negligible in the present context.
8 Leptonic observables
In this section, we investigate the extraction of the top mass from the leptonic observables introduced in Ref. [35]. This method has been recently studied by the ATLAS collaboration in Ref. [72].
Following Ref. [35], we consider the subsequent five observables
i.e. the transverse momentum of the positive charged lepton, and the transverse momentum, the invariant mass, the energy and the scalar sum of the transverse momenta of the lepton pair. We compute the average value of the first three Mellin moments for each of the above mentioned observables, \(\langle (O_i)^j\rangle \), with \(i=1,\dots ,5\) and \(j=1,2,3\). We assume that, if we do not vary too much the range of the top mass, we can write the linear relation
For ease of notation, we will refer to \(O_{\mathrm{c}}^{(ij)}\) and \(B^{(ij)}\) as \(O_{\mathrm{c}}\) and B in the following. Their determination will be discussed later.
We choose as reference sample the one generated with \(b\bar{b}4\ell \) matched with Pythia8.2, using \(m_{t,\, c}=172.5\) GeV as input mass and the central choices for the PDF and scales. We indicate the values of the observables computed with this generator as \({O}^{b\bar{b}4\ell }\), and with \(O_{\mathrm{c}}'\) the values of the observable computed either with an alternative generator or with different generator settings, but using as input parameter the same reference mass. The mass value that we would extract from the events of the reference sample using the new generator is then given by
8.1 Comparison among NLO+PS generators
We begin by showing in Tables 19 and 20 the average values of the leptonic observables computed with our three NLO+PS generators interfaced with Pythia8.2 and Herwig7.1. We show the central values, the differences with respect to \(b\bar{b}4\ell \), and the upper and lower results induced by scale, PDF and \(\alpha _{\mathrm{S}}\) variations.
The scale and PDF variations are performed by reweighting. As a consequence of that, the associated error is much smaller than the statistical error on the cross section. In order to estimate it, we have divided our sample of events in ten sub-samples, computed the observables for each sub-sample, and carried out a straightforward statistical analysis on the ten sets of results. We found errors that never exceed the quoted value by more than 13%.
For the PDF variation, we have verified that differences due to variations in our reference PDF sets (see Sect. 6.1.2) are very similar among the different generators. On the other hand, a full error study using the PDF4LHC15_nlo_30_pdfas set was only performed with the \(hvq\) generator, and the associated errors exceed by far the variation band that we obtain with our reference sets. Thus, also in this case we quote the PDF variations only for \(hvq\), implying that a very similar variation should also be present for the others. It is clear from the tables that the PDF uncertainties are dominant for several observables, and scale variations are also sizeable.
The large variations in the \(\alpha _{\mathrm{S}}\) column are not always conclusive because of the large statistical errors (in parentheses), due to the fact that we cannot perform this variation by reweighting. However, unlike for the \(m_{Wb_j}\) case, here the PDF dependence is not small, and thus we cannot conclude that the \(\alpha _{\mathrm{S}}\) variation probes mainly the sensitivity to the intensity of radiation in decay, since when we vary \(\alpha _{\mathrm{S}}\) we change also the PDF set.
It is instead useful to look at the effect of MEC on the leptonic observables, displayed in Table 21.
We observe that in the \(b\bar{b}4\ell \) and \(t\bar{t}dec\) case the effect of MEC is compatible with the statistical uncertainty. In the \(hvq\) case we find instead sizeable effects. This is expected, since large-angle radiation from the b quark, by subtracting energy to the whole Wb system, affects significantly also leptonic observables.
In Ref. [35] it was observed that the observables \(p_{T} (\ell ^+\ell ^-)\) and \(m(\ell ^+\ell ^-)\) had larger errors due to a stronger sensitivity to radiative corrections, and were more sensitive to spin-correlation effects. We see a confirmation of this observations in their larger errors due to scale variation, and in the fact that for \(hvq\) their central value is shifted with respect to the \(b\bar{b}4\ell \) and \(t\bar{t}dec\) generators, that treat spin correlations in a better way.
In Table 22 we show the extracted values of the B coefficients for the first Mellin moment of each observable. The B values corresponding to the different generators are compatible within the statistical errors. We thus choose the values computed with the \(hvq\) generator, that have the smallest error. According to Eq. (24), we can translate a variation in an observable into a variation of the extracted mass, that for the first Mellin moment is simply obtained applying a \(-1/B\) factor. The results are illustrated in Table 23.
The errors shown have been obtained by summing in quadrature the statistical error and the scale and PDF uncertainties. We have not included the \(\alpha _{\mathrm{S}}\) variation in the error in order to avoid overcounting, since, in the present case, is likely to be largely dominated by the change in the associated PDF.
The overall errors on the last two lines of Table 23 are obtained with the same procedure adopted in Ref. [35] to account for correlations among the different observables. We do not see excessive differences among our three generators showered with the same Monte Carlo generator, while the differences between the Pythia8.2 and Herwig7.1 results are considerably large. This is also the case for the \(hvq\) generator, that has a much simpler interface to both Pythia8.2 and Herwig7.1.
As we did for \(m_{Wb_j}^{\max }\) and \(E_{b_j}^{\max }\), also in the present case we have computed the leptonic observables without including hadronization effects, i.e. at parton-shower only level, in order to determine whether the differences between Pythia8.2 and Herwig7.1 are due to the shower or to the hadronization. Our findings are summarized in Table 24.
Most of the differences already arise at the shower level. We also remark that, within the same SMC generator, they are not large, yielding differences in the extracted top mass of the same size as the statistical errors.
We observe in Table 23 that the inclusion of higher moments of the leptonic observables does not modify appreciably the results from the first moments. This is a consequence of the large error on the higher moments, and of the strong correlations among different moments.
The results in Table 23 are also summarized in Fig. 17, where the discrepancy between Pythia8.2 and Herwig7.1 and the mutual consistency of the different observables can be immediately appreciated.
As for the previous observables, we have studied the effect of changing the matching scheme, by switching between our two alternative matching schemes with Pythia8.2 and Herwig7.1, and by considering the settings of Eq. (18) in Herwig7.1. In both cases we find results that are consistent within statistical errors.
9 Summary
In this work we have compared generators of increasing accuracy for the production and decay of \(t\bar{t}\) pairs considering observables suitable for the measurement of the top mass. The generators that we have considered are:
-
The \(hvq\) generator [48], that implements NLO corrections in production for on-shell top quarks, and includes finite-width effects and spin correlations only in an approximate way, by smearing the on-shell kinematics with Breit-Wigner forms of appropriate width, and by generating the angular distribution of the decay products according to the associated tree-level matrix elements [57].
-
The \(t\bar{t}dec\) generator [46], that implements NLO corrections in production and decay in the narrow-width approximation. Spin correlations are included at NLO accuracy. Finite width effects are implemented by reweighting the NLO results using the tree-level matrix elements for the associated Born-level process, including however all finite width non-resonant and interference effects at the Born level for the given final state.
-
The \(b\bar{b}4\ell \) generator [47], that uses the full matrix elements for the production of the given final state, including all non-resonant diagrams and interference effects. This includes interference of QCD radiation in production and decay.
Extracted mass for the three generators matched with Pythia8.2 (red) and Herwig7.1 (blue) using the first three Mellin moments of the five leptonic observables. The horizontal band represents the weighted average of the results, and the black horizontal line corresponds to \(m_{t}=172.5\) GeV, which is the top mass value used in the \(b\bar{b}4\ell \)+Pythia8.2 reference sample
The main focus of our work has been the study of the mass distribution of a particle-level reconstructed top, consisting of a lepton-neutrino pair and a b-quark jet with the appropriate flavour. The peak position of the mass of this system is our observable, that is loosely related to the top mass. We considered its distributions both at the particle level, and by assuming that experimental inaccuracies can be summarized by a simple smearing with a resolution function, a Gaussian with a width of 15 GeV, which is the typical resolution achieved on the top mass by the LHC collaborations. This observable is an oversimplified version of the mass observables that are used in direct top-mass measurements, that are the methods that lead to the most precise mass determinations.
We have found a very consistent picture in the comparison of our three generators when they are interfaced to Pythia8.2, and thus we begin by summarizing our results for this case. We first recall what we expect from such comparison. When comparing the \(hvq\) and the \(t\bar{t}dec\) generators, we should remember that the latter has certainly better accuracy in the description of spin correlations, since it implements them correctly both at the leading and at the NLO level. However, we do not expect spin correlations to play an important role in the reconstructed top mass. As a further point, the \(t\bar{t}dec\) generator implements NLO corrections in decay. In the \(hvq\) generator, the decay is handled by the shower, where, by default, Pythia8.2 includes matrix-element corrections (MEC). These differ formally from a full NLO correction only by a normalization factor, that amounts to the NLO correction to the top width. Thus, as long as the MEC are switched on, we do not expect large differences between \(hvq\) and \(t\bar{t}dec\). As far as the comparison between \(t\bar{t}dec\) and \(b\bar{b}4\ell \), we expect the difference to be given by NLO off-shell effects, and by interference of radiation in production and decay, since these effects are not implemented in \(t\bar{t}dec\). This comparison is particularly interesting, since the interference between production and decay can be considered as a “perturbative precursor” of colour reconnection effects.
The results of these comparisons can be summarized as follows:
-
The \(t\bar{t}dec\) and the \(b\bar{b}4\ell \) generators yield very similar results for most of the observables that we have considered, implying that NLO off-shell effects and interference between production and decay are modest.
-
As far as \(m_{Wb_j}^{\max }\) (the peak of the reconstructed mass distribution) is concerned, the \(t\bar{t}dec\) and the \(hvq\) generators yield very similar results, confirming the fact that the MEC implementation in Pythia8.2 has an effect very similar to the POWHEG implementation of NLO corrections in decay in the \(t\bar{t}dec\). We have also observed that, if we switch off the MEC, the agreement between the two generators is spoiled. More quantitatively, we find that the spread in the peak of the reconstructed mass at the particle level among the three NLO+PS generators is never above 30 MeV. On the other hand, if resolution effects are accounted for with our smearing procedure, we find that the \(hvq\) result is 147 MeV smaller, and the \(t\bar{t}dec\) result 140 MeV larger than the \(b\bar{b}4\ell \) one. These values are safely below currently quoted errors for the top-mass measurements with direct methods.
If we switch off the MEC in Pythia8.2, we find that the peak position at the particle level in the \(hvq\) case is displaced by 61 MeV, while, if smearing effects are included, the shift is of 916 MeV, a rather large value, that can however be disregarded as being due to the poor accuracy of the collinear approximation in b radiation when MEC corrections are off.
-
The jet-energy peak seems to be more sensitive to the modeling of radiation from the b quark. In fact, while the \(t\bar{t}dec\) and the \(b\bar{b}4\ell \) results are quite consistent with each other, with the peak positions differing by less than 200 MeV, the \(hvq\) result differs from them by more than 500 MeV. This would correspond to a difference in the extracted mass of the top quark roughly equal to twice that amount. On the other hand, if the MEC in \(hvq\) are switched off, the shift in the b-jet energy peak is more than 1.9 GeV. This leads us to conclude that the impact of modeling of b radiation on the b-jet peak is much stronger than in the reconstructed top mass peak. We stress, however, that the difference between \(hvq\) (with MEC on) and the other two generators is safely below the errors quoted in current measurements [40].
-
For the leptonic observables, we generally see a reasonable agreement between the different generators. The largest differences are found in the \(hvq\) case, for the \(p_{T} (\ell ^+\ell ^-)\) and \(m(\ell ^+\ell ^-)\), larger than 500 MeV with respect to the other two. In Ref. [35] it was noticed that these observables had larger errors due to a stronger sensitivity to radiative corrections, and to spin-correlation effects, that are modelled incorrectly by \(hvq\).
Several sources of possible uncertainties have been explored in order to check the reliability of these conclusions. First of all, two different matching procedures for interfacing the \(t\bar{t}dec\) and \(b\bar{b}4\ell \) generators to Pythia8.2 have been implemented. For example, for the reconstructed mass peak, we have checked that switching between them leads to differences below 20 MeV for both generators. The effect of scales, \(\alpha _s\) and PDF uncertainties have also been examined, and were found to yield very modest variations in the reconstructed mass peak. It was found, in particular, that scale variations lead to a negligible peak displacement (below 7 MeV) in the \(t\bar{t}dec\) and \(hvq\) case, while the effect is of \({}^{+86}_{-53}\) MeV for \(b\bar{b}4\ell \). The lack of scale dependence in the \(hvq\) and \(t\bar{t}dec\) is easily understood as being due to the fact that the peak shape is obtained by smearing an on-shell distribution with a Breit-Wigner form, that does not depend upon any scale, and it suggests that, in order to get realistic scale-variation errors, the most accurate \(b\bar{b}4\ell \) generator should be used. We have also computed results at the shower level, excluding the effects of hadronization and multi-parton interactions, in order to see if the consistent picture found at the hadron level is also supported by the parton-level results, and we have found that this is indeed the case.
We have thus seen that the overall picture of the comparison of our three NLO+PS generators within the framework of the Pythia8.2 shower is quite simple and consistent. For the most precise observable, i.e. the peak of the reconstructed mass distribution, it leads to the conclusions that the use of the most accurate generator may lead to a shift in the measured mass of at most 150 MeV, which is well below the present uncertainties quoted by the experimental collaborations.
Our study with Herwig7.1 instead reveals several problems. We can summarize our findings as follows:
-
The results obtained with Herwig7.1 differ substantially from those obtained with Pythia8.2. In particular, the peak of the reconstructed mass distribution at the particle level is shifted by − 66 and − 39 MeV in the \(b\bar{b}4\ell \) and \(t\bar{t}dec\) cases, and by \(+\) 235 MeV in the \(hvq\) case. When the experimental resolution is accounted for, using our smearing procedure, the shift raises to −1091 and −1179 MeV in the \(b\bar{b}4\ell \) and \(t\bar{t}dec\) cases, and to − 251 MeV in the \(hvq\) case.
-
The results obtained within the Herwig7.1 framework display large differences between the \(hvq\) generator with respect to \(b\bar{b}4\ell \) and \(t\bar{t}dec\) ones. In particular, while the \(t\bar{t}dec\) result exceeds the \(b\bar{b}4\ell \) one only by about 50 MeV in both the particle level and smeared cases, \(hvq\) exceeds \(b\bar{b}4\ell \) by 311 MeV at particle level, and by 693 MeV after smearing.
These results are quite alarming. The shifts reach values that are considerably larger than current experimental uncertainties.
In the \(hvq\) case, which is the NLO+PS generator currently used for top-mass studies by the experimental collaborations, the difference in the mass-peak position between Herwig7.1 and Pythia8.2, for the smeared distribution, is − 251 MeV, uncomfortably large but still below current errors. One would then be tempted to conclude that the large shifts may be linked to some problems concerning the new generators. However, we also notice that the same difference is +235 MeV when no smearing is applied, so it is about as large in magnitude but with the opposite sign. This indicates that the shape of the reconstructed mass distribution is considerably different in the two shower models. Lastly, if we use the internal POWHEG implementation of top decay (rather than the MEC) in Herwig7.1, the difference with respect to Pythia8.2 raises to 607 MeV. Thus, we conclude that in the \(hvq\) case the smaller difference between Herwig7.1 and Pythia8.2 is accidental, and is subject to considerable variations depending upon the settings.
Also in this case we checked whether the MEC yield an improved agreement between the \(hvq\) and the other two generators, as was observed for Pythia8.2. We find that, by switching off MEC, the \(hvq\)+Herwig7.1 result decreases by 307 MeV at particle level, and by 1371 MeV in the smeared case. These effects are qualitatively similar to what was observed in Pythia8.2. However, in the present case, when MEC are switched off, the \(hvq\) result exceeds the \(b\bar{b}4\ell \) one by a negligible amount at the particle level, and is lower than the \(b\bar{b}4\ell \) one by 678 MeV in the smeared case.
The discrepancy between \(hvq\) and the other two generators is mitigated if, instead of the MEC procedure, the internal POWHEG option of Herwig7.1 for top decay is used. In this case, the discrepancy between \(hvq\) and \(b\bar{b}4\ell \) is reduced to 244 MeV with no smearing, and to 337 MeV with smearing. We thus see that the consistency of the three NLO+PS generators interfaced to Herwig7.1 is not optimal as in Pythia8.2. It is however acceptable if the internal POWHEG feature is used rather than MEC in Herwig7.1.
We have performed several studies to determine the origin of the difference between Pythia8.2 and Herwig7.1, and to check whether it could be attributed to some problem in our matching procedure. They can be summarized as follows:
-
We have shown that the difference is mostly due to the shower model, since it is already largely present at the parton level.
-
We have considered the R dependence of the Herwig7.1 result. It differs from the one in Pythia8.2, leading to the hope that both generators may not represent the same set of data well, and tuning them may reduce their differences. However, we have also noticed that the difference in slope is much smaller than the difference in size.
-
We have already mentioned that we have also compared results by making use of the internal POWHEG implementation of top decay in Herwig7.1, rather than using MEC. We have found non-negligible differences in this case.
-
We have implemented alternative veto procedure in the matching of Herwig7.1 with the NLO+PS generators. We found differences of the order of 200 MeV, not large enough to cover the discrepancy with Pythia8.2.
-
When interfacing POWHEG generators to angular-ordered showers, in order to maintain the double-logarithmic accuracy of the shower, one should introduce the so called “truncated showers” [43]. One could then worry that the lack of truncated showers is at the origin of the discrepancies that we found. Fortunately, Herwig7.1 offers some optional settings that are equivalent to the introduction of truncated showers. We found that these options lead to a shift of only 200 MeV in the peak position.
In summary, we found no indication that the discrepancy with Pythia8.2 is due to the specific matching procedure and general settings that we have used in Herwig7.1.
When comparing Herwig7.1 and Pythia8.2 in the computation of the b-jet energy peak, we have found even larger differences: when using \(b\bar{b}4\ell \) and \(t\bar{t}dec\), the shifts are of the order of 2 GeV, while for \(hvq\) the shift is around 1 GeV. They correspond to differences in the extracted mass of around 4 GeV in the first two cases, and 2 GeV in the last one. This is not surprising, in view of the stronger sensitivity of the b-jet peak to the shower model.
Finally, when considering leptonic observables, we find again large differences between Herwig7.1 and Pythia8.2. Most differences already arise at the shower level. Notice that this is in contrast with the naive view that leptonic observables should be less dependent upon QCD radiation effects and jet modeling. The comparison between Herwig7.1 and Pythia8.2 for leptonic observables can by appreciated by looking at Fig. 17, representing the value of the extracted top mass from a sample generated with \(b\bar{b}4\ell \) interfaced to Pythia8.2.
10 Conclusions
We focus our conclusions on the results obtained for the reconstructed mass peak, since the issues that we have found there apply to the direct top mass measurements, that are the most precise. The experimental collaborations extensively use the \(hvq\) generator for this kind of analyses, and since new generators of higher accuracy, the \(t\bar{t}dec\) and the \(b\bar{b}4\ell \) ones, have become available, we have addressed the question of whether the physics effects not included in \(hvq\) may lead to inaccuracies in the top-mass determination. The answer to this question is quite simple and clear when our generators are interfaced to Pythia8.2. The differences that we find are large enough to justify the use of the most accurate generators, but not large enough to drastically overturn the conclusions of current measurements. Notice that, since the \(hvq\) generator does not include NLO corrections in decays, we might have expected a very different modeling of the b-jet in \(hvq\) with respect to the other two generators, leading to important shifts in the extracted top mass value. It turns out, however, that the Pythia8.2 handling of top decay in \(hvq\), improved with the matrix-element corrections, does in practice achieve NLO accuracy up to an irrelevant normalization factor.
This nicely consistent picture does not hold anymore if we use Herwig7.1 as shower generator. In particular, it seems that the MEC implemented in Herwig7.1 do not have the same effect as the handling of radiation in decay of our modern NLO+PS generators, leading to values of the extracted top mass that can differ up to about 700 MeV. Furthermore, interfacing our most accurate NLO+PS generator (the \(b\bar{b}4\ell \) one) to Herwig7.1 leads to an extracted top mass of up to 1.2 GeV smaller with respect to the corresponding result with Pythia8.2.
At this point we have two options:
-
Dismiss the Herwig7.1 results, on the ground that its MEC handling of top decay does not match our modern generators.
-
Consider the Herwig7.1 result as a variation to be included as theoretical error.
We believe that the first option is not soundly motivated. In fact, the implementation of MEC in Pythia8.2 is also technically very close to what POWHEG does. The hardest radiation is essentially generated in the same way, and in both cases the subsequent radiation is generated with a lower transverse momentum. Thus the good agreement between the two is not surprising. The case of Herwig7.1 is completely different, since in angular-ordered showers the hardest radiation is not necessarily the first [73]. It is thus quite possible that the differences we found when Herwig7.1 handles the decay with MEC, with respect to the case when POWHEG does, are due to the fact that the two procedures, although formally equivalent (i.e. both leading to NLO accuracy) are technically different. In this last case, their difference should be attributed to uncontrolled higher-order effects, and should thus be considered as a theoretical uncertainty.
A further question that this work raises is whether we should consider the variation between the Pythia8.2 and the Herwig7.1 programs as an error that should be added to current top-mass measurements. By doing so, current errors, that are of the order of 500-600 MeV, would become larger than 1 GeV. We believe that our crude modeling of the measurement process does not allow us to draw this conclusion. The analysis procedures used in direct measurements are much more complex, and involve adequate tuning of the MC parameters and jet-energy calibration using hadronic W decays in the same top events. It is not unlikely that these procedures could lead to an increased consistency between the Pythia8.2 and Herwig7.1 results. However, in view of what we have found in our study, it is difficult to trust the theoretical errors currently given in the top quark mass determination if alternative NLO+PS and shower generators combinations are not considered.
Notes
This is also the case for a top-mass determination based upon the spectrum of \(\gamma \gamma \) production near the \(t\bar{t}\) threshold [24], that however is likely to be statistically limited, even at the high luminosity LHC.
For a recent discussion of all these issues see Ref. [14].
The \(hvq\) and \(t\bar{t}dec\) generators can be found under the User-Processes-V2 directory of the POWHEG BOX V2 repository in the hvq and ttb_NLO_dec directories, respectively. The \(b\bar{b}4\ell \) generator can be found under the User-Processes-RES/b_bbar_4l directory of the POWHEG BOX RES code. Detailed instructions are found at powhegbox.mib.infn.it.
An interesting example of work along this direction can be found in Refs. [52, 53], where the impact of the colour reconnection model on top-mass measurement is analyzed. In Ref. [54], a study is performed to determine whether the use of jet-grooming techniques in top-mass measurement can reduce the Monte Carlo tune dependence.
A related approach within the MC@NLO framework has been presented in Ref. [60].
By non-resonant we mean processes that do not contain an intermediate top quark, e.g. \(pp \rightarrow b\,\bar{b} \,Z\rightarrow b\,\bar{b} \,W^+\, W^- \rightarrow b\, \bar{b}\,e^+\nu _{e}\, \mu ^-\bar{\nu }_{\mu }\).
Note that this notation is the opposite of what is commonly adopted for B mesons, where B refers to the meson containing the \(\bar{b}\) quark.
Unless specified otherwise, Pythia8.2 and Herwig7.1 are setup to run in full hadron mode including shower, hadronization and multi-parton interactions.
Similarly, one could fit appropriate calibration observables associated to the b-jet structure, along the lines of Ref. [70].
These options are activated by the instructions set ShowerHandler:HardEmission None or set ShowerHandler:HardEmission POWHEG, respectively.
When using the \(b\bar{b}4\ell \) generator we obtain \(B= 0.54\pm 0.07\), while with the \(t\bar{t}dec\) one, we get \(B= 0.50\pm 0.03\). When using Herwig7.1 instead of Pythia8.2, we find values compatible with the given ones within 10%.
We used an hdamp value equal to the input top-quark mass, i.e. the qmass parameter for the \(hvq\) generator, tmass for \(b\bar{b}4\ell \) and \(t\bar{t}dec\).
This behaviour may be changed in the future.
A simple example is also illustrated in Sect. 7.2 of Ref. [43].
References
Particle Data Group collaboration, C. Patrignani et al., Electroweak model and constraints on new physics, review of particle physics. Chin. Phys. C 40, 100001 (2016)
Gfitter Group collaboration, M. Baak, J. Cúth, J. Haller, A. Hoecker, R. Kogler, K. Mönig et al., The global electroweak fit at NNLO and prospects for the LHC and ILC. Phys. J. C 74, 3046 (2014). arXiv:1407.3792
ATLAS, CDF, CMS, D0 collaboration, First combination of Tevatron and LHC measurements of the top-quark mass. arXiv:1403.4427
ATLAS collaboration, M. Aaboud et al., Measurement of the top quark mass in the \(t\bar{t}\rightarrow \) dilepton channel from \(\sqrt{s}=8\) TeV ATLAS data. Phys. Lett. B 761, 350–371 (2016). arXiv:1606.02179
CMS collaboration, V. Khachatryan et al., Measurement of the top quark mass using proton-proton data at \({\sqrt{s}}\) = 7 and 8 TeV. Phys. Rev. D 93, 072004 (2016). arXiv:1509.04044
CMS collaboration, Measurement of the top quark mass with lepton+jets final states in pp collisions at \(\sqrt{s}=13~\text{TeV}\), Tech. Rep. CMS-PAS-TOP-17-007, CERN, Geneva (2017)
ATLAS collaboration, Measurement of the top quark mass in the \(t\bar{t}\rightarrow \) lepton+jets channel from \(\sqrt{s}=8 \,\text{ TeV }\), ATLAS data. Tech. Rep. ATLAS-CONF-2017-071, CERN, Geneva (2017)
B. Pearson, Top quark mass in ATLAS, in 10th International Workshop on Top Quark Physics (TOP2017) Braga (Portugal, 2017). arXiv:1711.09763
CMS collaboration, A. Castro, Recent Top Quark Mass Measurements from CMS, in 10th International Workshop on Top Quark Physics (TOP2017) (Braga, 2017). arXiv:1712.01027
G. Degrassi, S. Di Vita, J. Elias-Miro, J.R. Espinosa, G.F. Giudice, G. Isidori et al., Higgs mass and vacuum stability in the Standard Model at NNLO. JHEP 08, 098 (2012). arXiv:1205.6497
D. Buttazzo, G. Degrassi, P.P. Giardino, G.F. Giudice, F. Sala, A. Salvio et al., Investigating the near-criticality of the Higgs boson. JHEP 12, 089 (2013). arXiv:1307.3536
A. Andreassen, W. Frost, M.D. Schwartz, Scale invariant instantons and the complete lifetime of the standard model. Phys. Rev. D 97, 056006 (2018). arXiv:1707.08124
S. Chigusa, T. Moroi, Y. Shoji, State-of-the-art calculation of the decay rate of electroweak vacuum in the standard model. Phys. Rev. Lett. 119, 211801 (2017). arXiv:1707.09301
P. Nason, The Top Mass in Hadronic Collisions. arXiv:1712.02796
A.H. Hoang, The Top Mass: Interpretation and Theoretical Uncertainties, in Proceedings, 7th International Workshop on Top Quark Physics (TOP2014) (Cannes, 2014). arXiv:1412.3649
I.I.Y. Bigi, M.A. Shifman, N.G. Uraltsev, A.I. Vainshtein, The pole mass of the heavy quark. Perturbation theory and beyond. Phys. Rev. D 50, 2234–2246 (1994). arXiv:hep-ph/9402360
M. Beneke, V.M. Braun, Heavy quark effective theory beyond perturbation theory: Renormalons, the pole mass and the residual mass term. Nucl. Phys. B 426, 301–343 (1994). arXiv:hep-ph/9402364
M. Beneke, P. Marquard, P. Nason, M. Steinhauser, On the ultimate uncertainty of the top quark pole mass. Phys. Lett. B 775, 63–70 (2017). arXiv:1605.03609
A.H. Hoang, C. Lepenik, M. Preisser, On the light massive flavor dependence of the large order asymptotic behavior and the ambiguity of the pole mass. JHEP 09, 099 (2017). arXiv:1706.08526
A. Pineda, Determination of the bottom quark mass from the Upsilon(1S) system. JHEP 06, 022 (2001). arXiv:hep-ph/0105008
G.S. Bali, C. Bauer, A. Pineda, C. Torrero, Perturbative expansion of the energy of static sources at large orders in four-dimensional SU(3) gauge theory. Phys. Rev. D 87, 094517 (2013). arXiv:1303.3279
M. Beneke, Y. Kiyo, P. Marquard, A. Penin, J. Piclum, M. Steinhauser, Next-to-next-to-next-to-leading order QCD prediction for the top antitop \(S\)-wave pair production cross section near threshold in \(e^+e^-\) annihilation. Phys. Rev. Lett. 115, 192001 (2015). arXiv:1506.06864
F. Simon, A First Look at the Impact of NNNLO Theory Uncertainties on Top Mass Measurements at the ILC, in Proceedings, International Workshop on Future Linear Colliders (LCWS15) (Whistler, 2016). arXiv:1603.04764
S. Kawabata, H. Yokoya, Top-quark mass from the diphoton mass spectrum. Phys. J. C 77, 323 (2017). arXiv:1607.00990
M. Czakon, P. Fiedler, A. Mitov, Total top-quark pair-production cross section at Hadron colliders through \(O(\alpha _{{\rm S}}^4)\). Phys. Rev. Lett. 110, 252004 (2013). arXiv:1303.6254
CMS collaboration, V. Khachatryan et al., Measurement of the t-tbar production cross section in the e-mu channel in proton-proton collisions at sqrt(s) = 7 and 8 TeV. JHEP 08, 029 (2016). arXiv:1603.02303
ATLAS collaboration, G. Aad et al., Measurement of the \(t\bar{t}\) production cross-section using \(e\mu \) events with b-tagged jets in pp collisions at \(\sqrt{s}\) = 7 and 8 \(\,\text{ TeV }\) with the ATLAS detector. Eur. Phys. J. C 74, 3109 (2014). arXiv:1406.5375
U. Langenfeld, S. Moch, P. Uwer, Measuring the running top-quark mass. Phys. Rev. D 80, 054009 (2009). arXiv:0906.5273
S. Alioli, P. Fernandez, J. Fuster, A. Irles, S.-O. Moch, P. Uwer et al., A new observable to measure the top-quark mass at hadron colliders. Eur. Phys. J. C 73, 2438 (2013). arXiv:1303.6415
S. Kawabata, Y. Shimizu, Y. Sumino, H. Yokoya, Weight function method for precise determination of top quark mass at Large Hadron Collider. Phys. Lett. B 741, 232–238 (2015). arXiv:1405.2395
J. Gao, C.S. Li, H.X. Zhu, Top quark decay at next-to-next-to leading order in QCD. Phys. Rev. Lett. 110, 042001 (2013). arXiv:1210.2808
M. Brucherseifer, F. Caola, K. Melnikov, \(\cal{O}(\alpha _s^2)\) corrections to fully-differential top quark decays. JHEP 04, 059 (2013). arXiv:1301.7133
A.H. Hoang, S. Mantry, A. Pathak, I.W. Stewart, Extracting a short distance top mass with light grooming. arXiv:1708.02586
K. Agashe, R. Franceschini, D. Kim, M. Schulze, Top quark mass determination from the energy peaks of b-jets and B-hadrons at NLO QCD. Eur. Phys. J. C 76, 636 (2016). arXiv:1603.03445
S. Frixione, A. Mitov, Determination of the top quark mass from leptonic observables. JHEP 09, 012 (2014). arXiv:1407.2763
CMS collaboration, A.M. Sirunyan et al., Measurement of the top quark mass in the dileptonic \(t\bar{t}\) decay channel using the mass observables \(M_{b\ell }\), \(M_{T2}\), and \(M_{b\ell \nu }\) in pp collisions at \(\sqrt{s}=8\) TeV. Phys. Rev. D 96, 032002 (2017). arXiv:1704.06142
C.G. Lester, D.J. Summers, Measuring masses of semiinvisibly decaying particles pair produced at hadron colliders. Phys. Lett. B 463, 99–103 (1999). arXiv:hep-ph/9906349
A.J. Barr, B. Gripaios, C.G. Lester, Transverse masses and kinematic constraints: from the boundary to the crease. JHEP 11, 096 (2009). arXiv:0908.3779
CMS collaboration, Determination of the normalised invariant mass distribution of \(\text{ t }\bar{\text{ t }}+\)jet and extraction of the top quark mass, Tech. Rep. CMS-PAS-TOP-13-006, CERN, Geneva (2016)
CMS collaboration, Measurement of the top-quark mass from the b jet energy spectrum, Tech. Rep. CMS-PAS-TOP-15-002, CERN, Geneva (2015)
ATLAS collaboration, G. Aad et al., Determination of the top-quark pole mass using \( t\overline{t} \) + 1-jet events collected with the ATLAS experiment in 7 TeV pp collisions 10, 121 (2015). arXiv:1507.01769
ATLAS collaboration, M. Aaboud et al., Measurement of lepton differential distributions and the top quark mass in \(t\bar{t}\) production in \(pp\) collisions at \(\sqrt{s}=8\) TeV with the ATLAS detector. Eur. Phys. J. C 77, 804 (2017). arXiv:1709.09407
P. Nason, A New method for combining NLO QCD with shower Monte Carlo algorithms. JHEP 11, 040 (2004). arXiv:hep-ph/0409146
S. Frixione, P. Nason, C. Oleari, Matching NLO QCD computations with Parton Shower simulations: the POWHEG method. JHEP 11, 070 (2007). arXiv:0709.2092
S. Alioli, P. Nason, C. Oleari, E. Re, A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX. JHEP 06, 043 (2010). arXiv:1002.2581
J.M. Campbell, R.K. Ellis, P. Nason, E. Re, Top-pair production and decay at NLO matched with parton showers. JHEP 04, 114 (2015). arXiv:1412.1828
T. Ježo, J.M. Lindert, P. Nason, C. Oleari, S. Pozzorini, An NLO+PS generator for \({{t \bar{t}}}\) and \({{W t}}\) production and decay including non-resonant and interference effects. Eur. Phys. J. C 76, 691 (2016). arXiv:1607.04538
S. Frixione, P. Nason, G. Ridolfi, A Positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction. JHEP 09, 126 (2007). arXiv:0707.3088
T. Sjöstrand, S. Ask, J.R. Christiansen, R. Corke, N. Desai, P. Ilten et al., An Introduction to PYTHIA 8.2. Comput. Phys. Commun. 191, 159–177 (2015). arXiv:1410.3012
M. Bahr et al., Herwig++ Physics and manual. Eur. Phys. J. C 58, 639–707 (2008). https://doi.org/10.1140/epjc/s10052-008-0798-9. arXiv:0803.0883
J. Bellm et al., Herwig 7.0/Herwig++ 3.0 release note. Eur. Phys. J. C 76, 196 (2016). https://doi.org/10.1140/epjc/s10052-016-4018-8. arXiv:1512.01178
D. Wicke, P.Z. Skands, Non-perturbative QCD Effects and the Top Mass at the Tevatron. Nuovo Cim. B 123, S1 (2008). arXiv:0807.3248
T. Sjöstrand, Colour reconnection and its effects on precise measurements at the LHC (2013). arXiv:1310.8073
A. Andreassen, M.D. Schwartz, Reducing the top quark mass uncertainty with jet grooming. JHEP 10, 151 (2017). arXiv:1705.07135
G. Heinrich, A. Maier, R. Nisius, J. Schlenk, M. Schulze, L. Scyboz et al., NLO and off-shell effects in top quark mass determinations. arXiv:1709.08615
G. Bevilacqua, H.B. Hartanto, M. Kraus, M. Schulze, M. Worek, Top quark mass studies with \( t\overline{t}j \) at the LHC. JHEP 03, 169 (2018). arXiv:1710.07515
S. Frixione, E. Laenen, P. Motylinski, B.R. Webber, Angular correlations of lepton pairs from vector boson and top quark decays in Monte Carlo simulations. JHEP 04, 081 (2007). arXiv:hep-ph/0702198
E. Boos et al., Generic user process interface for event generators, in Physics at TeV colliders. Proceedings, Euro Summer School (Les Houches 2001). arXiv:hep-ph/0109068
T. Ježo, P. Nason, On the treatment of resonances in next-to-leading order calculations matched to a parton shower. JHEP 12, 065 (2015). arXiv:1509.09071
R. Frederix, S. Frixione, A.S. Papanastasiou, S. Prestel, P. Torrielli, Off-shell single-top production at NLO matched to parton showers. JHEP 06, 027 (2016). arXiv:1603.01178
F. Cascioli, P. Maierhofer, S. Pozzorini, Scattering amplitudes with open loops. Phys. Rev. Lett. 108, 111601 (2012). arXiv:1111.5206
A.D. Martin, W.J. Stirling, R.S. Thorne, G. Watt, Parton distributions for the LHC. Eur. Phys. J. C 63, 189–285 (2009). arXiv:0901.0002
M. Cacciari, G.P. Salam, G. Soyez, FastJet User Manual. Eur. Phys. J. C 72, 1896 (2012). [arXiv:1111.6097
M. Cacciari, G.P. Salam, G. Soyez, The Anti-k(t) jet clustering algorithm. JHEP 04, 063 (2008). arXiv:0802.1189
J. Butterworth et al., PDF4LHC recommendations for LHC Run II. J. Phys. G 43, 023001 (2016). arXiv:1510.03865
S. Dulat, T.-J. Hou, J. Gao, M. Guzzi, J. Huston, P. Nadolsky et al., New parton distribution functions from a global analysis of quantum chromodynamics. Phys. Rev. D 93, 033006 (2016). arXiv:1506.07443
L.A. Harland-Lang, A.D. Martin, P. Motylinski, R.S. Thorne, Parton distributions in the LHC era: MMHT 2014 PDFs. Eur. Phys. J. C 75, 204 (2015). arXiv:1412.3989
NNPDF collaboration, R.D. Ball et al., Parton distributions for the LHC Run II. JHEP 04, 040 (2015). arXiv:1410.8849
G. Corcella, R. Franceschini, D. Kim, Fragmentation uncertainties in hadronic observables for top-quark mass measurements. Nucl. Phys. B 929, 485–526 (2018). arXiv:1712.05801
A. Schofield, M.H. Seymour, Jet vetoing and Herwig++. JHEP 01, 078 (2012). arXiv:1103.4811
ATLAS collaboration, Measurement of lepton differential distributions and the top quark mass in \(t{\bar{t}}\) production in \(pp\) collisions at \(\sqrt{s}=8\) TeV with the ATLAS detector, Tech. Rep. ATLAS-CONF-2017-044, CERN, Geneva (2017)
M.H. Seymour, Matrix element corrections to parton shower algorithms. Comput. Phys. Commun. 90, 95–101 (1995). arXiv:hep-ph/9410414
Acknowledgements
We would like to thank Peter Richardson for important suggestions on the settings of Herwig7.1 and on our POWHEG-Herwig7.1 interfaces, and Stefan Prestel for help with the Pythia8.2 code and for suggestions on the implementation of our POWHEG-Pythia8.2 interface. We also like to thank Simon Plätzer and Stephen Webster for help and suggestions on our Herwig7.1 input files, and for illustrating us aspects of the Herwig7.1 code. Finally we thanks Roberto Franceschini, Alexander Mitov and Stefano Pozzorini for suggestions on the manuscript, and Mike Seymour, Peter Skands, Törbjorn Sjöstrand, Michelangelo Mangano, Andreas Papaefstathiou, and Andrzej Siodmok for useful discussions. We acknowledge the CINECA and the Regione Lombardia award under the LISA initiative 2016-2018, for the availability of high performance computing resources and support. C.O. wishes to thank Maurizio Cremonesi for the help in running the code on the CINECA resources, under the project LISA PWHG-RES. The research of T.J. was supported by the Swiss National Science Foundation (SNF) under contracts BSCGI0-157722 and CRSII2-160814.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: The treatment of remnants
In POWHEG it is possible to separate the real cross section, in a given singular region \(\alpha \), into two contributions
where \(R^{\alpha }_f\) does not contain any singularities, while \(R^{\alpha }_s\) is singular. Only \(R^{\alpha }_s\) is exponentiated in the Sudakov form factor and used for the computation of \(\tilde{B}\), while the leftover \(R^{\alpha }_f\), dubbed the remnant contribution, is finite upon phase space integration [43].
In all our three NLO generators it is possible to achieve this separation for initial-state radiation (ISR) emissions by setting the parameter hdampFootnote 13 in the powheg.input file. Denoting with \(\alpha _{\mathrm{ISR}}\) the production region, \(R^{\alpha _{\mathrm{ISR}}}_s\) and \(R^{\alpha _{\mathrm{ISR}}}_f\) are defined as
where \(p_{T} ^{\alpha _{\mathrm{ISR}}}\) is the transverse momentum of the emitted parton relative to the beam axis. The scalup variable contained in the Les Houches event, that is used by the parton shower program to veto emissions harder than the POWHEG one, is set equal to \(p_{T} ^{\alpha _{\mathrm{ISR}}}\).
Since remnant events are non-singular, the associated radiation has transverse momenta of the order of the partonic center-of-mass energy. We can thus define scalup as
We have checked that, by using as scalup the default POWHEG scale (i.e. the transverse momentum of the radiated parton) the \(m_{Wb_j}{}\) and the \(E_{b_j}^{\max }\) values are very close to the ones we have presented in this paper. This is consistent with the expectation that these observables should be relatively insensitive to radiation in production, that in our case is always treated as ISR. The same holds for the leptonic observable \(m(\ell ^+\ell ^-)\). For the remaining ones, a higher sensitivity to ISR effects is not excluded, and in fact the differences of the first Mellin moments reported in Table 19 with the corresponding ones obtained with the default scalup value, for the \(hvq\) generator showered with Pythia8.2, are given by
In comparison with Table 19, we see that these variations are of the same order or smaller than those arising from scale and PDF uncertainties.
In the \(b\bar{b}4\ell \) code, when ISR remnants are generated, no radiation in decay is produced.Footnote 14 Thus, in this case, radiation off the resonances is fully handled by the parton shower, without the use of a veto algorithm to limit the \(p_{T} \) of the radiated partons.
The \(t\bar{t}dec\) generator does instead implement radiation in decay also for remnants, and thus in this case vetoing is performed as for the standard events.
The absence of emissions from the t and \(\bar{t}\) resonances in remnant events for the \(b\bar{b}4\ell \) generator, in contrast with the \(t\bar{t}dec\) one, is probably the reason why the former generator displays a slightly larger sensitivity to matrix-element corrections (see Tables 4, 15 and 21).
To summarize:
-
\(hvq\): Emissions in decay are never vetoed. For remnant events the scalup value used to limit radiation in production is set to \(\sqrt{\hat{s}}/2\).
-
\(t\bar{t}dec\): Emissions in decay are always vetoed. For remnant events the scalup value is set to \(\sqrt{\hat{s}}/2\).
-
\(b\bar{b}4\ell \): Emissions in decay are always vetoed except if the event is a remnant, in which case they are never vetoed. For remnant events the scalup value is set to \(\sqrt{\hat{s}}/2\).
Appendix B: Fitting procedure
We always adopt the same fitting procedures in order to find the maximum of a distribution. Calling Y(x) the histogram of our distribution, and \(y(x,\{a\})\) our fitting functional form, where \(\{a\}\) represent the fitting parameters, we proceed as follows:
-
We find the bin with the highest value, and assign its center to the variable \(x_{\mathrm{max}}\).
-
We find all surrounding bins whose value is not less than \(Y(x_{\mathrm{max}})/2\). We assign to the variable \(\Delta \) the range covered by these bins divided by two.
-
We minimize the \(\chi ^2\) computed from the difference of the integral of \(y(x,\{a\})\) in each bin, divided by the bin size, with respect to Y(x), choosing as a range all bins that overlap with the segment \([x_{\mathrm{max}}-\Delta , x_{\mathrm{max}}+\Delta ]\).
-
From the fitted function we extract the maximum position and assign it to \(x_{\mathrm{max}}\).
-
If the reduced \(\chi ^2\) of the fit is less than 2, we keep this result. If not, we replace \(\Delta \rightarrow 0.95\times \Delta \) and repeat the operation until this condition is met.
Appendix C: PowhegHooks.h
In Pythia8.2 the transverse-momentum definition used in the veto algorithm for radiation in production is different from the POWHEG one. In order to deal with this issue, the authors of Pythia8.2 implemented a veto employing the POWHEG transverse momentum definition, by constructing a UserHooks subclass in the PowhegHooks.h file, which is currently part of the Pythia8.2 distribution.
The Pythia8.2 manual suggests to use the PowhegHooks class whenever showering a POWHEG style matched NLO+PS process. In order to implement the features of the PowhegHooks class in our generators, avoiding at the same time conflicts with the PowhegHooksBB4L one (that performs vetoing also for resonance decays), we added them to the PowhegHooksBB4L class, where they are activated by setting POWHEG:veto = 1.
All the results presented in this paper were obtained using POWHEG:veto = 0. However, we have also investigated the sensitivity of our results to this setting, by showering all our samples with POWHEG:veto = 1. The differences with respect to the POWHEG:veto = 0 setting are listed in Table 25 for all the generators under study. The shifts obtained are not large and mostly compatible among the different generators.
Appendix D: Truncated showers
We briefly remind the need for truncated showers in the specific example of a POWHEG implementation of top decay interfaced to an angular-ordered parton shower.
If top decay is treated without NLO corrections, the parton shower will generate radiation from the b quark with an unrestricted initial angle. The hardest radiation will take place along the shower after an arbitrary number of soft radiations at larger angles.
If POWHEG style NLO corrections are included, the hardest radiation, consisting in the emission of a gluon, will be generated first by POWHEG, and the parton shower will build angular-ordered jets starting from the b quark and the POWHEG gluon. The b quark will be assigned an initial angle for showering equal to \(\theta _{bg}\), the angle between the b and the POWHEG gluon. The soft radiation emitted by the b quark at angles larger than \(\theta _{bg}\) will thus be missing. In order to remedy to this problem, it was proposed in Ref. [43] to let both the b quark and the gluon radiate with initial angle \(\theta _{bg}\) and with a \(p_{T} \) veto set to the gluon relative transverse momentum, and to add a b quark \(p_{T} \) vetoed shower starting with the angle that would have been assigned if the gluon had not be radiated (i.e. an unrestricted angle), and stopping at the \(\theta _{bg}\) angle.Footnote 15
The veto technique introduced in Ref. [71], and activated in Herwig7.1 with the settings of Eq. (18), performs a fully equivalent task. In fact, with these settings, the initial angle for radiation from a gluon is taken as the maximum angle between the gluon and its two colour partners, that, in our case, leads to unrestricted radiation from the gluon, i.e. \(\theta _{gg} \lesssim 1\). However, the colour factor \(C_A\) associated with this radiation is reduced by a factor of two if \(\theta _{gg}>\theta _{bg}\), while it is restored to \(C_A\) for smaller angles. Since \(C_A/2 \approx C_F\) in the large \(N_c\) limit, we see that this is equivalent to the inclusion of a vetoed truncated shower from the b quark down to the angle \(\theta _{bg}\).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Ferrario Ravasio, S., Ježo, T., Nason, P. et al. A theoretical study of top-mass measurements at the LHC using NLO+PS generators of increasing accuracy. Eur. Phys. J. C 78, 458 (2018). https://doi.org/10.1140/epjc/s10052-018-5909-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-5909-7